Вестник отделения строительных наук РААСН 2011 №15
Подождите немного. Документ загружается.

РОССИЙСКАЯ
АКАДЕМИЯ
АРХИТЕКТУРЫ
И
СТРОИТЕЛЬНЫХ
НАУК
МОСКВА
–
ОРЕЛ
–
КУРСК
, 2011
80
_________________________________________________________________________________________________________________
Анализ
существующих
экспериментальных
данных
по
величине
R
T3
0
–
нижней
грани
-
це
трещинообразования
при
трехосном
сжатии
[1-2] –
показывает
,
что
величина
k
Т
сущест
-
венно
меньше
величины
k (k
Т
= 3,43÷5,22
при
|
σ
2
|/R
ПР
= 0,07÷0,44).
При
этом
зависимость
k
Т
от
R
ПР
и
|
σ
2
|/R
ПР
выражена
гораздо
менее
определенно
,
чем
для
k.
Это
находится
в
соответст
-
вии
с
полученными
выше
теоретическими
результатами
,
а
сами
экспериментальные
значения
k
Т
близки
к
тому
,
что
дает
выражение
(5).
Поэтому
для
практических
расчетов
целесообразно
принять
k
Т
= const,
положив
,
например
k
Т
= 3,0.
Заметим
,
что
все
рекомендации
относятся
к
случаю
отсутствия
давления
жидкости
в
порах
и
трещинах
материала
.
При
наличии
такого
давления
необходимо
вводить
дополнительный
коэффициент
α
по
методике
[4].
Выводы
1.
В
процессе
трехосного
нагружения
бетона
(
σ
1
<
σ
2
=
σ
1
)
развиваются
как
трещины
сдвига
,
так
и
трещины
отрыва
,
причем
преобладающая
роль
тех
или
других
трещин
,
а
вместе
с
тем
и
величина
k –
коэффициента
эффективности
бокового
давления
–
существенно
зави
-
сит
от
величины
бокового
давления
σ
2
и
от
проектной
марки
бетона
R
ПР
.
2.
Достижение
R
T3
0
–
нижней
границы
трещинообразования
при
трехосном
сжатии
определяется
развитием
начальных
трещин
сдвига
.
При
этом
величина
k
Т
–
коэффициента
интенсивности
бокового
давления
по
трещиностойкости
в
отличие
от
k
лишь
слабо
зависит
от
σ
2
и
R
ПР
.
3.
Для
практических
целей
рекомендуется
нормировать
величину
k
в
соответствии
с
рисунком
3,
а
величину
k
Т
принимать
равной
3,0.
Библиографический список
1.
Жиренков
,
А
.
Н
.
Особенности
разрушения
существенно
неоднородных
материалов
при
одноосном
и
объемном
сжатии
[
Текст
] /
А
.
Н
.
Жиренков
,
Н
.
В
.
Карцев
,
Р
.
О
.
Красновский
//
Вестник
гражданских
инженеров
. –
СПб
ГАСУ
, 2009. –
№
3(20) –
С
. 111-113.
2.
Жиренков
,
А
.
Н
.
Прогнозирование
прочности
существенно
неоднородных
материалов
при
объемном
сжатии
[
Текст
] /
А
.
Н
.
Жиренков
,
Н
.
В
.
Карцев
,
Р
.
О
.
Красновский
//
Вестник
гра
-
жданских
инженеров
. –
СПб
ГАСУ
, 2010. –
№
1(22). –
С
. 56-59.
3.
Панасюк
,
В
.
В
.
Предельное
равновесие
хрупких
тел
с
трещинами
[
Текст
] /
В
.
В
Пана
-
сюк
. –
Киев
:
Наукова
думка
, 1968. –
С
. 248.
4.
Мальцов
,
К
.
А
.
Прочность
бетона
при
частичном
насыщении
его
пор
водой
под
дав
-
лением
[
Текст
] /
К
.
А
.
Мальцов
,
И
.
Б
.
Соколов
//
Труды
координац
.
совещ
.
по
гидротехн
.
ВНИИ
гидротехники
им
.
Б
.
Е
.
Веденеева
, 1970. –
вып
. 58. –
С
. 199-207.
5.
Малашкин
,
Ю
.
Н
.
Исследование прочности
и
процесса
деформирования
бетона
с
учетом
вида
напряженного
состояния
[
Текст
] /
Ю
.
Н
.
Малашкин
,
В
.
Г
.
Иш
,
Б
.
В
.
Тябликов
,
И
.
М
.
Безгодов
//
Труды
координац
.
совещ
.
по
гидротехн
.
ВНИИ
гидротехники
им
.
Б
.
Е
.
Веде
-
неева
, 1975. –
вып
. 99. –
С
. 21-25.
6.
Зайцев
,
Ю
.
В
Прочность
и
долговечность
конструкционных
материалов
с
трещиной
[
Текст
] /
Ю
.
В
.
Зайцев
,
С
.
Н
.
Леонович
. –
Минск
:
БНТУ
, 2010. –
С
. 362.

РОССИЙСКАЯ
АКАДЕМИЯ
АРХИТЕКТУРЫ
И
СТРОИТЕЛЬНЫХ
НАУК
МОСКВА
–
ОРЕЛ
–
КУРСК
, 2011
_________________________________________________________________________________________________________________
81
УДК
539.3:534.1
ЗВЕРЯЕВ
Е
.
М
.
(
Московская
государственная
академия
коммунального
хозяйства
и
строительства
,
г
.
Москва
)
МАКАРОВ
Г
.
И
.
(
НИИОСП
им
.
М
.
Н
.
Герсеванова
,
г
.
Москва
)
НОВОЕ РЕШЕНИЕ ЗАДАЧИ О ПРОДОЛЬНОМ УДАРЕ
СОСРЕДОТОЧЕННОЙ СИЛОЙ ПО СТЕРЖНЮ
Классическая
теория
удара
основывается
на
предположении
о
малости
отношения
на
-
чальной
скорости
удара
к
скорости
распространения
волны
в
теле
.
Считается
,
что
частое
не
-
согласование
теоретических
и
экспериментальных
результатов
связано
с
влиянием
упро
-
щающих
предположений
,
принятых
при
теоретических
изысканиях
,
в
особенности
с
откло
-
нениями
реальных
и
теоретических
краевых
и
начальных
условий
.
В
литературе
рассматри
-
ваются
задачи
о
продольном
и
поперечном
ударе
для
стержней
без
учета
местных
деформа
-
ций
и
с
их
учетом
[1].
Полученное
на
основании
гипотезы
плоских
сечений
уравнение
дви
-
жения
элемента
стержня
при
поперечных
колебаниях
не
позволяет
установить
волновой
ха
-
рактер
движения
[1].
Трудности
решения
подобных
задач
связаны
с
тем
,
что
ударная
нагруз
-
ка
сингулярная
во
времени
и
в
случае
сосредоточенной
силы
в
пространстве
,
и
необходимо
связать
сингулярное
воздействие
с
сингулярными
бегущими
волнами
и
регулярными
коле
-
баниями
стержня
по
собственным
формам
колебаний
.
В
итоге
ряды
получаются
плохо
схо
-
дящимися
и
плохо
анализируемыми
.
С
целью
преодолевания
подобного
рода
трудности
в
настоящей
работе
приводится
пример
построения
решения
без
разложения
быстро
меняю
-
щихся
сингулярных
воздействий
и
решений
в
ряды
по
медленно
меняющимся
функциям
.
Используется
установленная
в
работе
[2]
асимптотическая
форма
представления
дельта
-
функции
.
В
этой
же
работе
без
каких
-
либо
гипотез
геометрического
и
статического
характе
-
ра
из
уравнений
теории
упругости
выделены
уравнения
движения
для
длинной
упругой
по
-
лосы
под
действием
поперечной
нагрузки
путем
отбрасывания
малых
членов
в
исходных
уравнениях
.
В
результате
исходной
задаче
поставлена
в
соответствие
близкая
(
в
асимптоти
-
ческим
смысле
)
задача
,
состоящая
из
трех
связанных
между
собой
граничными
условиями
подзадач
:
о
продольных
волновых
и
колебательных
движениях
стержня
,
о
продольно
-
поперечных
сдвиговых
волновых
и
колебательных
движениях
стержня
и
о
поперечных
коле
-
баниях
балки
.
Цель
работы
заключается
в
разработке
техники
построения
решения
в
виде
бегущих
и
стоячих
волн
и
их
взаимодействия
для
случая
продольных
движений
стержня
,
как
составляющей
общего
решения
задачи
поперечного
к
оси
полосы
ударного
воздействия
.
Размерное
уравнение
продольного
движения
элемента
стержня
длины
l
имеет
вид
[1]:
E
f
x
u
t
u
E
∗
∗
∗
∗
∗
=
∂
∂
−
∂
∂
2
2
2
2
ρ
. (1)
Здесь
∗
u
−
продольное
смещение
элемента
стержня
,
∗
x
−
его
продольная
координата
,
E,
ρ
−
удельная
плотность
и
модуль
упругости
материала
,
(
)
∗∗∗∗
= txff , −
внешняя
нагрузка
,
∗
t
−
время
.
Произведем
в
уравнении
движения
замену
переменных
по
формулам
lxx =
∗
,
luu =
∗
,
Ttt =
∗
,
в
которых
величины
t
u
x
,
,
являются
безразмерными
,
T
−
наибольший
период
про
-
дольных
колебаний
стержня
.
Уравнение
движения
после
замены
переменных
принимает
вид
:
fuu
a
=
′′
−
&&
2
1
, (2)
где
2
2
2
l
ET
a
ρ
=
,
E
lf
f
∗
=
−
безразмерная
скорость
распространения
возмущения
в
стержне
и
безраз
-
мерная
нагрузка
.
Точкой
обозначено
дифференцирование
по
времени
,
штрихом
−
по
координате
х
.
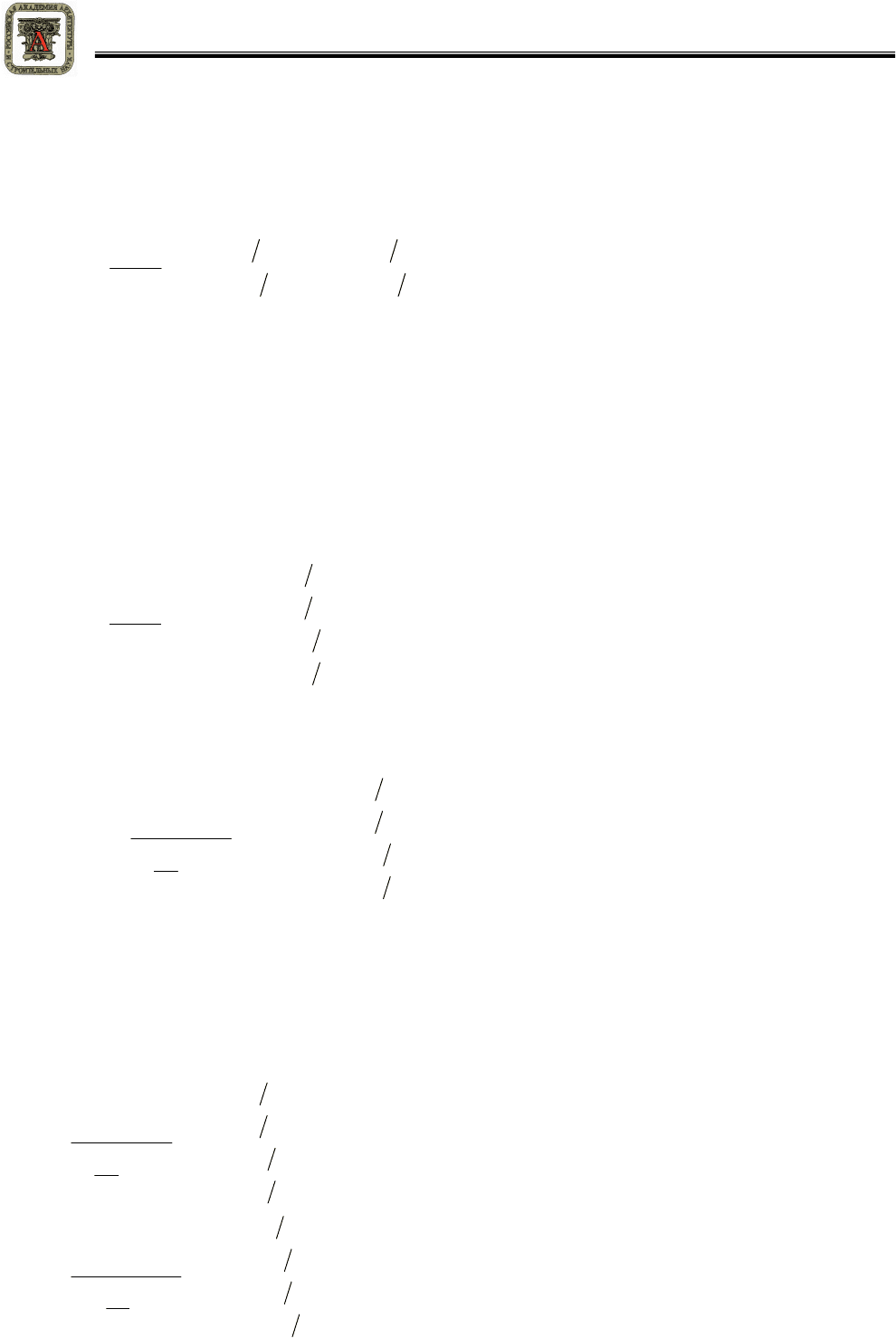
РОССИЙСКАЯ
АКАДЕМИЯ
АРХИТЕКТУРЫ
И
СТРОИТЕЛЬНЫХ
НАУК
МОСКВА
–
ОРЕЛ
–
КУРСК
, 2011
82
_________________________________________________________________________________________________________________
Решение
уравнения
(2)
будем
искать
в
виде
суммы
решений
sr
uuu +=
,
где
r
u
−
пе
-
ремещение
,
соответствующее
бегущей
волне
,
s
u
−
перемещение
,
соответствующее
стоячим
волнам
,
порожденными
отражением
бегущей
волны
от
защемления
.
Построим
решение
r
u
,
соответствующее
бегущей
волне
.
Нагрузку
зададим
в
виде
асимптотического
представления
дельта
-
функции
[2, 3]:
(
)
( )
(
)
( )
−
×
−
=
ε
ε
ε
ε
ε
tk
tk
xk
xk
kPk
f
2
2
1
1
2
21
exp
exp
exp
exp
4
.
Величины
ε
,
1
k
,
2
k
характеризуют
форму
и
скорость
приложения
нагрузки
.
Нагрузка
счи
-
тается
приложенной
в
точке
0
=
x
в
момент
времени
0
=
t
.
Верхние
строки
справедливы
при
0
<
x
и
0
<
t
,
нижние
−
при
0
>
x
и
0
>
t
.
При
0
→
ε
локальная
распределенная
вдоль
стержня
и
во
времени
нагрузка
собирается
в
точку
0
=
x
,
0
=
t
.
Т
.
е
.
имеют
место
предельные
соотношения
:
(
)
(
)
txPf
δ
δ
ε
=
→0
lim
,
∫
=
∞→
d
c
dc
Pfdx
,
lim
.
Здесь
точки
c
x
=
и
dx
=
являются
концами
стержня
.
Они
в
дальнейшем
для
определенно
-
сти
будут
считаться
жестко
защемленными
.
Выражение
для
внешней
силы
можно
переписать
следующим
образом
:
(
)
[
]
( )
[ ]
( )
[ ]
( )
[ ]
−−
+−
−
+
=
ε
ε
ε
ε
ε
tkxk
tkxk
tkxk
tkxk
kPk
f
21
21
21
21
2
21
exp
exp
exp
exp
4
при
при
при
при
0 ,0
0 ,0
0 ,0
0 ,0
>>
<>
><
<
<
tx
tx
tx
tx
. (3)
Решение
уравнения
(2)
должно
удовлетворять
начальным
условиям
:
(
)
(
)
00,0, == xuxu
rr
&
. (4)
Уравнение
(2)
при
нагрузке
(3)
имеет
частное
решение
:
( )
(
)
[
]
( )
[ ]
( )
[ ]
( )
[ ]
−−
+−
−
+
−
=
ε
ε
ε
ε
tkxk
tkxk
tkxk
tkxk
k
a
k
kPk
u
pr
21
21
21
21
2
2
2
2
1
21
exp
exp
exp
exp
4
при
при
при
при
0 ,0
0 ,0
0 ,0
0 ,0
>>
<>
><
<
<
tx
tx
tx
tx
(5)
и
общее
,
соответствующее
бегущей
волне
(
)
(
)
(
)
atxfatxfu
gr
−++=
21
. (6)
Эти
функции
должны
удовлетворять
при
0
=
t
нулевым
начальным
условиям
:
(
)
(
)
0=+
grpr
uu
,
(
)
(
)
0=+
grpr
uu
&&
,
поскольку
до
момента
удара
0
=
t
все
точки
стержня
находятся
в
покое
.
Подставив
в
начальные
условия
(4)
выражения
(5), (6),
получим
два
уравнения
отно
-
сительно
двух
неизвестных
функций
21
,
ff
:
(
)
( )
( )
( )
( ) ( )
0
exp
exp
exp
exp
4
21
1
1
1
1
2
2
2
2
1
21
=++
−
−
−
xfxf
xk
xk
xk
xk
k
a
k
kPk
ε
ε
ε
ε
при
при
при
при
0 ,0
0 ,0
0 ,0
0 ,0
+→>
−→>
+→<
−
→
<
tx
tx
tx
tx
(
)
( )
( )
( )
( ) ( )
0
exp
exp
exp
exp
4
21
1
1
1
1
2
2
2
2
1
2
1
2
=
′
−
′
+
−−
−
−
−
xfxfa
xk
xk
xk
xk
k
a
k
kPk
ε
ε
ε
ε
ε
при
при
при
при
0 ,0
0 ,0
0 ,0
0 ,0
+→>
−→>
+→<
−
→
<
tx
tx
tx
tx
После
интегрирования
второго
уравнения
по
x
получаем
уравнение
:

РОССИЙСКАЯ
АКАДЕМИЯ
АРХИТЕКТУРЫ
И
СТРОИТЕЛЬНЫХ
НАУК
МОСКВА
–
ОРЕЛ
–
КУРСК
, 2011
_________________________________________________________________________________________________________________
83
(
)
( )
( )
( )
( ) ( )
[ ]
0
exp
exp
exp
exp
4
21
1
1
1
1
2
2
2
2
1
2
2
=−+
−
−−
−
−
xfxfa
xk
xk
xk
xk
k
a
k
Pk
ε
ε
ε
ε
при
при
при
при
0 ,0
0 ,0
0 ,0
0 ,0
+→>
−→>
+→<
−
→
<
tx
tx
tx
tx
при
складывании
которого
с
первым
и
вычитая
,
определяем
вид
искомых
функций
(
)
xf
1
,
(
)
xf
2
.
Заменив
в
полученном
выражении
в
соответствии
с
формулой
(6)
в
(
)
xf
1
аргумент
x
на
at
x
+
а
в
(
)
xf
2
на
at
x
−
,
получим
функции
,
задающие
вид
бегущих
волн
:
( )
(
)
( )
( )
( )
(
)
( )
( )
( )
−
−
+
−
−−
−
−
−=
εξ
εξ
εξ
εξ
εξ
εξ
εξ
εξ
ξ
1
1
1
1
21
1
1
1
1
2
2
2
2
2
1
1
exp
exp
exp
exp
exp
exp
exp
exp
8
2
k
k
k
k
kk
k
k
k
k
a
k
k
a
k
P
f
при
при
при
при
0 ,0
0 ,0
0 ,0
0 ,0
>>
<>
><
<
<
tx
tx
tx
tx
( )
(
)
( )
( )
( )
(
)
( )
( )
( )
−
−
−
−
−−
−
−
=
εη
εη
εη
εη
εη
εη
εη
εη
η
1
1
1
1
21
1
1
1
1
2
2
2
2
2
1
2
exp
exp
exp
exp
exp
exp
exp
exp
8
2
k
k
k
k
kk
k
k
k
k
a
k
k
a
k
P
f
при
при
при
при
0 ,0
0 ,0
0 ,0
0 ,0
>>
<>
><
<
<
tx
tx
tx
tx
в
которых
для
сокращения
записи
использованы
обозначения
atx
+
=
ξ
,
at
x
−
=
η
.
Таким
образом
,
окончательное
выражение
для
бегущей
волны
при
ударе
имеет
вид
:
(
)
[
]
( )
[ ]
( )
[ ]
( )
[ ]
−−
+−
−
+
−
=
ε
ε
ε
ε
tkxk
tkxk
tkxk
tkxk
k
a
k
kPk
u
r
21
21
21
21
2
2
2
2
1
21
exp
exp
exp
exp
4
(
)
( )
( )
( )
(
)
( )
( )
( )
+
−−
−−
−
−
+
−−
−+
+
−
−
+
εξ
εξ
εξ
εξ
εξ
εξ
εξ
εξ
1
1
1
1
21
1
1
1
1
2
2
2
2
2
1
exp
exp
exp
exp
exp
exp
exp
exp
8
2
k
k
k
k
kk
k
k
k
k
a
k
k
a
k
P
(
)
( )
( )
( )
(
)
( )
( )
( )
−−
−−
−
−
+
−
−−
−
−
+
εη
εη
εη
εη
εη
εη
εη
εη
1
1
1
1
21
1
1
1
1
2
2
2
2
2
1
exp
exp
exp
exp
exp
exp
exp
exp
8
2
k
k
k
k
kk
k
k
k
k
a
k
k
a
k
P
при
при
при
при
0 ,0
0 ,0
0 ,0
0 ,0
>>
<>
><
<
<
tx
tx
tx
tx
Решение
s
u
уравнения
(2),
соответствующее
стоячим
волнам
,
должно
удовлетворять
граничным
условиям
защемления
на
концах
стержня
при
c
x
=
и
dx
=
:
0=+
sr
uu
.
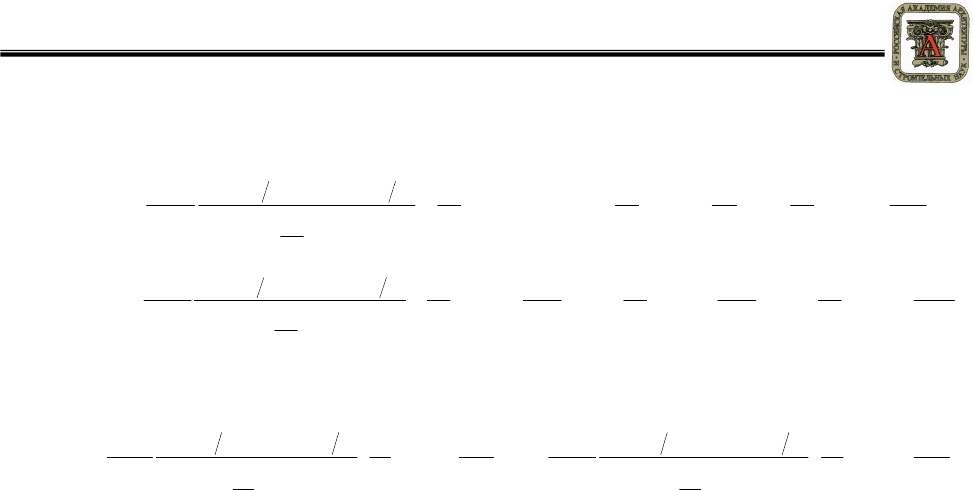
(7)
Решение
s
u
уравнения
(2)
при
нулевой
правой
части
будем
искать
в
виде
:
( ) ( )
xXtUu
n
n
n
s
∑
∞
=
=
0
, (8)
где
cnxncnxnX
n
ππππ
sincoscossin −= −
собственная
функция
,
удовлетворяющая
уравнению
:
0
22
=+
′′
nn
XnX
π
(9)
и
однородным
граничным
условиям
:
(
)
(
)
0== dXcX
nn
. (10)
Умножим
уравнение
(2)
на
n
X
и
проинтегрируем
в
пределах
от
c
до
:
0
1
2
=
″
−
∫∫
dxXudxXu
a
n
d
c
s
n
s
d
c
&&
. (11)
Преобразовав
второй
член
этого
уравнения
с
помощью
формулы
интегрирования
по
частям
,
получим
запись
:
d
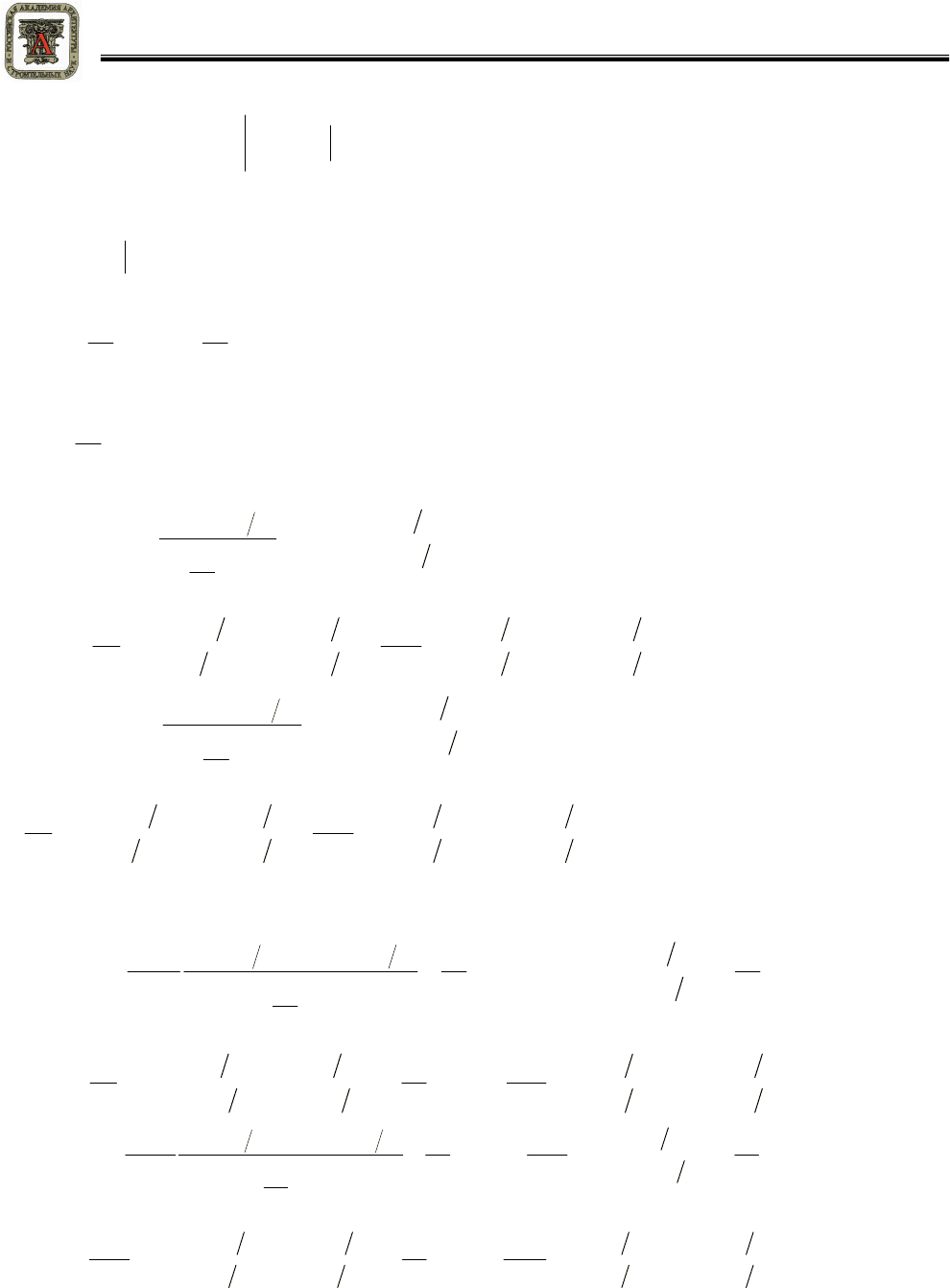
РОССИЙСКАЯ
АКАДЕМИЯ
АРХИТЕКТУРЫ
И
СТРОИТЕЛЬНЫХ
НАУК
МОСКВА
–
ОРЕЛ
–
КУРСК
, 2011
84
_________________________________________________________________________________________________________________
∫∫
′′
+
′
−
′
=
″
d
c
n
s
d
c
n
s
d
c
n
s
n
d
c
s
dxXuXuXudxXu
.
Здесь
первый
член
в
правой
части
равен
нулю
в
силу
граничных
условий
(10).
Второй
член
преобразуется
следующим
образом
:
( ) ( ) ( ) ( )
cXtcudXtduXu
n
s
nn
s
d
c
n
s
′
−
′
=
′
,,
и
,
введя
обозначение
для
первого
члена
в
уравнении
(11):
nn
s
d
c
U
a
dxXu
a
&&
&&
22
11
=
∫
,
получим
с
учетом
равенства
(7)
уравнение
для
функции
n
U
:
( ) ( ) ( ) ( ) ( ) ( )
[
]
tcutduncXtcudXtduUnU
a
rr
n
r
n
r
nn
,,2,,
1
22
2
+=
′
−
′
=+
ππ
&&
. (12)
Входящие
в
правую
часть
уравнения
величины
имеют
вид
:
( )
(
)
(
)
( )
+
−
−
=
ε
ε
ε
tk
tk
kk
k
a
k
ckP
tcu
r
2
2
21
2
2
2
2
1
1
exp
exp
4
exp
,
(
)
(
)
( ) ( )
(
)
(
)
( ) ( )
−+
−+
−
−−
−−
+
εε
εε
εε
εε
tktk
tktk
kk
tktk
tktk
a
k
11
11
21
11
11
2
expexp
expexp
2expexp
expexp
2
2
при
при
0t
0t
>
<
( )
(
)
(
)
( )
+
−
−
−
=
ε
ε
ε
tk
tk
kk
k
a
k
dkP
tdu
r
2
2
21
2
2
2
2
1
1
exp
exp
4
exp
,
(
)
(
)
( ) ( )
(
)
(
)
( ) ( )
−+
−+
−
−−
−−
+
εε
εε
εε
εε
tktk
tktk
kk
tktk
tktk
a
k
11
11
21
11
11
2
expexp
expexp
2expexp
expexp
2
2
при
при
0t
0t
>
<
Функции
p
n
U
и
p
n
U
&
,
определяющие
перемещение
и
скорость
в
выражении
(8),
соот
-
ветствующие
частому
решению
уравнения
(12),
имеют
вид
:
(
)
(
)
(
)
( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
0 tпри
0 при
expexp
expexp
2expexp
expexp
2
exp
exp
4
expexp2
11
11
21
22
2
2
1
11
11
2
22
2
2
1
2
2
21
22
2
2
2
2
2
2
2
1
11
2
2
>
<
−+
−+
+−
+−−
−−
×
×
++
−
+
−
−+
=
t
tktk
tktk
kk
n
k
tktk
tktk
a
k
n
k
tk
tk
kkn
k
k
a
k
dkck
a
Pn
U
p
n
εε
εε
π
εεε
εε
π
εε
ε
π
ε
εεπ
(
)
(
)
(
)
( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
0 tпри
0 при
expexp
expexp
2expexp
expexp
2
exp
exp
4
expexp2
11
11
2
2
1
22
2
2
1
11
11
1
2
2
22
2
2
1
2
2
2
21
22
2
2
2
2
2
2
2
1
11
2
>
<
−−
−−
+−
+−
−−−
×
×
++
−−
+
−
−+
=
t
tktk
tktk
kk
n
k
tktk
tktk
a
kk
n
k
tk
tk
kk
n
k
k
a
k
dkck
a
Pn
U
p
n
εε
εε
ε
π
εεε
εε
ε
π
εε
ε
ε
π
ε
εεπ
&
Общее
решение
g
n
U
уравнения
(12)
возьмем
в
форме
:
+
+
=
tanBtanB
tanAtanA
U
g
n
ππ
ππ
sincos
sincos
21
21
при
при
0t
0t
>
<
. (13)
При
этом
решение
g
n
p
nn
UUU +=
и
его
производная
g
n
p
nn
UUU
&&&
+=
должны
удовлетво
-
рять
условиям
непрерывности
в
точке
0
=
t
.
РОССИЙСКАЯ
АКАДЕМИЯ
АРХИТЕКТУРЫ
И
СТРОИТЕЛЬНЫХ
НАУК
МОСКВА
–
ОРЕЛ
–
КУРСК
, 2011
_________________________________________________________________________________________________________________
85
В
момент
приложения
нагрузки
(
в
момент
удара
)
0
=
t
функции
p
n
U
и
p
n
U
&
принимают
следующие
значения
:
( )
( ) ( )
+−
++
+
−
−+
=
2
2
20
0
21
1
4
expexp2
0
21
22
2
2
1
2
22
2
2
1
21
22
2
2
2
2
2
2
2
1
11
2
2
kk
n
k
a
k
n
k
kkn
k
k
a
k
dkck
a
Pn
U
p
n
π
ε
π
ε
π
ε
εεπ
( )
(
)
(
)
+−
−
++
−
+
−
−+
=
0
0
21
1
1
1
4
expexp2
0
2
2
1
22
2
2
11
2
2
22
2
2
1
2
21
22
2
2
2
2
2
2
2
1
11
2
ε
π
εε
π
εε
π
ε
εεπ
kk
n
k
a
kk
n
kkk
n
k
k
a
k
dkck
a
Pn
U
p
n
&
из
которых
видно
,
что
функция
p
n
U
в
точке
0
=
t
непрерывна
,
а
в
функции
p
n
U
&
первое
и
вто
-
рое
слагаемые
имеют
разрывы
,
третье
слагаемое
равно
нулю
.
Введем
обозначения
:
(
)
(
)
ε
π
ε
εεπ
2
21
22
2
2
2
2
2
2
2
1
11
2
1
4
expexp2 kk
n
k
k
a
k
dkck
a
Pn
b
+
−
−+
=
,
(
)
(
)
ε
π
ε
εεπ
a
kk
n
k
k
a
k
dkck
a
Pn
b
1
2
2
22
2
2
1
2
2
2
2
1
11
2
2
4
expexp2
+
−
−+
=
и
перепишем
выражение
для
скорости
в
точке
ноль
:
( ) ( )
−
−=
−
+
−
=
1
1
1
1
1
1
0
2121
bbbbU
p
n
&
при
при
0t
0t
+→
−
→
. (14)
Примем
для
решения
(13)
нулевые
начальные
условия
для
компоненты
при
0
<
t
,
оз
-
начающие
,
что
до
приложения
нагрузки
собственные
колебания
отсутствовали
.
В
соответст
-
вии
с
этим
получаем
0
21
==
AA
.
Условия
непрерывности
для
перемещения
и
скорости
в
точке
0
=
t
дают
с
учетом
соотношения
(14)
уравнения
для
определения
произволов
интег
-
рирования
1
B
,
2
B
:
1
0
B
=
,
(
)
(
)
22121
Bbbbb
+−−=−
.
Отсюда
получаем
0
1
=
B
,
(
)
211
2
bbB
−=
.
Для
искомой
функции
n
U
получаем
окончательное
выражение
:
(
)
tanbbUUU
g
n
p
nn
π
cos2
21
−++=
при
0
>
t
.
Подстановка
этого
выражения
в
формулу
(8)
дает
решение
для
стоячей
волны
при
ударе
сосредоточенной
силой
.
Заметим
,
что
в
результате
использования
аппроксимации
син
-
гулярного
нагружения
в
виде
асимптотического
представления
дельта
-
функции
,
построение
решения
сведено
к
решению
классической
задачи
распространения
волн
с
помощью
извест
-
ной
формулы
Даламбера
[4].
Локальное
возмущение
,
вызванное
ударом
,
распространяется
по
стержню
и
,
дойдя
до
края
,
порождает
стационарные
собственные
колебания
в
стержне
с
закрепленными
краями
.
Естественно
,
что
при
граничных
условиях
на
концах
стержня
проце
-
дура
построения
решения
сохраняется
.
Это
позволяет
строить
решение
при
задании
кинема
-
тического
возмущения
в
некотором
сечении
стержня
.
В
задаче
о
волновом
движении
при
по
-
перечном
ударе
к
задаче
о
продольном
движении
добавляется
рассмотрение
совместной
за
-
дачи
о
продольных
продольно
-
поперечных
сдвиговых
волновых
и
колебательных
движениях
стержня
и
о
поперечных
колебаниях
балки
,
т
.
к
.
возникают
все
три
вида
колебаний
.
Мы
пола
-
гаем
,
что
задание
кинематического
возмущения
конца
стержня
в
поперечном
направлении
будет
интересным
для
моделирования
сейсмического
воздействия
на
строительные
объекты
.
Библиографический список
1.
Пановко
,
Я
.
Г
.
Введение
в
теорию
механического
удара
[
Текст
] /
Я
.
Г
.
Пановко
. –
М
.:
Наука
,1977. – 224
с
.
2.
Зверяев
,
Е
.
М
.
Общий
метод
построения
теорий
типа
Тимошенко
[
Текст
] /
Е
.
М
.
Зверя
-
ев
,
Г
.
И
.
Макаров
//
Прикладная
математика
и
механика
, 2008. –
Т
. 72. –
Вып
. 2. –
С
. 306-321.
3.
Зверяев
,
Е
.
М
.
Анализ
гипотез
,
используемых
при
построении
теории
балок
и
пластин
[
Текст
] /
Е
.
М
.
Зверяев
//
Прикладная
математика
и
механика
, 2003. –
Т
. 67. –
Вып
. 3. –
С
. 472-481.
4.
Тихонов
,
А
.
Н
.
Уравнения
математической
физики
[
Текст
] /
А
.
Н
.
Тихонов
,
А
.
А
.
Са
-
марский
. –
М
.:
Наука
, 1966. – 724
с
.

РОССИЙСКАЯ
АКАДЕМИЯ
АРХИТЕКТУРЫ
И
СТРОИТЕЛЬНЫХ
НАУК
МОСКВА
–
ОРЕЛ
–
КУРСК
, 2011
86
_________________________________________________________________________________________________________________
УДК
624.044:534.833
ЗЫЛЕВ
В
.
Б
.
(
Московский
государственный
университет
путей
сообщения
,
г
.
Москва
)
ТЕОРЕМЫ ВЗАИМНОСТИ ДЛЯ ДИНАМИКИ
СИСТЕМ С ДЕМПФИРОВАНИЕМ
В
[1]
дается
доказательство
свойств
взаимности
для
случая
установившихся
гармони
-
ческих
колебаний
.
В
[2]
свойства
взаимности
формулируются
и
доказываются
в
общем
виде
,
но
не
даются
формулировки
конкретных
теорем
,
характерных
для
строительной
механики
,
силы
сопротивления
в
[2]
не
рассматриваются
.
Отметим
работу
[3],
где
используется
теорема
о
взаимности
перемещений
без
рассмотрения
ее
доказательства
.
В
нашей
работе
[4]
даются
формулировки
теорем
взаимности
для
идеально
упругой
системы
в
традиционной
для
строи
-
тельной
механики
форме
и
приводятся
их
доказательства
с
помощью
метода
разложения
движения
по
собственным
формам
колебаний
.
В
настоящей
работе
теоремы
взаимности
обобщаются
на
случай
учета
сил
сопротивления
.
Будем
рассматривать
линейную
систему
с
точечными
сосредоточенными
массами
.
В
отношении
сил
сопротивления
сделаем
следующие
упрощающие
допущения
.
Они
могут
быть
представлены
силами
,
пропорциональными
массам
и
скоростям
точек
,
или
получаться
путем
умножения
матрицы
демпфирования
на
составляющие
скоростей
по
соответствую
-
щим
степеням
свободы
.
Матрица
демпфирования
должна
быть
взята
пропорциональной
мат
-
рице
жесткости
системы
,
соответствующей
динамическим
степеням
свободы
.
Как
известно
[5],
при
сделанных
ограничениях
для
каждой
обобщенной
координаты
l
q
может
быть
запи
-
сано
независимое
дифференциальное
уравнение
:
l
l
lllll
M
Q
qqnq =++
2
0
2
ω
&&&
. (1)
Искомое
движение
системы
представляется
в
виде
суммы
движений
по
отдельным
,
взаимно
ортогональным
формам
собственных
колебаний
:
nn
qVqVqVZ
r
r
r
r
+++= ...
2211
. (2)
Отметим
здесь
,
что
формы
собственных
колебаний
l
V
r
–
это
те
же
формы
,
что
и
в
сис
-
теме
без
учета
сил
сопротивления
.
Теорема о взаимности перемещений. Начнем
с
приложения
мгновенных
сосредото
-
ченных
импульсов
к
системе
.
Пусть
система
получает
мгновенный
импульс
G
по
направле
-
нию
степени
свободы
с
номером
j
(
рисунок
1,
а
).
После
нанесения
импульса
система
будет
совершать
свободные
колебания
.
Уравнение
(1)
будет
в
данном
случае
однородным
и
его
частное
решение
может
иметь
вид
:
te
q
q
l
tn
l
l
l
l
ω
ω
sin
0
−
=
&
.
(3)
Здесь
22
0
lll
n−=
ωω
–
круговая
частота
с
учетом
сил
сопротивления
.
Это
решение
соответствует
некоторой
начальной
обобщенной
скорости
l
q
0
&
и
нулево
-
му
начальному
смещению
.
Определение
начальной
обобщенной
скорости
l
q
0
&
в
данном
слу
-
чае
можно
выполнить
по
известной
методике
[5],
с
использованием
свойств
ортогональности
форм
собственных
колебаний
:
РОССИЙСКАЯ
АКАДЕМИЯ
АРХИТЕКТУРЫ И СТРОИТ
МОСКВА
–
ОРЕЛ
–
КУРСК
, 2011
_____________________________________
_______________________________________________
l
q
0
&
=
)0(
l
jlj
l
iil
M
m
G
Vm
M
ZVm
i
=
∑
&
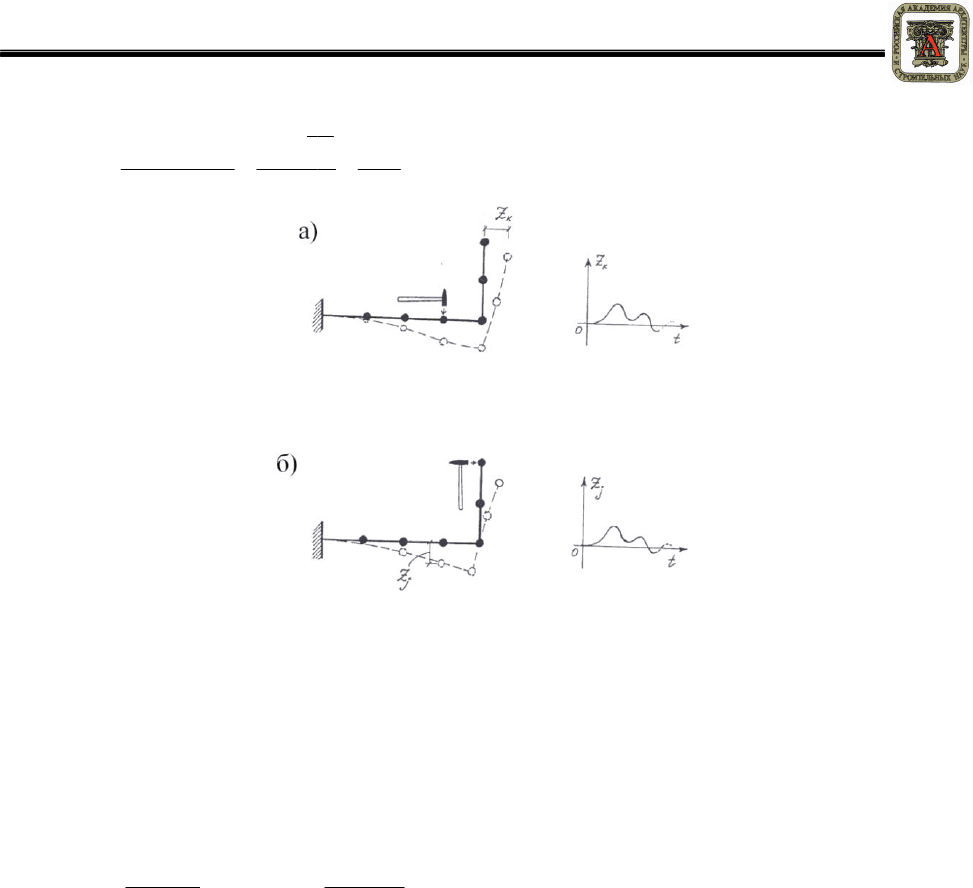
Рисунок 1 –
Нанесение мгновенного импульса по
направлении ,
замер смещения по направлению
Здесь
∑
=
2
ilil
VmM
–
обобщенная масса соответствующая обобщенной координате с
номером
l
.
Таким
образом
,
движение системы после нанесения импульса определилось
Смещение
по
координате
k
Z
будет
sin
1
11
11
1
+
=
−
te
M
VGV
Z
tnkj
k
ω
ω
Если
поменять
степени
свободы для нанесения импульса и замера перемещения см
рисунок
1,
б
)
и
решить
задачу
аналогичным образом то получим выражение тождественное
с
(
4).
Действительно
,
компоненты вектора формы собственных колебаний
формулу
(4)
совершенно
одинаково Таким обра
)()( tZtZ
jkkj
=
и
при
учете
сил
сопротивления Формула выражает теорему о взаимности перемещений
для
импульсов
.
Представляя
произвольно меняющую
прикладываемых
импульсов
,
и
суммируя одинаковые результаты от каждого импульса докажем
теорему
о
взаимности
перемещений для произвольно меняющейся силы
правлению
k
как
функция времени вызванное силой меняющейся по произвольному
закону во времени и приложенной по направлению
лению
j
, вызванному такой же силой но приложенной по направлению
Рассуждая
аналогично
тому как это сделано в
справедлива
также
и
для
изменяемой системы Здесь следует подчеркнуть что все рассужд
ния
относятся
лишь
к
малым
перемещениям что необходимо для со
свойств
системы
.
Теорема о взаимности реакций
нию
смещений
j
Z
и
k
Z
.
Рассмотрим сначала воздействие в виде внезапного смещения связи
1=
j
Z
в
момент
времени
0
=t
j
АРХИТЕКТУРЫ
И
СТРОИТ
ЕЛЬНЫХ
НАУК
_______________________________________________
_____________________________
.
l
jlj
M
GV
m
G
=
Нанесение мгновенного импульса по
двум направлениям: а
–
замер смещения по направлению
; б –
импульс в направлении
замер смещения по направлению
обобщенная
масса
,
соответствующая
обобщенной координате с
Таким образом
,
движение
системы
после
нанесения
импульса определилось
будет
:
...sin
2
22
22
2
+
+
−
te
M
VGV
tnkj
ω
ω
Если поменять степени
свободы
для
нанесения
импульса
и
замера перемещения см
и решить задачу
аналогичным
образом
,
то
получим
выражение тождественное
Действительно компоненты
вектора
формы
собственных
колебаний
формулу совершенно одинаково
.
Таким
обра
зом
:
и при учете сил сопротивления
.
Формула
(5)
выражает
теорему
о
взаимности перемещений
Представляя произвольно
меняющую
ся
во
времени
силу
,
как
действие последовательно
прикладываемых импульсов и
суммируя
одинаковые
результаты
от
каждого импульса докажем
теорему о взаимности перемещений
для
произвольно
меняющейся
силы
:
перемещение по н
функция времени, вызванное силой, меняю щейся по произвольному
закону во времени и приложенной по направлению
j
, равно перемещению по напра
вызванному такой же силой, но приложенной по направлению
Рассуждая аналогично
тому
,
как
это
сделано
в
[1]
,
можно
показать что теорема будет
справедлива также и для изменяемой
системы
.
Здесь
следует
подчеркнуть что все рассужд
ния относятся лишь к малым
перемещениям
,
что
необходимо
для
со
Теорема о взаимности реакций.
Пусть
на
систему
наложены
две связи по направл
Рассмотрим
сначала
воздействие
в
виде
внезапного смещения связи
0
.
Необходимо
определить
динамическую
реакцию в связи
k
j
_____________________________
87
–
импульс
импульс в направлении
,
обобщенная масса соответствующая обобщенной
координате
с
Таким образом движение системы после нанесения импульса
определилось
.
(4)
Если поменять степени свободы для нанесения импульса и замера
перемещения
(
см
.
и решить задачу аналогичным образом то получим выражение
тождественное
Действительно компоненты вектора формы собственных колебаний
j
V
и
k
V
вхдят
в
(5)
и при учете сил сопротивления Формула выражает теорему о взаимности
перемещений
ся во времени силу как действие
последовательно
прикладываемых импульсов и суммируя одинаковые результаты от каждого
импульса
,
докажем
перемещение по н
а-
функция времени вызванное силой меняющейся по произвольному
равно перемещению по напра
в-
вызванному такой же силой но приложенной по направлению
k
.
можно показать
,
что
теорема
будет
справедлива также и для изменяемой системы Здесь следует подчеркнуть
,
что
все
рассужд
е
-
ния относятся лишь к малым перемещениям что необходимо для со
хранения
линейных
Пусть на систему наложены две
связи
по
направл
е
-
Рассмотрим сначала воздействие в виде внезапного
смещения
связи
Необходимо определить динамическую
реакцию
в
связи
kj
r
k
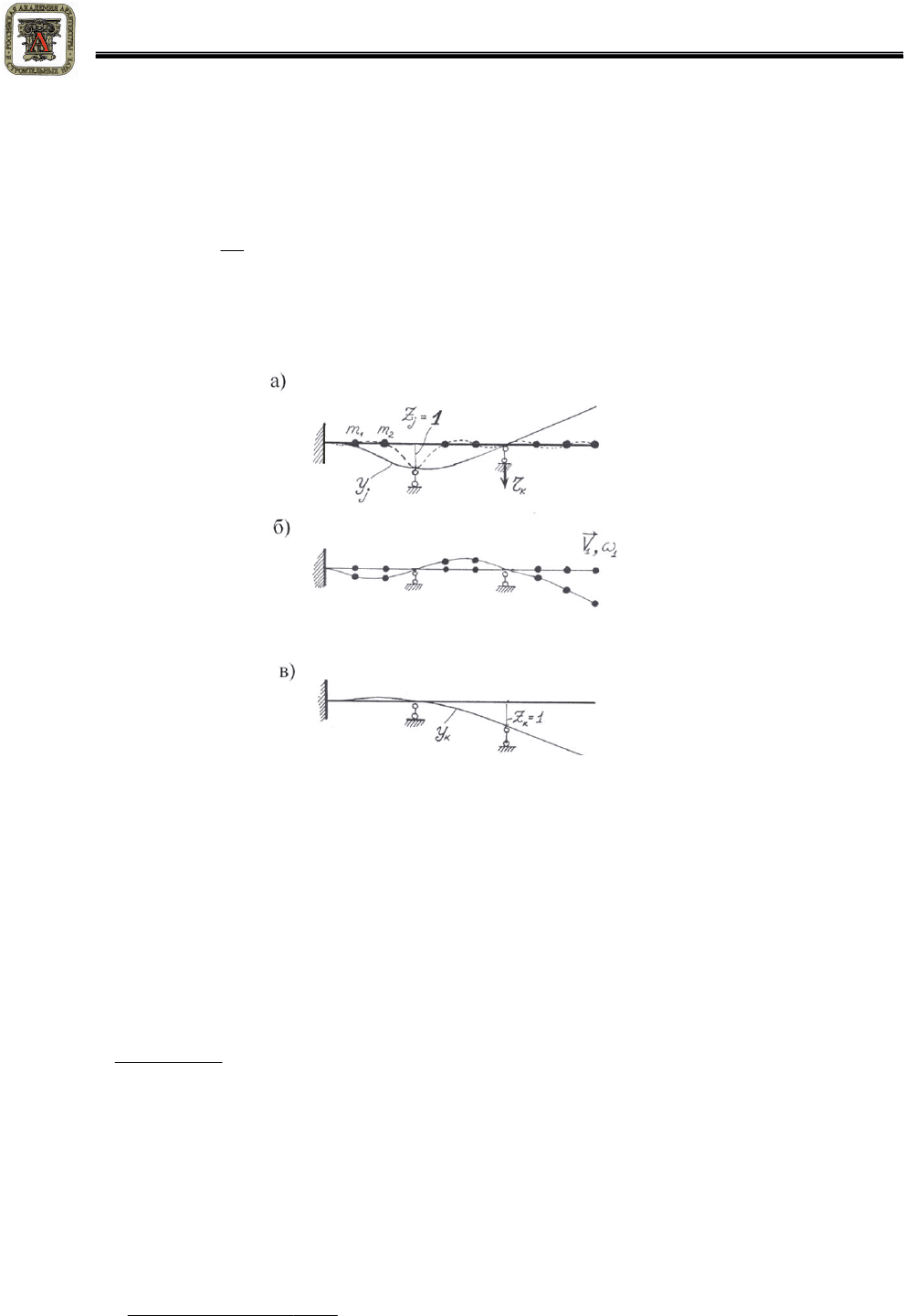
88
____________________________________________
(
см
.
рисунок
2,
а
).
Движение
системы
в
данном случае можно представить как свободные колебания в
круг
статического
прогиба
,
вызванного смещением
j
q
AVqAVytZ
rr
r
++=)(
22111
Здесь
sin(cos
t
n
teq
l
l
l
l
tn
l
l
ω
ω
ω
+=
−
Выбранные
частные
решения уравнения при нулевой правой части отвечают сл
дующим
начальным
условиям
:
Рисунок 2 –
К доказательству теоремы о взаимности
от смещения
1=
j
Z
и стартовое положение системы при внезапном смещении связи
(пунктир); б –
форма собственных колебаний системы с двумя наложенными связями
в –
статический прогиб от смещения связи
Постоянные
...,,
21
АА
следует определить из того условия чтобы в начальный м
мент
времени
точки
системы
,
несущие сосредоточенные массы имели нулевые начальные
смещения
.
Тогда
,
пользуясь
известной методикой определения движения по начальным у
ловиям
[5],
для
1
А
запишем
формулу пока рассмотр
1
1
1
M
mVy
A
iiij
∑
−
=
.
Теперь
можно
представить что в каждый момент времени на систему действуют силы
инерции
ii
Zm
&&
−
и
силы
сопротивления
ложим
их
как
статические
и
воспользуемся теоремой А А Гвоздева в ее статическом вариа
те
.
Придется
использовать
статический прогиб от единичного смещения
2,
в
)
2(
1
111
∑
−−−=
n
qVmAyr
iiikkj
&&
Подставляя
сюда
значение
1
1
)(
M
ymVy
r
ikiiij
kj
⋅
−=
∑ ∑
Формула
(9)
дает
не
полное значение реакции
РОССИЙСКАЯ
АКАДЕМИЯ
АРХИТЕКТУРЫ И СТРОИТ
МОСКВА
____________________________________________
_____________________________________________________________________
Движение системы в данном
случае
можно
представить
как
свободные колебания в
круг статического прогиба вызванного
смещением
1=
j
Z
.
nnn
qAV
q
r
++...
2
.
)
t
.
Выбранные частные решения
уравнения
(1)
при
нулевой
правой
части отвечают сл
дующим начальным условиям
:
0)0(1)0( ==
ll
qиq
&
.
К доказательству теоремы о взаимности
реакций: а –
статический прогиб системы
и стартовое положение системы при внезапном смещении связи
форма собственных колебаний системы с двумя наложенными связями
статический прогиб от смещения связи
1=
k
Z
следует
определить
из
того
условия
,
чтобы в начальный м
мент времени точки системы
,
несущие
сосредоточенные
массы
,
имели
нулевые начальные
пользуясь
известной
методикой
определения
движения по начальным у
запишем формулу
(
пока
рассмотр
им
только
первый
член ряда
Теперь можно представить
,
что
в
каждый
момент
времени
на
систему действуют силы
и силы сопротивления
ii
Znm
&
1
2−
.
Для
определения
реакции от этих сил пр
как статические и воспользуемся
теоремой
А
.
А
.
Гвоздева
в
ее
статическом вариа
те Придется использовать статический
прогиб
от
единичного
смещения
)
1
1
q
n
&
.
Подставляя сюда значение
из
(8),
получим
:
( )
111
1
2 qnq
Vm
ii
&&&
+
. (9)
Формула дает не полное
значение
реакции
kj
r
,
а
только
ее
переменную во времени
1
A
АРХИТЕКТУРЫ
И
СТРОИТ
ЕЛЬНЫХ
НАУК
МОСКВА
–
ОРЕЛ
–
КУРСК
, 2011
_____________________________________________________________________
Движение системы в данном случае можно представить как свободные
колебания
в
о
-
(6)
(7)
Выбранные частные решения уравнения при нулевой правой
части
отвечают
сл
е
-
статический прогиб системы
и стартовое положение системы при внезапном смещении связи
1=
j
Z
форма собственных колебаний системы с двумя наложенными связями;
следует определить из того условия чтобы
в
начальный
м
о
-
мент времени точки системы несущие сосредоточенные массы имели
нулевые
начальные
пользуясь известной методикой определения движения
по
начальным
у
с
-
им только первый
член
ряда
(6)):
(8)
Теперь можно представить что в каждый момент времени на систему
действуют
силы
Для определения реакции
от
этих
сил
пр
и
-
как статические и воспользуемся теоремой А А Гвоздева в ее
статическом
вариа
н
-
те Придется использовать статический прогиб от единичного смещения
1=
k
Z (
см
.
рисунок
. (9)
а только ее переменную
во
времени
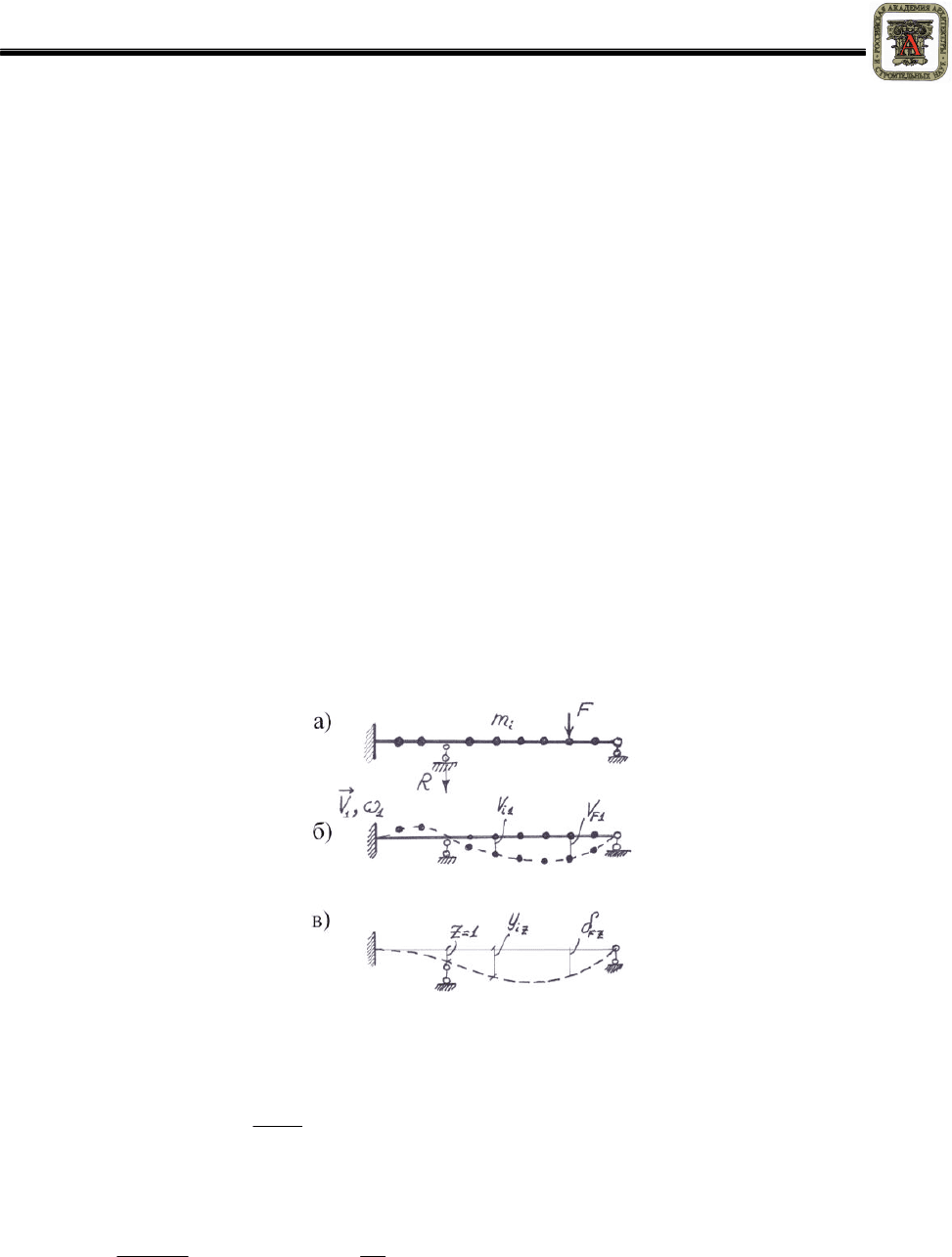
РОССИЙСКАЯ
АКАДЕМИЯ
АРХИТЕКТУРЫ И СТРОИТ
МОСКВА
–
ОРЕЛ
–
КУРСК
, 2011
_____________________________________
_______________________________________________
составляющую
.
Постоянная
составляющая соответствую
венно
подчиняется
теореме
взаимности поэтому далее рассмотрим лишь динамическую с
ставляющую
kj
r
.
Анализируя
формулу
(9)
видим что замена индексов
ции
.
Конечно
,
так
будет
н
е
только для первого члена ряда но для всех остальных слагаемых
учитывающих
высшие
формы
собственных колебаний Таким образом теорема о взаимности
реакций
доказана
для
внезапного смещения опоры и при учете сил сопротивления
Смещение
опоры
по
какому
как
комбинацию
элементарных внезапных смещений Тогда с привлечением принципа с
перпозиции
,
который
справедлив для линейной системы будет доказана терема о взаимн
сти
реакций
при
п
роизвольном
смещении во
)()( trtr
jkkj
=
.
Изменение
во
времени
реакции в связи
ному
закону
во
времени
,
всегда
будет равно изменению во времени реакции в связи
логичного
смещения
связи
k
.
Теорема о взаимности реакции и перемещен ия теорема А А Гвоздев
На
рисунке
3,
а
показана система к которой внезапно прикладывается сила
делим
реакцию
R
в
наложенной связи Решение будем вести раскладывая движение по со
ственным
формам
колебаний
.
Первая из этих форм показана на рис
Дифференциальное
уравнение для первой обобщенной координаты имеет вид
1
1
1
2
01111
2
M
FV
qqnq
F
=++
ω
&&&
.
Частное
решение
(1),
соответствующее
будет
:
−=
−
e
M
FV
q
tn
F
1
01
2
1
1
cos1
1
ω
ω
Для
любого
момента
времени можно представить что система загружена в каждой
−i
ой
точке
силами
инерции
и
силами сопротивления
тему
действует
сила
F
.
Для
определения реакции в наложенной связи воспользуемся теор
мой
Гвоздева
(
статический
вариант При этом потребуется статический
ном
смещении
связи
(
рисунок
3,
Выполнив
необходимые дифференцирования получим следующую формулу для и
АРХИТЕКТУРЫ
И
СТРОИТ
ЕЛЬНЫХ
НАУК
_______________________________________________
_____________________________
составляющую Постоянная составляющая
,
соответствую
щая
статическому прогибу естес
венно подчиняется теореме взаимности
,
поэтому
далее
рассмотрим
лишь динамическую с
Анализируя формулу
(9)
видим
,
что
замена
индексов
k
на
j
не
изменит значения реа
е только
для
первого
члена
ряда
,
но
для
всех
остальных слагаемых
учитывающих высшие формы
собственных
колебаний
.
Таким
образом
,
теорема о взаимности
реакций доказана для внезапного
смещения
опоры
и
при
учете
сил
сопротивления
Смещение опоры по какому
-
то
другому
закону
во
времени
всегда можно представить
как комбинацию элементарных
внезапных
смещений
.
Тогда
с
привлечением принципа с
перпозиции который справедлив
для
линейной
системы
,
будет
доказана терема о взаимн
роизвольном
смещении
во
времени
:
Изменение во времени
реакции
в
связи
k
,
вызванное
смещением
связи
ному закону во времени всегда
будет
равно
изменению
во
времени
реакции в связи
Теорема о взаимности реакции и перемещения (теорема А.А. Гвоздев
показана
система
,
к
которой
внезапно
прикладывается сила
в наложенной
связи
.
Решение
будем
вести
,
раскладывая движение по со
ственным формам колебаний
.
Первая
из
этих
форм
показана
на
рис
унке
3,
Рисунок 3
Дифференциальное уравнение
для
первой
обобщенной
координаты имеет вид
.
Частное решение соответствующее
нулевым
начальным
скоростям и смещениям
+ t
n
t
1
1
1
1
sin
ω
ω
ω
.
Для любого момента
времени
можно
представить
,
что
система
загружена в каждой
силами инерции
и
силами
сопротивления
)2(
1111
qnqVm
ii
&&&
−−
.
Кроме того на си
Для
определения
реакции
в
наложенной
связи
воспользуемся теор
мой Гвоздева статический вариант
).
При
этом
потребуется
статический
рисунок
3,
в
).
Выполнив необходимые
дифференцирования
,
получим
следующую формулу для и
_____________________________
89
щая статическому
прогибу
,
естес
т
-
венно подчиняется теореме взаимности поэтому далее рассмотрим лишь
динамическую
с
о
-
не изменит
значения
реа
к
-
е только для первого члена ряда но для всех
остальных
слагаемых
,
учитывающих высшие формы собственных колебаний Таким образом
,
теорема
о
взаимности
реакций доказана для внезапного смещения опоры и при учете сил сопротивления
.
другому закону во времени всегда
можно
представить
как комбинацию элементарных внезапных смещений Тогда с привлечением
принципа
с
у
-
перпозиции который справедлив для линейной системы будет доказана
терема
о
взаимн
о
-
(10)
вызванное смещением
связи
j
по
произволь
-
ному закону во времени всегда будет равно изменению во времени реакции
в
связи
j
от
ана
-
Теорема о взаимности реакции и перемещения теорема А А. Гвоздев
а).
показана система к которой внезапно прикладывается
сила
F
.
Опре
-
в наложенной связи Решение будем вести раскладывая
движение
по
со
б
-
3,
б
.
Дифференциальное уравнение для первой обобщенной координаты
имеет
вид
:
(11)
нулевым начальным скоростям
и
смещениям
,
(12)
Для любого момента времени можно представить что система
загружена
в
каждой
.
Кроме
того
,
на
си
с
-
Для определения реакции в наложенной связи
воспользуемся
теор
е
-
мой Гвоздева статический вариант При этом потребуется статический
прогиб
при
единич
-
Выполнив необходимые дифференцирования получим следующую
формулу
для
и
с
-
