Вестник отделения строительных наук РААСН 2011 №15
Подождите немного. Документ загружается.


РОССИЙСКАЯ АКАДЕМИЯ АРХИТЕК ТУРЫ И СТРОИТЕЛЬНЫХ НАУК
МОСКВА – ОРЕЛ – КУРСК, 2011
60
_________________________________________________________________________________________________________________
УДК
539.3
ГОРДОН
В
.
А
.,
КРАВЦОВА
Э
.
А
.
(
ФГОУ
ВПО
«
Госуниверситет
–
УНПК
»,
г
.
Орел
)
ВЛИЯНИЕ ПРОГРЕССИРУЮЩЕГО Р АССЛОЕНИЯ
НА НАПРЯЖЕННОЕ СОСТОЯНИЕ СОСТАВНОГО СТЕРЖНЯ
В
процессе
эксплуатации
в
несущей
конструкции
могут
происходить
необратимые
процессы
,
негативно
влияющие
на
ее
прочность
(
устойчивость
и
пр
.):
увеличиваются
дефор
-
мации
,
деградируют
опорные
связи
,
образуются
трещины
,
перераспределяются
напряжения
.
С
позиций
строительной
механики
при
этом
возникают
задачи
расчета
таких
систем
как
кон
-
структивно
нелинейных
.
Несмотря
на
то
,
что
это
направление
интенсивно
разрабатывается
[1-4],
методы
моделирования
и
расчетов
несущих
конструкций
,
учитывающие
квазистатиче
-
ские
и
внезапные
повреждения
,
частичные
разрушения
,
трещинообразование
и
другие
запро
-
ектные
воздействия
,
недостаточно
развиты
.
Поэтому
одной
из
актуальных
задач
современ
-
ной
строительной
механики
является
разработка
методов
аналитических
,
численных
и
экс
-
периментальных
,
которые
,
учитывая
изменение
расчетной
схемы
нагруженной
конструкции
,
описывали
бы
специфику
и
характеристики
статических
состояний
и
динамических
процессов
,
инициируемых
этими
изменениями
,
связывали
бы
уровни
приращений
напряжений
и
дефор
-
маций
с
параметрами
конкретных
повреждений
и
других
запроектных
воздействий
.
В
ряде
работ
[5-8]
представлены
математические
модели
динамических
процессов
,
возникающих
в
нагруженных
стержнях
,
балках
,
прямоугольных
и
круглых
пластинках
при
внезапных
изменениях
их
структуры
,
и
метод
их
исследования
.
В
этих
работах
в
расчетные
схемы
вводятся
повреждения
конструкции
типа
частичного
или
полного
обрыва
опорных
связей
,
выключения
из
работы
элементов
,
частичного
разрушения
(
изменения
размеров
),
об
-
разования
расслоений
и
трещин
.
Математическими
моделями
изучаемых
объектов
являются
дифференциальные
уравнения
различных
порядков
с
постоянными
и
переменными
коэффи
-
циентами
,
граничные
и
начальные
условия
,
ограничения
и
допущения
.
Комплексный
метод
формирования
аналитических
оценок
напряженно
-
деформированного
состояния
объектов
,
моделирующих
элементы
строительных
конструкций
,
включает
:
–
выполнение
статических
расчетов
для
заданных
нагрузок
с
целью
определения
де
-
формаций
и
внутренних
усилий
и
формирования
начальных
условий
для
возможного
пере
-
ходного
динамического
процесса
,
а
также
для
сравнительного
анализа
статического
и
дина
-
мического
состояний
–
расчет
частот
(
периодов
)
и
форм
(
мод
)
собственных
колебаний
видо
-
измененной
(
поврежденной
)
конструкции
;
–
расчет
вынужденных
движений
путем
разложения
исходного
состояния
по
модам
нового
состояния
.
Рассмотренные
в
этих
работах
задачи
объединяет
единый
метод
решения
дифферен
-
циальных
уравнений
,
описывающих
переходные
процессы
,
развивающиеся
при
импульсных
изменениях
нагрузок
,
условий
опирания
,
размеров
и
т
.
п
.
Решения
строятся
методом
Фурье
,
разложением
перемещений
и
нагрузок
по
формам
собственных
колебаний
видоизмененной
конструкции
и
применением
интеграла
Дюамеля
.
В
настоящей
работе
изучается
перераспределение
напряжений
в
нагруженной
балке
,
моделируемой
составным
(
по
А
.
Р
.
Ржаницыну
)
стержнем
.
Эта
балка
представляет
собой
часть
несущей
системы
крестообразной
формы
,
являющейся
элементом
каркаса
многоэтаж
-
ного
здания
[7, 9] (
рисунок
1).

РОССИЙСКАЯ АКАДЕМИЯ АРХИТЕК ТУРЫ И СТРОИТЕЛЬНЫХ НАУК
МОСКВА – ОРЕЛ – КУРСК, 2011
_________________________________________________________________________________________________________________
61
Рисунок 1 – Расчетные схемы: а – модель элемента каркаса многоэтажного здания;
б – цельная часть OD конструкции; в – верхняя часть элемента OD
Предполагается
,
что
связи
сдвига
между
двумя
одинаковыми
(
верхней
и
нижней
)
час
-
тями
нагруженной
балки
постепенно
обрываются
на
некотором
промежутке
x
1
x
2
,
что
изменяет
картину
напряженно
-
деформированного
состояния
.
Представляет
практический
интерес
связать
характер
и
степень
этих
возможных
изменений
с
локализацией
и
величиной
расслоения
и
скоростью
его
распространения
.
Далее
предполагается
,
что
связи
,
соединяющие
обе
части
стержня
,
равномерно
рас
-
пределены
вдоль
оси
,
а
касательные
напряжения
(1),
возникающие
в
слоях
,
параллельных
нейтральному
,
распределены
равномерно
по
ширине
прямоугольного
продольного
(
и
по
-
перечного
)
сечения
балки
:
(
)
−==
2
1
4
2
2
y
h
z
I
xQ
yxxy
ττ
, (1)
где
( )
−= xlqxQ
8
5
–
перерезывающая
сила
в
сечении
x;
12
3
bh
z
I =
–
осевой
момент
инерции
поперечного
сечения
;
−∈
2
,
2
1
hh
y
–
расстояние
произвольного
слоя
от
нейтрального
.
Наибольшие
значения
касательные
напряжения
принимают
в
нейтральном
слое
по
которому
происходит
расслоение
(
рисунок
1,
в
):
−= xl
bh
q
yx
8
5
2
3
max
τ
. (2)
В
цельной
балке
касательные
напряжения
,
действующие
в
продольных
слоях
,
взаим
-
но
уравновешиваются
.
Обрыв
связей
сдвига
приводит
к
высвобождению
упругой
энергии
,
вызывающей
перераспределение
усилий
,
приложенных
к
выделенной
части
.
Алгоритм
рас
-
чета
расслоившейся
балки
состоит
из
следующих
операций
:
–
при
моделировании
расслоения
по
определенному
слою
вначале
рассматривается
изолированная
часть
(
например
,
верхняя
),
к
которой
приложены
внешние
нагрузки
и
усилия
,
действующие
со
стороны
отброшенной
части
(
рисунок
1,
в
);
–
к
местам
разрывов
связей
прикладываются
с
обратным
знаком
силы
,
действующие
через
связи
со
стороны
удаленной
части
,
равные
равнодействующей
распределенных
каса
-
тельных
напряжений
на
участках
расслоения
,
что
равносильно
обнулению
касательных
на
-
пряжений
на
этих
участках
.
При
этом
выполняются
проверочные
расчеты
,
чтобы
убедиться
в
эквивалентности
замены
связей
сдвига
соответствующими
распределенными
усилиями
;
–
рассчитываются
напряжения
и
деформации
в
выделенной
части
от
действия
всей
совокупности
усилий
,
приложенных
к
этой
части
.
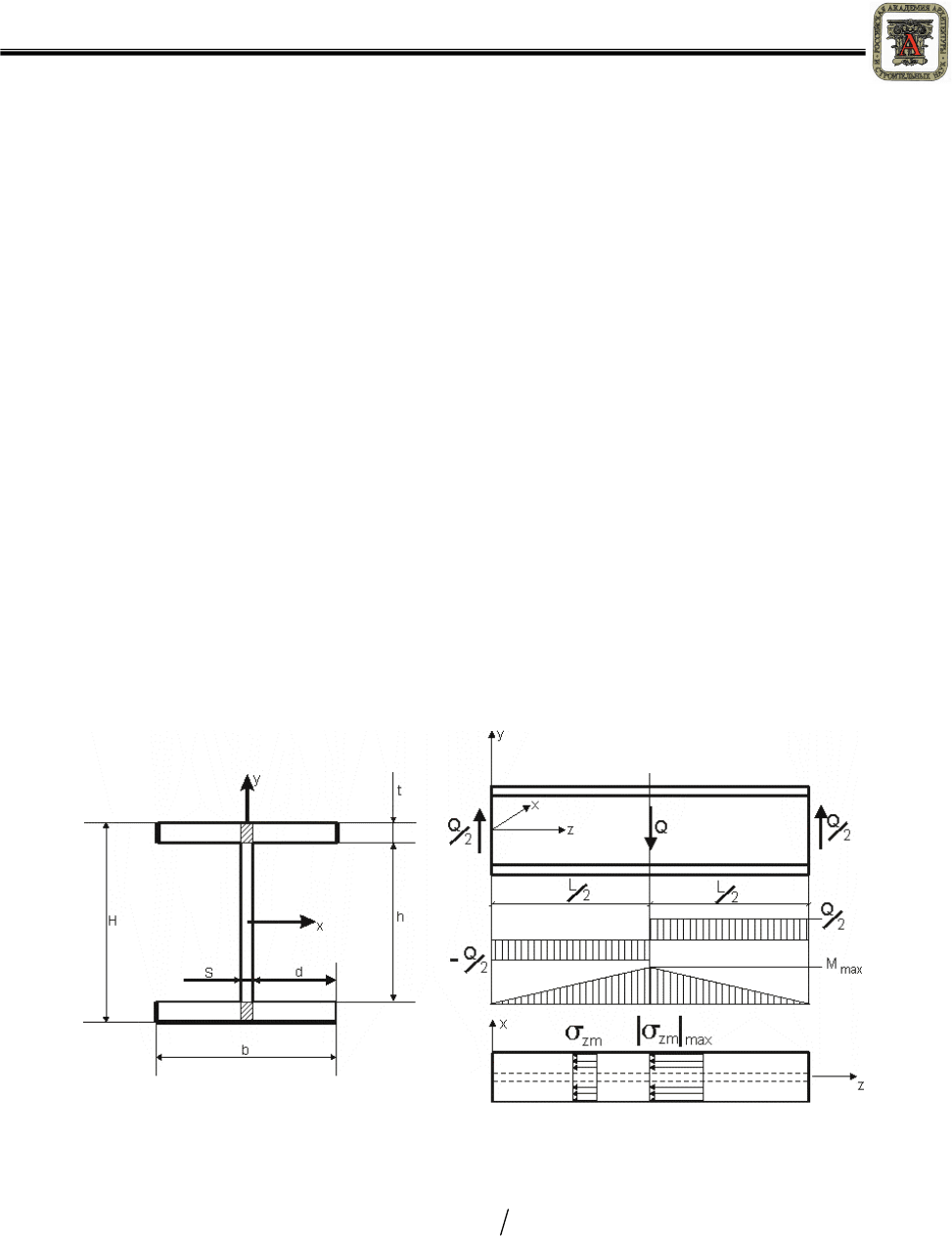
На
рисунке
2
изображены
нагрузки
,
действующие
на
верхнюю
часть
составной
балки
при
частичном
расслоении
.
(
)
(
)
lxxxx ,0,,
2
1
2
1
∈<
b
yx
τ
,0
1
=y

РОССИЙСКАЯ АКАДЕМИЯ АРХИТЕК ТУРЫ И СТРОИТЕЛЬНЫХ НАУК
МОСКВА – ОРЕЛ – КУРСК, 2011
62
_________________________________________________________________________________________________________________
Рисунок 2 – Нагрузки, действующие на верхнюю часть составной балки
при частичном расслоении (от
ξξξξ
1
до
ξξξξ
2
)
Нормальные
безразмерные
напряжения
в
крайнем
верхнем
волокне
на
трех
участ
-
ках
определяются
из
следующих
соотношений
[10]:
( ) ( )
( ) ( )
( ) ( )
≤≤
−−+−−−
≤≤
−−+−−−
≤≤
−−
−−
−++−−−
==
.1
2
,
2
8
5
64
9
31
4
3
2
16
;
21
,
2
2
8
5
64
9
31
4
3
2
16
;
1
0,
2
8
5
2
2
8
5
2
1
8
5
64
9
31
4
3
2
16
2
2
ξξξξξ
ξξξξξξ
ξξξξξξξ
σσ
ql
bh
(3)
Здесь
ξ
обозначена
безразмерная
осевая
координата
l
x
=
ξ
.
Анализ
наибольших
растягивающих
и
сжимающих
напряжений
в
стержне
в
зависимости
от
параметров
расслоения
(
размеров
и
локализации
)
для
двух
случаев
распространения
расслое
-
ния
(1:
от
правой
опоры
–
налево
; 2:
от
левой
заделки
–
направо
)
приведен
в
работе
[10].
В
общем
случае
,
для
учета
эффекта
динамики
в
расчетной
программе
необходимо
за
-
дать
зависимость
величины
обнуляемых
сил
от
времени
,
что
равносильно
заданию
зависи
-
мости
от
времени
длины
участка
расслоения
.
Вид
такой
зависимости
может
быть
различным
для
разных
конструктивных
схем
,
материалов
,
уровней
нагружения
и
т
.
д
.
и
устанавливается
экспериментально
[11].
На
стадии
предварительного
проектирования
можно
принять
линей
-
ную
или
квадратичную
зависимость
длины
образовавшегося
расслоения
(
)
lll
pp
≤≤0
от
вре
-
мени
.
При
этом
безразмерный
промежуток
времени
изменения
длины
расслоившегося
участ
-
ка
от
нуля
до
значения
можно
принимать
в
долях
от
времени
полного
расслоения
,
ко
-
торое
определяется
как
отношение
длины
стержня
l
к
средней
скорости
распространения
расслоения
ср
V
,
то
есть
П
t
t
=
τ
,
.
ср
П
V
l
t =
При
этом
,
например
,
для
первого
случая
[10]
====
2,1,,1var,
21
i
l
x
i
i
ξξξ
справед
-
ливы
следующие
соотношения
:
1
xll
p
−=
или
в
безразмерном
виде
:
l
l
ll
p
pp
=ξ−= ,1
1
.
Пусть
является
решением
дифференциального
уравнения
:
ср
p
V
dt
dl
=
, (4)
то
есть
предполагается
,
что
расслоение
распространяется
от
правого
конца
налево
с
посто
-
янной
скоростью
ср
V
(
точка
x
1
движется
налево
с
постоянной
скоростью
).
Тогда
из
уравнения
(4)
следует
tVl
ср
p
=
или
в
безразмерном
виде
:
σ
τ
П
t
p
l
РОССИЙСКАЯ АКАДЕМИЯ АРХИТЕК ТУРЫ И СТРОИТЕЛЬНЫХ НАУК
МОСКВА – ОРЕЛ – КУРСК, 2011
_________________________________________________________________________________________________________________
63
τξτ
−== 1,
1p
l
. (5)
Подставляя
(5)
и
1
2
=
ξ
в
соотношения
(3),
получим
,
в
частности
,
наибольшее
растягивающее
напряжение
в
точке
А
(
рисунок
2)
крайнего
верхнего
волокна
:
.
4
1
)1(3
2
3
),0(
+−−=
τττσ
Предполагая
,
что
расслоение
достигает
произвольной
длины
p
l
по
закону
:
n
p
l
τ
=
, (6)
где
n
–
произвольная
константа
,
получим
формулу
для
напряжения
в
точке
А
вида
:
( )
+−−=
nn
τττσ
4
1
13
2
3
),0(
. (7)
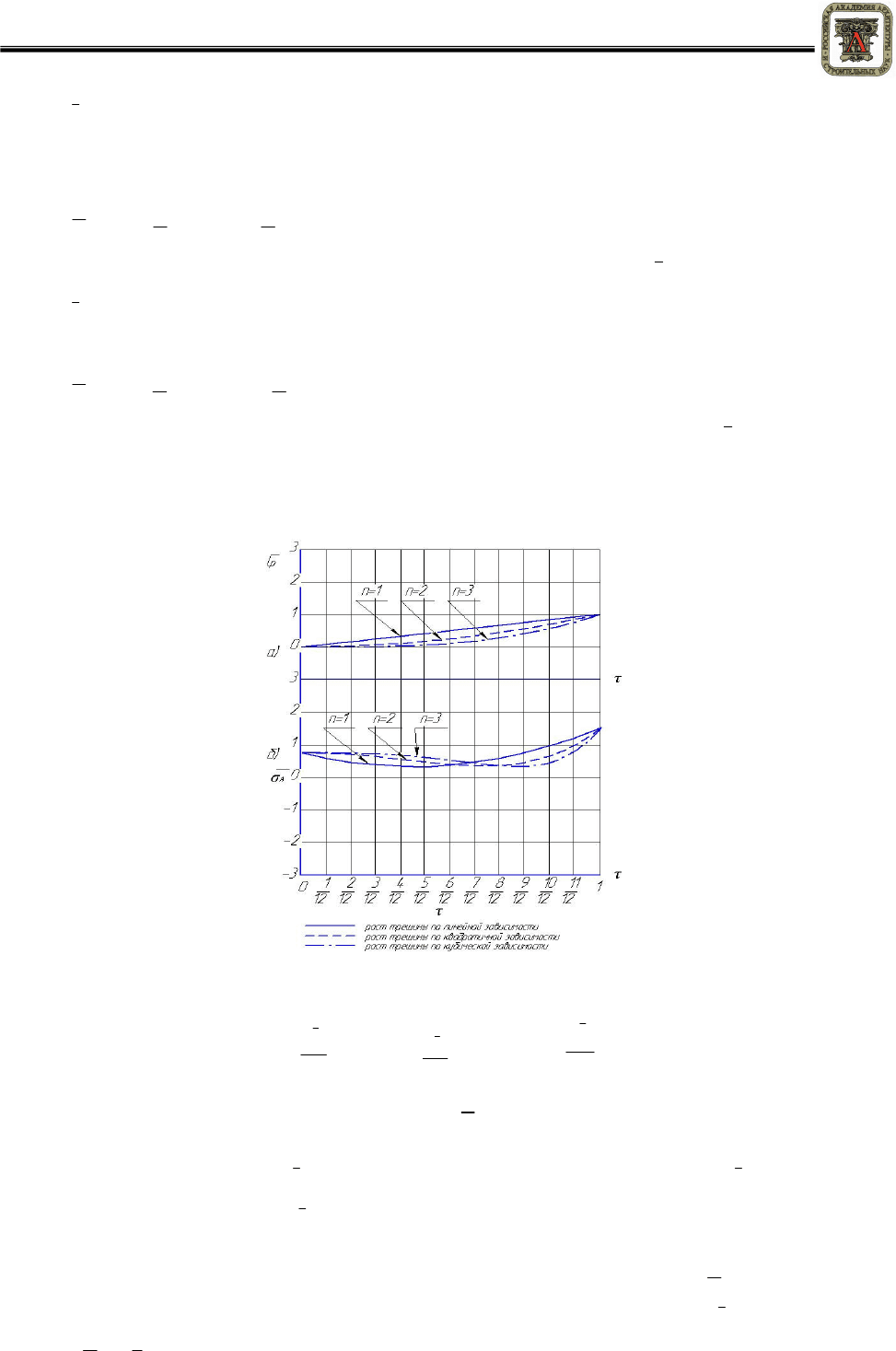
На
рисунке
3
изображены
графики
зависимости
длины
расслоения
p
l
(
а
)
и
наиболь
-
шего
растягивающего
напряжения
в
точке
А
(
б
)
от
времени
τ
,
рассчитанные
для
случая
рас
-
пространения
расслоения
справа
налево
по
формулам
(6)
и
(7).
Рисунок 3 – Временные зависимости:
а – длины расслоения; б – напряжения в точке А
(
1,1 ==
τ
d
ld
n
p
;
;2,2
τ
τ
==
d
ld
n
p
2
3,3
τ
τ
==
d
ld
n
p
)
Наибольшее
растягивающее
напряжение
А
σ
с
ростом
длины
участка
расслоения
изме
-
няется
немонотонно
(
рисунок
3,
б
).
Вначале
с
ростом
этого
участка
напряжение
убывает
от
значения
0,75 (
цельная
балка
0=
p
l
)
до
минимального
значения
0,328
при
375
,0=
p
l
,
затем
возрастает
до
значения
1,5
при
1=
p
l
(
полное
расслоение
).
При
этом
длительность
стадии
поч
-
ти
двукратного
снижения
напряжения
тем
больше
,
чем
больше
показатель
n
функции
(6)
и
,
на
-
оборот
,
возрастание
напряжения
от
минимума
до
наибольшего
значения
5,1=
А
σ
тем
круче
,
чем
больше
n
.
Следует
также
отметить
,
что
при
нелинейной
зависимости
(
)
(
)
1>= nfl
p
τ
на
кривых
(
)
ττσ
AА
=
появляются
точки
перегиба
,
то
есть
для
больших
значений
n
характерна
малая
скорость
изменения
напряжений
на
стадии
снижения
с
0,75
до
0,328
и
резкое
ускорение

РОССИЙСКАЯ АКАДЕМИЯ АРХИТЕК ТУРЫ И СТРОИТЕЛЬНЫХ НАУК
МОСКВА – ОРЕЛ – КУРСК, 2011
64
_________________________________________________________________________________________________________________
процесса
нарастания
напряжения
после
достижения
значения
375
,0=
p
l
.
Предельный
случай
,
когда
произвольное
расслоение
(
)
∞→→
срp
Vtl ,0
образуется
мгновенно
,
требует
учета
инер
-
ционных
сил
.
Такой
подход
к
анализу
динамических
догружений
в
стержневых
системах
при
-
меняется
при
внезапном
(
t
= 0)
и
полном
(
)
1,0
21
==
ξξ
расслоении
консоли
[5]
и
двухопор
-
ной
балки
[7, 12]
на
две
части
.
Настоящая
работа
является
обобщением
работы
[7, 12]
на
случай
частичного
(
)
1var,
21
==
ξξ
квазистатического
расслоения
.
Результаты
работы
необходимы
для
сравне
-
ния
получаемых
приращений
напряжений
с
динамическими
приращениями
,
развивающимися
при
внезапном
расслоении
.
Библиографический список
1.
Бондаренко
,
В
.
М
.
Износ
,
повреждения
и
безопасность
железобетонных
сооружений
[
Текст
] /
В
.
М
.
Бондаренко
,
А
.
В
.
Боровских
. –
М
.:
ИД
Русанова
, 2000. – 144
с
.
2.
Гениев
,
Г
.
А
.
Прочность
и
деформативность
железобетонных
конструкций
при
за
-
проектных
воздействиях
[
Текст
] /
Г
.
А
.
Гениев
,
В
.
И
.
Колчунов
,
Н
.
В
.
Клюева
,
А
.
И
.
Никулин
,
К
.
П
.
Пятикрестовский
. –
М
.:
АСВ
, 2004. – 216
с
.
3.
Клюева
,
Н
.
В
.
Основы
теории
живучести
железобетонных
конструктивных
систем
при
запроектных
воздействиях
:
дис
. …
докт
.
техн
.
наук
: 05.23.01 [
Текст
] /
Н
.
В
.
Клюева
. –
Орел
, 2009. – 441
с
.
4.
Трифонов
,
О
.
В
.
Анализ
безопасности
и
форм
разрушения
конструкций
при
много
-
компонентных
динамических
воздействиях
[
Текст
] /
О
.
В
.
Трифонов
,
В
.
П
.
Чирков
//
Строи
-
тельная
механика
и
расчет
сооружений
. – 2008, –
№
6. –
С
. 38-46.
5.
Павлова
,
Т
.
А
.
Развитие
метода
расчета
строительных
конструкций
на
живучесть
при
внезапных
структурных
изменениях
:
дис
. …
канд
.
техн
.
наук
: 05.23.17 [
Текст
] /
Т
.
А
.
Пав
-
лова
. –
Орел
, 2006. – 175
с
.
6.
Брусова
,
В
.
И
.
Переходные
процессы
в
круглых
пластинах
и
балках
при
некоторых
внезапных
запроектных
воздействиях
:
дис
. …
канд
.
техн
.
наук
: 05.23.17 [
Текст
] /
В
.
И
.
Брусова
. –
Орел
, 2009. – 150
с
.
7.
Потураева
,
Т
.
В
.
Переходные
процессы
в
балках
при
внезапных
структурных
пере
-
стройках
и
трещинообразовании
:
дис
. …
канд
.
техн
.
наук
: 05.23.17 [
Текст
] /
Т
.
В
.
Потураева
. –
Орел
, 2009. –143
с
.
8.
Холодов
,
А
.
А
.
Динамические
явления
в
стержневых
системах
при
изменениях
их
структуры
:
дисс
. …
канд
.
техн
.
наук
: 01.02.04 [
Текст
] /
А
.
А
.
Холодов
. –
Тула
, 2009. – 116
с
.
9.
Гордон
,
В
.
А
.
Расчет
динамических
усилий
в
конструктивно
-
нелинейных
элементах
стержневых
систем
при
внезапных
структурных
изменениях
[
Текст
] /
В
.
А
.
Гордон
,
Н
.
В
.
Клюе
-
ва
,
А
.
С
.
Бухтиярова
,
Т
.
В
.
Потураева
//
Строительная
механика
и
расчет
сооружений
. – 2008. –
№
6. –
С
. 26-30.
10.
Гордон
,
В
.
А
.
Перераспределение
напряжений
в
нагруженной
составной
балке
при
деградации
связей
сдвига
[
Текст
] /
В
.
А
.
Гордон
,
Э
.
А
.
Кравцова
//
Строительная
механика
и
расчет
сооружений
. – 2010. –
№
4. –
С
. 2-6.
11.
Канчели
,
Н
.
В
.
К
оценке
безопасности
большепролетных
мембранных
покрытий
[
Текст
] /
М
.
В
.
Канчели
,
Ю
.
И
.
Кудишин
,
П
.
А
.
Батов
,
Д
.
Ю
.
Дробот
//
Строительные
материалы
,
оборудование
,
технологии
XXI
века
. – 2008. –
№
5(112). –
С
. 80-83.
12.
Гордон
,
В
.
А
.
Динамические
догружения
стержневой
конструкции
в
результате
внезапного
расслоения
ее
элементов
[
Текст
] /
В
.
А
.
Гордон
,
Т
.
В
.
Потураева
//
Материалы
ме
-
ждународной
научной
конференции
«
Современные
проблемы
математики
,
механики
,
ин
-
форматики
». –
Тула
:
ТулГУ
, 2009. –
С
. 259-260.
РОССИЙСКАЯ АКАДЕМИЯ АРХИТЕК ТУРЫ И СТРОИТЕЛЬНЫХ НАУК
МОСКВА – ОРЕЛ – КУРСК, 2011
_________________________________________________________________________________________________________________
65
УДК
624.071.3
ГРУДЕВ И.Д.
(ЦНИИПСК им. Мельникова, г. Москва)
АНАЛИЗ НАПРЯЖЕНИЙ В БАЛКЕ ДВУТАВРОВОГО СЕЧЕНИЯ
В УСЛОВИЯХ ПОПЕРЕЧНОГО ИЗГИБА
Балки
двутаврового
сечения
считаются
хорошо
изученными
,
а
формулы
для
их
расче
-
та
и
конструирования
сварных
двутавров
многократно
подтвержденными
практикой
проек
-
тирования
и
строительства
[1-3].
Однако
любой
грамотный
инженер
,
прочтя
эту
и
следую
-
щую
статьи
,
поймет
,
что
формулы
для
проверки
несущей
способности
двутавровых
балок
,
работающих
на
изгиб
,
неверны
по
своей
постановке
,
а
формулы
для
подбора
параметров
се
-
чения
не
определяют
предельного
состояния
двутавра
.
В
предлагаемой
статье
рассматривается
только
первая
часть
задачи
,
а
именно
,
прово
-
дится
анализ
напряженного
состояния
балки
двутаврового
сечения
при
поперечном
изгибе
с
позиций
теории
упругости
,
а
в
следующей
статье
будет
дана
формулировка
предельного
со
-
стояния
такой
балки
и
метод
расчета
несущей
способности
по
этому
предельному
состоянию
.
Вначале
для
анализа
напряженного
состояния
балки
двутаврового
сечения
целесооб
-
разно
рассмотреть
классическую
задачу
об
изгибе
балки
шарнирно
опертой
по
концам
и
на
-
груженной
поперечной
сосредоточенной
силой
в
середине
пролета
.
Расчетная
схема
такой
балки
и
принятая
система
координат
показаны
на
рисунке
1.
Рисунок 1 – Расчетная схема поперечного изгиба двутавровой балки
Левая
и
правая
половины
балки
симметричны
с
точностью
до
знака
,
поэтому
ниже
рассматривается
только
левая
половина
(
)
0 z L 2
≤ ≤
.
Если
сделать
обычное
допущение
о
том
,
что
реакции
опор
также
как
и
внешняя
попе
-
речная
нагрузка
в
середине
пролета
приложены
только
к
стенке
(
такой
тип
опирания
и
нагру
-
жения
в
эксперименте
осуществить
не
составляет
труда
),
то
полки
оказываются
совершенно
не
нагруженными
внешними
усилиями
(
рисунок
1).
В
то
же
время
продольные
напряжения
в
них
при
обычных
гибкостях
являются
наибольшими
по
абсолютной
величине
в
поперечном
сечении
.
Естественно
встает
вопрос
,
каким
образом
возникают
эти
напряжения
.
Для
суждения
о
напряжениях
в
полках
и
в
стенке
двутавра
целесообразно
проанали
-
зировать
уравнения
равновесия
теории
упругости
[4]
применительно
к
двутавровому
сече
-
нию
.
Учитывая
свойство
парности
касательных
напряжений
:
z
σ
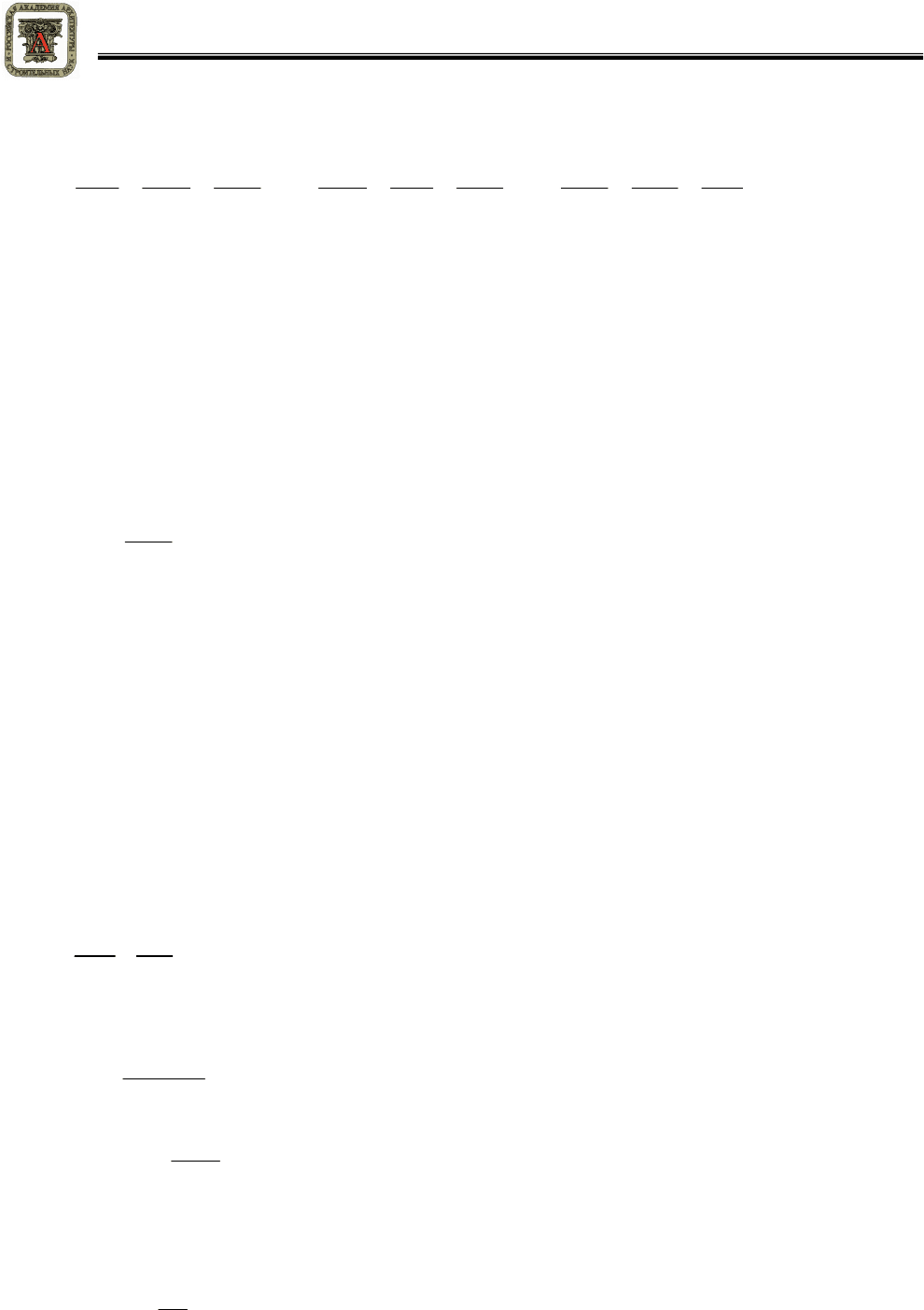
РОССИЙСКАЯ АКАДЕМИЯ АРХИТЕК ТУРЫ И СТРОИТЕЛЬНЫХ НАУК
МОСКВА – ОРЕЛ – КУРСК, 2011
66
_________________________________________________________________________________________________________________
,
имеем
. (1)
В
рассматриваемой
задаче
для
двутавра
в
целом
следует
учесть
очевидные
соотношения
:
. (2)
Напряжения в стенке
.
Касательные
напряжения
строго
равны
нулю
на
боковых
гранях
стенки
,
поэтому
в
первом
приближении
можно
считать
эти
напряжения
нулевыми
во
всех
точках
стенки
.
Таким
образом
,
первое
уравнение
равновесия
(1)
для
стенки
удовлетворяется
тождественно
.
Кроме
того
,
с
большой
точностью
можно
считать
,
что
касательные
напряжения
постоянны
по
толщине
стенки
,
то
есть
.
Второе
уравнение
(1)
сводится
к
со
-
отношению
,
откуда
следует
:
. (3)
Касательные
напряжения
в
стенке
существенны
,
так
как
именно
они
восприни
-
мают
перерезывающую
силу
:
, (4)
где
–
нагрузка
(
перерезывающая
сила
) (
рисунок
1); –
толщина
стенки
; –
высота
стенки
.
Правая
часть
соотношения
(4)
не
зависит
от
z,
поэтому
для
рассматриваемой
задачи
перерезывающая
сила
постоянна
как
в
левой
,
так
и
в
правой
половинах
балки
(
ри
-
сунок
1).
Третье
уравнение
равновесия
теории
упругости
для
стенки
двутавра
сводится
к
следующему
:
. (5)
В
соответствии
с
гипотезой
плоских
сечений
напряжения
не
зависят
от
поперечной
координаты
«
х
» (
рисунок
1),
а
вдоль
вертикальной
координаты
«y»
они
изменяются
линейно
:
, (6)
причем
напряжения
в
нижнем
и
верхнем
волокнах
определяются
моментом
:
, (7)
где
–
момент
сопротивления
двутавра
.
В
соответствии
с
балочным
уравнением
равновесия
момент
выражается
через
перере
-
зывающую
силу
так
(
рисунок
1):
. (8)
Из
последних
трех
уравнений
для
сжатого
верхнего
волокна
левой
половины
балки
следует
:
xy yx yz zy, xz zx
,
τ = τ τ = τ τ = τ
xy yx y yz zy
x xz zx z
0; 0; 0
x y z x y z x y z
∂τ ∂τ ∂σ ∂τ ∂τ
∂σ ∂τ ∂τ ∂σ
+ + = + + = + + =
∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂
x y xy
0, 0, 0
σ ≡ σ ≡ τ ≡
xz
τ
xz
0
τ ≡
zy
τ
zy zy
(y,z)
τ = τ
zy
0
z
∂τ
=
∂
zy zy
(y)
τ = τ
zy
τ
h / 2
zy
h /2
Q/ 2 Sdy
−
= τ
∫
Q 0
<
S
h
Q Const
=
zy
z
0
y z
∂τ
∂σ
+ =
∂ ∂
z
σ
zm
z
2 (z)
y
H
σ
σ =
zm
b
M(z)
(z)
W
σ = ±
b
W
Qz
M(z)
2
= −
РОССИЙСКАЯ АКАДЕМИЯ АРХИТЕК ТУРЫ И СТРОИТЕЛЬНЫХ НАУК
МОСКВА – ОРЕЛ – КУРСК, 2011
_________________________________________________________________________________________________________________
67
,
где
–
момент
инерции
двутавра
. (9)
Уравнение
(5)
с
учетом
соотношений
(3)
и
(9),
можно
теперь
переписать
так
:
. (10)
Полученное
уравнение
легко
интегрируется
,
в
результате
чего
получается
:
(11)
очевидно
,
что
константа
интегрирования
равна
максимальному
(
по
аб
-
солютной
величине
)
касательному
напряжению
в
сечении
балки
,
которое
может
быть
опре
-
делено
из
соотношения
(4):
, (12)
где
–
площадь
сечения
стенки
.
Откуда
следует
:
, (13)
где
–
замечательный
безразмерный
параметр
сечения
.
Окончательно
для
касательных
напряжений
в
стенке
получается
выражение
:
. (14)
Полученное
соотношение
соответствует
формуле
Журавского
,
применительно
к
стен
-
ке
двутаврового
сечения
.
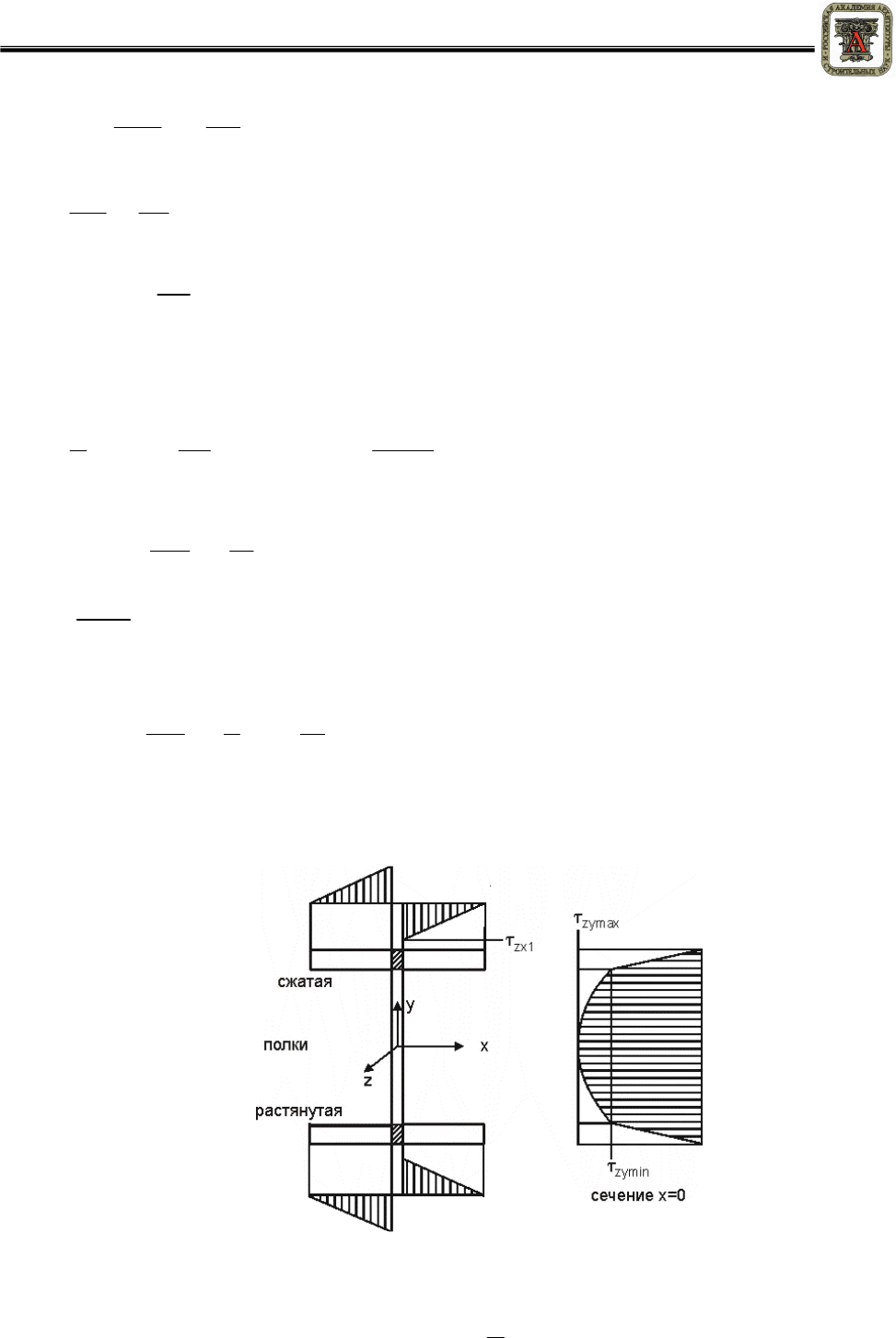
Эпюра
касательных
напряжений
показана
на
рисунке
2.
Рисунок 2 – Касательные напряжения в поперечном сечении двутавра
В
соответствии
с
формулой
(14)
при
,
то
есть
в
верхнем
и
нижнем
сечениях
стенки
,
касательные
напряжения
по
модулю
минимальны
и
равны
:
z
b b
Q Q
yz yz
W H 2J
σ = =
b
J
zy
b
d
Q
y
dy 2J
τ
= −
2
zy
b
Q
(y) y C
4J
τ = − +
zy zymax
C (0)
= τ = τ
h / 2
2
2
c
yzmax c zymax
b b
h / 2
QA hQ Q
S y dy A
2 4J 48J
−
= − + τ = − + τ
∫
c
A hS
=
zymax
c
Q B
1
2A 24
τ = +
2
c
b
A h
B
J
=
zy
τ
2
zy
c
Q B 2y
(y) 1 1 3
2A 6 h
τ = + −
zy
(y)
τ
h
y
2
= ±

РОССИЙСКАЯ АКАДЕМИЯ АРХИТЕК ТУРЫ И СТРОИТЕЛЬНЫХ НАУК
МОСКВА – ОРЕЛ – КУРСК, 2011
68
_________________________________________________________________________________________________________________
, (15)
а
при
касательное
напряжение
строго
равно
нулю
(
рисунок
2).
Отношение
максимального
и
минимального
касательных
напряжений
в
стенке
определяется
только
па
-
раметром
сечения
В
и
получается
следующим
. (16)
Для
нормальных
,
широкополочных
и
колонных
прокатных
двутавров
с
параллельны
-
ми
гранями
полок
в
рамках
сокращенного
сортамента
величина
параметра
В
колеблется
в
пределах
,
откуда
для
отношения
этих
напряжений
получается
оценка
:
.
Напряжения в полках
.
Учитывая
,
что
касательные
напряжения
строго
равны
нулю
на
горизонтальных
поверхностях
полок
,
в
первом
приближении
их
можно
считать
пре
-
небрежимо
малыми
во
всех
точках
сечений
полок
,
за
исключением
областей
пересе
-
чения
полок
со
стенкой
,
заштрихованных
на
рисунках
1
и
2.
Первое
уравнение
равновесия
теории
упругости
дает
: ,
то
есть
эти
напряже
-
ния
не
зависят
от
координаты
z.
Учитывая
,
кроме
того
,
что
касательные
напряже
-
ния
можно
считать
постоянными
по
толщине
полок
,
то
есть
независимыми
от
коорди
-
наты
«
у
».
Откуда
следует
,
что
.
Таким
образом
,
первые
два
уравнения
системы
(1)
выполняются
тождественно
.
В
первом
приближении
положение
полок
можно
охаракте
-
ризовать
значением
,
тогда
третье
уравнение
(1)
с
учетом
(9)
для
сжатой
полки
дает
:
. (17)
Это
уравнение
легко
интегрируется
и
в
результате
получается
:
. (18)
Константа
интегрирования
С
определяется
из
условия
на
краях
полки
при
для
правой
половины
сжатой
полки
плюс
и
для
левой
минус
,
откуда
следует
:
. (19)
Окончательно
распределение
касательных
напряжений
получается
следующим
:
. (20)
Аналогично
для
растянутой
полки
получается
:
.
Эпюры
этих
напряжений
показаны
на
рисунке
2.
По
-
видимому
,
впервые
(
автор
может
ошибаться
)
касательные
напряжения
при
-
ведены
в
книге
Работнова
Ю
.
Н
. [4].
zymin
c
Q B
1
2A 3
τ = −
H
y
2
= ±
zy
0
τ =
(
)
( )
zymin
zymax
1 B 3
1 B 6
τ
−
=
τ +
B 0.22 0.63
= ÷
zy
τ
yz
0
τ ≅
xz
0
z
∂τ
=
∂
t H,b
<<
xz
τ
xz xz
(x)
τ = τ
H
y
2
=
xz
b
d Q
dx 2W
τ
= −
xz
b
Q
x C
2W
τ = − +
xz
0
τ =
x b /2
= ±
b
Qb
C
4W
= ±
xz
b
Qb 2x
1
4W b
τ = ± −
xz
b
Qb 2x
1
4W b
τ = − ± −
xz
τ
zymin
zymax
0.80 0.09
τ
= ±
τ
РОССИЙСКАЯ АКАДЕМИЯ АРХИТЕК ТУРЫ И СТРОИТЕЛЬНЫХ НАУК
МОСКВА – ОРЕЛ – КУРСК, 2011
_________________________________________________________________________________________________________________
69
Наибольшее
по
модулю
касательное
напряжение
в
пределах
свеса
полки
,
обозначен
-
ное
,
соответствует
значению
и
равно
:
. (21)
Для
наглядности
целесообразно
сравнить
касательные
напряжения
в
стенке
и
в
полках
двутавра
.
Для
этого
рассчитано
следующее
отношение
в
рамках
сокращенного
сортамента
:
Следует
особо
подчеркнуть
,
что
это
отношение
определяется
только
размерами
эле
-
ментов
поперечного
сечения
.
В
рассматриваемой
задаче
перерезывающие
силы
,
а
,
следовательно
,
и
касательные
напряжения
в
полках
не
зависят
от
продольной
координаты
«z» (
в
каждой
половине
по
длине
),
поэтому
в
строгой
постановке
парные
к
этим
напряжениям
должны
были
бы
быть
приложены
и
в
опорных
сечениях
z=0
и
z=L.
Проведенный
анализ
показывает
,
что
нормальные
напряжения
являются
результа
-
том
накопления
действующих
напряжений
в
точности
так
же
,
как
в
задаче
с
висячим
стержнем
,
показанным
на
рисунке
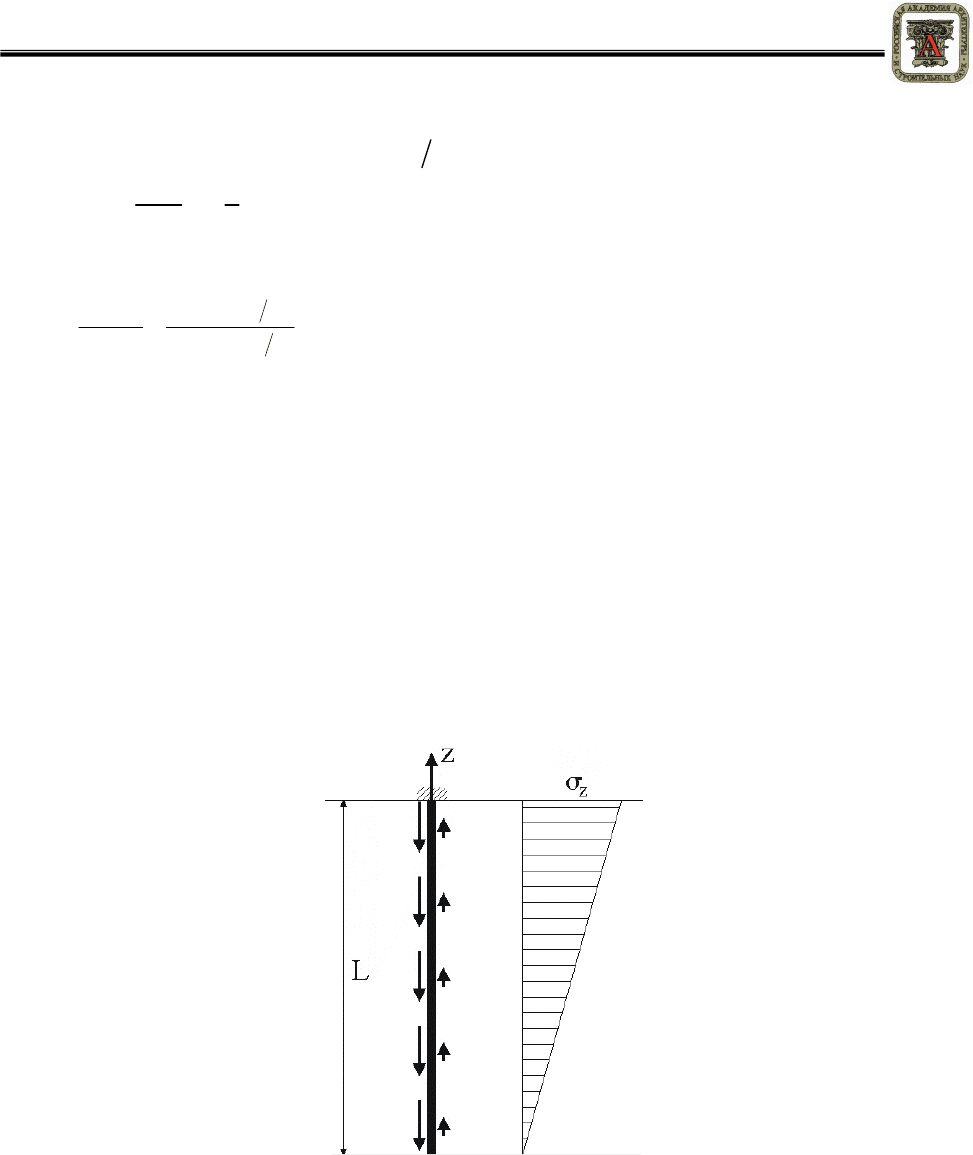
3.
Висячий
стержень
можно
рассматривать
как
волокно
полки
шириной
x,
к
сторонам
которого
приложены
касательные
напряжения
,
различные
слева
и
справа
за
счет
изменения
касательного
напряжения
в
поперечном
направлении
.
Рисунок 3 – Напряжения в «висячем Рисунок» стержне
В
точности
также
как
при
удлинении
висячего
стержня
и
неизменной
интенсивности
нагрузки
увеличиваются
нормальные
напряжения
в
заделке
,
так
и
при
изгибе
балки
в
сред
-
нем
по
длине
сечении
нормальные
напряжения
увеличиваются
при
увеличении
пролета
и
неизменных
перерезывающих
силах
.
Эти
две
задачи
не
похожие
и
не
аналогичные
–
это
одна
и
та
же
задача
.
Напряжения в местах пересечений полок и стенки
.
Заштрихованные
на
рисунках
1
и
2
области
полок
,
примыкающие
к
стенке
,
могут
быть
отнесены
как
к
полкам
,
так
и
к
стенке
.
Для
анализа
напряжений
в
этих
небольших
областях
целесообразно
проанализиро
-
вать
уравнения
равновесия
теории
упругости
,
считая
,
что
все
производные
от
напряжений
там
постоянны
.
xz1
τ
x S 2
=
xz1
b
Qb S
1
4W b
τ = −
(
)
( )
c
xz1
yz min b
A b 1 S b
0.30 0.03
2W 1 B 3
−
τ
= = ±
τ −
xz
τ
zx
τ
z
σ
xz
τ
∆
xz
τ
