Васин С.А., Ушакова И.В. и др. Основы черчения и начертательной геометрии

Подождите немного. Документ загружается.

Лекция № 19.

План:

19.1. Вращение вокруг оси, перпендикулярной плоскости проекций.

19.2. Плоскопараллельное движение.

19.1. Вращение вокруг оси, перпендикулярной плоскости проекций

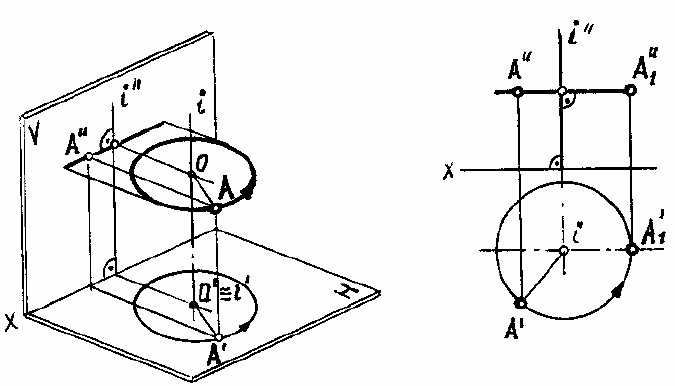
Правило: При вращении точки вокруг оси, перпендикулярной плоскости проек-

ций, одна ее проекция перемещается по окружности, а вторая – по прямой, перпендику-

лярной проекции оси вращения (рис. 106).

При вращении вокруг оси i, перпендикулярной H, точка А будет перемещаться по

окружности, расположенной в горизонтальной плоскости P. Эта окружность спроецирует-

ся на плоскость H в истинную величину, а на плоскость V – в отрезок прямой, располо-

женный на следе P

плоскости P (т.е. перпендикулярный i'').

Двойное вращение вокруг проецирующих осей приводит обычно к тому, что по-

следующие построения и новая проекция накладываются на заданную проекцию, что за-

трудняет чтение эпюра. Этого недостатка лишен способ плоскопараллельного перемеще-

ния.

Рис. 99

19.2. Плоско-параллельное движение

Плоско-параллельное движение (ППД) представляет собой вращение без указания

осей. На рис. 107 показано применение ППД для определения натуральной величины тре-

угольника АВС.

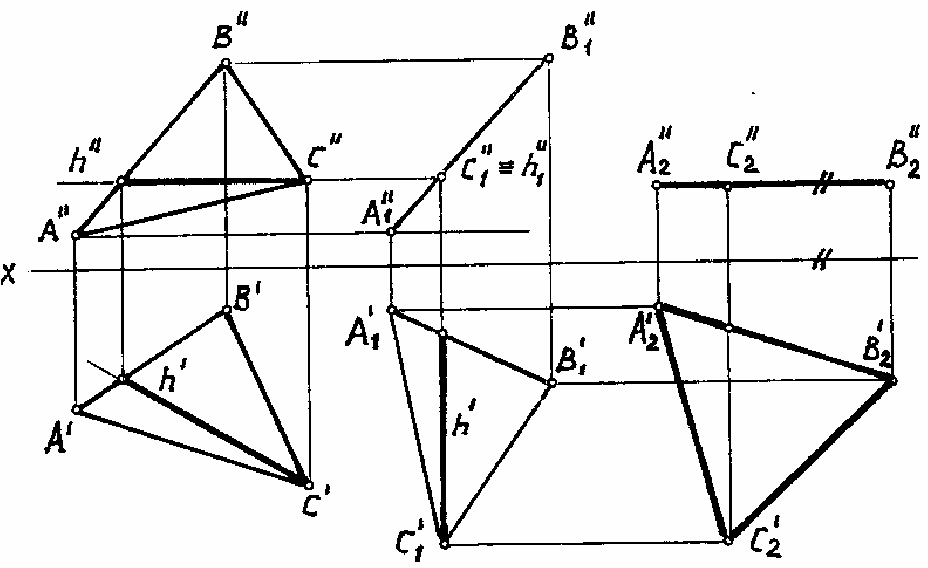
Рис. 100

ПЕРВЫМ ПОВОРОТОМ треугольник приведен в положение А

, перпендику-

лярное к плоскости H. Построение выполнено с помощью фронтали А

, которая вращени-

ем вокруг оси, перпендикулярной к плоскости V, расположена перпендикулярно к гори-

зонтальной плоскости проекций H (рис. 107).

Так как фронтальные проекции проецируемого объекта, вращаемого вокруг оси,

перпендикулярной к плоскости проекций V, не изменяют ни своей формы, ни величины,

фронтальная проекция А"В"С" отнесена параллельно самой себе на свободное место чер-

тежа (рис. 107).

Горизонтальная проекция А'B'C' получена путем проведения линий связи от фрон-

тальной проекции А"В"С" и переноса глубины (координата y) каждой вершины треуголь-

ника.

ВТОРЫМ ПОВОРОТОМ вокруг оси, перпендикулярной к плоскости H, А

приведен в положение А

, параллельное фронтальной плоскости V, при котором гори-

зонтальная проекция А'B'C' будет параллельна оси x.

Эта проекция отнесена на чертеже (рис. 107) вправо путем параллельного переме-

щения на удобное место. Проведя через точки А"

В"

С"

линии связи (перпендикулярно

оси x) и перенося высоты (координаты z) точек А, В, С, находим точки А'

В'

С'

Соединяя

эти точки последовательно прямыми, получим треугольник А”В”С”, являющийся нату-

ральной величиной треугольника АВС (рис. 107).

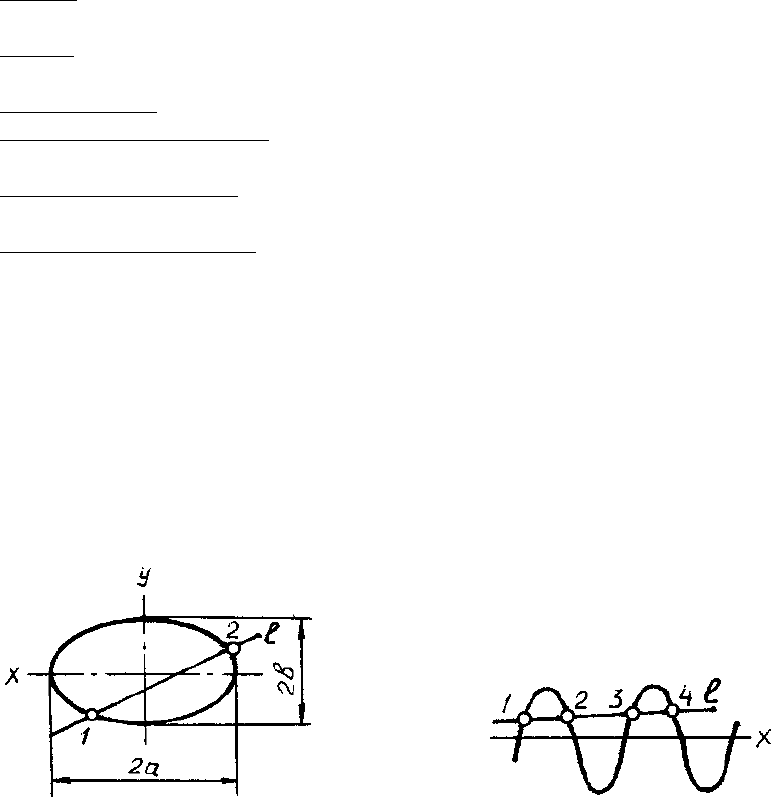
Лекция № 20.

ЛИНИИ И ПОВЕРХНОСТИ

План:

20.1. Линия

20.1.1. Винтовая линия

20.2. Поверхность

20.2.1. Поверхности линейчатые

20.2.2. Поверхности линейчатые развертывающиеся

20.2.3. Поверхности линейчатые неразвертывающиеся

20.2.4. Поверхности нелинейчатые

20.2.5. Поверхности параллельного переноса, вращения

20.1. ЛИНИЯ

ЛИНИЯ – это множество всех последовательных положений движущейся точки.

Евклид: “Линия же – длина без ширины”.

Прямая – разновидность линии, которая получается, если движущаяся точка не из-

меняет направления движения.

Кривая – разновидность линии, которая получается, если движущаяся точка изме-

няет направление движения.

Плоские линии – линии, все точки которых принадлежат одной плоскости.

Пространственные линии (линии двоякой кривизны) – линии, все точки которых не

принадлежат одной плоскости (например, линии пересечения поверхностей).

Алгебраические линии определяются алгебраическими уравнениями в декартовой

системе координат (окружность, эллипс, парабола, гипербола и др.).

Трансцендентные линии описываются трансцендентными уравнениями (синусои-

да, спираль Архимеда и др.).

Если алгебраическое уравнение линии n-й степени, то алгебраическая кривая счи-

тается n-го порядка, то есть ПОРЯДКОМ КРИВОЙ называют наибольшую степень ее

уравнения.

Геометрически порядок плоской кривой определяется наибольшим числом точек

ее пересечения с прямой, лежащей в плоскости кривой, а

для пространственной кривой –

пересечением ее с плоскостью.

Для алгебраических кривых это число точек всегда конечно. Для трансцендент-

ных – бесконечно. Например, для эллипса (рис. 108)

+ y

= 1

имеем n = 2, т.е. это – кривая второго порядка.

Рис. 101

Рис. 102

Для синусоиды (рис. 109) y = sin x имеем n = ∞.

Кривые бывают закономерные и незакономерные, как, например, горизонтали на

географической карте.

20.1.1. Винтовая линия

Пространственная кривая, широко применяемая в технике.

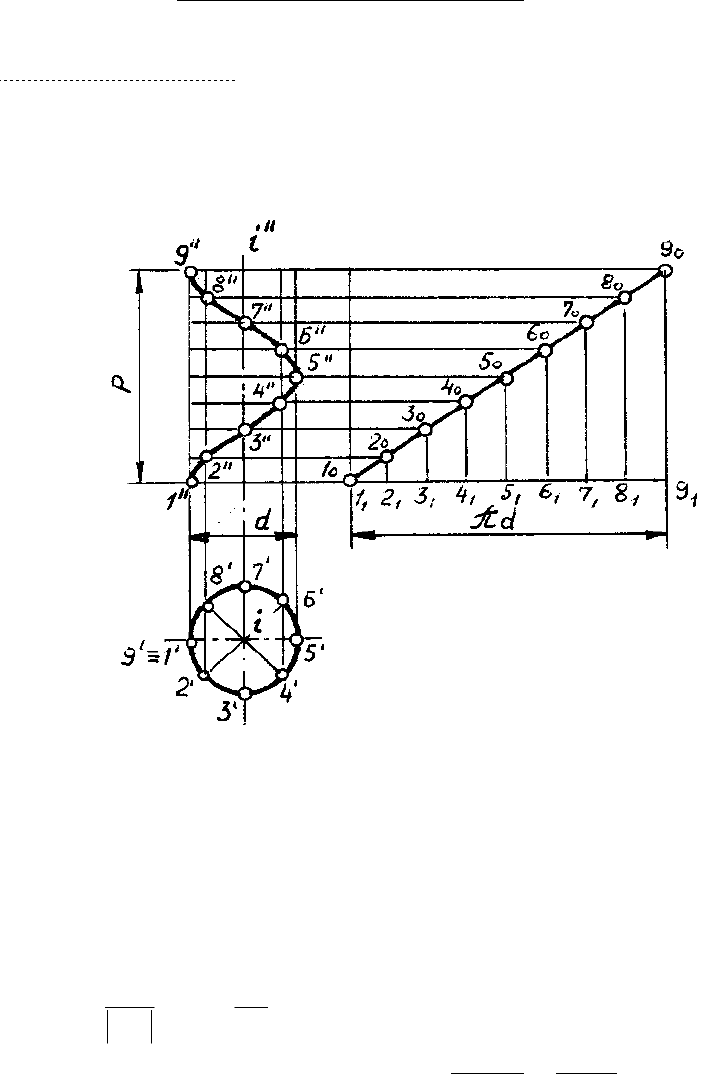
Цилиндрическая винтовая линия – пространственная кривая, получающаяся

в результате двойного равномерного движения точки: вращения вокруг оси и поступа-

тельного движения вдоль прямой, параллельной этой оси (рис. 110).

Рис. 103

p – шаг винтовой линии или расстояние между двумя ее соседними витками в на-

правлении, параллельном оси i. Шаг определяет величину перемещения точки в направ-

лении оси за один оборот этой точки вокруг оси.

Проекция цилиндрической винтовой линии на горизонтальную плоскость проек-

ций (при i ⊥ H) – окружность, на фронтальную плоскость проекций – синусоида.

Отрезок [1

] – развертка цилиндрической винтовой линии.

– угол подъема винтовой линии.

°= =arctg

arctg

101

Цилиндрические винтовые линии бывают правые

и левые. Основание для такого

деления – направление движения точки, спускающейся по винтовой линии. Если проекция

этого направления на плоскость, перпендикулярную к оси винтовой линии, совпадает с

направлением движения часовой стрелки – винтовая линия ПРАВАЯ. В противном слу-

чае – ЛЕВАЯ.

Коническая винтовая линия – пространственная кривая, получающаяся в ре-

зультате двойного равномерного движения точки: вращения вокруг оси и поступательного

движения вдоль прямой, пересекающейся с этой осью (рис. 111).

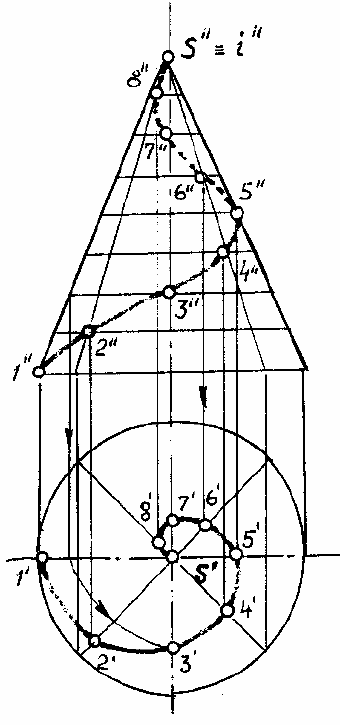
Рис. 104

При i ⊥ H горизонтальная проекция конической винтовой линии – архимедова спи-

раль, фронтальная – затухающая синусоида.

20.2. ПОВЕРХНОСТИ

С житейской точки зрения поверхность – внешняя сторона предметов. Так утвер-

ждают толковые словари. Евклид: “Поверхность есть то, что имеет только длину и шири-

ну”.

В технической практике принято рассматривать образование поверхности (как и

линии) с позиций кинематики – движения.

ПОВЕРХНОСТЬ – это множество последовательных положений движущейся ли-

нии – образующей.

Образующая может сохранять свою форму или изменять ее – деформироваться. За-

кон перемещения образующей определяется направляющими линиями, по которым сколь-

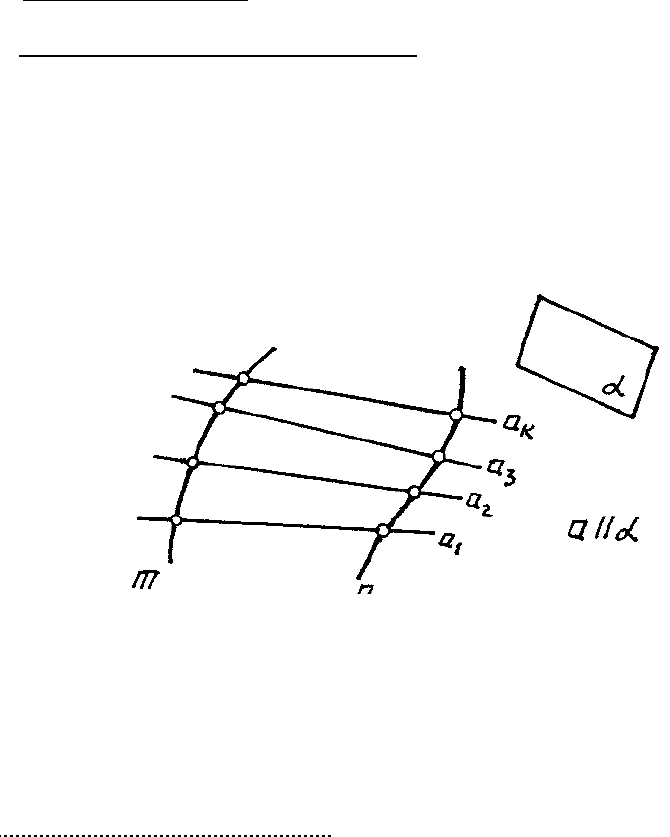
зит образующая и характером движения образующей. Например, поверхности Каталана

(названы так по имени бельгийского ученого, их исследовавшего), или – поверхности с

плоскостью параллелизма. Прямолинейная образующая “a” перемещается – скользит по

двум направляющим – “n” и “m”, оставаясь параллельной плоскости параллелизма α.

Для изображения поверхности на чертеже, используют КАРКАС – множество ли-

ний, заполняющих поверхность так, что через каждую точку поверхности проходит в об-

щем случае хотя бы одна линия каркаса. Проекции каркаса можно построить, если

извес-

тен определитель поверхности.

ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ – совокупность независимых усло-

вий, однозначно задающих поверхность.

Различают две части определителя:

– геометрическая часть указывает на геометрические фигуры (точки, линии, по-

верхности), с помощью которых образовывается поверхность; обозначается (Г);

– алгоритмическая (описательная) часть содержит указания о характере изменения

образующей и законе ее перемещения; обозначается [A].

Таким образом, определитель пишется в следующей форме:

Φ(Г)[A]

Определитель находят, исходя из кинематического способа образования поверхно-

сти. Например, для поверхностей Каталана:

Φ(m,n)[a || α]

Для задания этих поверхностей на эпюре Монжа достаточно указать проекции на-

правляющих m и n и положение плоскости параллелизма α (рис. 112).

Рис. 105

В геометрическую часть определителя не записывают образующую a. Поверхность

линейчатая (образующая – прямая линия). Поэтому априорно известно, что а – прямая.

В алгоритмической части содержится указание, что поверхность Каталана является

поверхностью с плоскостью параллелизма. Поэтому в геометрическую часть определите-

ля не записывают также и плоскость параллелизма.

20.2.1. Поверхности линейчатые

Линейчатые поверхности – поверхности, образующей которых является пря-

мая. Они могут быть развертывающиеся и неразвертывающиеся.

Развертывающиеся поверхности – поверхности, которые после разреза их,

например, по образующей, можно односторонне совместить с плоскостью без появления

разрывов и складок (рис. 113).

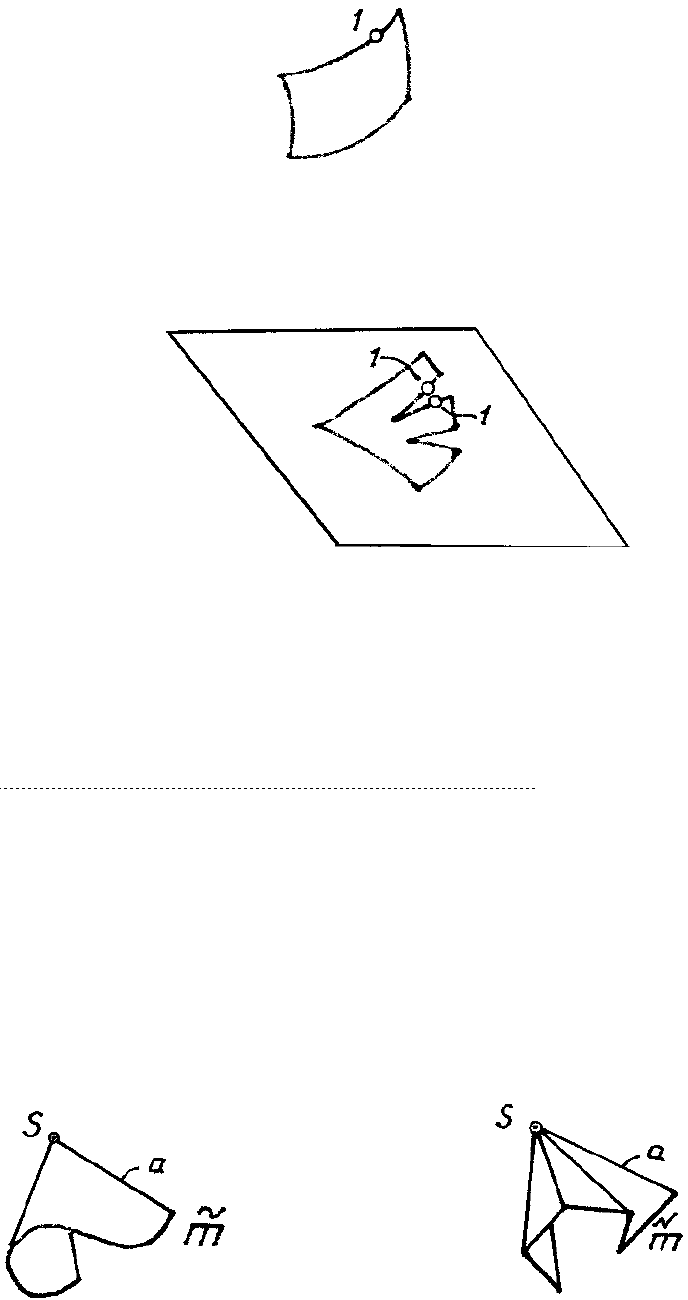
Рис. 106

Неразвертывающиеся поверхности – поверхности, которые нельзя совмес-

тить таким образом с плоскостью.

У развертывающихся поверхностей смежные образующие параллельны или пере-

секаются.

У неразвертывающихся поверхностей смежные образующие скрещиваются.

20.2.2. Поверхности линейчатые развертывающиеся

Эти поверхности делятся на три вида:

– с одной направляющей и вершиной в собственной точке;

– с одной направляющей и вершиной в несобственной точке;

– с ребром возврата (торсы).

К поверхностям с одной направляющей и вершиной в собственной точке относятся

коническая (направляющая – кривая) (рис. 114) и пирамидальная (направляющая –

ломаная) (рис. 115).

Определитель имеет

вид:

Φ(m)[(Sa ∈m);(a ∋S)],

причем “m” может быть соответственно

или

m .

Рис. 107

Рис. 108

К поверхностям с одной направляющей и вершиной в несобственной точке отно-

сятся цилиндрическая (направляющая – кривая) (рис. 116) и призматическая (направляю-

щая – ломаная) (рис. 117).

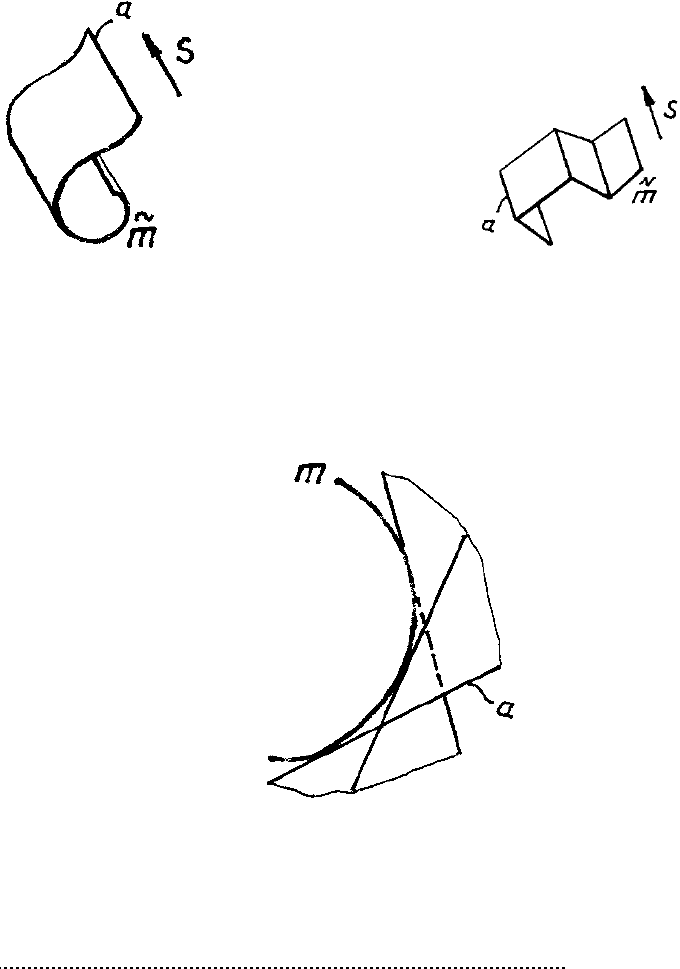
Рис. 109

Рис. 110

Определитель имеет вид:

Φ(m)[(S

∞

; (a || S)],

причем “m” может быть соответственно

или

m .

Поверхность с ребром возврата имеет одну направляющую – пространственную

кривую (ребро возврата). Образующая во всех своих положениях касательна к ребру воз-

врата (рис. 118).

Рис. 111

Определитель имеет вид:

Φ(m)[a U m]

20.2..3. Поверхности линейчатые неразвертывающиеся

Наиболее распространены в этой разновидности поверхностей поверхности Ката-

лана или поверхности с двумя направляющими и плоскостью параллелизма. Образующие

параллельны этой плоскости. Обычно принимают, что плоскости параллелизма совпадают

с одной из плоскостей проекций, т.е. α || H или α || V.

В числе поверхностей Каталана различают: цилиндроид, коноид и косую плоскость

или

гиперболический параболоид.

Цилиндроид образуется, когда обе направляющие – кривые. Его определитель

имеет вид:

Φ(

)[a || α]

Цилиндроид общего вида и пример применения этого вида поверхности для соеди-

нения двух трубопроводов одинакового диаметра, оси которых пересекаются под некото-

рым углом, показаны на рисунке 119 и рисунке 120.

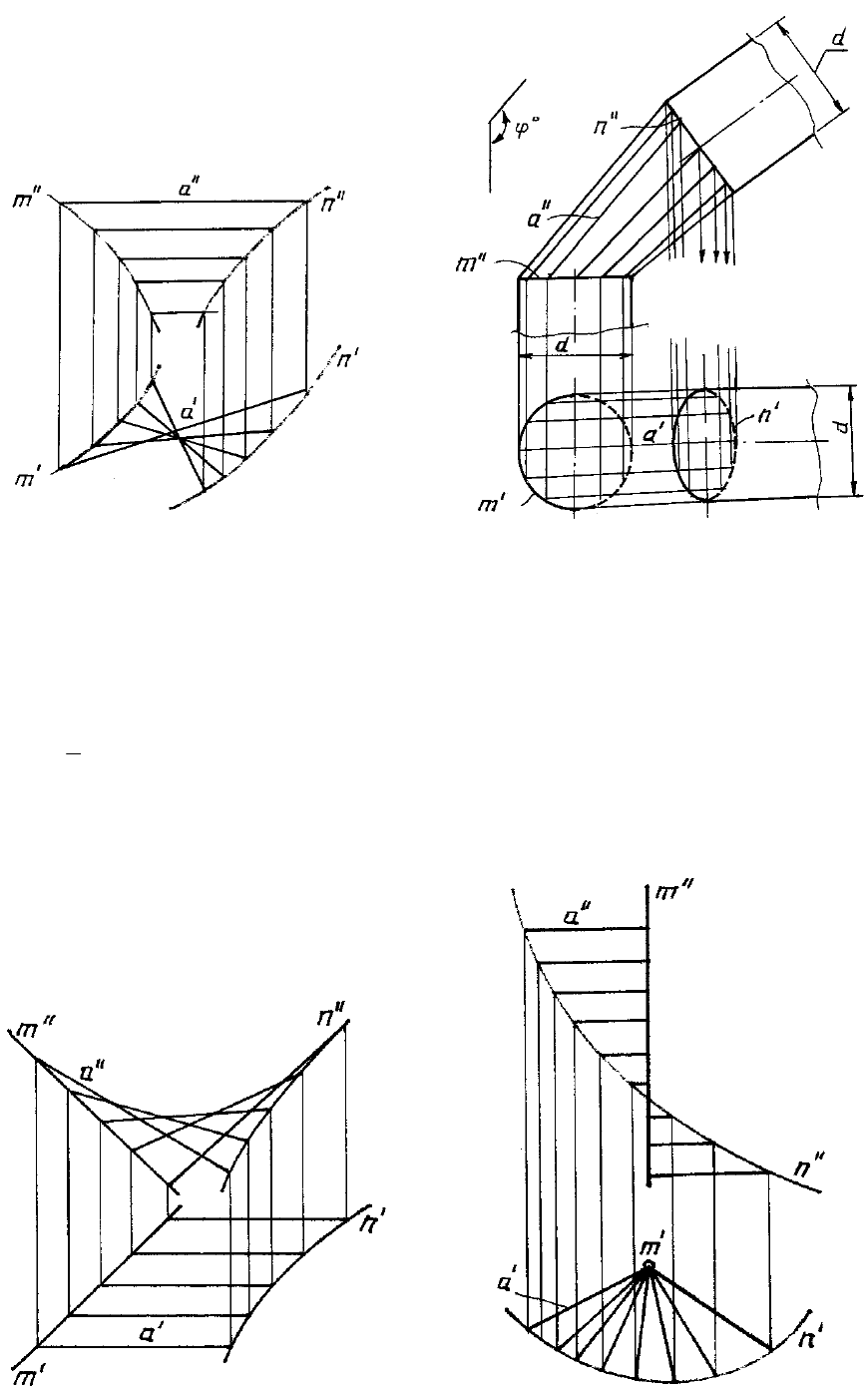
Рис. 112

Рис. 113

Для случая (рис. 119) определитель имеет вид:

Φ(

)[a || H]

Для случая (рис. 120) определитель имеет вид:

Φ(

)[a || V]

Коноид образуется, когда одна направляющая – прямая, другая – кривая. Опре-

делитель имеет вид:

Φ(

)[a || α]

На рисунках показаны коноид общего вида (рис. 121), коноид, у которого прямая

направляющая перпендикулярна плоскости параллелизма (прямой коноид) (рис. 122) и

аксонометрическая проекция, поясняющая происхождение названия “коноид”(рис. 123).

Рис. 114

Рис. 115

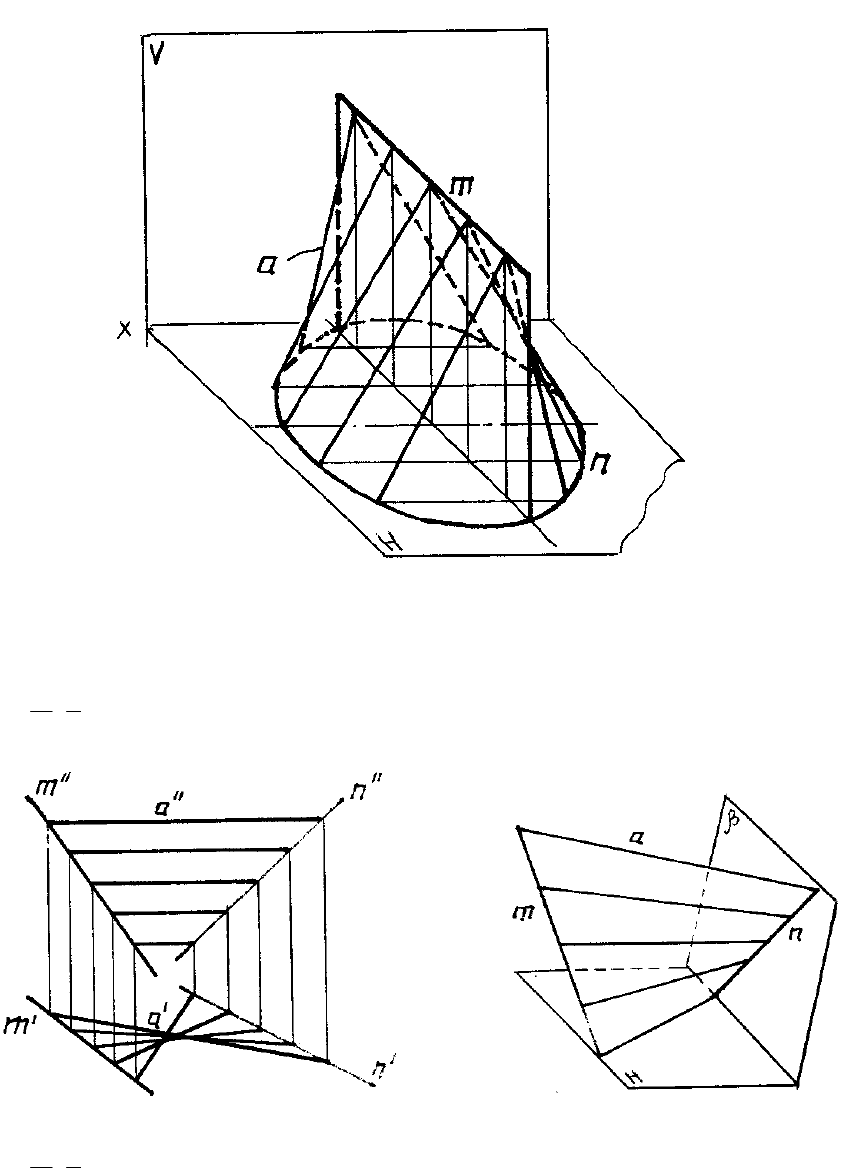
Рис. 116

Косая плоскость или гиперболический параболоид образуется, когда обе на-

правляющие – прямые (скрещивающиеся).

Для случая (рис. 124) определитель имеет вид:

Φ(

)[a || H]

Наглядное изображение косой плоскости показано на рис. 125.

Рис. 117

Рис. 118

Здесь a || H, то есть определитель имеет вид:

Φ(

)[a || H]

Наглядное изображение косой плоскости при a || V показано на рис. 126