Вакульчик В.С. Учебно-методический комплекс по высшей математике для студентов технических специальностей
Подождите немного. Документ загружается.

341
8)
2 2
sin44
2 2 180
π
°≈ − ⋅ .
Ответ
:
2
1
2
2 180
R
π
< ⋅
;
9)
1 1 1 1
1
2 4 2! 8 3!
e
≈ − + −
⋅ ⋅
.
Ответ
:
3
4
1
2 3!
R <
⋅
;
10)
3
1
sin2
90 90 3!
π π
°≈ − ⋅
.
Ответ
:
4
3
1
90 4!
R
π
< ⋅
;
11)
2
3
1 1 1
1
3
3 2!
e
≈ − +
⋅
.
Ответ
:
2
3
1
3 3!
R <
⋅
;
12)
arctg1,1 0,05
4
π
≈ − .
Ответ
:
1
0,04
R
<
Уровень II
Вычислите
приближенно
с
точностью
до
0,01:
1)
cos3
°
;
2)
ln0,9
;
3)
e
;
4)
3
127
;
5)
sin92
°
;
6)
3
e
;
7)
sin0,2
;
8)
4
83
;
9)
0,3
e
;
10)
8
;
11)
ln1,08
;
12)
5
31
;
13)
0,3
e
−
;
14)
cos0,1
;
15)
ln0,95
;
16)
cos85
°
.
Домашнее задание
1.
Разложите
функцию
arctg
y x
=
по
формуле
Тейлора
заданного
порядка
2
n
=
в
окрестности
точки
0
1
x
=
с
остаточным
членом
в
форме
Лагранжа
.
Ответ
:
( ) ( )
( )
2
2
1 1
4 2 4
x x
R x
− −
π
+ − +
.
2.
Разложите
функцию
2 1
x
y e
−
=
по
формуле
Тейлора
(n –
произволь
-
ный
порядок
)
в
окрестности
точки
0
1
2
x
=
с
остаточным
членом
в
форме
Пеано
.

342
3.
Разложите
функцию
(
)
2
1 sin
3
x
y x= −
по
формуле
Маклорена
(n –
произвольный
порядок
)
с
остаточным
членом
в
форме
Пеано
.
Ответ
:
( )
( )
( )
3 5 7 2 1
1
2 1
3 3 1
... 1 0
3
3 3! 3 5! 3 2 1 !
n
n
n
n
x x x x
x
n
+
−
+
−
− + − + − ⋅ +
⋅ ⋅ −
.
4.
Построить
график
функции
5 3
2 6 3
y x x
= − +
в
окрестности
точки
0
0
x
=
.
5.
Вычислите
предел
с
помощью
формулы
Тейлора
:
3 6
2 10
0
cos2 1 2
lim
4 4
x
x x
x x
→
− +
+
.
Ответ
:
1
6
.
Завершить выполнением внеаудиторной контрольной работы.
ВНЕАУДИТОРНАЯ КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ
«Дифференциальное исчисление функции одной переменной»
Вариант 0
1.
Найти
производные
следующих
функций
:
1.1.
5
lntg arctg2
x
y = .
( )
5
2
5 2 5 5
5
1 1 1 1
2 ln2 5
tg arctg2 cos arctg2 2 arctg2
1 2
x
x
x x x
x
y
′
= ⋅ ⋅ ⋅ ⋅ ⋅
+
;
1.2.
2
arccos
1
x
y
x
=
−
.
Применим
формулу
2
u u v uv
v
v
′
′ ′
−
=
,
тогда
( )
2
2 2
2
1 2
1 arccos
1 2 1
1
x
x
x x
x x
y
x
−
− ⋅ − − ⋅
− −
′
= =
−

343
( )
( )
2 2
2 2 3
2
1 arccos arccos 1
1 1
1
x x x x x x
x x
x
− − + ⋅ ⋅ − −
= =
− −
−
;
1.3.
2
2
arcsin
ln 1
1
x x
y x
x
= + −
−
.
2
2 2
2
2 2
2
arcsin 1 arcsin
1 2
1 2 1
1
1 2 1
x
x x
x x x x
x
x x
y
x
x x
−
+ − − ⋅ ⋅
−
− −
′
= + ⋅ =
−
− −
(
)
( )
( )
2 2 2
2
2 2 3
2
1 arcsin 1 arcsin
arcsin
1
1 1
1
x x x x x x
x x
x
x x
x
− + − + ⋅
= − =
−
− −
−
;
1.4.
arctg
x
xy
y
= .
Эта функция задана неявно. По правилу дифференцирования неяв-
ной функции получим
( )
(
)
( )
2 2
2 2
2 2
1
1
arctg
1
1
y x y
x y xy
xy y xy y
y
y
x x y
x
y
′
− −
′
−
′
′ ′
= ⇒ + = ⋅ ⇒ =
+ +
+
.
1.5.
( )
sin
cos
x
y x= .
Применение методов предварительного логарифмирования упрощает
вычисление производной сложно-показательной функции. Логарифмируя,
имеем
ln sin lncos
y x x
= ⋅
.
Дифференцируем обе части этого уравнения, не забывая что
(
)
,
y y x
=
( )
'
1 1
cos lncos sin sin
cos
y x x x x
y x
⋅ = ⋅ + ⋅ − .
Следовательно,
( ) ( ) ( )
2
sin sin
sin
cos cos lncos cos cos lncos tg sin
cos
x x
x
y x x x x x x x x
x
′
= ⋅ − = ⋅ −
.
2. Найти производные второго порядка:
2.1.
( )
2
arcsin
y x
= .

344
2
1
2arcsin ;
1
y x
x
′
= ⋅
−
2
2
2 2
2
1 1
2 1
2 arcsin
1
1 1
x
x
y x
x
x x
−
−
−
′′
= ⋅ + =
−
− −
( )
( )
2
2
2 2 3
2
1 arcsin 1 arcsin
2 2
1
1 1
1
x x x x x
x
x x
x
⋅ − + ⋅
= + =
−
− −
−
;
2.2.
ln ,
ln
.
x t t
y
t
y
t
= ⋅
=
=
Функция
задана
параметрически
,
следовательно
t
x
t
y
y
x
′
′
=
′
( )
( )
x
t
xx x
x
t
y
y y
x
′
′
′
′′ ′
= =
′
;
2 2
1
ln
1 ln
t
t t
t
t
y
t t
⋅ −
−
′
= = ;
1
ln ln 1
t
x t t t
t
′
= + ⋅ = +
;
( )
2
1 ln
1 ln
x
t
y
t t
−
′
=
+
;
( )
( ) ( ) ( )
( )
2 2
2
4
1 1
1 ln 1 ln 2 1 ln
1 ln
x
t
t t t t t t
t t
y
t t
− + − − + +
′
′
= =
+
(
)
(
)
(
)
( )
2
4
1 ln 1 ln 3 2ln
1 ln
t t t t t
t t
− + − − +
=
+
;
(
)
(
)
(
)
( )
3
4
1 ln 1 ln 3 2ln
1 ln
xx
t t t t t
y
t t
− + − − +
′′
=
+
.
3.
Найти
дифференциал
функции
:
3.1.
1
ln
1
x
y
x
−
=
+
.

345
( )
dy f x dx
′
=
2
2
1 (1 ) (1 ) 2
1
1
(1 )
1
x x
dy dx dx
x
x
x
x
− + − − −
= =
−
−
⋅ −
+
;
3.2.
3 2
,
x
y e
+
=
cos
x t
=
.
Учитывая
свойства
инвариантности
дифференциала
,
имеем
3 2 3cos 2
3( sin ) 3 sin
x t
dy e t dt e t dt
+ +
= ⋅ − = − ⋅
.
4.
Вычислим
приближенное
значение
sin 45
0
06′.
;
y dy
∆ ≈
( ) ( );
y f x x f x
∆ = +∆ −
( ) ( ) ( ) ; ( ) ( ) ( )
f x x f x f x x f x x f x f x x
′ ′
+∆ − ≈ ∆
⇒
+∆ ≈ + ∆
.
Эта
формула
дает
возможность
найти
значение
функции
( )
f x x
+∆
в
некоторой
точке
x x
+∆
,
если
известно
значение
функции
(
y f x
=
)
и
ее
производной
в
точке
x.
Вычислим
без
таблиц
sin 45
0
06′.
:
4
x
π
=
6
:
180 60 1800
x
π π
∆ = ⋅ =
( ) sin ;
f x x
=
( ) cos ;
f x x
′
=
2 2
sin sin cos 0,7083
4 1800 4 4 1800 2 2 1800
π π π π π π
+ ≈ + ⋅ = + ≈
.
5.
Показать
,
что
функция
3sin 4cos
y x x
= −
удовлетворяет
данно
-
му
уравнению
:
0
y y
′′
+ =
,
3cos 4cos
y x x
′
= +
;
3sin 4cos
y x x
′′
= − +
.
После
подстановки
в
уравнение
имеем
3sin 4cos 3sin 4cos 0; 0 0
x x x x
− + + − =
⇒
=
.
6.
Определить
наибольшее
и
наименьшее
значения
,
точки
перегиба
функции
изгибающего
момента
M(x) =
3 2
3 3 2
x x x
− + +
на
отрезке
[
]
2;2
−
.
1)
Функция
изгибающего
момента
М
(
х
)
на
данном
отрезке
дости
-
гает
своего
наибольшего
(
наименьшего
)
значения
или
в
критических
точ
-
ках
,
или
на
концах
этого
отрезка
346
2
( ) 3 6 3;
M x x x
′
= − +
[
]
( ) 0 1; 1 2;2
M x x x
′
=
⇒
= = ∈ −
,
(1) 3;
M
=
( 2) 24;
M
− = −
(2) 4
M
=
.
Сравнивая
значения
функции
в
этих
точках
,
заключаем
,
что
наимень
-
шее
значение
функции
m = – 24
достигается
при
х
= – 2 (
на
левом
конце
отрезка
),
а
наибольшее
–
М
= 4
в
точке
x = 2 (
на
правом
конце
отрезка
).
2)
Находим
точки
перегиба
( ) 6 6;
M x x
′′
= −
( ) 0 1
M x x
′′
=
⇒
=
(1 ) 0
M
′′
+ε >
(1 ) 0
M
′′
−ε <
.
Так
как
( )
M x
′′
при
переходе
через
х
= 1
меняет
знак
,
следовательно
,
х
= 1
является
точкой
перегиба
.
7.
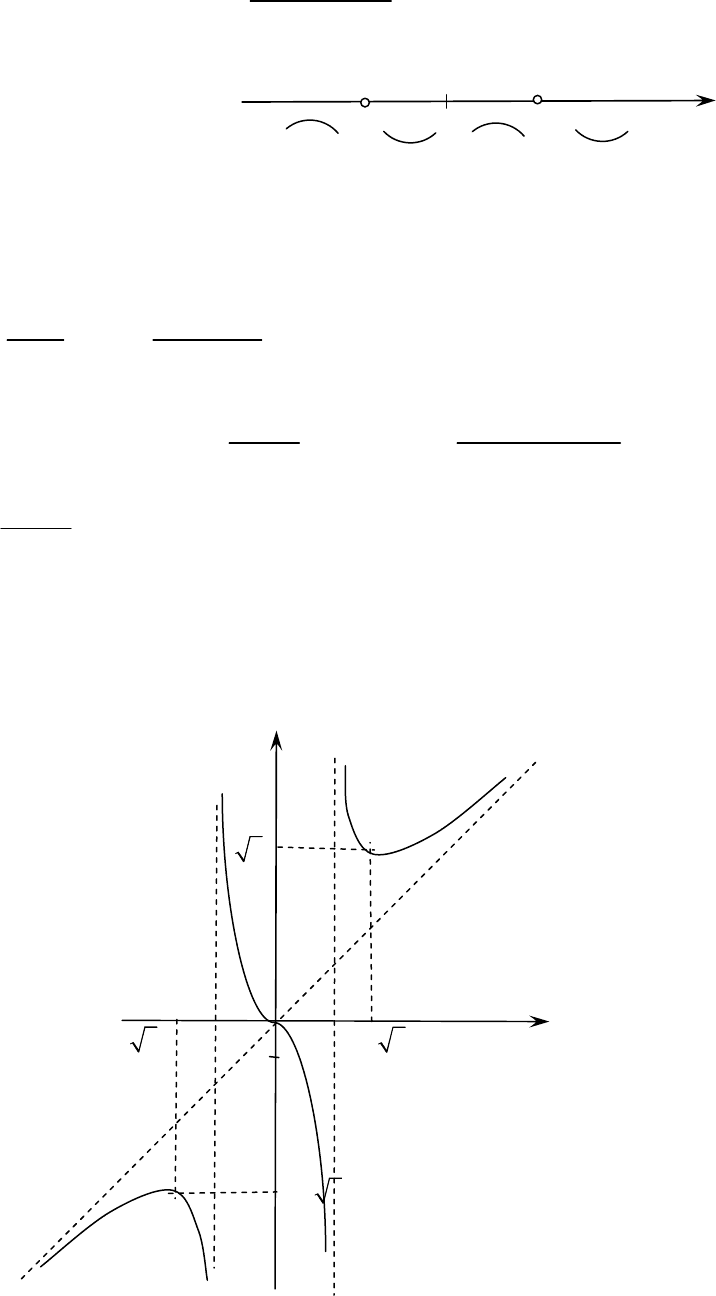
Исследовать
функцию
и
построить
ее
график
3
2
2
4
x
y
x
=
−
.
1)
( ) ( ; 2) ( 2;2) (2; ]
D y
= −∞ − ∪ − ∪ +∞
;
Прямые
2
x
= ±
являются
вертикальными
асимптотами
;
3
2
2 0
2
lim
4
x
x
x
→− −
= −∞
−
;
3
2
2 0
2
lim
4
x
x
x
→− −
= +∞
−
;
3
2
2 0
2
lim
4
x
x
x
→− −
= −∞
−
;
3
2
2 0
2
lim
4
x
x
x
→− −
= +∞
−
;
2)
функция
нечетная
,
график
симметричен
относительно
начала
ко
-
ординат
,
поэтому
исследование
функции
достаточно
провести
на
проме
-
жутке
[
]
0;
∞
.
Функция
не
периодична
;
3)
находим
первую
производную
( ) ( )
(
)
( )
2 2
2 2 3 4 2
2 2 2
2 2 2
2 12
6 ( 4) 2 2 2 24
4 4 4
x x
x x x x x x
y
x x x
−
− − ⋅ −
′
= = =
− − −
.
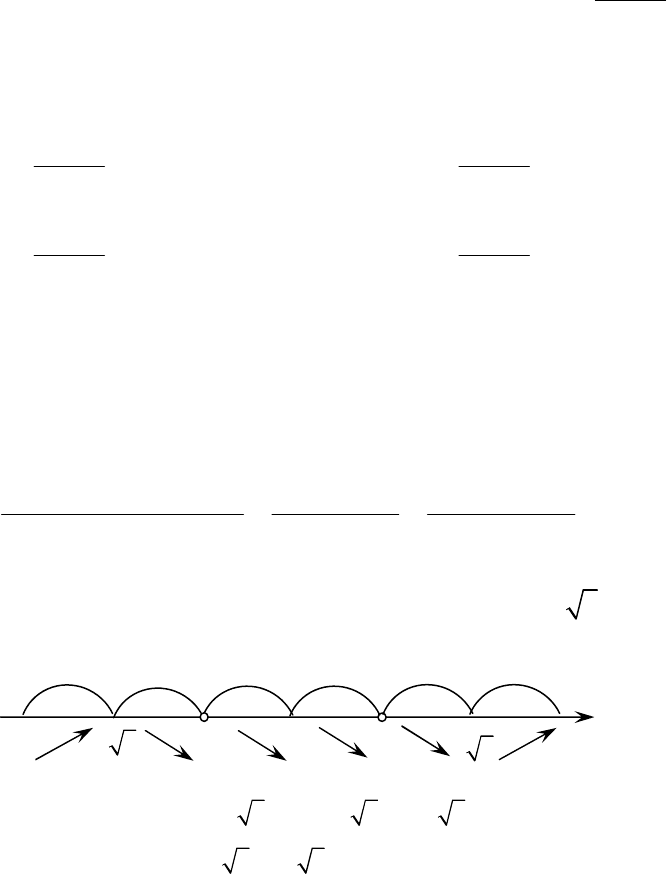
Критическими точками 1 рода будут
0, 2 3
x x= =± .
y
′
x
+
–
–
–
-
2 3
−
–2
0
(
)
(
)
max
2 3 2 3 6 3
y y− = − = −
,
(
)
min
2 3 6 3
y =
;
y
–
+
2
2 3
347
4) вторая производная
2
2 3
16 ( 12)
( 4)
x x
y
x
+
′′
=
−
дает критическую точку
второго рода х = 0.
5) находим наклонную асимптоту
y kx b
= +
( )
3
2
( ) 2
lim lim 2
4
x x
f x x
k
x
x x
→+∞ →+∞
= = =
−
;
3 3 3
2 2
2 2 2 8
lim ( ( ) ) lim 2 lim
4 4
x x x
x x x x
b f x kx x
x x
→+∞ →+∞ →+∞
− +
= − = − = =
− −
2
8
lim 0
4
x
x
x
→+∞
= =
−
.
При
x
→−∞
k и b принимают те же значения, следовательно, гра-
фик функции имеет наклонную асимптоту y = 2x;
6) график имеет одну точку пересечения с осями координат. Ис-
пользуя результаты исследования, строим график
–2
–1
2
y
x
0
6 3
−
2 3
2 3
−
6 3
+
2
–
x
–2
0
y
′
′
(
)
.
0 0
перег
y y
= =
– +
348
8. Пользуясь правилом Лопиталя, вычислить пределы:
8.1.
3
2arctg
lim
1
x
x
x
e
→+∞
π−
−
.
Это неопределенность типа
0
0
. Используя правило Лопиталя, получаем
2
2
3 3 3 2
2
2
2arctg 2 1 2
1
lim lim lim lim
3 3
1
3
1
x x x x
x x x
x x
x
x
e e e
x
→+∞ →+∞ →+∞ →+∞
−
π−
+
= = ⋅ =
+
− −
;
8.2.
(
)
1
ln 1
0
lim
x
e
x
x
−
→
.
Это неопределенность типа
(
)
0
0
. Логарифмируя предварительно
1
( 1)
x
e
y x
−
= , получаем равенство:
( )
1
ln ln
ln 1
x
y x
e
= ⋅
−
(неопределенность типа
∞
∞
).
Находим предел
ln
y
, после чего находим и предел y:
( )
0 0 0
1
ln 1
limln lim lim
ln 1
1
x
x x
x
x x x
x
x e
x
y
e x e
e
e
→ → →
−
= = = =
⋅
−
−
0 0 0
1 1
lim lim 1 lim 1
1
x x
x
x x x
e e
x
e
→ → →
−
= ⋅ = ⋅ =
,
следовательно
,
1
1
ln( 1)
0 0 0 0
limln 1 ln lim 1 lim lim
x
e
x x x x
y y y x e e
−
→ → → →
=
⇒
=
⇒
= = =
.

349
ГЛОССАРИЙ
Производная функ-
ции в точке x
0
предел
отношения
приращения
функции
∆y
к
приращению
аргумента
∆x
при
стремлении
∆x
к
нулю
:
( )
0
lim
x
y
y f x
x
→
∆
′ ′
= =
∆
Функция имеет
бесконечную произ-
водную,
если
для
некоторого
значения
x
выполняется
од
-
но
из
условий
0
lim
x
y
x
∆ →
∆
= +∞
∆
или
0
lim
x
y
x
∆ →
∆
= −∞
∆
Производной 2-го
порядка от функ-
ции
(
)
=
y f x
называется
производная
от
ее
первой
производ
-
ной
.
Обозначают
′′
y
,
( ) ( )
( )
′
′′ ′
=
f x f x
,
2
′′
x
y
Дифференциал
функции
(
)
=
y f x
в
точке x
0
произведение
производной
функции
(
)
0
′
f x
на
приращение
аргумента
∆x,
т
.
е
.
(
)
0
′
= ⋅∆
dy f x x
,
если
x –
независимая
переменная
,
то
(
)
0
′
= ⋅
dy f x dx
Геометрический
смысл дифферен-
циала заключается
в следующем
дифференциал
функции
(
)
=
y f x
в точке
x
0
ра
-
вен
приращению
ординаты
касательной
при
0
→
x x
Асимптота к гра-
фику функции
(
)
=
y f x
прямая
,
к
которой
приближается
точка
М
(x, y),
лежащая
на
графике
,
при
неограниченном
удале
-
нии
ее
от
начала
координат
;
асимптоты
бывают
наклонные
= +
y kx b
или
вер
-
тикальные
=
x a
,
или
горизонтальные
=
y b
.
Производной n-
ного порядка
от
функции
(
)
=
y f x
называется
производная
от
ее
производной
(n-1)-
го
порядка
.
Приняты
следующие
обозначения
( ) ( ) ( ) ( )
(
)
1
, , ,
III IY n n
y y y y
−
′
=
…
,
n
n
d y
dx

350
Свойство инвари-
антности (неиз-
менности) диффе-
ренциала первого
порядка)
Дифференциал
функции
равен
произведению
производной
на
дифференциал
аргумента
,
незави
-
симо
от
того
,
является
ли
этот
аргумент
независи
-
мой
переменной
или
функцией
другой
независи
-
мой
переменной
dy y dx
′
= ⋅
Точкой локального
минимума (макси-
мума) функции
(
)
=
y f x
является
точка
0
x
,
если
(
)
0 0
,x x x
∀ ∈ −δ +δ
вы
-
полняется
неравенство
(
)
(
)
0
f x f x
≥
,
(
)
(
)
(
)
0
f x f x
≤
.
Точкой перегиба
называется
точка
,
в
которой
функция
меняет
на
-
правление
выпуклости
Формула Тейлора
позволяет
приближать
некоторую
функцию
(
)
y y x
=
,
дифференцируемую
n
раз
,
к
многочле
-
нам
n-
ной
степени
:
(
)
(
)
(
)
n n
f x P x R x
= +
,
где
( )
( ) ( )( )
(
)
( )
0 0 0 0
...
!
n
n
n
y
P x y x y x x x x x
n
′
= + − + + −
Остаточным чле-
ном, записанным в
форме Пеано
называется
остаточный
член
( )
( )
(
)
0
0
n
n
R x x x= −
Остаточным чле-
ном, записанным в
форме Лагранжа
называется
остаточный
член
( )
(
)
(
)
( )
( )
1
1
0
1 !
n
n
n
y c
R x x x
n
+
+
= −
+
,
где
(
)
0
,
c x x
∈
