Вакульчик В.С. Учебно-методический комплекс по высшей математике для студентов технических специальностей
Подождите немного. Документ загружается.


301
Обучающая задача. Исследовать поведение функций в окрестно-
сти точки
0
0
x
=
:
1
0
.
2
cos
4
x
y x
= + .
Решение:
sin
2
x
y x
′
= − ⇒
⇒⇒
⇒
(
)
0 0
y
′
=
при
0
0
x
=
и
0
0
x
=
– критиче-
ская точка функции. Выяснить, меняет ли
y
′
знак в окрестности точки
0
0
x
=
, непросто. Поэтому исследуем поведение функции в этой точке с
помощью второй производной:
1
cos
2
y x
′′
= − ⇒
⇒⇒
⇒
( )
1 1
0 1 0
2 2
y
′′
= − = − <
.
Так как
(
)
0 0
y
′′
<
, то функция у в точке
0
0
x
=
имеет локальный
максимум:
( )
2
max
0
0 cos0 1
4
y
= + =
.
2
0
.
sin sh 2
y x x x
= + −
.
Решение:
(
)
cos ch 2
y x x x
′
= + −
⇒
(
)
0 1 1 2 0
y
′
= + − =
.
(
)
sin sh
y x x x
′′
= − +
⇒
(
)
0 sin0 sh0 0
y
′′
= − + =
.
Так как
(
)
0 0
y
′′
=
, то вычисляем
(
)
( )
0
n
y до первой производной, от-
личной от нуля:
(
)
ch cos
y x x x
′′′
= −
⇒
(
)
0 1 1 0
y
′′′
= − + =
;
(
)
( )
4
sh sin
y x x x
= + ⇒
(
)
( )
4
0 0 0 0
y
= + =
;
(
)
( )
5
ch cos
y x x x
= + ⇒
(
)
( )
5
0 1 1 2 0
y
= + = ≠
.
Первая, отличная от нуля производная – нечетного порядка (n = 5).
Следовательно,
0
0
x
=
– точка перегиба функции.
Преподаватель работает у доски со всей аудиторией.
Упражнение. Пусть
0
x
– критическая точка функции. При выпол-
нении каких из следующих условий функция в точке
0
x
будет иметь:
а) минимум; б) максимум; в) перегиб.

302
а)
(
)
( )
0
0
0,
0;
y x
y x
′′
=
′′′
>
б)
(
)
0
0
y x
′′
>
;
в)
( )
( )
( )
( )
0
0
4
0
0,
0,
0;
y x
y x
y x
′′
=
′′′
=
<
г)
(
)
0
0
y x
′′
<
;
д)
( )
( )
( )
( )
( )
( )
0
0
20
0
21
0
0,
0,
.................,
0,
0.
y x
y x
y x
y x
′′
=
′′′
=
=
<
Выполнить (самостоятельно, каждому свой вариант, два студен-
та у доски выполняют свои задания, по желанию третий уровень вы-
полняется у доски для получения оценки «10»).
Уровень I
Исследуйте поведение функции у в окрестности точки
0
x
:
1)
2
sin sh
y x x x
= − −
,
0
x
= 0; Ответ:
(
)
max
0 0
y
=
;
2)
(
)
2
2sin 1 3
y x x
= + + +
,
0
x
= – 1; Ответ:
(
)
min
1 4
y
− =
;
3)
2
arctg sh
y x x x
= + − ,
0
x
= 0; Ответ:
(
)
min
0 0
y
=
;
4)
2
1
x
y x e
−
= + −
,
0
x
= 2; Ответ:
(
)
min
2 2
y
=
;
5)
(
)
3
3 cos 1
y x x x
= − + −
,
0
x
= 1; Ответ:
(
)
max
1 3
y
=
;
6)
cos arctg
y x x x
= − −
,
0
x
= 0; Ответ:
(
)
min
0 1
y
= −
;
7)
2
1 ch cos
y x x x
= − − + ,
0
x
= 0; Ответ:
(
)
max
0 2
y
=
;
8)
2
sh
y x x x
= − −
,
0
x
= 0; Ответ:
(
)
max
0 0
y
=
;
9)
2
arctg2 1
x
y e x
= − +
,
0
x
= 0; Ответ:
(
)
min
0 2
y
=
;
10)
1
2
x
y x e
+
= − − ,
0
x
= – 1; Ответ:
(
)
max
1 4
y
− = −
;
11)
( )
2
sh 1
2
x
y x
= − −
,
0
x
= 1; Ответ:
(
)
max
1 0,5
y
= −
;
12)
2
ch cos 3
y x x x
= + + +
,
0
x
= 0; Ответ:
(
)
min
0 5
y
=
;
13) arctg
x
y x e
= −
,
0
x
= 0; Ответ:
(
)
max
0 1
y
= −
;
14)
3
4
3
x
x
y e x
= + − +
,
0
x
= 0; Ответ:
(
)
min
0 5
y
=
;
15)
(
)
2
2 sh 2
x
y e x
−
= + − −
,
0
x
= 2; Ответ:
(
)
min
2 3
y
=
.

303
Уровень III
Исследуйте поведение заданных функций в окрестности точки
0
x
.
1)
( )
2
1
0
, 0
, 0
0, 0
x
e x
y x x
x
−
≠
= =
=
;
2)
( )
2
1
0
, 0
, 0
0, 0
x
xe x
y x x
x
−
≠
= =
=
;
3)
( )
0
1
2 cos , 0
, 0
0, 0
x x
y x x
x
x
+ ≠
= =
=
.
Домашнее задание
1. Изучить тему «Вертикальные и наклонные асимптоты графика
функции. Общая схема исследования и построения графика функции».
2. C помощью производной первого порядка постройте графики
функций:
1)
3 2
16 12 4
y x x
= − −
.
2)
3
2
4 3
y x x
= + +
.
3. Найдите наибольшее и наименьшее значения функции
2
16
16
y x
x
= + −
на заданном отрезке [1; 4].
Ответ:
(
)
наим.
2 4
y y
= = −
;
(
)
наиб.
4 4
y y
= =
.
4. Найдите наибольшее и наименьшее значения функции
2sin sin2
y x x
= +
на заданном отрезке
3
0;
2
π
.
5. Исследуйте поведение функции
1
3
x
y e x
− +
= + +
в окрестности
точки
0
x
= 1.
Ответ:
(
)
min
1 5
y
=
.
6. Выполнить пятое и шестое задания из внеаудиторной контроль-
ной работы.

304
VIII. Вертикальные и наклонные асимптоты графика функции.
Общая схема исследования и построения графика функции
При изучении теории пределов мы уже проводили исследование
функции по упрощенной схеме и строили графики. Важным математиче-
ским инструментом для построения графика являются асимптоты. Напо-
минаем, что если хотя бы один из односторонних пределов
0 0
lim
x x
y
+
→
или
0 0
lim
x x
y
−
→
равен
∞
, то прямая
0
x x
=
является вертикальной асимптотой
графика. Если же
(
)
lim
x
y x A
→+∞
=
, то прямая у = А – горизонтальная асим-
птота графика при
x
→ +∞
(аналогично при
x
→−∞
). График функции
при
x
→ +∞
или
x
→−∞
может иметь наклонные асимптоты.
Преподаватель у доски выполняет со всей аудиторией.
Упражнение. Найдите
а) вертикальную, б) наклонную
асимптоты графика функции
2
2 1
x
y
x
+
= .
Полное исследование функции будем проводить по следующей схеме:
1. Найти область определения функции D(y).
2. Найти множество значений функции E(y) (если это возможно).
3. Выделить особенности функции (четность, нечетность, периодич-
ность). Если функция четная, исследование проводим для
0
x
≥
. Для не-
четной функции – также. Если функция периодическая, исследование про-
водится на основном периоде.
4. Исследовать поведение функции на концах интервалов из области
определения с помощью пределов. Сделать выводы о непрерывности функ-
ции, характере точек разрыва, вертикальных и горизонтальных асимптотах.
5. Найти промежутки монотонности, точки экстремума.
6. Найти промежутки выпуклости и вогнутости и точки перегиба.
7. Найти наклонные асимптоты.
8. Определить точки пересечения графика с осями координат, для
этого положить:
0
x
=
– точка пересечения с осью ординат,
0
y
=
– точка пересечения с осью абсцисс.
Наклонные асимптоты графика
(
)
y f x
=
при x →
→→
→ ±∞:
y kx b
= +
, где
(
)
lim
x
f x
k
x
→±∞
= ,
(
)
(
)
lim
x
b f x kx
→±∞
= −

305
9. Построить график.
10. Если есть необходимость, составить таблицу дополнительных
точек.
Обучающая задача. Исследовать функцию
2
1
1
x x
y
x
− +
=
−
и постро-
ить ее график.
Решение.
1.
(
)
(
)
(
)
;1 1;D f
= −∞ +∞
∪
.
2. Так как область определения функции не является симметричным
множеством, то функция не является ни четной, ни нечетной. Функция не
является также периодической.
3.
2 2
1
lim lim lim
1
x x x
x x x
x
x x
→±∞ →±∞ →±∞
− +
= = =±∞
−
. Таким образом, функция
горизонтальных асимптот не имеет.
Изучим поведение функции в окрестности точки
1
x
=
.
2
1 0
1 3
lim
1 0
x
x x
x
→ −
− +
= = −∞
− −
,
2
1 0
1 3
lim
1 0
x
x x
x
→ +
− +
= = +∞
− +
.
Значит,
1
x
=
– точка разрыва функции
⇒
прямая
1
x
=
– вертикальная
асимптота.
4. Находим критические точки.
( )
2 2
2
1 2
1
1
x x x x
y
x
x
′
− + −
′
= =
−
−
,
0
y
′
=
⇔
2
2 0
x x
− =
⇒
1
0
x
=
,
2
2
x
=
.
Заметим, что точка
1
x
=
, в которой
y
′
бесконечна, не является критиче-
ской точкой, так как
1
x
=
не входит в область определения.
x (–∞; 0) 0 (0; 1) (1; 2) 2 (2; +∞)
y
′
+ 0 – – 0 +
y
max
–1
min
3
y
'
x
+
–
+
–
-
0
1
2
(
)
max
0 1
y
= −
,
(
)
min
2 3
y
=

306
5. Вычисляем
y
′′
:
( )
( )( ) ( )
(
)
( ) ( )
2
2
2
2 4 3
2 2 1 2 1 2
2 2
1 1 1
x x x x x
x x
y
x x x
′
− − − − −
−
′′
= = =
− − −
.
Так как
0
y
′′
≠
, то график не имеет то-
чек перегиба. График выпуклый вверх на ин-
тервале ( – ∞; 1), вниз – на интервале
(1; + ∞).
6. Найдем наклонные асимптоты графика
y kx b
= +
:
( )
2 2
2
1 1
lim lim 1
1
x x
x x x x
k
x x
x x
→±∞ →±∞
− + − +
= = =
−
−
,
2
1 1
lim lim 0
1 1
x x
x x
b x
x x
→±∞ →±∞
− +
= − = =
− −
.
y x
=
– наклонная асимптота графика при
x
→±∞
.
7. Если
0
x
=
, то
1
y
= −
. Если
0
y
=
, то
2
1 0
x x
− + =
⇒
x
∈∅
(так
как дискриминант отрицательный). Следовательно, график имеет только
одну точку пересечения с осью Оу (0; – 1).
8. Учитывая полученные результаты, строим график функции.
+
1
–
x
1
1
–1
2
2
3
y
x
0

307
Выполнить (самостоятельно, каждому свой вариант, студент у
доски выполняет свое задание, по желанию третий уровень выполня-
ется для получения оценки «10»).
Уровень I
Исследуйте функцию
(
)
y f x
=
и постройте ее график:
1)
3
3 2
x
y
x
−
=
;
2)
3
2
32
x
y
x
−
=
;
3)
4
1
1
y
x
=
−
;
4)
( )
2
4
1
x
y
x
=
+
;
5)
3
2
1 2
x
y
x
−
=
;
6)
( )
2
2
1
x
y
x
−
=
;
7)
2
4 1
4
x x
y
x
− +
=
−
;
8)
2
3 3
1
x x
y
x
− +
=
−
;
9)
2
2
4
3
x
y
x
=
+
;
10)
2
4
2 3
y
x x
=
+ −
;
11)
4
3
3 1
x
y
x
+
=
;
12)
(
)
( )
2
8 1
1
x
y
x
−
=
+
;
13)
2
8
4
x
y
x
−
=
+
;
14)
3
2
4
x
y
x
−
=
;
15)
2
2
2
y
x x
=
+
;
16)
2
4
3 2
y
x x
=
+ −
.
Уровень II
Исследуйте функцию
(
)
y f x
=
и постройте ее график:
1)
( )
2
3
1
y x x
= −
;
2)
( )
2
3
1
y x x= −
;
3)
( )
2
3
6
y x x= +
;
4)
( )
2
3
4
y x x
= +
;
5)
( )
(
)
2
3
1 4 4
y x x x
= + − +
;
6)
(
)
( )
2
3
2 1 3
y x x x
= − + −
;
7)
( )
2
3
3
y x x
= −
;
8)
(
)
2
3
2 1
y x x x
= + + ;
9)
(
)
( )
2
3
6 9 1
y x x x
= − + +
;
10)
3
3 2
2
y x x x
= − +
;

308
11)
3
3 2
12 36
y x x x
= − +
;
12)
( )
2
3
2
y x x= −
;
13)
( )
(
)
2
3
3 6 6
y x x x
= + + +
;
14)
( )
(
)
2
3
4 4 4
y x x x
= − − − +
;
15)
( )
2
2
3
4 3
y x x= − + ;
16)
( ) ( )
2
3
2 3
y x x
=− − −
.
Уровень III
Исследуйте функцию
(
)
y f x
=
и постройте ее график:
1)
3
1
3
x
y x
x
= − +
+
;
2)
3
2
1
x
y
x
=
−
.
Обучающая задача. Исследовать функцию
(
)
3
2
x
y x e
−
= −
и по-
строить ее график.
Решение.
1.
(
)
(
)
;D f
= −∞ +∞
.
2.
(
)
(
)
3
2
x
y x x e
+
− = − − ⋅
⇒ функция ни четная, ни нечетная.
3. Так как функция у непрерывна при всех
x
∈
ℝ
, то ее график не
имеет вертикальных асимптот.
Вычислим
(
)
(
)
(
)
3
lim 2
x
x
x e
−
→−∞
− = −∞ +∞ =−∞
. Значит, на
−∞
функция
горизонтальных асимптот не имеет.
Вычислим
(
)
(
)
3
lim 2 0
x
x
x e
−
→+∞
− = +∞ ⋅ =
( )
( )
( )
( )
3
3
3
2 2
1
lim lim 0
x
x
x x
x
x x
e
e
e
−
−
→+∞ →+∞
−
′
− −
= = =
′
.
Значит, на
+∞
функция имеет горизонтальную асимптоту
0
y
=
.
4. Исследуем функцию на экстремум.
(
)
(
)
3 3 3
2 3
x x x
y e x e x e
− − −
′
= − − = −
,
0
y
′
=
⇒
3
x
=
.
x (– ∞; 3) 3 (3; +∞)
y′
+ 0 -
y
max
1
–
3
+
x
y
′
(
)
max
3 1
y
=
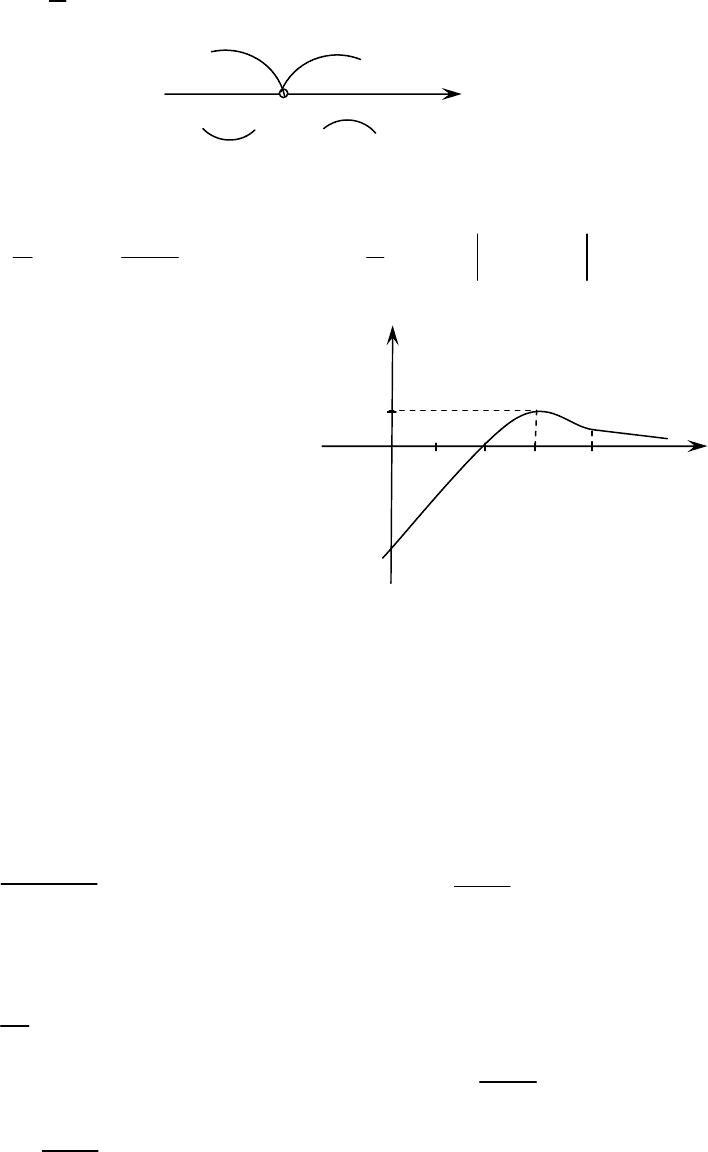
309
5. Находим точки перегиба:
(
)
(
)
3 3 3
3 4
x x x
y e x e x e
− − −
′′
= − − − = −
,
0
y
′′
=
⇒
4
x
=
;
(
)
1
4 2
y e
−
=
.
В точке
2
4;
e
график имеет перегиб.
6. Найдем наклонную асимптоту графика
y kx b
= +
при х→ – ∞.
3 3
2 2
lim lim lim 1
x x
x x x
y x
k e e e
x x x
− − +∞
→−∞ →−∞ →−∞
−
= = = − = = +∞ = +∞
⇒
наклонной асимптоты при х→ – ∞
график не имеет.
7.
0
x
=
⇒
3
2
y e
= −
; y = 0 ⇒
x = 2. График имеет две точки пересе-
чения с осями: А(0; –
3
2
e
−
), В(2; 0).
8. Строим график функции.
Выполнить (самостоятельно, каждому свой вариант, студент у
доски выполняет свое задание, по желанию третий уровень выполня-
ется для получения оценки «10»).
Уровень I
Исследуйте функцию
(
)
y f x
=
и постройте ее график:
1)
(
)
( )
2 2
2 2
x
e
y
x
+
=
+
;
2)
( )
(
)
2 1
2 1
x
y x e
−
= − ⋅
;
3)
x
e
y
x
=
;
4)
(
)
3
4
x
y x e
−
= −
;
5)
3
2ln 3
x
y
x
+
= −
;
6)
3
3
x
e
y
x
+
=
+
;
7)
(
)
2
1
x
y x e
+
=− +
;
8)
( )
(
)
2 1
2 3
x
y x e
− +
= +
;
9)
6
ln 1
x
y
x
+
= −
;
10)
2
x
y x e
−
=
;
+
4
–
x
y
′′
4
y
x
0
1
1
2 3

310
11)
(
)
2
3
x
y x e
−
= −
;
12)
1
2
1
x
e
y
x
−
= ⋅
−
;
13)
ln 3
2
x
y
x
= +
−
;
14)
( )
(
)
2 1
2 1
x
y x e
+
= − +
;
15)
2
2
x
e
y
x
−
=
−
;
16)
ln 1
5
x
y
x
= −
+
.
Уровень II
Исследуйте функцию
(
)
y f x
=
и постройте ее график.
1)
(
)
ln cos sin
y x x
= +
;
2)
1
sin cos
y
x x
=
+
;
3)
(
)
ln 2cos
y x
= −
;
4)
arctgcos
y x
=−
;
5)
(
)
ln sin cos
y x x
= −
;
6)
2sin
x
y e
−
=
;
7)
1
sin cos
y
x x
=
−
;
8)
3
sin
y x
=
;
9)
(
)
ln 2sin
y x
= −
;
10)
sin cos
x x
y e
+
=
;
11)
(
)
ln sin cos
y x x
= − −
;
12)
( )
2
1
sin cos
y
x x
=
−
;
13)
cos sin
x x
y e
−
=
;
14)
(
)
ln cos sin
y x x
= −
;
15)
arctgsin
y x
=
;
16)
sin cos
arctg
2
x x
y
+
=
.
Уровень III
Исследуйте функцию
(
)
y f x
=
и постройте ее график:
1)
2 2
sin
x
y e x
−
= ⋅
;
2)
2
2
1
arccos
1
x
y
x
−
=
+
.
Домашнее задание
1. Изучить тему «Физические и механические приложения диффе-
ренциального исчисления».
2. Построить графики функций своего варианта из внеаудиторной
контрольной работы.
