Удут Л.С., Кояин Н.В., Мальцева О.П. Проектирование и исследование автоматизированных электроприводов. Часть 1. Введение в технику регулирования линейных систем Часть 2. Оптимизация контура регулирования
Подождите немного. Документ загружается.

Ta
a
T
к
к
к
2
4
1
0
2
– частота колебаний,
с
рад
;
к
к
ee
a
a
4
1
1
2
– первое перерегулирование, о.е.;
1
)0(
1
1
ln
1
1
arctg
ру
t
– время первого достижения установившегося
значения, с;
к
рум
t
– время достижения максимума, с;
i
itt
1
ln
1
ln
)1(
)5(
2
рум
ру
– время переходного процесса (окончательного вхождения в зону
), с.
Здесь
i
– последний экстремум перерегулирования или провала перед
вхождением в зону
. Значения зоны
и экстремума
перерегулирования
i
берутся в относительных единицах. Каждое
последующее перерегулирование или провал (см. рис. 2.31, в) связано с
предыдущем соотношением
2
1
1
ln
i
i
.
Для системы типа “1–2” могут быть найдены выражения,
однозначно связывающие параметры переходной функции и частотных
характеристик. Частота колебаний
к
связана с частотой среза системы
cр
соотношениями:
2
)4(
кк
ср
к
aa
для
41
к
a
, где
Ta
к
cр
1
;
2
4
к
ср
к
a
для
10
к
a
, где
Ta
к
cр
1
.
При
0 2 0 707 a
к
( . )
амплитудная частотная характеристика
замкнутой системы на резонансной частоте (см. рис. 2.31, б)
222
2
р
2
2
4
21
Ta
a
T
к
к
имеет явно выраженный резонансный максимум и характеризуется
показателем колебательности
)4(
2
)1(2
1
22
кк
aa
M
,
что приводит к существенному перерегулированию (более 5 %)
1
1
2
MM
e
.
132
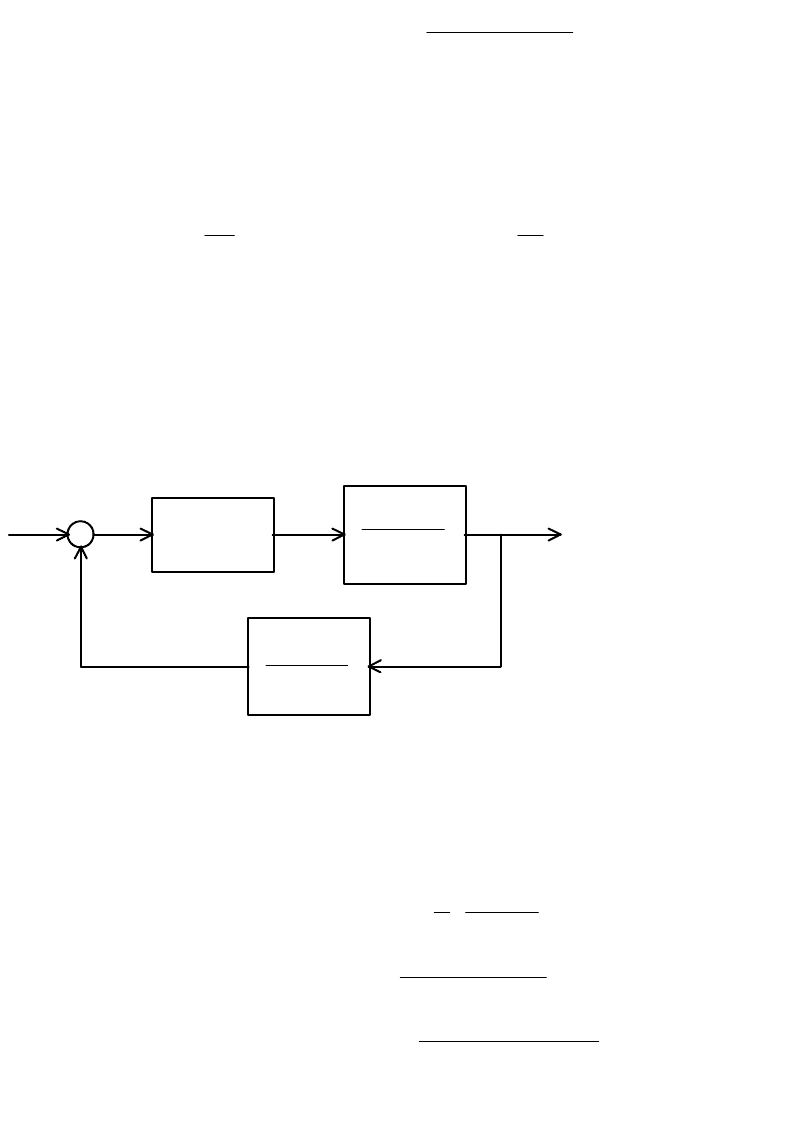
В заключение остановимся на случае, когда передаточная функция
оптимизированного контура второго порядка не приводится к
стандартному виду (2.19), а имеет (см. пример 2.12) в общем случае вид
.
1
1
)(
1
2
2
1
papa
pb
pW
з
(2.68)
При выполнении для передаточной функции (2.68) условия
оптимизации
2
2
1
2a a
(2.69)
показатели работы контура будут зависить от отношения
коэффициентов
1
1
a
b
и уже при значении
6.0
1
1
a
b
перерегулирование в
контуре в режиме отработки скачка задания будет превышать 5 %.
Пример 2.12. Оптимизировать контур, объект управления
которого (рис. 2.34) содержит инерционное звено с малой постоянной
времени
2
T
, а в цепи обратной связи имеется сглаживающий фильтр с
постоянной времени
0
T
.
Рис. 2.34
Принимаем ПИ-регулятор с передаточной функцией
,
1
1
)(
1
0
pT
pT
k
pW
рег
тогда
,
)1(
1
)(
21
pTpT
pW
p
1
1
)(
1
2
21
0
pTpTT
pT
pW
з
(2.70)
и согласно (2.69) условие оптимизации контура имеет вид:
10
TT
;
12
5.0 TT
.
Рассмотрим возможности других настроек при оптимизации
контура 2-го порядка с передаточной функцией вида (2.70).
W p
егр
( )
k
T p
2
1
1
1
0
T p
(-)
U
ос
U
з
y
133
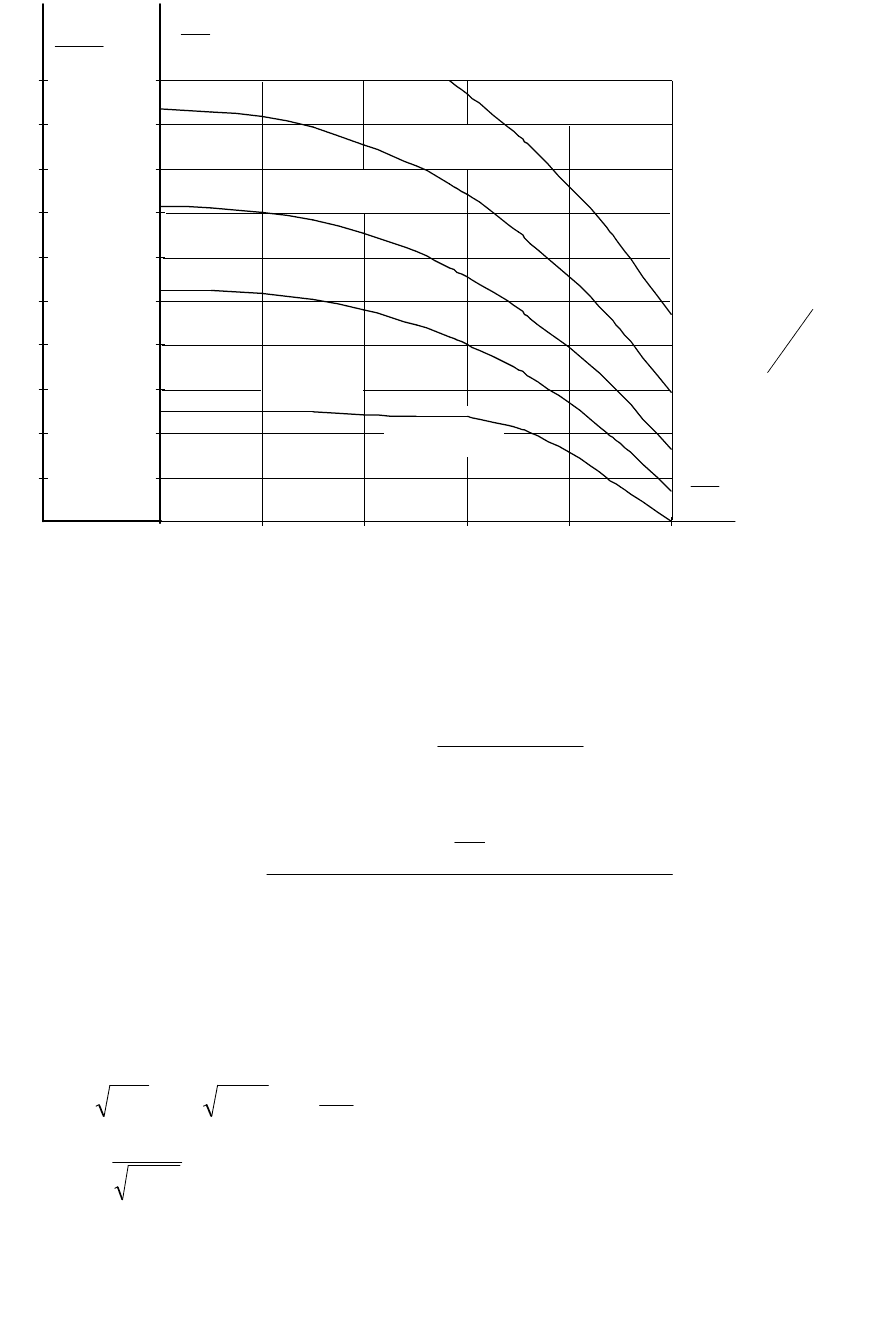
На рис. 2.35 для случая отработки ступенчатого входного
воздействия приведены зависимости перерегулирования
и
относительного времени первого вхождения в 5%-ю зону
1
)5(
1
T
t
ру
от
отношения параметров
1
0
T
T
, снятые при постоянных значениях
отношения
1
2
T
T
. На основании приведенных зависимостей делаем
следующие выводы:
1. Наименьшее быстродействие и перерегулирование
достигается при
.0
1
0
T
T
Следует отметить, что именно этот случай
соответствует настройке контура с передаточной функцией вида (2.19)
на МО.
2. Максимальное быстродействие и перерегулирование
достигается при
.1
1
0
T
T
3. При
4.0
1
0
T
T
максимальное быстродействие при
перерегулировании не более 6 % достигается при
5.0
1
2
T
T
.
4. При
4.0
1
0
T
T
максимальное быстродействие достигается при
выборе минимального значения отношения
5.0
1
2
T
T
.
134
5
10
15
20
25
30
%
0.2 0.4 0.6 0.8 1
T
T
0
1
T
T
2
1
=1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
t
T
ур
( )
1
5
1
1
2
3
о.е.
2.5
1.5
0.5
1
T
T
2
=1
0.9
0.8
0.7
0.6
0.5
о.е.
0.4
0.3
0.2
0.1
f
T
T
( )
0
1
t
T
f
T
T
ур
( )
( )
1
5
1
0
1
Рис. 2.35
На рис. 2.36 в плоскости относительных значений параметров
1
0
T
T
и
1
2
T
T
приведены линии постоянного значения перерегулирования
и
здесь же соответствующие им зависимости времени переходного
процесса в о. е.
1
)5(
2
T
t
ру
в функции отношения параметров
1
0
T
T
.
Приведенные на рис. 2.35 и 2.36 результаты исследований
позволяют выбрать настройку контура 2-го порядка с передаточной
функцией вида (2.70), обеспечивающую максимальное быстродействие
при заданном перерегулировании.
135
0.2 0.4 0.6 0.8 1 о. е.
T
T
0
1
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
о. е.
T
T
2
1
t
T
ур
( )
2
5
1
о. е.
10
9
8
7
6
5
4
3
2
1
t
T
ур
( )
2
5
1
)0( %
)5( %
0 %
5 %
)10( %
)15( %
)20( %
10 %
15 %
20 %
Рис. 2.36
Контур третьего порядка. Передаточная функция для
замкнутого контура, оптимизированного по МО или СО с
дополнительным сглаживающим фильтром на входе контура
1
1
)(
pTba
pW
кк
вх.ф
, (2.71)
имеет вид
1
1
)(
222332
pTbapTbapTba
k
pW
кккккк
ос
з
.
Характеристическое уравнение замкнутого контура и его запись в
нормализованном виде по Вышнеградскому (см. п. 1.4.1. раздел 1),
соответственно, имеют вид:
;01
222332
pTbapTbapTba
кккккк
01
23
BqAqq
,
где
0
3
2
3
2
,,
p
qbaBbaA
ккк
;
3
2
0
1
Ta
к
– среднегеометрический корень.
Для решения задачи выбора параметров настройки контура,
отличной от типовой по МО или СО, построим диаграмму качества
Вышнеградского, но не в плоскости коэффициентов А и В, а в плоскости
коэффициентов настройки контура
к
a
и
к
b
.
136

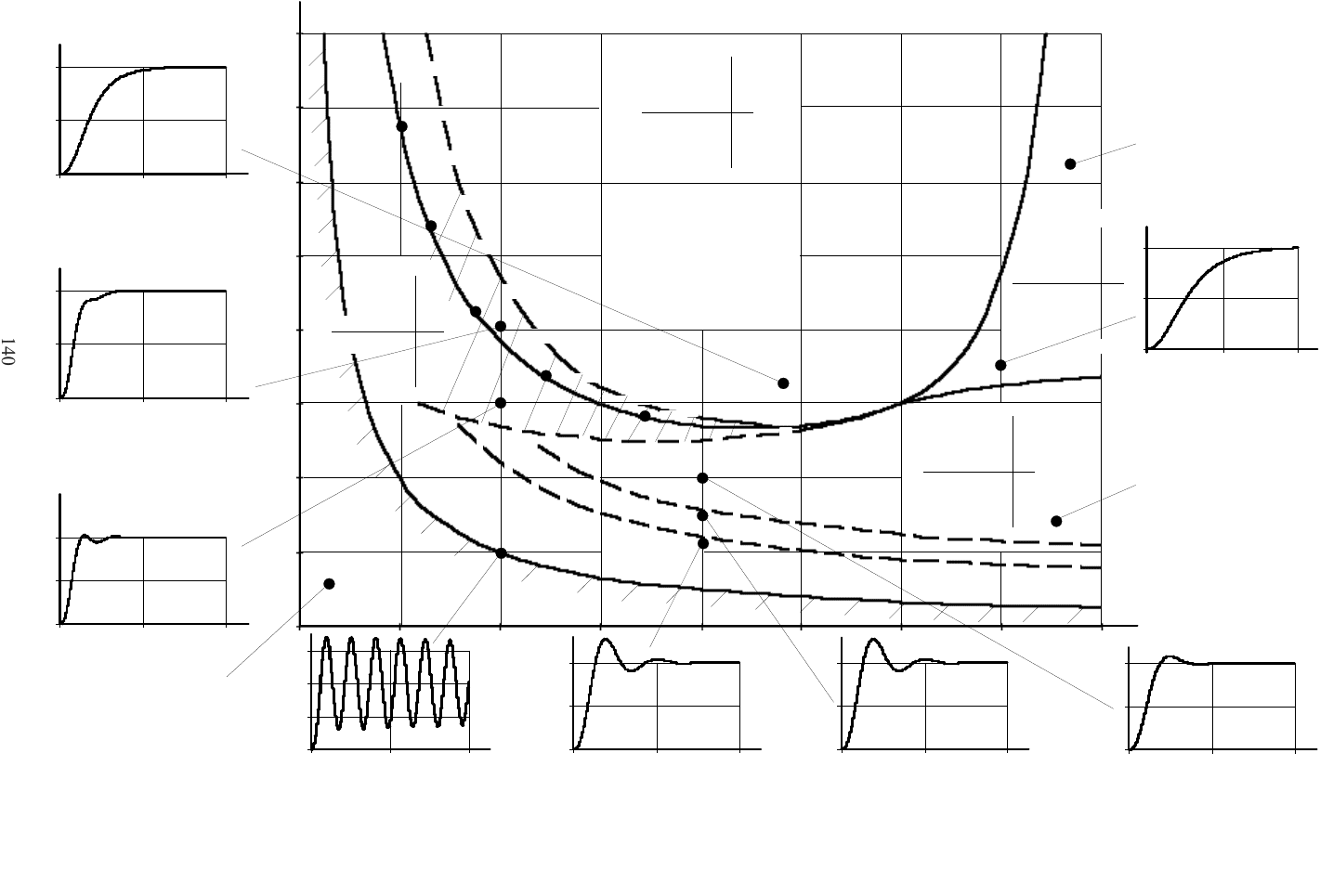
Уже отмечалось, что характер переходного процесса в замкнутой
системе, а следовательно, и качественные показатели, полностью
определяются расположением корней на комплексной плоскости. В
системе третьего порядка возможны два варианта распределения
корней: все три корня вещественные; один корень вещественный и пара
корней комплексных сопряженных. Поэтому в плане решения
поставленной задачи прежде всего выделим в плоскости параметров
к
a
и
к
b
область неустойчивости с положительной вещественной частью
комплексных сопряженных корней и область устойчивости. Границей
между областями является гипербола
1
кк
ba
, характеризующаяся
наличием пары чисто мнимых корней (кривая АВ рис. 2.37). Область
устойчивости находится выше границы и, в свою очередь, может быть
разбита на три области:
• область, где все три корня вещественные. Граница области
находится приравниванием нулю дискриминанта формулы Кардана
027184
2222
кккккккк
babababa
,
откуда
кк
кккккк
к
aa
aaaaaa
b
42
4274418418
2
222
2,1
.
Область вещественных корней ограничена кривыми CE и CF.
Переходный процесс в области определяется тремя
экспоненциальными составляющими;
• область, где вещественный корень лежит ближе к мнимой оси,
чем пара комплексных корней. Переходный процесс определяется
главным образом экспоненциальной составляющей, т. к. колебательная
составляющая затухает быстрее;
• область, где ближе к мнимой оси расположена пара
комплексных сопряженных корней, в результате чего экспоненциальная
составляющая затухает быстрее колебательной и переходный процесс
носит явно выраженный колебательный характер.
Границей между областями является кривая CD, которая
соответствует расположению всех трех корней на одинаковом
расстоянии от мнимой оси и находится на основании уравнения
02792
2
кккк
baba
.
137
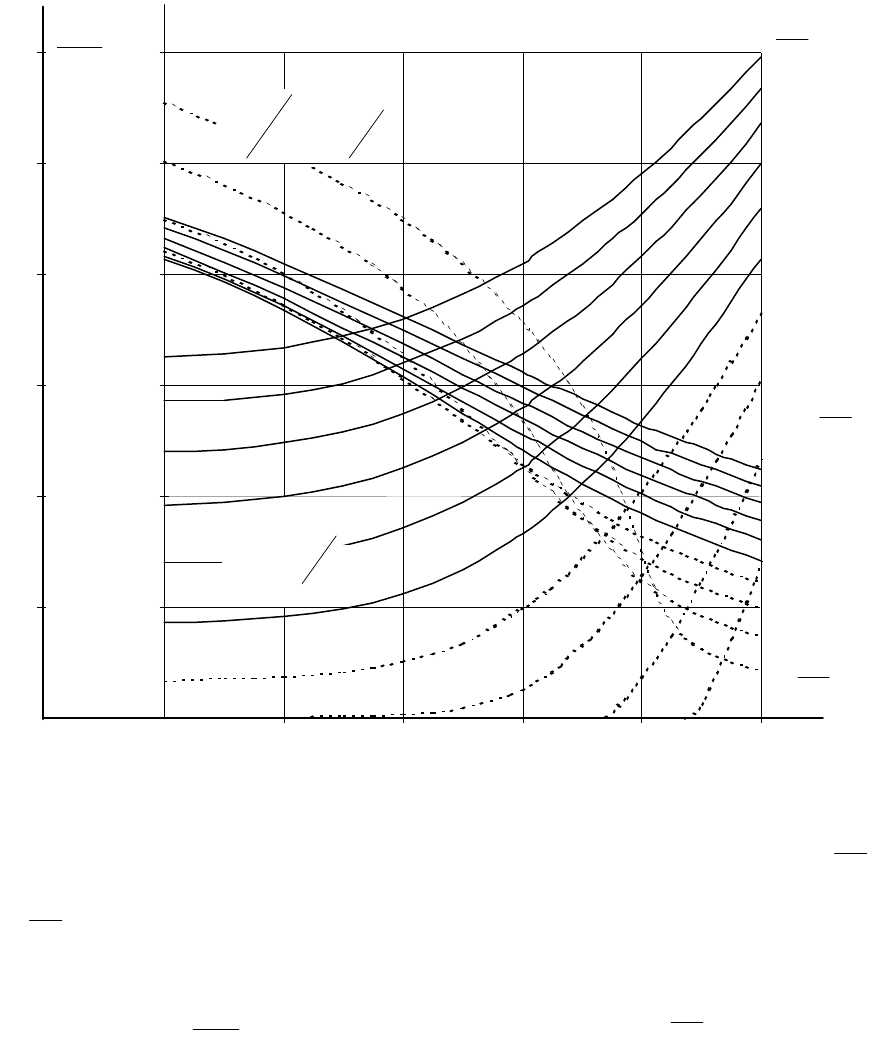
1
2
3
4
5
6
7
8
1 2 3 4
a
к
b
к
j
x
x
x
j
xx x
j
x
x
x
j
x
x
y
t
y
t
t
y
t
y
y
t
t
y
Область
монотонных
процессов
x
Область
колебательных
процессов
Область
неустойчивости
Область
апериодических
процессов
монотонных
F
III
III
IV
V
VI
VII
A
B D G
C
F
E
1
2
3
4
5
t
y
y
t
%5
2
%5
3
Рис. 2.37. Распределение корней и характер переходных процессов в системе третьего порядка
138

Таким образом, переходные процессы в контуре при ступенчатом
входном воздействии можно разделить на две группы: монотонные и
колебательные.
Монотонные переходные процессы – процессы, у которых первая
производная
)(ty
выходной координаты не меняет знак в течение
всего времени регулирования, т. е.
0
)(
t
ty
d
d
при
р
tt 0
[6]. В
плоскости параметров
к
a
и
к
b
(рис. 2.37) монотонные процессы имеют
место выше кривой GCF (области I и II). Среди монотонных
переходных процессов можно выделить монотонные апериодические
(область I).
Колебательные переходные процессы – процессы, у которых
первая производная
)(ty
выходной величины меняет знак. Эти
процессы имеют место ниже кривой GCF. В этой группе могут быть
выделены колебательные переходные процессы без перерегулирования,
когда
)()( yty
при всех t (область III), и колебательные переходные
процессы с перерегулированием, которые, в свою очередь,
подразделяются на переходные процессы с одним перерегулированием
1
0
(область IV), переходные процессы с двумя экстремумами (
%5
) и
1 2
(область V), переходные процессы с тремя и более
экстремумами и
,3,2,
1
i
i
(область VI), переходные процессы с
перерегулированием и двумя и более экстремумами и
,3,2,
1
i
i
(область VII).
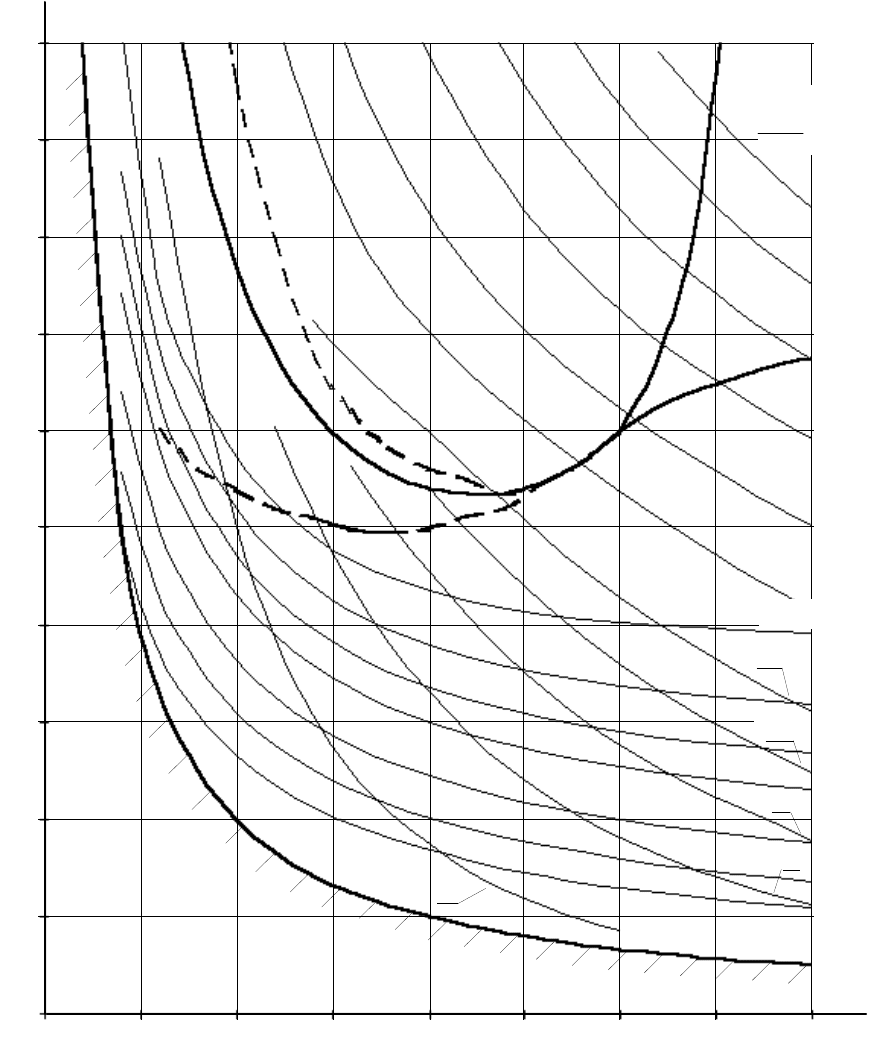
Следующим этапом построения диаграммы Вышнеградского
является нанесение линий равных значений показателей качества
работы контура. Расчет проведен методом моделирования. На рис. 2.38
приведены диаграммы качества регулирования с нанесенными линиями
равных значений перерегулирования
1
const
и относительного
времени первого согласования
T
t
)5(
1ру
= const.
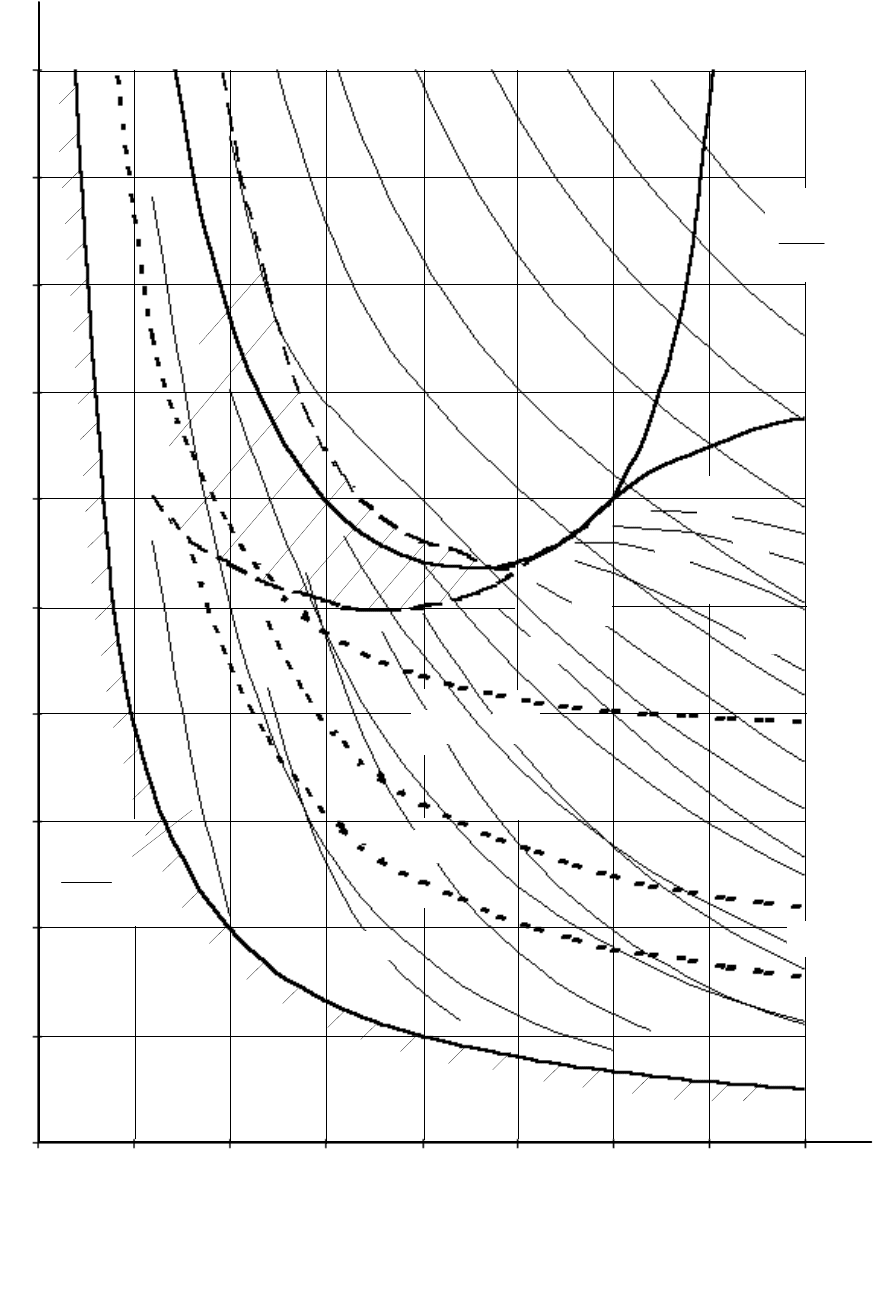
На диаграмме рис. 2.39 в дополнение к линиям
T
t
)5(
1ру
= const
нанесены линии равных значений относительного времени достижения
первого максимума
const
рум
T
t
. Цифрами 1, 2, 3 помечены области с
одним перерегулированием
%)( 5
1
, двумя
%)( 5
2
и тремя и более
экстремумами.
139
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
b
к
0.5 1 1.5 2 2.5 3 3.5 4
a
к
35
30
25
20
16
10 %
15 %
20 %
30 %
40 %
50 %
12
10
8
6
4
5 %
1
t
T
ру
( )
1
5
40
Рис. 2.38. Диаграммы качества системы третьего порядка
140
4.5
5
4
3.5
3
2.5
2
1.5
1
0.5
b
к
0.5 1 1.5 2 32.5 3.5 4
a
к
35
30
25
20
16
12
10
6
t
T
умр
4
6
4
8
10
12
16
20
25
30
35
40
1
2
3
3
8
2
1
%5
t
(
T
ру
)
1
5
40
%5
%5
Рис. 2.39. Диаграммы качества регулирования системы третьего порядка
Время переходного процесса
)5(
2ру
t
, т. е. окончательного вхождения
в зону
%5
от установившегося значения выходной координаты
контура, может быть определено следующим образом:
141
