Тверской Ю.С. Локальные системы управления

Подождите немного. Документ загружается.

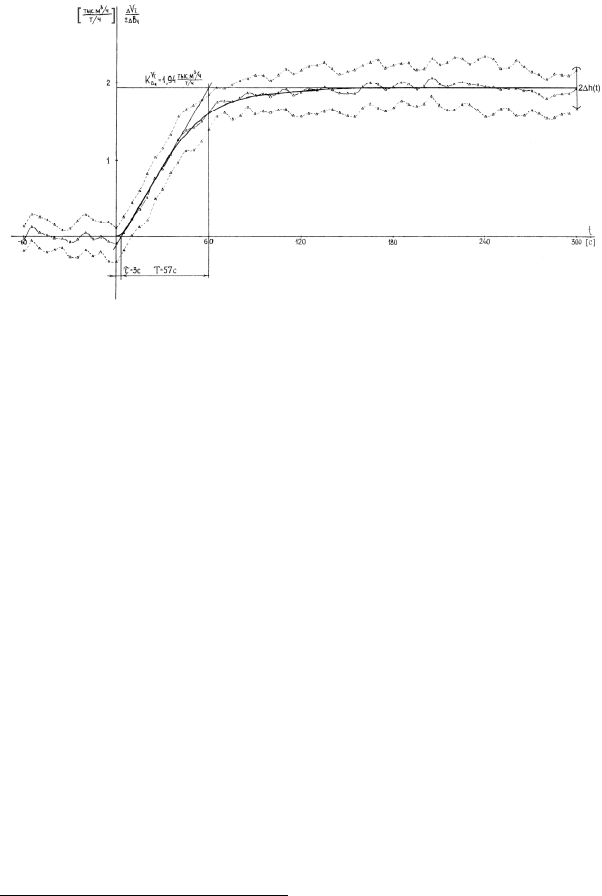
Рис. 4.1. Пример оценки переходной характеристики в зоне довери-

тельного интервала (изменение сигнала по расходу первичного воздуха

в мельницу возмущением подачей топлива)

Корректность проведенных экспериментов можно оценить пу-

тем наложения переходных характеристик, которые при малых

величинах возмущений должны практически совпадать. В про-

тивном случае имеет место проявление фактора нелинейности.

Рекомендуется применять также метод непосредственного

определения частотных характеристик каналов регулирования

путем подачи на вход объекта синусоидального сигнала задан-

ной частоты

и регистрации на выходе синусоидального сигнала

той же частоты, но сдвинутого по фазе и искаженного по ампли-

туде. Параметры КЧХ несложно определить по фигуре Лиссажу.

4.2. Фонд экспериментальных характеристик объектов

энергетики

4.2.1. «Фонд экспериментальных характеристик объектов

энергетики»

(далее «Фонд») представляет собой базу данных

экспериментальных динамических характеристик головного теп-

лоэнергетического оборудования (рис. 4.2, 4.3).

«Фонд» включен в состав интегрированной информационно-

технической среды многофункционального учебно-

исследовательского комплекса «Полигон АСУТП электростан-

ций».

См. лабораторный практикум по дисциплине [21].

Тверской Ю.С., Тверской Д.Ю., Харитонов И.Е. О создании фонда экспери-

ментальных динамических характеристик паровых котлов ТЭС // Новое в рос-

сийской электроэнергетике. – 2002. – № 12. – С.16–24.

Энергетическое

предприятие

7 ОГК, 14 ТГК

Объект

Электрические

станции

Тип объекта

Название станции

Тип станции

Установленная

мощность

Установка

Котел

Тип установки

Марка котла

Тип котла

Котел-утилизатор (да,

нет)

Режимная карта

Факты

Динамические характеристики

Параметры Y

«Выход модели

ТОУ»

Параметры X

«Вход модели

ТОУ»

Турбина

Тепломеханическое

оборудование (ТМО)

Топливоподготовительное

оборудование (ТПО)

Тип установки

Марка турбины

Тип турбины

Тип установки

Регулирующий орган

Тип регулирующего

органа

Тип установки

Тип мельницы

Тип сепаратора

Питатель сырого угля

(ПСУ)

Питатель пыли (ПП)

Статические характеристики

Статистические

характеристики

Комплексно-частотные

характеристики

Аналитические и

динамические модели

Тип установки

Вид рассматриваемой

модели

Условия

эксперимента

Режим, нагрузка и

др.

Параметры

характеристики

Шаг квантования

Количество точек

характеристики

Параметры экспресс-

аппроксимации и др.

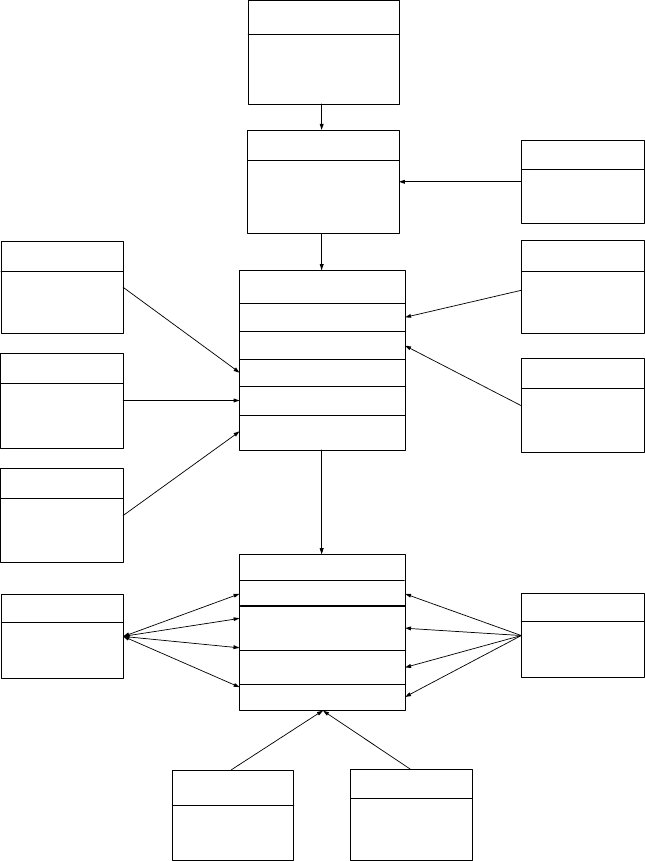
Рис. 4.2. Основные направления формирования «Фонда эксперимен-

тальных характеристик объектов энергетики»

Рис. 4.3. Стартовое окно «Фонда экспериментальных

характеристик объектов энергетики»

4.2.2. Применение «Фонда» совместно с ПМК «Темп» позво-

ляет выполнить оптимизацию АСР непараметрическими мето-

дами (рис. 4.4).

W(p) h(t)

W(jw)

W(m,jw)

Cопт

Экспериментальные

динамические

характеристики

КЧХ

Передаточные

функции

Станции

Котлы

Возмущения

Выходной парамет р

Режимная нагрузка

Параметры

Информация

Параметры

информации

Структура ПМК

«Темп» в виде

гиперграфа

Внутренняя

структура ПК

«Фонд»

ШАГ 1

ШАГ 4

ШАГ 2

Симою

М.П.

ЧАП

Рис. 4.4. К выбору маршрута проектирования

4.2.3. Пример.

Применение БД «Фонд» совместно с ПМК «ТЕМП».

ШАГ 1. Поиск экспериментальной переходной характеристики

канала ТОУ в «Фонде».

Исходные данные:

котёл – ТПЕ-208;

ТПО – ММТ-1500/2510-735;

сепаратор гравитационный;

возмущение – расход первичного воздуха;

выходной параметр – загрузка мельницы.

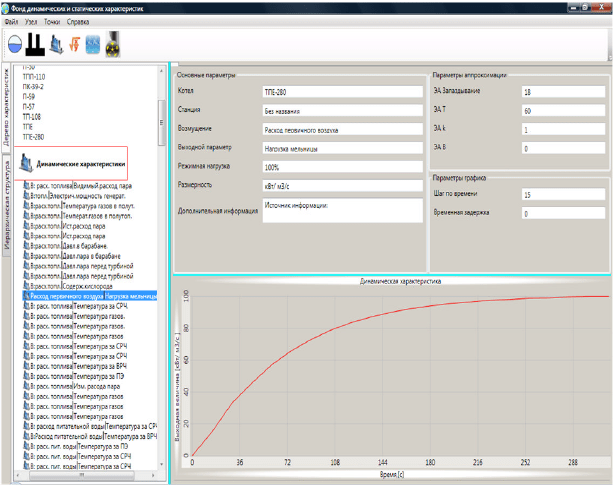
В «Фонде» в закладке «Иерархическая структура» в меню

выбираем строчку «Котлы/Станции/Характеристики», находим

соответствующий котел «ТПЕ-208» и соответствующую характе-

ристику по каналу «Расход первичного воздуха – Мощность дви-

гателя мельницы» (рис. 4.5).

Рис. 4.5. Экспериментальная динамическая характеристика в «Фонде»

ШАГ 2. Экспорт выбранной характеристики в ПМК «ТЕМП».

Для этого необходимо выполнить команду «Точки/записать

динамическую характеристику» в пользовательский файл ПМК

«ТЕМП» (файл f11.dat в системной папке ПМК «ТЕМП» [15] ).

Далее запускаем ПМК «ТЕМП». Для этого выполняем коман-

ду «Точки->Запустить ТЕМП» и контролируем загружаемую пе-

реходную характеристику (рис. 4.6).

Рис. 4.6. Переходная характеристика, загружаемая в ПМК «Темп»

ШАГ 3. Расчет комплексной частотной характеристики (КЧХ)

на основе загруженной переходной характеристики (рис. 4.7).

Рис. 4.7. Расчет КЧХ по переходной характеристике

Ключевыми факторами вычислительной процедуры опреде-

ления нормальной КЧХ путем непосредственного пересчета пе-

реходной характеристики являются время наблюдения переход-

ной характеристики Т (время усечения интеграла Лапласа) и шаг

квантования Δt. При этом условная частота среза КЧХ (послед-

няя достоверная точка вектора) может быть определена по

уточненной формуле Котельникова

= / Δt х k

Шаг по частоте Δω выбирается, как правило, равномерным

из расчета получения наибольшего количества расчетных точек

в третьем (ПИ-регулятор) и втором (ПИД-регулятор) квадрантах.

ШАГ 4. Пополнение «Фонда» расчетной (непараметрической)

КЧХ.

Для этого выполняем команду «Точки->Считать КЧХ» и осу-

ществляем просмотр КЧХ непосредственно в «Фонде». КЧХ мо-

жет храниться совместно с экспериментальной переходной ха-

рактеристикой (рис. 4.8).

ШАГ 5. Расчет области параметров настройки {С

;С

} по ис-

ходной переходной характеристике и оценке КЧХ (непарамет-

рический подход без использования аппроксимирующих пере-

даточных функций) средствами ПМК «Темп» для заданных

ограничений, например, на корневой m показатель колебатель-

ности методом расширенных характеристик [15] (рис. 4.9).

Для получения корректного результата необходимо обеспечить

сходимость интеграла Лапласа для заданного m, относительной

погрешности «усечения»  интеграла Лапласа и относительной

длительности времени наблюдения Т/Т

, где Т

– оценка постоян-

ной времени объекта при аппроксимации звеном первого порядка.

Оценка верхней границы диапазона расчетных частот может

быть получена также в виде ограничения [22, п.2.5] (табл.4.1):

, 0 1



  

  

Теорема Котельникова доказана для сигналов с ограниченным спектром

при условии равномерного квантования. Для функций с неограниченным спек-

тром теорему Котельникова можно рассматривать как приближенную. В этом

случае рекомендуют в формулу Котельникова вводить некоторый коэффициент

запаса k

з с





  ,

где коэффициент запаса k

рекомендуется выбирать в диапазоне 2  k

 3

(Ф.Е. Темников для информационной техники); 1,5  k

 6 (Ю.С. Тверской при

расчете КЧХ ОУ различной инерционности).

Таблица 4.1. Значения поправочного коэффициента 



=Т/Т



3 4 5 10

0,01 0 0 0,079 0,539

0,05 0,001 0,251 0,401 0,700

0,10 0,232 0,424 0,539 0,770

Рис. 4.8. Просмотр загруженной в «Фонд» КЧХ

СКО

м с

кВт

м с

кВт с



Рис. 4.9. Линия заданного запаса устойчивости в области параметров

настроек для одноконтурной АСР

5. Оценка адекватности математических

моделей

В этой части курсового проекта (работы) требуется

получить оценку меры адекватности математической модели ОУ.

5.1. Исследование динамических характеристик

имитационных моделей тренажеров

5.1.1. Исследование имитационной модели с получением пе-

реходных характеристик рассматривается на примере полигон-

ной версии АСУТП пылеугольного котла ТПЕ-208 с пылесисте-

мой прямого вдувания в составе «Полигона АСУТП электро-

станции».

Для получения переходной характеристики используется

ПМК «Тренд». Для этого нужно запустить полигонную версию

АСУТП пылеугольного котла ТПЕ-208 с пылесистемой прямого

вдувания (рис. 5.1).

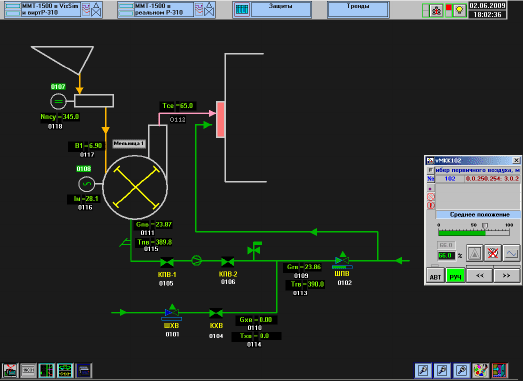
Рис. 5.1. Видеограмма (мнемосхема) АСУТП модели нитки

пылесистемы котла ТПЕ-208

5.1.2. Далее применяется методика экспериментального

определения динамических характеристик ТОУ (см. п. 4.1). С

этой целью на мнемосхеме с помощью регулирующего шибера

первичного горячего воздуха наносится возмущение величиной

до (±)10% ХРО.

После того как процессы изменения контролируемых пара-

метров установятся, определяется интервал времени Т, в тече-

ние которого проводился опыт.

5.1.3. Запускается станция анализа информации.

В рассматриваемом примере необходимо выделить сигналы

«Мощность двигателя мельницы» и «Расход первичного возду-

ха» (рис. 5.2).

Рис. 5.2. Станция анализа информации

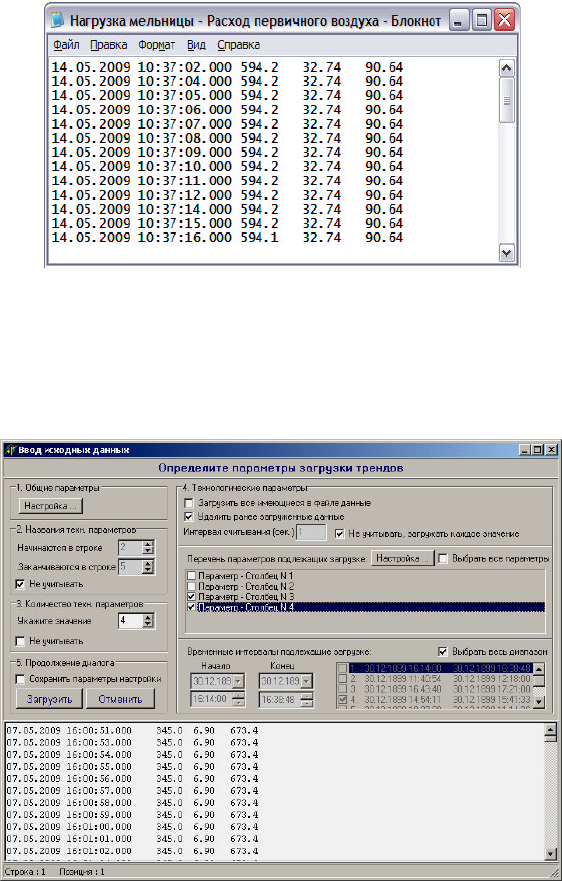
Далее тренды выделенных сигналов копируются в текстовый

файл (рис. 5.3).

Рис. 5.3. Тренды сигналов

5.1.4. Запускается ПМК «Тренд».

В верхнем левом углу окна выбирается функция «Считать

тренды». Указывается путь к текстовому файлу с необходимыми

трендами. В результате появляется окно загрузки трендов, в ко-

тором выполняется настройка ПМК «Тренд» (рис. 5.4).

Рис. 5.4. Окно загрузки трендов