Турищев Л.С. Численные методы решения задач строительства
Подождите немного. Документ загружается.

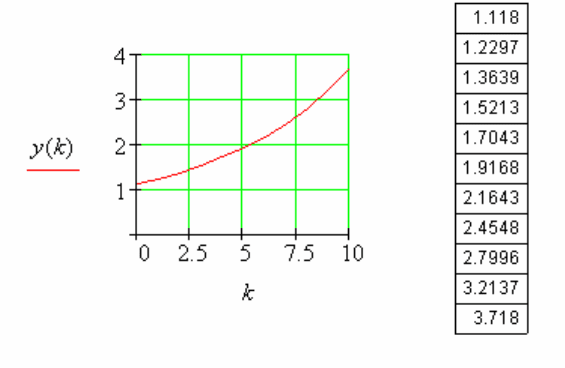
121
Следовательно, решение заданного уравнения имеет вид
)k(y y:)k(y n..:k
k
0
2. Подготовка к выполнению работы
2.1. Прочитайте теоретические основы работы.
2.2. Ознакомьтесь с выполненными примерами 5.1, 5.2, иллюстрирующи-
ми численную реализацию алгоритмов изучаемых методов в среде
MathCAD.
2.3. Получите у преподавателя свой вариант заданий для лабораторной
работы и приступите к ее выполнению, согласно изложенному ниже порядку.
3. Порядок выполнения работы
3.1. Запустите систему MathCAD и откройте окно для создания ново-
го документа.
3.2. Присвойте документу имя, включающее вашу фамилию и номер
лабораторной работы.
3.3. Сохраните документ в папке вашей группы.
3.4. Осуществите методом Рунге
-Кутта решение начальной задачи
для заданного дифференциального уравнения
.
3.5.
Осуществите методом конечных разностей решение краевой за-
дачи для заданного дифференциального уравнения
.
3.6. Введите необходимые текстовые комментарии к созданным ис-
полняемым блокам и полученным результатам.
3.7. Создайте заголовок лабораторной работы.
3.8. Предъявите преподавателю для просмотра выполненную и
оформленную лабораторную работу.
3.9. Закройте созданный документ и сохраните его в папке вашей
группы.
122
Лабораторная работа № 6
ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
Цель работы:
Научиться осуществлять численное решение основной задачи ли-
нейного программирования симплексным методом.
1. Теоретические основы работы
Существует три вида формулировок задачи линейного программиро-
вания:
общая задача;
стандартная задача;
основная задача.
В общей задаче линейного программирования требуется для линей-
ной целевой функции
n
j
jj
xccF
1
0
(6.1)
при заданных параметрах
n
c,...,c,c
10
найти n элементов решения
n
x,...,x
1
,
которые максимизируют или минимизируют функцию (6.1), удовлетворя-
ют системе
m ограничений общего вида (m < n)
)k ,...,i( bxa
i
n
j
jij
1
1
, (6.2)
)s ,...,ki( bxa
i
n
j
jij
1
1
, (6.3)
)m ,...,si( bxa
i
n
j
jij
1
1
, (6.4)
и требованию неотрицательности
)n ,...,j( x
j
10
. (6.5)
Так как отыскание наименьших значений линейной функции F экви-
валентно отысканию наибольших значений функции
F
F
, то решение
задач линейного программирования обычно связывают с отысканием од-
ного из экстремальных значений целевой функции.
123
В стандартной задаче линейного программирования для целевой
функции (6.1) требуется найти
n неотрицательных элементов решения
n
x,...,x
1
, которые ее максимизируют и удовлетворяют системе m ограни-
чений стандартного вида (
m < n)
)m ,...,i( bxa
i
n
j
jij
1
1
.
В основной задаче линейного программирования для целевой функ-
ции (6.1) требуется найти
n неотрицательных элементов решения
n
x,...,x
1
,
которые ее максимизируют и удовлетворяют системе m ограничений кано-
нического вида (
m < n)
)m ,...,i( bxa
i
n
j
jij
1
1
.
Методы решения задач линейного программирования основаны на
использовании канонической формы ограничений, поэтому при решении
задач линейного программирования осуществляется приведение ограниче-
ний, имеющих вид неравенств, к канонической форме.
Для приведения ограничений
-неравенств (6.2) и (6.3) к канонической
форме вводятся добавочные элементы решения
)s ,...,i( bxay
i
n
j
jiji
1
1
. (6.6)
Для выполнения добавочными элементами решения требования неотрица-
тельности ограничения вида (6.3) переменой знака в обеих частях приво-
дятся к виду (6.2).
Далее считается, что все элементы решения удовлетворяют ограни-
чениям в виде системы совместных линейных алгебраических уравнений
mnmnsmsm
nnss
bxa...xa...xa
...........................................
bxa...xa...xa
11
111111
. (6.7)
Общее решение системы (6.7) имеет вид
nmnmmmmm
nnmm
x...xx
.............................................
x...xx
11
111111
(6.8)
и выражает базисные переменные
m
x,...,x
1
через свободные
nm
x,...,x
1
.
Решение (6.8), для которого все свободные переменные равны нулю, назы-
вается базисным решением. Если в таком решении все базисные перемен-
124
ные неотрицательны )m ,...,j(
j
10
, то они допустимые, а само ре-
шение является опорным решением основной задачи линейного програм-
мирования. Оптимальное решение, в случае его существования, принадле-
жит конечному множеству опорных решений.
Целевая функция, выраженная через свободные переменные, описы-
вается соотношением
n
mj
jj
xccF
1
0
, (6.9)
где
m
i
ijijj
m
i
ii
cccccc
11
00
;
.
Основным методом решения основной задачи линейного програм-
мирования является симплексный метод. Алгоритм метода включает сле-
дующие процедуры:
нахождение начального опорного решения;
проверку оптимальности опорного решения;
переход к следующему опорному решению в случае неоптималь-
ности предыдущего опорного решения.
Численную реализацию метода удобно осуществлять с помощью
симплексной матрицы задачи. Для получения такой матрицы преобразуем
систему уравнений (6.7)
)m,...,k ,b(
)x(a...)x(a...)x(ab
...........................................
)x(a...)x(a...)x(ab
............................................
)x(a...)x(a...)x(ab
k
nmnsmsmm
nknskskk
nnss
10
0
0
0
11
11
111111
. (6.10)
Симплексная матрица формируется из параметров целевой функции (6.1),
свободных членов и коэффициентов системы (6.10) и имеет вид
mnmsmm
knkskk
ns
ns
aaaa
aaaa
aaaa
aaaa
~
10
10
111110
000100
a , (6.11)
где )n,...,i( ca ,ca
ii
1
0000
; )m,...,j( ba
jj
1
0
.

125
1.1. Алгоритм получения начального опорного решения
Для нахождения начального опорного решения выполняется m шагов
жордановых исключений. Они позволяют преобразовать систему уравне-
ний (6.7) к виду (6.8) и выделить некоторый набор допустимых базисных
переменных. На каждом шаге такой процедуры выделяется одна базисная
переменная, выражается через остальные элементы решения и исключает-
ся из других уравнений преобразуемой системы.
На первом шаге выделим переменную
s
x
в базисные переменные.
Будем считать коэффициент
ks
a
разрешающим, т. е. удовлетворяющим
требованиям
).mi ,a ;
a
b
min(
a
b
a
is
is
i
ks
k
ks
0
0
(6.12)
Тогда соответствующие коэффициенту
ks
a столбец и строка матрицы коэф-
фициентов системы (6.10) являются разрешающим столбцом и разрешающей
строкой первого шага процедуры выделения базисных переменных.
Выделение переменной
s
x в число базисных связано с выполнением
следующих преобразований элементов расширенной матрицы системы
(6.10). Элементы разрешающего столбца, за исключением разрешающего
коэффициента, умножаются на (
-1) и делятся на разрешающий коэффици-
ент. Все элементы разрешающей строки делятся на разрешающий коэффи-
циент. Преобразованные элементы разрешающего столбца и строки вы-
числяются по формулам
).n,...,j,sj(
a
a
a
)m,...,i,ki(
a
a
a
a
a
ks
kj
kj
ks
is
is
ks
ks
0
1
1
1
11
Остальные преобразованные элементы расширенной матрицы системы
(6.10) вычисляются по формуле
).n,...,j,sj;m,...,i,ki(
a
a
aaa
ks
is
kjijij
01
1
Целевая функция после выделения базисной переменной
s
x описывается
выражением

126
n
sj
j
jj
xccF
1
11
0
1
, (6.13)
где
).n,...,j,sj(
ca ,ca
a
a
ccc ,
a
b
ccc
jj
ks
kj
sjj
ks
s
s
1
11
0
1
0
1
00
1
0
1
0
В результате выполнения первого шага преобразований базисная пе-
ременная
s
x
исключается из правых частей системы уравнений (6.10), а
симплексная матрица задачи приводится к виду
111
1
1
0
111
1
1
0
1
1
1
1
1
11
1
10
1
0
1
0
1
01
1
00
1
mnmsmm
knkskk
ns
ns
aaaa
aaaa
aaaa
aaaa
~
a . (6.14)
Элементами матрицы (6.15) являются параметры целевой функции
(6.13) и преобразованные элементы расширенной матрицы системы (6.10),
исключая элементы разрешающего столбца.
Продолжая процесс выделения базисных переменных по описанной
схеме, после
m-ного шага будет сформирована следующая симплексная
матрица
m
mn
m
mm
m
m
m
n
m
m
m
m
n
m
m
m
m
aaa
aaa
aaa
~
10
11110
01000
a (6.15)
и получено начальное опорное решение
).m,...,i ,a(
ax,...,ax
m
i
m
mm
m
10
0
0101
(6.16)
Элементы матрицы (6.15) вычисляются по рекуррентным формулам

127
)n,...,mj ;m,...,i(
)ki(
a
a
aaa
)kj(
a
a
a ,
a
a
a
a
a
ccc ,ca
a
b
ccc ,ca
m
ks
m
is
m
kj
m
ij
m
ij
m
ks
m
kj
m
kj
m
ks
m
i
m
i
m
ks
m
kj
m
s
m
j
m
j
m
j
m
j
m
ks
m
s
m
s
mmmm
11
1
1
11
1
1
1
1
0
0
1
1
11
0
1
1
11
00000
.
С помощью элементов этой матрицы делается проверка оптимальности на-
чального опорного решения.
Если элементы нулевой строки этой матрицы, являющиеся парамет-
рами целевой функции, неотрицательны
)n,...,mj( a
m
j
10
0
, (6.17)
то полученное опорное решение является оптимальным. Соответствующее
ему максимальное значение целевой функции определяется величиной
элемента
max
m
Fa
00
.
Если один или несколько элементов нулевой строки матрицы (6.15)
не удовлетворяют условию (6.17), то полученное опорное решение не яв-
ляется оптимальным.
1.2. Алгоритм отыскания оптимального опорного решения
В случае неоптимальности начального опорного решения (6.16) для
нахождения нового опорного решения осуществляется следующий шаг
жорданова исключения для корректировки выделенных базисных пере-
менных. В их число включается свободная переменная при параметре це-
левой функции последнего шага выделения базисных переменных, не
удовлетворяющем критерию (6.17). В случае нескольких свободных пере-
менных с параметрами, не удовлетворяющими такому критерию, выбира-
ется переменная с наибольшим по модулю параметром. Разрешающий
элемент определяется из числа положительных коэффициентов разре-
шающего столбца в соответствии с требованиями (6.1
2).

128
При корректировке базисных переменных получение новых элементов
разрешающего столбца и разрешающей строки производится по формулам
).n,...,mj,sj(
a
a
a
a
b
b
)m,...,i,ki(
a
a
a
a
a
m
ks
m
kj
m
kj
m
ks
m
k
m
k
m
ks
m
is
m
is
m
ks
m
ks
1
1
1
11
11
Для получения остальных элементов используются формулы
).n,...,mj ;m,...,i ;ki(
a
a
aaa ,
a
b
b
m
ks
m
is
m
kj
m
ij
m
ij
m
ks
m
i
m
i
11
11
Процесс корректировки базисных переменных за счет свободных пе-
ременных и нахождение исправленных опорных решений продолжается до
тех пор, пока не будет найдено оптимальное решение или будет установ-
лено его отсутствие.
Оптимальное решение не существует, если для параметров целевой
функции, не удовлетворяющих (6.17), в соответствующих им столбцах
симплексной матрицы нет положительных величин для выбора разре-
шающего элемента. Это означает, что целевая функция (6.1) не ограниче-
на сверху.
Пример 6.1. Найти максимальное значение линейной целевой функции
21
35
x
x
F
при выполнении следующих ограничений на элементы решения:
)
,...,
j
(
x
x
x
x
x
x
x
x
x
x
x
x
x
j
510
72
72
4
5421
5321
4321
1. Исходные данные – симплексная матрица
a
5
4
7
7
3
1
1
2
1
1
2
1
0
1
1
0
0
1
0
1
0
0
1
1

129
2. Нахождение начального опорного решения
2.1. Первый шаг исключений – выделение элемента решения x
4
в
число базисных переменных.
Вычисление оценочных отношений элемента решения
x
4
a
1 0
a
1 4
4
a
3 0
a
3 4
7
Разрешающий элемент первого шага исключений
Разрешающий элемент первого шага исключений
1
41
,
а .
Преобразование элементов исходной симплексной матрицы:
– строка параметров целевой функции
j 0 4
a
1
0 j
a
0 j
a
0 4
a
1 j
a
1 4
j 3( ) a
0 5
a
0 4
a
1 5
a
1 4
j 4( )
– элементы разрешающей строки
a
1
1 j
a
1 j
a
1 4
j 3( )
a
1 5
a
1 4
j 4( )
– элементы остальных строк
i 2 3
a
1
i j
a
i j
a
1 j
a
i 4
a
1 4
j 3( ) a
i 5
a
1 5
a
i 4
a
1 4
j 4( )
Получение симплексной матрицы первого шага исключений
11033
11217
01114
00135
1
а
.
2.2.
Второй шаг исключений – выделение элемента решения x
5
в
число базисных переменных.
Вычисление оценочных отношений элемента решения
x
5
37
43
1
03
1
42
1
02
,
,
,
,
a
a
a
a
.
Разрешающий элемент второго шага исключений
a
,
1
43
.

130
Преобразование элементов симплексной матрицы первого шага ис-
ключений:
– строка параметров целевой функции
j 0 3
a
2
0 j
a
1
0 j
a
1
0 4
a
1
3 j
a
1
3 4
– элементы разрешающей строки
j 0 3
a
2
3 j
a
1
3 j
a
1
3 4
– элементы остальных строк
i 1 2
a
2
i j
a
1
i j
a
1
3 j
a
1
i 4
a
1
3 4
Получение симплексной матрицы второго шага исключений
1033
2244
1114
0135
2
а
.
2.3.
Третий шаг исключений – выделение элемента решения x
3
в чис-
ло базисных переменных.
Вычисление оценочных отношений элемента решения
x
3
24
32
2
02
2
31
2
01
2
,
,
,
,
a
a
a
a
.
Разрешающий элемент третьего шага
2
32
2
,
a .
Преобразование элементов симплексной матрицы второго шага ис-
ключений:
– строка параметров целевой функции
2
0
:
..
j
