Турчина Н.В. Физика в задачах для поступающих в вузы
Подождите немного. Документ загружается.

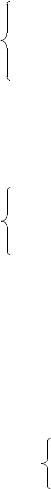
480
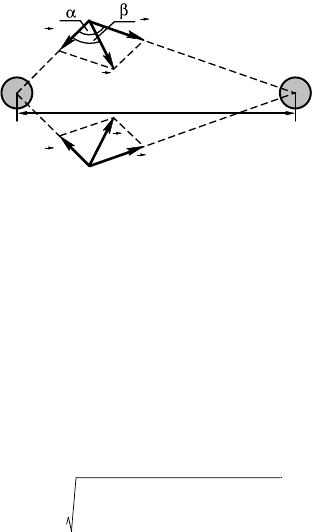
3.10.9. Пусть после удара шары 1 и 2 разлетаются под улами γ
и β оси ОX, причем γ + β = α.
Запишем заоны сохранения импульса (в проециях на оси OX
и OY) и энерии:
де m — масса аждоо шара, v — сорость первоо шара до удара,
v
1
и v
2
— сорости шаров после удара.
Разделим все уравнения на массу m, возведем в вадрат уравне-
ния (1), (2) и сложим их. В результате получим
Теперь вычтем из уравнения (4) уравнение (5):
0 = 2v
1
v
2
cos α.
Та а сорости после соударения не равны нулю, то, следова-
тельно, cos α = 0, т. е. α = 90°.
Ответ: α = 90°.
3.10.23. Запишем для первоо соударения убиов (рис. 3.10.20,
а, б) заоны сохранения импульса и энерии:
Решив данную систему уравнений, найдем сорости убиов m
и M после удара соответственно:
v
1
= v ,(3)
u = v .(4)
После первоо удара до второо уби m проходит путь s
1
= l + l
1
(рис. 3.10.21, в), уби M — путь s
2
= l
1
– l. Та а время движе-
ния убиов между ударами одинаовое (t
1
= t
2
), получим
= ⇒ = . (5)
mv = mv
1
cos β + mv
2
cos γ,(1)
0 = mv
1
sin β + mvsin γ, (2)
mv
2
= m + m ,(3)v
1
2
v
2
2
v
2
= + + 2v
1
v
2
cos α,(4)
v
2
= + . (5)
v
1
2
v
2
2
v
1
2
v
2
2
mv = Mu – mv
1
,
mv
2
= Mu
2
+ m
.
v
1
2
1()
2()
Mm−
Mm+
-----------------
2m
Mm+
-----------------
s
1
v
1
------
s
2
u
-----
ll
1
+()Mm−()
vM m−()
-----------------------------------------
l
1
l−()Mm+()
2mv
-----------------------------------------
481
Решив уравнение (5), находим l
1
= l = 9 м.
О т в е т: l
1
= 9 м.
3.10.29. Пусть u — оризонтальная составляющая сорости
шайбы и тела в момент отрыва шайбы. По заону сохранения им-
пульса
mv = (M + m)u.(1)
Кода шайба будет находиться в наивысшей точе подъема, ее
сорость станет равной u (а и у тела). По заону сохранения
энерии
= mgh +. (2)
Решив систему уравнений (1), (2), получим о т в е т:
h = .
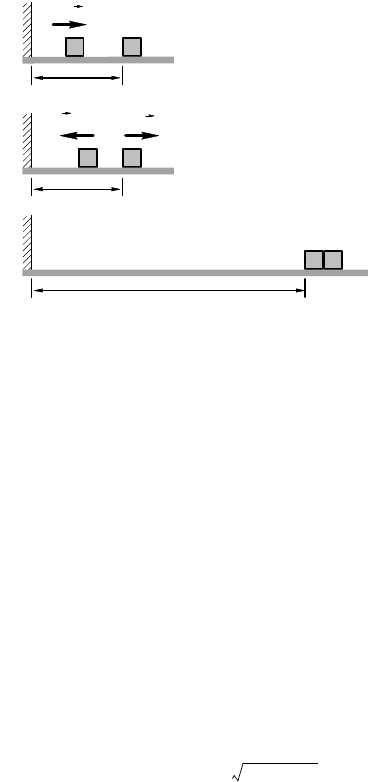
3.10.31. При движении шариа т из исходной точи C до дна
выеми (рис. 3.10.21, а) брусо М будет оставаться неподвиж-
ным. Сорость шариа в точе C найдем из заона сохранения
энерии:
mg(R + h) = , v
C
= . (1)
n 1+
n 3−
------------ -
v
mà)
á)
â)
M
l
u
m
m
M
M
l
l
1
v
1
Рис. 3.10.20
mv
2
2
-----------
Mm+()u
2
2
-----------------------------
Mv
2
2gm M+()
----------------------------- -
mv
C
2
2
----------- -
2gR h+()
482
При дальнейшем движении шариа в выеме в результате
взаимодействия с брусом шари будет толать брусо вправо.
В результате этоо брусо отодвинется от стени, и система «ша-
ри—брусо» станет замнутой в оризонтальном направлении.
В точе B вертиальная составляющая сорость шариа станет рав-
ной нулю, а оризонтальная — сорости бруса v (рис. 3.10.21, б).
Записав заон сохранения энерии системы и заон сохране-
ния импульса:
= + mgR, mv
C
= (M + m)v,
с учетом (1) получим
= + mgR, или Mh = mR.
Следовательно, h = = 4 см.
О т в е т: h = 4 cм.
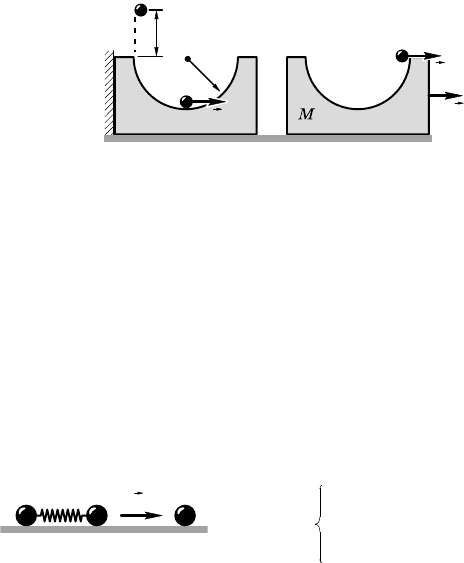
3.10.32. Запишем заоны сохранения импульса и энерии для
соударения шаров 1 и 3 (рис. 3.10.22):
де v
1
, v
3
— сорости рассматриваемых шаров после соударения.
Из решения системы уравнений следует, что
v
1
= 0, v
3
= v
0
,
т. е. первый шар после соударения остановится.
Теперь задачу можно переформулировать: на ладой поверх-
ности находятся два одинаовых шара, соединенных пружиной,
один из оторых (шар 2) имеет сорость v
0
, а второй (шар 1) поо-
ится.
m
A
M
à) á)
C
h
R
B
B
v
v
v
C
Рис. 3.10.21
mv
C
2
2
----------- -
Mm+()v
2
2
---------------------------- -
m 2gR h+()⋅
2
----------------------------------- -
m
2
2gR h+()⋅
2 Mm+()
-------------------------------------- -
mR
M
----------
1
2
3
k
v
0
Рис. 3.10.22
mv
0
= mv
1
+ mv
3
,
= + ,
mv
0
2
2
-----------
mv
1
2
2
-----------
mv
3
2
2
-----------

483
При дальнейшем движении шаров 1 и 2 в любой момент будут
выполняться заоны сохранения импульса и энерии системы
«шар 1 — пружина — шар 2». Несложно заметить, что при движе-
нии системы пружина будет то сжиматься, то растяиваться. Но
при масимальной и минимальной деформациях пружины со-
рости шаров будут одинаовы и равны сорости центра масс сис-
темы. Запишем заоны сохранения для одноо из таих моментов
времени:
mv
0
= 2mv, = 2 + ,
де v — сорость шаров в эти моменты. Отсюда получим:
∆x = äv
0
, l
max
= l
0
+ ∆x = l
0
+ v
0
d 13,6 см,
l
min
= l
0
– ∆x = 10 – v
0
d 6,5 см.
О т в е т: l
max
d 13,6 cм; l
min
d 6,5 cм.
Г л а в а 4. ГРАВИТАЦИЯ
4.1.11. Силу притяжения F, действующую со стороны шара
с полостью на маленьий шари, можно представить в виде разно-
сти двух сил притяжения: F
1
— силы, создаваемой целым шаром (без
полости), и F
2
— силы, оторую создавала бы полость, если бы она
была заполнена свинцом, т. е.
F = F
1
– F
2
,(1)
де, соласно заону всемирноо тяотения,
F
1
= G ,(2)
F
2
= G = G ,(3)
G — равитационная постоянная, M′ — масса свинца, оторый
может находиться в полости, если ее им заполнить:
M′ = ρ
св
æ = = . (4)
mv
0
2
2
-----------
mv
2
2
-----------
kx
2
∆
2
--------------
m
2k
------ -
m
2k
------ -
m
2k
------ -
mM
d
2
------------
mM′
d
R
2
--- -
−
⎝⎠
⎛⎞
2
----------------------
mM′
d
2
-------------
4
3
--- π
R
2
----
⎝⎠
⎛⎞
3
M
4
3
--- πR
3
---------------
4
3
--- π
R
2
----
⎝⎠
⎛⎞
3
⋅
M
8
----- -

484
Подставляя в (1) выражения (2), (3) с учетом (4), получим
ответ:
F = GM – = G .
4.1.13. Сила тяотения сплошноо
шара F
1
= , де M = πR
3
ρ —
масса сплошноо шара, ρ — плотность
свинца. Сила тяотения полости, за-
полненной свинцом, F
2
= G , де
M′ = πr
3
ρ, s — расстояние между центром полости и материальной
точой. (рис. 4.1.7). Сила взаимодействия шара с полостью и
материальной точой:
F = F
1
– F
2
⇒ F = .
Учтем, что s
2
= l
2
+ L
2
– 2lLcos α и l
2
= s
2
+L
2
– 2sLcos β, и,
решив данную систему уравнений, получим
F = πGmρ d 5,7 мН.
О т в е т: F d 5,7 мH.
4.1.14. Сила притяжения будет
равна еометричесой сумме сил при-
тяжения, создаваемых отдельными эле-
ментами сферы. Малые элементы σ
1
и σ
2
(рис. 4.1.8) вырезают из сферы онусы с
вершиной в точе A, оторые получают
при вращении образующей BC вору оси
S
1
S
2
. Площади элементов равны соот-
ветственно и , а их массы и , де
Ω — телесный уол, под оторым видны оба элемента из точи A, ρ —
поверхностная плотность сферы (масса, приходящаяся на единицу
площади), α
1
= α
2
, та а треуольни S
1
OS
2
равнобедренный.
Силы притяжения, создаваемые элементами, равны
F
1
= G = G , F
2
= G = G ,
де m — масса тела, и направлены в противоположные стороны.
Их равнодействующая равна нулю.
M
d
2
----- -
⎝
⎛
M
8
----- -
⎠
⎞
7mM
8d
2
---------------
A
l
C
s
L
F
F
1
F
2
B
Рис. 4.1.7
GMm
L
2
----------------
4
3
---
M′m
s
2
-------------
4
3
---
F
1
2
F
2
2
2F
1
F
2
βcos−+
4
3
---
R
6
L
4
------ -
r
6
L
2
l
2
−
------------------
2R
3
r
3
L 2l αcos−()
2L
2
L
2
l
2
−()l
2
L
2
2Ll αcos−+
---------------------------------------------------------------------------------------
−+
B
S
1
A
O
C
S
2
Рис. 4.1.8
AS
1
()
2
Ω
α
1
cos
------------------------
AS
2
()
2
Ω
α
2
cos
------------------------
AS
1
()
2
Ωρ
α
1
cos
----------------------------
AS
1
()
2
Ωρ
α
2
cos
----------------------------
mAS
1
()
2
Ωρ
AS
1
()
2
α
1
cos
------------------------------------
mΩρ
α
1
cos
--------------- -
mAS
2
()
2
Ωρ
AS
2
()
2
α
2
cos
------------------------------------
mΩρ
α
2
cos
--------------- -
485
Проводя аналоичные рассуждения для друих соответствую-
щих элементов сферы, убеждаемся, что все они попарно омпенси-
руют дру друа. Следовательно, сила притяжения, оторая дейст-
вует со стороны сферы на тело, помещенное внутри нее, равна ну-
лю, что и требовалось доазать.
4.2.3. Усорение свободноо падения у поверхности Земли
g
0
= G ,
де М
З
— масса Земли, R
З
— радиус Земли.
Аналоичное соотношение можно записать и для усорения сво-
бодноо падения у поверхности Луны:
g
Л
= G ,
де М
Л
, R
Л
— масса и радиус Луны.
Поделив одно уравнение на друое, получим
= .
По условию, R
З
= nR
Л
, M
З
= kM
Л
. Поэтому g
Л
= g
0
=
=1,65м/с
2
.
О т в е т: g
Л
= 1,65 м/с
2
.
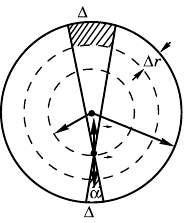
4.2.10. Поместим тело массой m внутри Земли в произволь-
ной точе А (рис. 4.2.1).
Мысленно разделим Землю на тоние
сферичесие слои толщиной ∆r (∆r n R
З
) и
рассмотрим один из них. Проведем онус с
малым улом раствора через точу А. Конус
вырежет из сферичесоо слоя массы ∆m
1
=
= ρS
1
∆r, ∆m
2
= ρS
2
∆r, оторые будут притя-
ивать точу m силами:
F
1
= G и F
2
= G ,
де r
1
,r
2
— расстояния от точи А
соответственно до массы ∆m
1
и массы ∆m
2
.
M
З
R
З
2
-------- -
M
Л
R
Л
2
---------- -
g
0
g
Л
-------
M
З
R
Л
2
R
З
2
M
Л
-----------------
n
2
k
------
F
1
F
2
R
Ç
r
2
A
m
1
m
2
Рис. 4.2.1
mm
1
∆
r
1
2
---------------- -
mm
2
∆
r
2
2
---------------- -
486
Учтя, что телесный уол α = = , получим, решив систему
приведенных уравнений:
= 1.
Из этоо следует, что результирующая сила, действующая на
массу m со стороны этоо слоя, равна нулю. Поэтому на точу m
действует тольо сила притяжения той массы Земли, оторая нахо-
дится внутри сферы радиусом r. Определим эту массу: M
1
=
= πr
3
ρ, де ρ — плотность Земли; отсюда находим ρ = .
Поэтому
F = G = G = mg
0
.
О т в е т: F = mg
0
.
4.2.13. Усорение свободноо падения на Солнце
g
С
= G ,(1)
де M
C
и R
C
— масса и радиус Солнца.
Радиус Солнца R
C
найдем из еометричесоо соотношения
R
C
= = , (2)
де R — расстояние от Земли до Солнца, α — уол, под оторым ви-
ден диаметр Солнца с Земли.
Массу Солнца определим, применив второй заон Ньютона дви-
жению Земли вору Солнца:
F = M
З
a, G = M
З
,
M
С
= . (3)
Из выражений (1)—(3) получим о т в е т:
g
С
= = 274 м/с
2
.
S
1
r
1
2
------
S
2
r
2
2
------
F
1
F
2
------
4
3
---
3M
З
4πR
З
3
--------------
mM
1
r
2
--------------
mM
З
r
3
R
З
3
r
3
---------------------
r
R
З
------ -
r
R
З
------ -
M
C
R
C
2
-------- -
D
2
----
R αsin
2
-----------------
M
З
M
С
R
2
------------------ -
4π
2
R
T
З
2
--------------
4π
2
R
3
GT
З
2
-----------------
16π
2
R
T
З
2
sin
2
α
-----------------------
487
4.2.22. Из рис. 4.2.2 видно, что таие точи лежат на оруж-
ности в плосости, перпендиулярной прямой, соединяющей эти
звезды. Решим задачу для произвольной точи А этой оружности.
По принципу суперпозиции g = g
1
+ g
2
, де g
1
и g
2
— усорения
свободноо падения, обусловленные притяжением первой и второй
звезд соответственно:
g
1
= G ; g
2
= G .
Из веторных треуольниов находим:
g
2
= + – 2g
1
g
2
cos α;
l
2
= + – 2r
1
r
2
cos α.
Решив систему приведенных уравнений, получим о т в е т:
g = G ;
вычислив модуль g, найдем и направление g, определяемое, напри-
мер, улом β:
β = arc cos .
4.4.2. На спутни массой m
с
действует сила равитации
F = , оторая сообщает ему центростремительное усорение
a = :
G = m
с
.
g
2
m
2
r
2
g
1
m
1
r
1
r
1
’
r
2
’
g
1
’
A’
g
2
’
g’
l
A
g
Рис. 4.2.2
m
1
r
1
2
--------
m
2
r
2
2
--------
g
1
2
g
2
2
r
1
2
r
2
2
m
1
2
r
1
4
--------
m
2
2
r
2
4
--------
m
1
m
2
r
1
3
r
2
3
---------------- l
2
r
1
2
− r
2
2
−()−+
g
2
2
− g
1
2
g
2
++
2gg
1
-----------------------------------
Gm
с
M
З
R
З
h+()
2
------------------------
v
2
R
З
h+
-----------------
m
с
M
З
R
З
h+()
2
------------------------
v
2
R
З
h+
-----------------
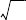
488
Для тела массой m на поверхности Земли можно записать:
mg
0
= .
Период и частота вращения спутниа соответственно равны:
T = , ω = .
Решив систему приведенных уравнений, получим о т в е т :
T = .
4.4.7. На Землю со стороны Солнца действует сила равитации,
оторая и сообщает ей центростремительное усорение a
n
= m
З
ω
2
R
З.С
.
Запишем второй заон Ньютона:
= m
З
a
n
.
Следовательно, масса Солнца
M
С
= = 2,2 · 10
30
= 2,2 · 10
27
т.
4.4.12. Во время движения осмичесоо орабля ео центро-
стремительное усорение
a
п
= R,(1)
де R — расстояние от орабля до центра Земли.
На осмонавта действуют силы: F
1
— сила притяжения осмо-
навта Землей F
1
= G , F
2
— сила притяжения осмонавта Лу-
ной F
2
= G , де R
З
— радиус Земли , N — сила, с
оторой орабль действует на осмонавта.
Если за положительное направление выбрать направление от
Луны Земле, то с учетом выражения (1) можно записать второй
заон Ньютона:
G – G + N = Rm.
GmM
З
R
З
2
-------------------
2π
ω
------ -
v
R
З
h+
-----------------
2π R
З
h+()
3
2
---
R
З
g
0
--------------------------------
Gm
З
M
C
R
З.С
2
----------------------
ω
2
R
З.С
2
G
-------------------
4π
2
T
2
--------- -
⎝
⎛
mM
З
R
2
---------------
⎠
⎞
⎝
⎛
mM
Л
60R
З
R−()
2
---------------------------------
⎠
⎞
mM
З
R
2
---------------
mM
Л
60R
З
R−()
2
---------------------------------
4π
2
T
2
--------- -
489
Из условия, что силы притяжения осмонавта Землей и Луной
равны дру друу, получим:
G = G ; R
2
= (60R
З
– R)
2
;
2R
2
– 243R
З
R + 7290 = 0;
R
1,2
= = R
З
;
R
1
= 67,5R
З
; R
2
= 54R
З
.
Первый орень R
1
= 67,5R
З
не удовлетворяет условию, та а
данное расстояние должно быть меньше 60R
З
, т. е. осмичесий о-
рабль находится на расстоянии R = 54R
З
от центра Земли,
следовательно,
N = Rm = 0,17 H.
Эта сила сообщает телу центростремительное усорение и на-
правлена Земле. Тода вес осмонавта, т. е. сила, с оторой он
давит на стену орабля, равен 0,17 H и направлен по прямой,
соединяющей центры Земли и Луны, в сторону Луны. Для этоо
реативные двиатели орабля должны работать, выбрасывая
азы в направлении от Земли Луне.
О т в е т: N = 0,17 H.
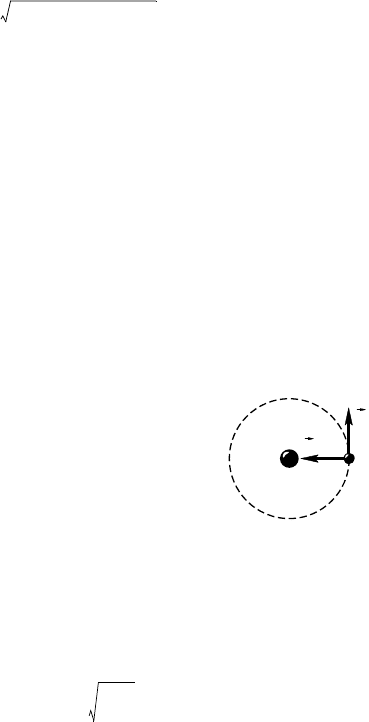
4.4.14. Масса Солнца М
С
мноо больше
массы Земли М
З
, поэтому можно считать, что
Солнце неподвижно, а Земля движется вору
Солнца по оружности радиусом r, равным
расстоянию между Землей и Солнцем (рис. 4.4.1).
На Землю действует сила равитационноо
притяжения F = = G , оторая создает ей
центростремительное усорение a
ц. с
= r, де Т — период обра-
щения Земли. По второму заону Ньютона F = ma
ц. с
. Из приведен-
ных соотношений выразим период обращения Земли (земной од):
T = 2πr .(1)
mM
З
R
2
---------------
mM
Л
60R
З
R−()
2
---------------------------------
M
З
M
Л
----------
243R
З
59049R
З
2
58320R
З
2
−±
4
-------------------------------------------------------------------------------------
243 27±()
4
----------------------------
4π
2
T
2
--------- -
F
C
v
З
Рис. 4.4.1
М
С
М
З
r
2
------------------ -
4π
2
T
2
--------- -
r
GM
С
------------- -
