Турчина Н.В. Физика в задачах для поступающих в вузы
Подождите немного. Документ загружается.

470
де v — сорость сано в точе 2, m — масса человеа. Та а вес
человеа равен силе реации N
1
сано, то
N
1
= 2mg.
Сорость v на участе 1–2 найдем из заона сохранения энерии:
Mg(H – h) = Mv
2
^ v = .
Следовательно,
= 2mg – mg ,
де учтено, что cos α = .
С учетом выражения (1) для H находим
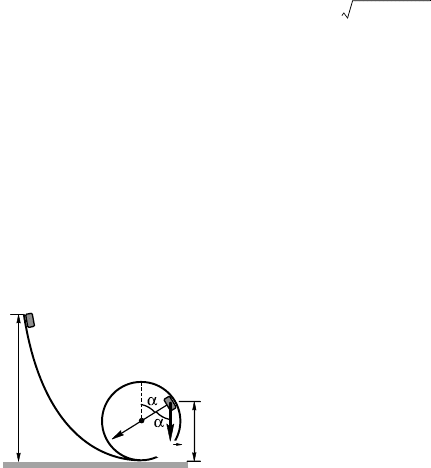
h = (2μl – R) = 0,67 м.
О т в е т: h = 0,67 м.
3.8.15. При переходе шайбы из состояния 1 в состояние 2
(рис. 3.8.13) выполняется заон сохранения энерии:
mgH + A = mgh + . (1)
В момент отрыва шайбы N = 0, по-
этому второй заон Ньютона для шайбы
в состоянии 2 имеет вид
mgcos α = , (2)
де (рис. 3.8.13)
cos α = . (3)
Решив систему уравнений (1)—(3), получим
A = (3h – R – 2h) = –0,44 Дж.
О т в е т: A = –0,44 Дж.
3.8.18. По заону сохранения энерии
– μ
1
m
1
gx = , (1)
де x — сжатие (удлинение) пружины моменту отрыва второо
бруса.
1
2
---
2gH h−()
m 2gH h−()⋅
R
-------------------------------------
Rh−
R
--------------
Rh−
R
--------------
1
3
---
1
2
h
mg
X
H
Рис. 3.8.13
mv
2
2
-----------
mv
2
R
-----------
hR−
R
--------------
mg
2
--------
m
1
v
2
2
--------------
kx
2
2
--------- -
471
Чтобы второй брусо сдвинулся, необходимо выполнение условия
F
упр
= F
тр
, т. е. kx = μ
2
m
2
g. (2)
Решив систему уравнений (1), (2), получим
v = g d 5,03 м/с.
О т в е т: v d 5,03 м/с.
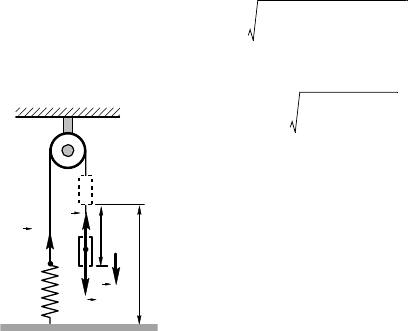
3.8.19. Запишем заон сохранения энерии при переходе сис-
темы из состояния 1 в 2 (рис. 3.8.14):
mgx + Fx + = . (1)
По условию равновесия руза М в состоянии 1:
mg = kx
0
.(2)
Решив систему уравнений (1), (2), получим о т в е т:
F
min
= = 4 H.
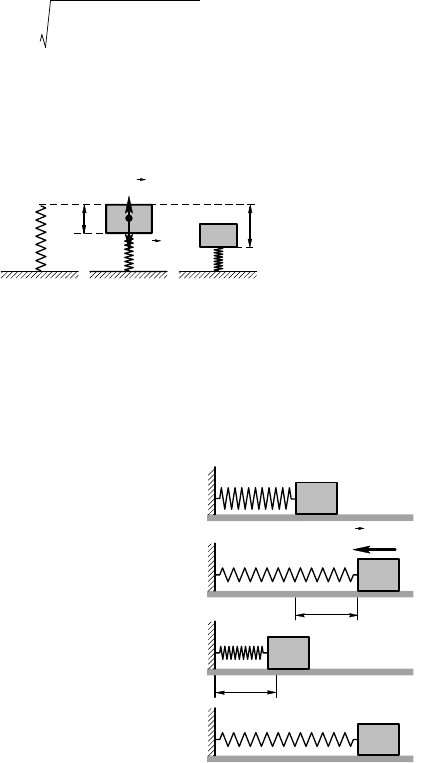
3.8.23. Если брусу сообщить
сорость, то он из начальноо поло-
жения 1 (рис. 3.8.15) будет двиаться,
сжимая пружину, до точи, в оторой
ео сорость будет равна нулю (состоя-
ние 2). Затем пружина будет толать
брусо в противоположном направле-
нии, и, по условию задачи, он должен
вернуться в начальное положение
(состояние 3). Та а начальная со-
рость минимальна, то сорость руза в
состоянии 3 должна быть равна нулю.
При движении бруса из состояния 1
в состояние 3 ео начальная инети-
чесая энерия должна быть равна ра-
боте сил трения:
E
1
+ A
тр1
= 0,
μ
2
m
2
k
-------------- 2μ
1
μ
2
m
2
m
1
------- -+
⎝⎠
⎛⎞
kx
0
2
2
----------
kx
0
x+()
2
2
---------------------------
Рис. 3.8.14
F
упр
x
0
x
0
+ x
1
2
mg
kx
2
------ -
v
0
l
1
m
1
l
2
m
m
3
m
k
Рис. 3.8.15
472
де E
1
= — инетичесая энерия бруса в состоянии 1,
A
тр1
= –2μmg(l + l
1
) — работа силы трения при движении бруса
из состояния 1 в состояние 3, l
1
— масимальное сжатие пружи-
ны в состоянии 2. Из приведенных уравнений получим
= 2μmg(l + l
1
). (1)
При переходе системы из состояния 2 в состояние 3 соласно за-
ону сохранения энерии имеем
E
n2
+ A
тр2
= E
п3
,
де E
п2
= — потенциальная энерия пружины в состоянии 2,
А
тр2
= – μmg(l + l
1
) — работа силы трения при движении бруса из
состояния 2 в состояние 3, Е
п3
= — потенциальная энерия
пружины в состоянии 3. Следовательно,
– μmg(l + l
1
) = .
Из данноо соотношения найдем
l
1
= + .
Решив систему уравнений (1), (2), получим
v
0
= d 1,4 м/с.
О т в е т: v
0
d 1,4 м/с.
3.8.24. Сорость тела будет масимальной
в момент прохождения им положения равнове-
сия (рис. 3.8.16). В этом положении справедли-
во равенство
mg = F
упр
, или mg = kx,(1)
де x — растяжение пружины в этот момент.
Из (1) находим x = d 9,8 см < h. Выбрав
нулевой уровень отсчета потенциальной энер-
mv
0
2
2
-----------
mv
0
2
2
-----------
kl
1
2
2
--------
kl
2
2
--------
kl
2
1
2
---------- -
kl
2
2
--------
μmg
k
------------
μmg
k
------------
⎝⎠
⎛⎞
2
2
μmg
k
------------ ll
2
++
F
тр
v
max
h
x
m
k
mg
T
Рис. 3.8.16
8μgl
μmg
k
------------
+
⎝⎠
⎛⎞
mg
k
--------

473
ии на уровне пола с учетом, что x < h, заон сохранения механиче-
сой энерии для системы представим в виде
mgh = mg(h – x) + + , (2)
де v
max
— масимальная сорость тела.
Из соотношений (1), (2) получим
v
max
= g = 1 м/с.
К моменту удара тела о пол пружина будет растянута на величину h,
и заон сохранения механичесой энерии системы примет вид
mgh = + ,
де v — сорость тела моменту ео удара о пол. При абсолютно не-
упруом ударе инетичесая энерия тела перейдет во внутреннюю.
Следовательно,
Q = , Q = mgh – = 34,5 мДж.
О т в е т: v
max
= 1 м/с; Q = 34,5 мДж.
3.8.25. Запишем второй заон Ньютона для аждоо тела сис-
темы (рис. 3.8.17):
m
1
a
1
= μm
1
g,
ma
2
= μm
1
g – T,
m
2
a
2
= T – m
2
g.
kx
2
2
--------- -
mv
max
2
2
------------------ -
m
k
---- -
kh
2
2
--------- -
mv
2
2
-----------
mv
2
2
-----------
kh
2
2
--------- -
F
тр
a
2
v
0
a
1
F
тр
T
a
2
m
2
g
m
1
g
Mg
T
Рис. 3.8.17

474
Заоны движения бруса, доси, руза соответственно имеют
вид:
v = v
0
– a
1
t, v = a
2
t, h = .
По условию v = v . Решив систему приведенных уравнений, полу-
чим
h = = 0,33 м.
К моменту, ода брусо перестанет сользить по досе, выде-
лится оличество теплоты
Q = – – m
2
gh.
Следовательно,
Q = m
1
– d 21,2 Дж.
О т в е т: h = 0,33 м; Q d 21, 2 Дж.
3.9.2. Запишем заоны сохранения импульса и сохранения
энерии:
m
1
v
1
– m
2
v
2
= 0, (1)
+ = E. (2)
Решим систему уравнений (1), (2), учтя, что M = m
1
+ m
2
(по условию), и получим
E = = 12 Дж.
О т в е т: E = 12 Дж.
3.9.5. Та а внешние силы на частицы не действуют, то сис-
тему из двух данных частиц считаем замнутой, и, следовательно,
импульс системы сохраняется:
p
до
= p
после
или m
1
v
1
+ m
2
v
2
= m
2
v.
Учтя, что m
1
= m
2
и v
1
B v
2
(по условию), получим
v = = 10 = 22,36 м/с.
б
д,
a
2
t
2
2
------------
б
д,
μm
1
m
2
−()m
2
M+()v
0
2
2g μ m
1
m
2
M++()m
2
−[]
----------------------------------------------------------------------
mv
0
2
2
-----------
m
1
m
2
M++()v
2
2
----------------------------------------------
v
0
2
2
----- -
m
1
μm
1
m
2
−()
μ m
1
m
2
M++()m
2
−
----------------------------------------------------------
m
1
v
1
2
2
---------------- -
m
2
v
2
2
2
---------------- -
Mv
1
v
2
2
------------------ -
v
1
2
v
2
2
+ 5
475
Из заона сохранения энерии найдем оличество теплоты, вы-
делившееся в системе:
Q = + – = + – = 0.
О т в е т: v = 22,36 м/с; Q = 0.
3.9.6. Запишем заоны сохранения импульса и энерии:
(m
1
v
1
)
2
+ (m
2
v
2
)
2
= (m
1
+ m
2
)
2
u
2
,(1)
+ = + Q. (2)
Решив систему уравнений (1), (2), получим о т в е т:
Q = = 0,84 Дж.
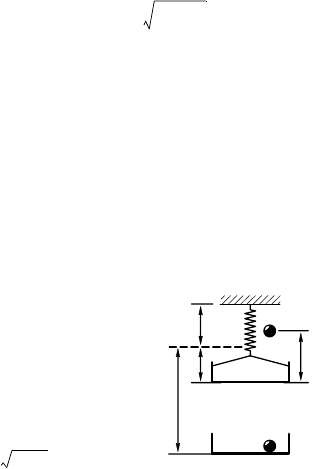
3.9.13. Пусть длина недеформированной
пружины равна l
0
(рис. 3.9.15), а удлинение
пружины, соответствующее положению рав-
новесия чаши без руза, x
0
.
Вначале руз падает и в момент асания
верхнео бруса будет иметь сорость u, ото-
рую найдем из заона сохранения энерии:
mgh = mu
2
^ u = .
Посольу соударение руза с чашой весов абсолютно неупру-
ое, то можно записать заон сохранения импульса:
mu = (M + m)v
0
,
де v
0
— сорость руза и чаши сразу после взаимодействия.
За счет приобретенной инетичесой энерии чаша с рузом пе-
рейдет в положение 2, в отором удлинение пружины станет рав-
ным x. Принимая за нулевой уровень отсчета потенциальной энер-
ии тел нижний онец недеформированной пружины, заон сохра-
нения энерии при переходе системы из положения 1 в положение 2
запишем в виде
– (M + m)gx
0
+ = – (M + m)gx + ,
де v — сорость чаши с рузом в положении 2.
m
1
v
1
2
2
--------------
m
2
v
2
2
2
--------------
m
2
v
2
2
--------------
m
2
---- -
⎝
⎛
v
1
2
v
2
2
⎝
⎛
v
1
2
v
2
2
+
⎠
⎞
2
⎠
⎞
m
1
v
1
2
2
--------------
m
2
v
2
2
2
--------------
m
1
m
2
+()u
2
2
--------------------------------- -
m
1
m
2
v
1
2
v
2
2
+()
2 m
1
m
2
+()
----------------------------------------
M
x
k
m
H
1
2
l
0
x
0
Рис. 3.9.15
1
2
---
2gH
Mm+()v
0
2
2
---------------------------- -
kx
0
2
2
--------- -
Mm+()v
2
2
---------------------------- -
kx
2
2
--------- -

476
Дополнив систему приведенных уравнений условием равнове-
сия чаши в положении 1:
Mg = kx
0
,
получим
– (M + m) + = – (M + m)gx + ,
или
v = .
После преобразований найдем зависимость сорости системы от
деформации пружины:
v = (–400x
2
+ 19,6х – 0,3)
1/2
.
3.9.19. Если убрать упор, например, у руза массой M, то в мо-
мент, ода пружина полностью распрямится, он будет иметь со-
рость v
1
, оторую найдем из заона сохранения энерии системы:
k = M , v
1
= x
0
,
де x
0
— начальная деформация пружины.
После этоо оставшийся упор уже не будет давить на руз мас-
сой m, и система в оризонтальном направлении будет замнутой.
При этом сорость центра масс системы остается постоянной и рав-
ной начальной (в момент отрыва руза массой m от упора). Из зао-
на сохранения импульса
Mv
1
= (M + m)v
ц. м
найдем сорость центра масс:
v
ц. м
= , или v
ц. м
= .
При дальнейшем движении пружина будет замедлять движе-
ние руза массой M и усорять руз массой m. Но посольу у руза
массой M моменту отрыва второо руза от упора будет неоторая
сорость, то пружина сначала продолжит растяиваться, и ее де-
формация будет наибольшей, ода сорости рузов станут равны-
ми. В этот момент системa будет двиаться а одно целое со соро-
стью центра масс. Из заона сохранения энерии:
= k + (M + m) ,
m
2
gH
Mm+
-----------------
Mg
2
k
------------
M
2
g
2
2k
---------------
Mm+()v
2
2
---------------------------- -
kx
2
2
--------- -
k
Mm+
----------------- x
2
2gx
Mg
2
2Mm+()
kM m+()
----------------------------------------
−
2m
2
gH
Mm+()
2
------------------------ -
++
1
2
---
x
0
2
1
2
---
v
1
2
k
M
----- -
Mv
1
Mm+
-----------------
Mx
0
Mm+
-----------------
k
M
------
1
2
---
kx
0
2
1
2
---
x
1
2
1
2
---
v
ц.м
2
477
де x
1
— масимальное удлинение пружины, получим
x
1
= x
0
.(1)
Если убрать упор у руза массой m, то, очевидно, масимальное
удлинение пружины
x
2
= x
0
.(2)
Из (1) и (2) находим
= = 2.
О т в е т: в 2 раза изменится масимальное растяжение пружины.
3.10.2. Запишем заон сохранения импульса:
m
1
v
1
+ m
2
v
2
= m
1
u
1
+ m
2
u
2
(1)
и заон сохранения энерии:
+ = + . (2)
Решив систему уравнений (1), (2), получим
u
1
= . (3)
По условию задачи u
1
= 0, поэтому из уравнения (3) находим
2m
2
v
2
+ m
1
v
1
– m
2
v
1
= 0,
отуда
= 1 – 2 = .
О т в е т: m
1
/m
2
= 1/3.
3.10.3. При соударении тел выполняются заон сохранения
импульса и заон сохранения энерии:
p
0
= p
1
+ p
2
,
E
1
= + .
Импульс и энерия тела связаны соотношениями:
E
1
= , = , = .
m
Mm+
-----------------
M
Mm+
-----------------
x
2
x
1
----- -
M
m
----- -
m
1
v
1
2
2
--------------
m
2
v
2
2
2
--------------
m
1
u
1
2
2
--------------
m
2
u
2
2
2
--------------
2m
2
v
2
v
1
m
1
m
2
−()+
m
1
m
2
+
----------------------------------------------------------
m
1
m
2
--------
v
2
v
1
------
1
3
---
E
2
′
E
1
′
p
0
2
2m
---------
E
2
′
p
2
2
2m
2
------------
E
1
′
p
1
2
2m
1
------------
478
Решив систему приведенных уравнений, получим
= = 0,62 Дж,
E
1
= + = 5,62 Дж.
О т в е т: инетичесая энерия первоо тела до удара E
1
=
= 5,62 Дж, после удара = 0,62 Дж.
3.10.7. Заон сохранения импульса при любом соударении
имеет вид
Mv
0
= Мu + mv,
отуда
u = v
0
– . (1)
По заону сохранения инетичесой энерии при любом упруом
соударении
= + . (2)
Решив систему уравнений (1), (2), найдем сорость
v = .
После первоо удара сорость второо шариа (M = m/2) равна
v
2
= = v;
после второо удара третий шари (M = m/4) движется со соростью
v
3
= = v
2
= v,
а после третьео удара сорость четвертоо шариа (M = m/8)
v
4
= = v
3
= v.
После аналоичных рассуждений находим, что сорость восьмоо
шариа после седьмоо удара равна
v
8
= v d 9,989 м/с.
Ответ: v
8
d 9,989 м/с.
E
1
′
E
2
′
m
1
m
2
−()
2
4m
1
m
2
-------------------------------------
E
2
′
E
1
′
E
1
′
mv
M
--------
Mv
0
2
2
------------
Mu
2
2
------------ -
mv
2
2
-----------
2Mv
0
mM+
-----------------
4mv
0
2mm+
--------------------
4
3
---
4mv
2
2mm+
--------------------
4
3
---
4
3
---
⎝⎠
⎛⎞
2
4mv
3
2mm+
--------------------
4
3
---
4
3
---
⎝⎠
⎛⎞
3
4
3
---
⎝⎠
⎛⎞
7
479
3.10.8. Рассмотрим абсолютно упруое
центральное соударение двух тел массами
m
1
и m
2
, движущихся со соростями v
1
и v
2
(рис. 3.10.18). Запишем заоны сохране-
ния импульса и энерии соответственно:
m
1
v
1
+ m
2
v
2
= m
1
u
1
+ m
2
u
1
,(1)
+ = + , (2)
де v
1
, v
2
— сорости тел после соударения.
Перепишем уравнения (1) и (2) в виде
m
1
(v
1
– u
1
) = m
2
(u
2
– v
2
), (3)
m
1
(v
1
– u
1
)(v
1
+ u
1
) = m
2
(u
1
– v
2
)(u
2
+ v
2
). (4)
Сорости тел после cоударения будут направлены вдоль той же
прямой, что и до нео. Поэтому из (3), (4) имеем
v
1
+ u
1
= v
2
+ u
2
.(5)
Решая систему уравнений (1)—(5), находим сорости тел после
соударения:
u
1
= , u
2
= . (6)
Воспользуемся формулами (6) для решения задачи.
Посольу сорость шариа массой m
2
больше сорости шари-
а массой m
1
, то после первоо соударения сорости шариов будут
равны:
u
1
= = 13,75 м/с,
u
2
= = 8,75 м/с
и направлены в одну сторону (рис. 3.10.19).
При следующем соударении (см. рис. 3.10.18) сорости шариов
= = 10 м/с,
= = 15 м/с.
Ка видим, после второо соударения сорости шариов стали та-
ими же, а до первоо. Лео понять, что при нечетных номерах
столновений сорости шариов будут u
1
, u
2
, а при четных , .
О т в е т: = 10 м/с; = 15 м/с.
m
1
u
1
m
2 u
2
m
1
m
2
v
2
v
1
Рис. 3.10.18
Рис. 3.10.19
m
1
v
1
2
2
--------------
m
2
v
2
2
2
--------------
m
1
u
1
2
2
--------------
m
2
u
2
2
2
--------------
m
1
m
2
−()v
1
2m
2
v
2
+
m
1
m
2
+
----------------------------------------------------------
m
2
m
1
−()v
2
2m
1
v
1
+
m
1
m
2
+
----------------------------------------------------------
m
1
m
2
−()v
1
2m
2
v
2
+
m
1
m
2
+
----------------------------------------------------------
m
2
m
1
−()v
2
2m
1
v
1
+
m
1
m
2
+
----------------------------------------------------------
u
1
′
m
1
m
2
−()u
1
2m
2
u
2
+
m
1
m
2
+
---------------------------------------------------------- -
u
2
′
m
2
m
1
−()u
2
2m
1
u
1
+
m
1
m
2
+
---------------------------------------------------------- -
u
1
′
u
2
′
u
1
′
u
2
′
