Tsoulfanidis N. Measurement and detection of radiation

Подождите немного. Документ загружается.

148

MEASUREMENT

AND

DETECTION

RADIATION

Equations giving the value of

have been reported by many

investigator^.'^-'^

The most recent equation reported by Forster et al.17 valid for

and

for

v/v,

2 is

A(Zl) exp

with

The proton stopping power is known.lg Brown19 has developed an equation of

the form

by least squares fitting the data of Northcliffe and

chilling."

The most recent

data are those of Janni4

The experimental determination of dE/h is achieved by passing ions of

known initial energy through a thin layer of a stopping material and measuring

the energy loss. The thickness Ax of the material should be small enough that

dE/h

AE/Ax. Unfortunately, such a value of Ax is so small, especially for

very heavy ions, that the precision of measuring Ax is questionable and the

uniformity of the layer has an effect on the measurement. Typical experimental

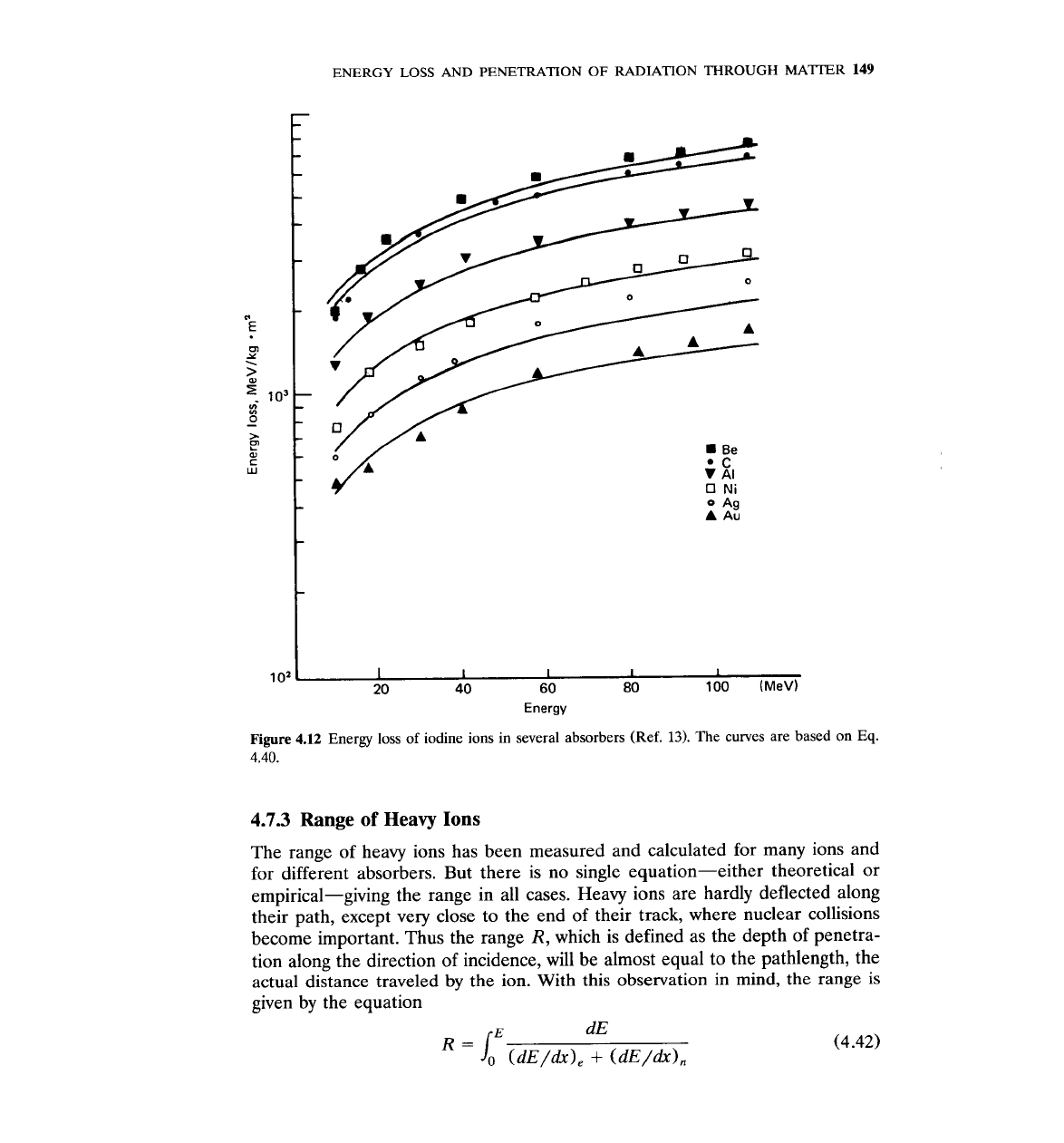
results of stopping power are presented in Fig. 4.12. The data of Fig. 4.12 come

from Ref. 13. The solid line is based on the following empirical equation

proposed by Bridwell and

BUC~"

and Bridwell and Moak2':

where

is the kinetic energy of the ion in MeV.

For a compound or mixture, dE/h can be obtained by using Eq. 4.12 with

(dE/d~)~ obtained from Eq. 4.36 or Eq. 4.40.

At velocities v

v,z,~/~, the energy loss through nuclear elastic collisions

becomes important. The so-called

nuclear stoppingpower

is given by the follow-

ing approximate expressionlo

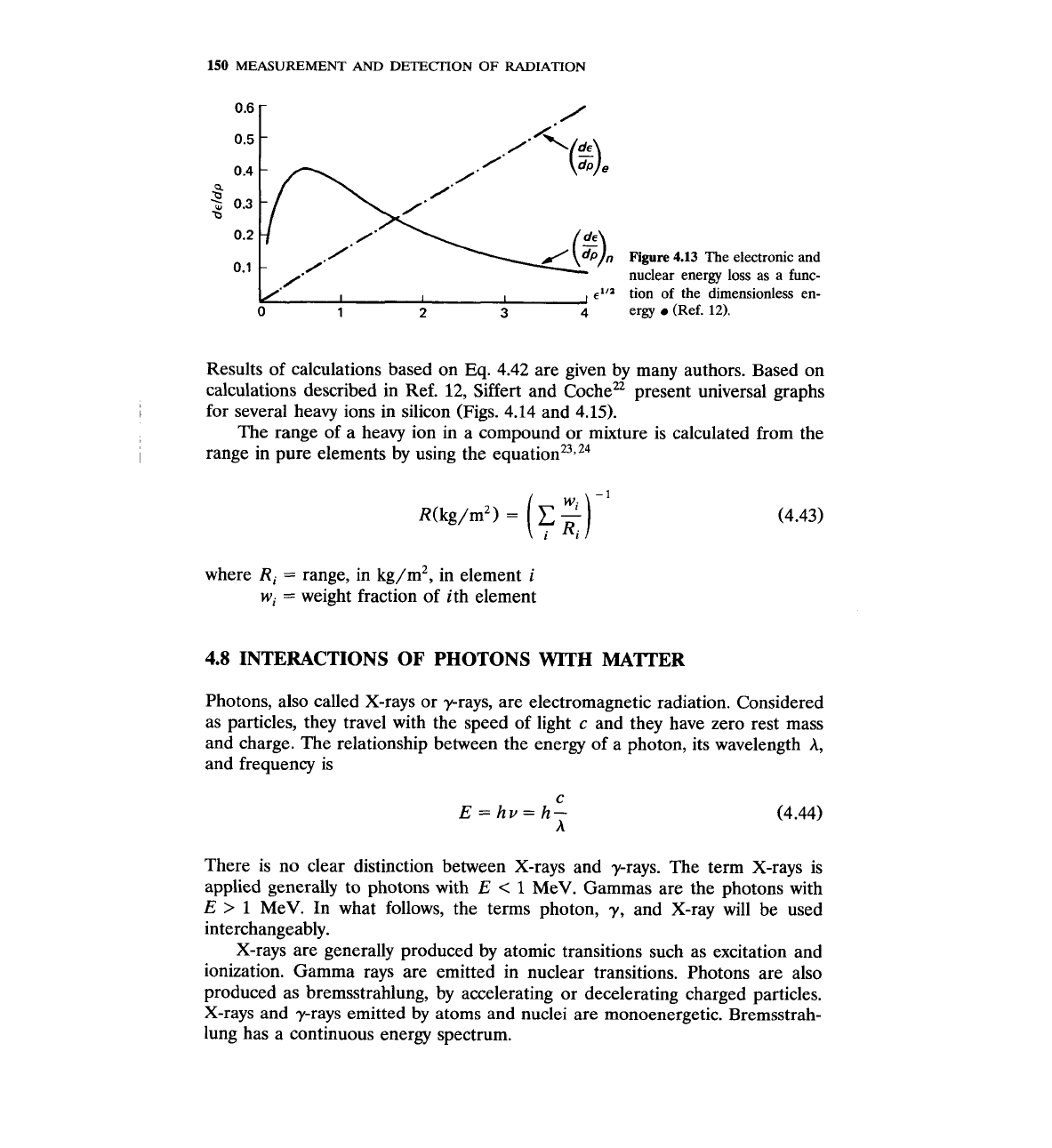
While the electronic stopping power

(d~/dp),

continuously decreases as the ion

speed

decreases, the nuclear stopping power increases as

decreases, goes

through a maximum, and then decreases again (Fig. 4.13).

ENERGY

LOSS

AND

PENETRATION

RADIATION

THROUGH

MA'ITER

149

lo2

20 40 60 80 100

(MeV)

Energy

Figure

4.12

Energy loss of iodine ions in several absorbers (Ref.

13).

The curves are based on Eq.

4.40.

4.7.3 Range of Heavy Ions

The range of heavy ions has been measured and calculated for many ions and

for different absorbers. But there is no single equation-either theoretical or

empirical-giving the range in all cases. Heavy ions are hardly deflected along

their path, except very close to the end of their track, where nuclear collisions

become important. Thus the range R, which is defined as the depth of penetra-

tion along the direction of incidence, will be almost equal to the pathlength, the

actual distance traveled by the ion. With this observation in mind, the range is

given by the equation

150

MEASUREMENT

AND

DETECTION

RADIATION

0.6

Figure

4.13

The electronic and

nuclear energy loss as

func-

I I

tion of the dimensionless en-

ergy

(Ref.

12).

Results of calculations based on

Eq.

4.42 are given by many authors. Based on

calculations described in Ref. 12, Siffert and ~oche" present universal graphs

for several heavy ions in silicon (Figs. 4.14 and 4.15).

The range of a heavy ion in a compound or mixture is calculated from the

range in pure elements by using the equati~n~~,~~

where

range, in kg/m2, in element

weight fraction of ith element

4.8

INTERACTIONS OF PHOTONS WITH MATI'ER

Photons, also called X-rays or y-rays, are electromagnetic radiation. Considered

as particles, they travel with the speed of light

and they have zero rest mass

and charge. The relationship between the energy of a photon, its wavelength A,

and frequency is

There is no clear distinction between X-rays and y-rays. The term X-rays is

applied generally to photons with

MeV. Gammas are the photons with

MeV. In what follows, the terms photon, y, and X-ray will be used

interchangeably.

X-rays are generally produced by atomic transitions such as excitation and

ionization. Gamma rays are emitted in nuclear transitions. Photons are also

produced as bremsstrahlung, by accelerating or decelerating charged particles.

X-rays and y-rays emitted by atoms and nuclei are monoenergetic.

Bremsstrah-

lung has a continuous energy spectrum.

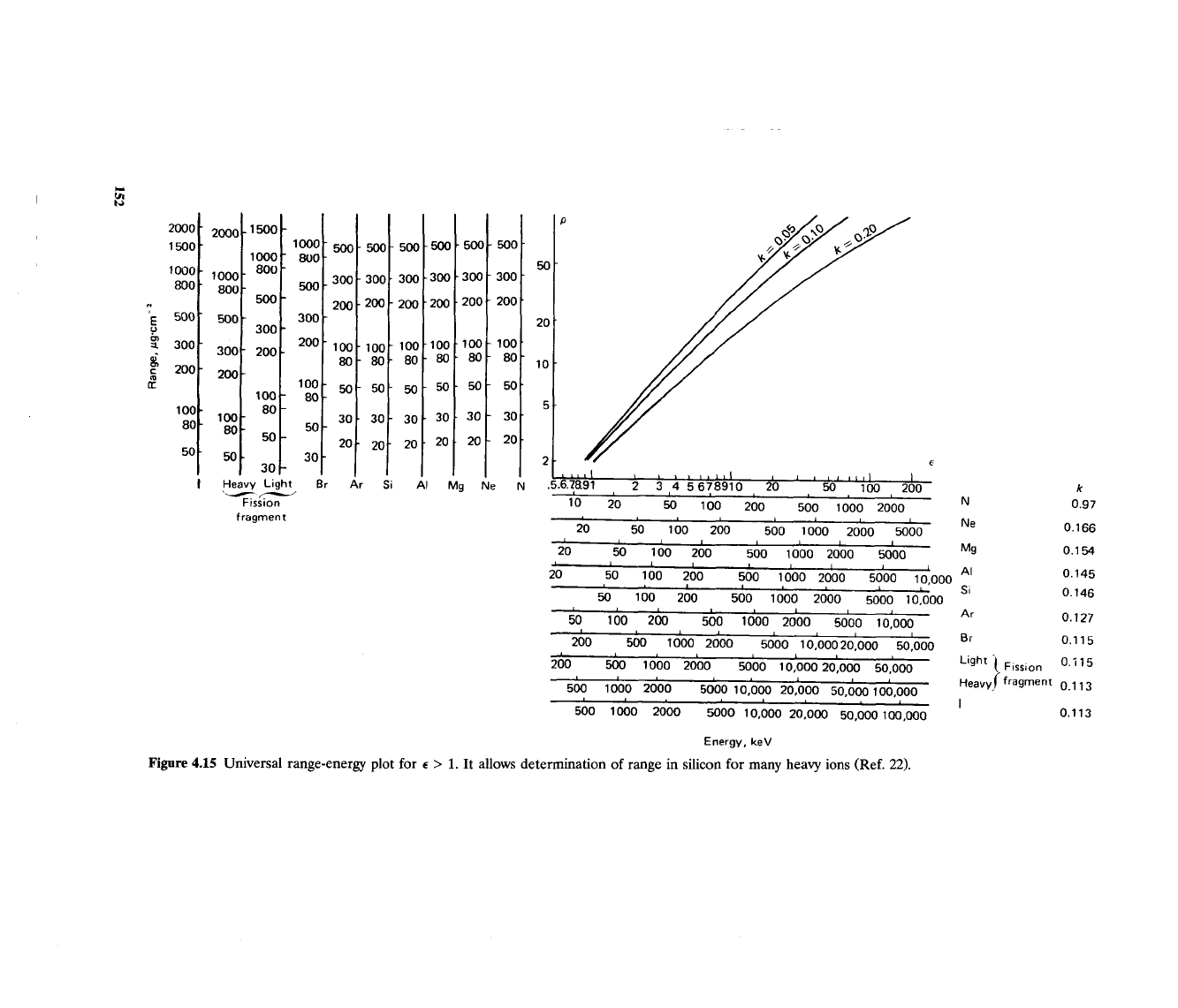
Figure

4.1

Heavy Light 8r

Fission

fragment

Universal range-energy plot

for

It allows

Energy,

keV

:termination of range in silicon for many heavy ions (Ref.

22).

0.115

Light

Flss,on

0.i 15

~eavy! fragment 0.1 13

0.113

ENERGY

LOSS

AND

PENETRATION

RADIATION

THROUGH

MATTER

153

There is a long list of possible interactions of photons, but only the three

most important ones will be discussed here: the photoelectric effect, Compton

scattering, and pair production.

4.8.1

The Photoelectric Effect

The photoelectric effect is an interaction between a photon and a bound atomic

electron. As a result of the interaction, the photon disappears and one of the

atomic electrons is ejected as a free electron, called the

photoelectron

(Fig. 4.16).

The kinetic energy of the electron is

(4.45)

where E,

energy of the photon

binding energy of the electron

The probability of this interaction occurring is called the

photoelectric cross

section

photoelectric coeficient.

Its calculation is beyond the scope of this

book, but it is important to discuss the dependence of this coefficient on

parameters such as E,, Z, and

The equation giving the photoelectric

coefficient may be written as

(m-')

aN-[I

O(Z)] (4.46)

E,"

where

probability for photoelectric effect to occur per unit distance traveled

by the photon

constant, independent of Z and E,

m, n

constants with a value of 3 to 5 (their value depends on E,; see

Evans)

have been defined in Sec. 4.3.

The second term in brackets indicates correction terms of the first order in

Figure 4.17 shows how the photoelectric coefficient changes as a function of E,

and Z. Fig. 4.17 and Eq. 4.46 show that the photoelectric effect is more

important for

high-Z material, i.e., more probable in lead

82)

than in

13). It is also more important for

10 keV than E,

500 keV (for the

same material). Using Eq. 4.46, one can obtain an estimate of the photoelectric

coefficient of one element in terms of that of another. If one takes the ratio of

for two elements, the result for photons of the

same energy

Figure

4.16 The photoelectric effect.

154

MEASUREMENT

AND

DETECTION

RADIATION

where

and

are density and atomic weight, respectively, of the two

elements, and

and

are given in m-'. If

and

are given in m2/kg, Eq.

4.47 takes the form

4.8.2

Compton

Scattering

Compton Effect

The Compton eflect is a collision between a photon and a free electron. Of

course, under normal circumstances, all the electrons in a medium are not free

but bound. If the energy of the photon, however, is of the order of keV or more,

while the binding energy of the electron is of the order of eV, the electron may

be considered free.

The photon does not disappear after a Compton scattering. Only its direc-

tion of motion and energy change (Fig. 4.18). The photon energy is reduced by a

certain amount that is given to the electron. Therefore, conservation of energy

gives (assuming the electron is stationary before the collision):

If Eq. 4.48 is used along with the conservation of momentum equations, the

energy of the scattered photon as a function of the scattering angle

can be

calculated. The result is (see Evans)

Using Eqs. 4.48 and 4.49, one obtains the kinetic energy of the electron:

cos 6)Ey/mc2

(1 -cos~)~~/mc~

matter of great importance for radiation measurement is the maximum

and minimum energy of the photon and the electron after the collision. The

minimum energy of the scattered photon is obtained when

This, of

course, corresponds to the maximum energy of the electron. From Eq. 4.49,

Ey',

min

2E,/mc2

photon energy and

(b)

atomic

(b)

number of the material.

ENERGY LOSS

AND

PENETRATION OF RADIATION THROUGH MATIER

155

e,T

freed

electron

Photon

+e--B---

Y, Ej

scattered photon

Figure

4.18

The

Compton effect.

and

The

maximum

energy of the scattered photon is obtained for

0, which

essentially means that the collision did not take place. From Eqs.

4.49

and 4.50,

The conclusion to be drawn from

Eq.

4.51 is that the minimum energy of the

scattered photon is greater than zero. Therefore,

in Compton scattering, it is

impossible for all the eneqy of the incident photon to be given to the electron.

The

energy given to the electron will be dissipated in the material within a distance

equal to the range of the electron. The scattered photon may escape.

Example

4.15

3-MeV photon interacts by Compton scattering. (a) What is

the energy of the photon and the electron if the scattering angle of the photon is

90"? (b) What if the angle of scattering is 180"?

Answer

(a) Using

Eq.

4.49,

E,=

0.437 MeV

0)3/0.511

0.437

2.563 MeV

(b) Using Eq. 4.51,

Eyl,

min

0.235 MeV

(2)3/0.511

0.235

2.765 MeV

Example

4.16

What is the minimum energy of the y-ray after Compton

scattering if the original photon energy is 0.511 MeV, 5 MeV, 10 MeV, or 100

MeV?

156

MEASUREMENT

AND

DETECTION

RADIATION

Answer

The results are shown in the table below (Eq. 4.51 has been used).

The probability that Compton scattering will occur is called the

Compton

coeficient

or the

Compton cross section.

It is a complicated function of the

photon energy, but it may be written in the form

where

probability for Compton interaction to occur per unit distance

f(EJ

a function of

If one writes the atom density

explicitly, Eq. 4.53 takes the form

In deriving Eq. 4.54, use has been made of the fact that for most materials,

except hydrogen,

22 to

2.62. According to Eq. 4.54, the probability

for Compton scattering to occur is almost independent of the atomic number of

the material. Figure 4.19 shows how

changes as a function of

and

If the

Compton cross section is known for one element, it can be calculated for any

other by using Eq. 4.53 (for photons of the same energy):

where

and

are given in m-'. If

and

are given in m2/kg, Eq. 4.55

takes the form

Figure

4.19

Dependence of the

Compton cross section on

(a)

photon energy and

(b)

atomic

(b)

number of the material.

ENERGY

LOSS

AND

PENETRATION

RADIATION

THROUGH

MATTER

157

4.8.3

Pair Production

Pair production is an interaction between a photon and a nucleus. As a result of

the interaction, the photon disappears and an electron-positron pair appears

(Fig. 4.20). Although the nucleus does not undergo any change as a result of this

interaction, its presence is necessary for pair production to occur.

y-ray will

not disappear in empty space by producing an electron-positron pair.+

Conservation of energy gives the following equation for the kinetic energy

of the electron and the positron:

Te+ T,+= E,

(mc21e- -(mc21e+

1.022 MeV (4.56)

The available kinetic energy is equal to the energy of the photon minus 1.022

MeV, which is necessary for the production of the two rest masses. Electron and

positron share, for all practical purposes, the available kinetic energy, i.e.,

Te-= Te+= +(E,

1.022 MeV)

(4.57)

Pair production eliminates the original photon, but two photons are created

when the positron annihilates (see

Sec. 3.7.4). These annihilation gammas are

important in constructing a shield for a positron source as well as for the

detection of gammas (see Chap. 12).

The probability for pair production to occur, called the pair production

coeficient or cross section is a complicated function of E, and

(see Evans and

Roy

Reed). It may be written in the form

where

is the probability for pair production to occur per unit distance traveled

and f( E,, Z) is a function that changes slightly with

and increases with E,.

Figure 4.21 shows how

changes with

and

It is important to note

that

has a threshold at 1.022 MeV and increases with E, and

Of the three

coefficients

and

being the other two),

is the only one increasing with the

energy of the photon.

'pair production may take place in the field of an electron. The probability for that to happen

is much smaller and the threshold for the gamma energy is

4mc2

2.04 MeV.

0.51

MeV

Figure

4.20

Pair production. The gamma disappears and a positron-electron pair is created. Two

0.511-MeV photons are produced when the positron annihilates.