Tsoulfanidis N. Measurement and detection of radiation

Подождите немного. Документ загружается.

138

MEASUREMENT

AND

DETECTION

RADIATION

The range of the 5-MeV deuteron (in air) is then (Eq. 4.20)

Example

4.10

What is the range of a 5-MeV deuteron in aluminum?

Answer

Using the Bragg-Kleeman rule (Eq. 4.17) and the result of the

previous example,

4.6.2

Range

of Electrons and Positrons

Electrons and positrons behave in essentially the same way with regard to

energy loss, slowing down, and penetration through matter. Small differences

exist; one was indicated when

dE/h

was discussed in Sec. 4.3. Small differences

in the values of the range between electrons and positrons should also be

expected, and indeed this is the case. Most of the range measurements have

been performed with electrons because electrons are used much more fre-

quently than positrons in radiation measurements. For this reason, from this

point on, only electrons will be discussed. The reader should be aware that the

results are equally applicable for positrons, to a first approximation, but for very

accurate results the references listed at the end of this chapter should be

consulted.

If the experiment shown in Fig. 4.5 and discussed in Sec. 4.6.1 is repeated

with the incident beam consisting of monoenergetic electrons, the result will

look as shown in Fig. 4.8. For electrons, the transmission curve does not have a

flat part. It decreases gradually to a level which is the background. The ranget is

equal to the thickness of the material, which is defined

the point where the

linear extrapolation of the transmission curve meets the background.

'1n many texts, this is called the "extrapolated" range. Since only one type of range is used,

there is no need to carry along the world "extrapolated."

Figure

4.8

The number of elec-

trons transmitted throub thick-

ness t. Experiment setup shown

Fig.

4.5.

ENERGY

LOSS

AND

PENETRATION

RADIATION

THROUGH

MA'ITER

139

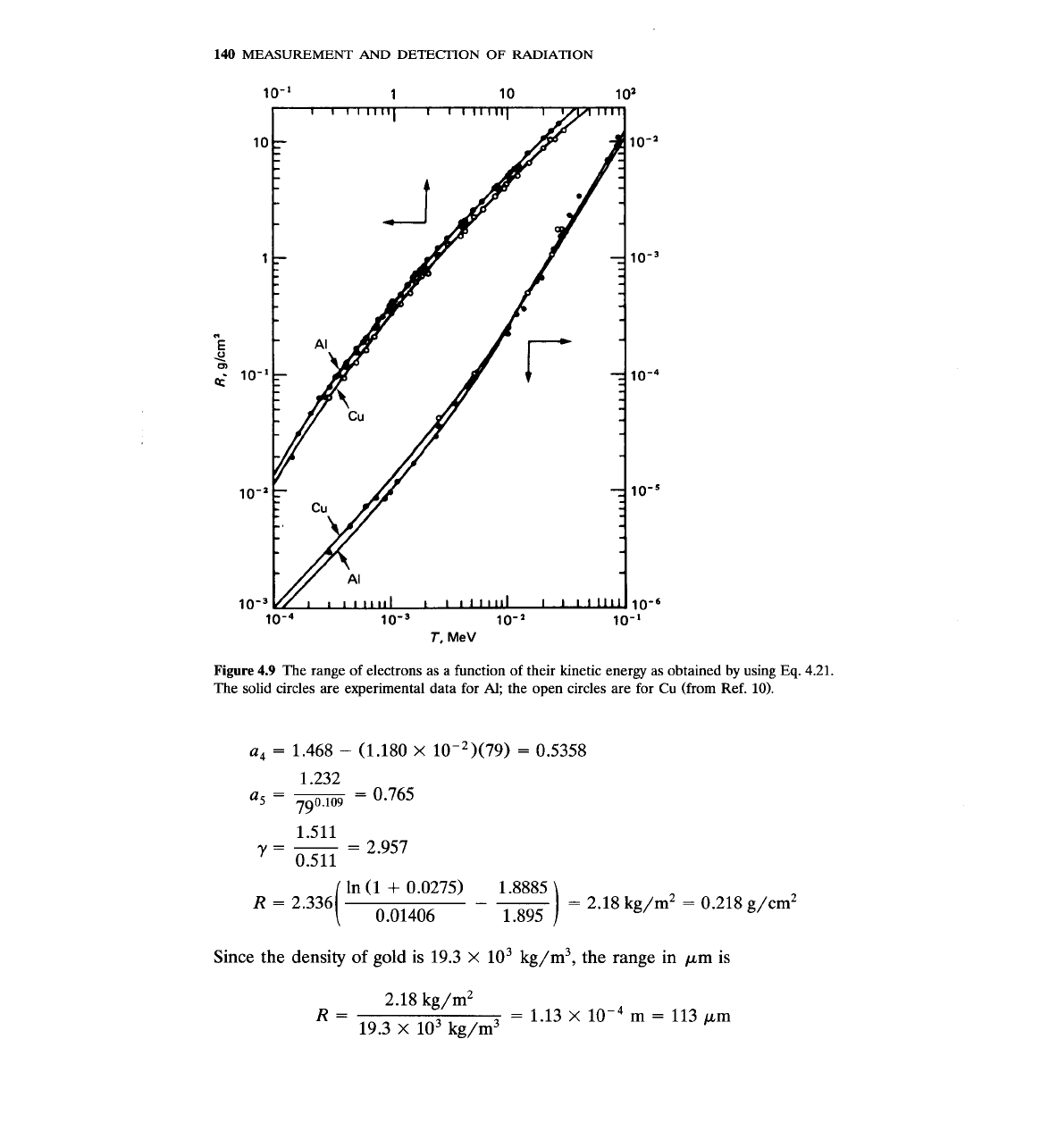
The semiempirical equation giving the range of electrons for the energy

range 0.3 keV to 30 MeV has been developed by Tabata, Ito, and Okabe,1°

based on the experimental results available until 1972. This equation, indicated

from now on as the TI0 equation, has the following form:

where

and

have been defined in Sec. 4.3.

Figures 4.9 and 4.10 show results based on

Eq.

4.21, as well as experimental

points.

In the case of absorbers that are mixtures or compounds, the atomic

number

and atomic weight

to be used in

Eq.

4.22 are given

z,,

wizi

where

is the weight fraction of element with atomic number

and atomic

weight

Ai.

Example

4.11

What is the range of 1-MeV electrons in gold?

79,

197.)

Answer

Using Eqs. 4.21 and 4.22,

140

MEASUREMENT

AND

DETECTION

RADIATION

lo-'

10 10'

MeV

Figure

4.9

The range of electrons as a function of their kinetic energy as obtained by using

Eq.

4.21.

The solid circles are experimental data for

Al;

the open circles are for Cu (from Ref.

10).

Since the density of gold is 19.3

lo3

kg/m3, the range in

ENERGY LOSS

AND

PENETRATION OF RADIATION THROUGH MATTER

141

MeV

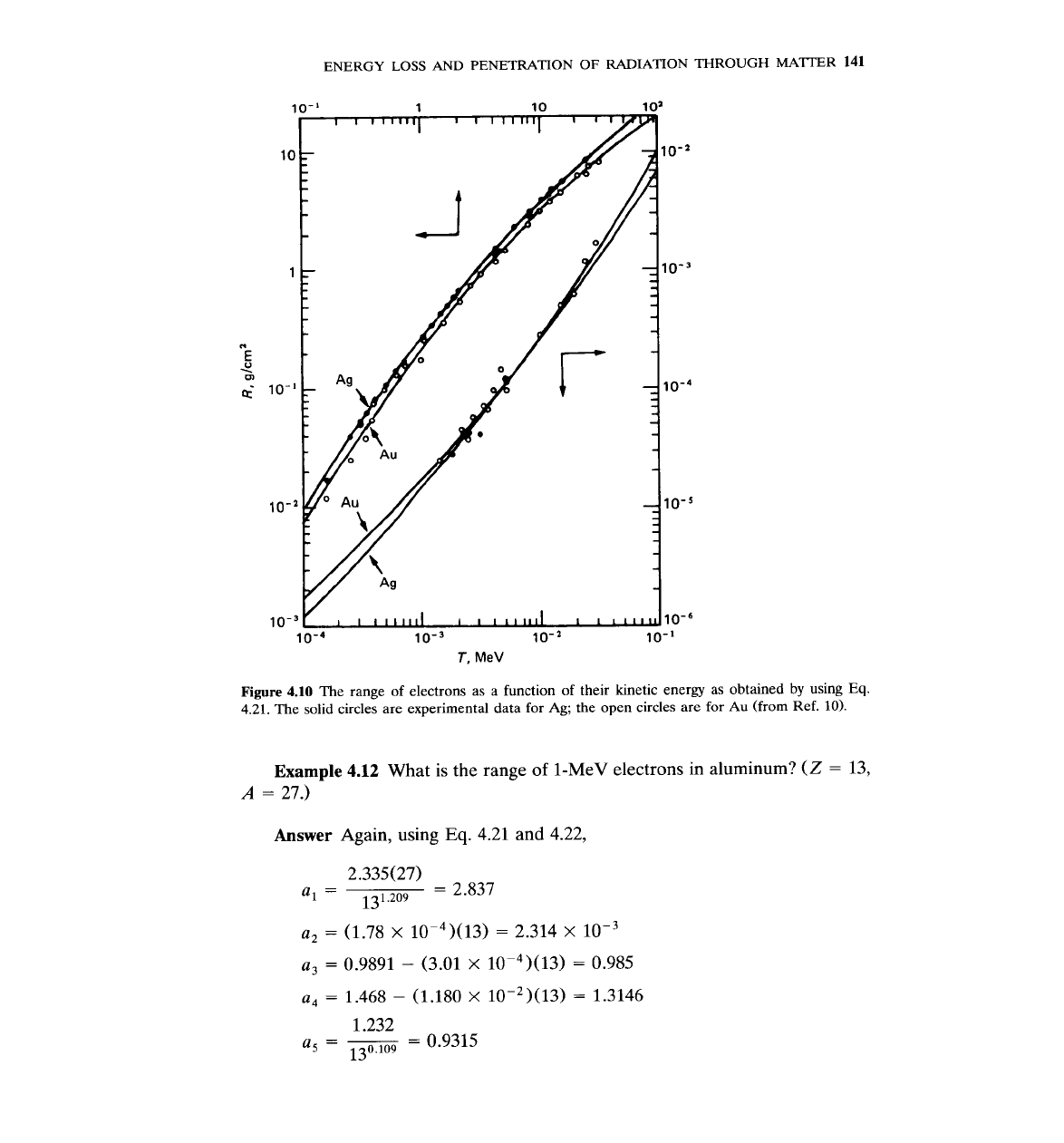
Figure

4.10

The range of electrons as a function of their kinetic energy as obtained by using

Eq.

4.21.

The solid circles are experimental data for Ag; the open circles are for

(from Ref.

10).

Example

4.12

What is the range

1-MeV electrons in aluminum?

13,

27.)

Answer

Again, using

Eq.

4.21 and 4.22,

142

MEASUREMENT

AND DETECTION OF

RADIATION

Since the density of aluminum is 2.7

lo3

kg/m3, the range in pm is

4.6.3 Transmission of Beta Particles

Beta particles have a continuous energy spectrum extending from zero energy

up to maximum kinetic energy

Em,,

(see Sec. 3.7.3). If the transmission experi-

ment shown in Fig. 4.5 is repeated with an incident beam of

particles, the

result will look as shown in Fig.

4.11.

The number of betas N(t) transmitted

through a thickness

is very closely represented by

N(t)

N(0)e-Wt (4.25)

where

is called the mass absorption coefficient.

The value of

has been determined experimentally as a function of the

maximum beta energy and is given by

Electron beam

,(monoenergetic)

Beta beam

Absorber thickness (relative units)

Figure

4.11

Transmission

betas.

corresponding curve for monoener-

getic electrons is also shown with

Emono

Emax.

ENERGY

LOSS

AND

PENETRATION OF RADIATION THROUGH

MATI'ER

143

where

Em,,

is in MeV. Notice that

is given in units of m2/kg; therefore the

thickness

in the exponent of Eq. 4.25 should be in kg/m2. The exponential

transmission law represented by

Eq.

4.25 is the result of experimental observa-

tion. There is no theory predicting it. The range of

particles is calculated

using Eq. 4.21 for kinetic energy equal to Em,,.

Example

4.13

What fraction of 2-MeV betas will go through a single

foil

of thickness 0.1 mm?

Answer

The mass absorption coefficient is, using Eq.

4.26.

The fraction transmitted is, using

Eq.

4.25,

N(t)

e-p'

exp [-0.7714 m2/kg(0.1

ml(2.7

lo3

kg/m3)1

N(0)

Therefore, 81 percent of the betas will go through this foil.

4.6.4

Energy Loss after Traversing a Material of Thickness

One is often required to calculate the energy loss of a charged particle after it

traverses a material of thickness

The first step in solving such a problem is to

calculate the range of the particle in that medium. If the range is

the

particle stopped in the medium and the total energy lost is equal to the initial

energy of the particle. If

the energy loss

is given by

where dE/& is the total stopping power (ionization-excitation plus radiation

loss). If t

one may take dE/& as constant and obtain

where (dE/dr), is the stopping power calculated for the initial energy of the

particle.

If the thickness

is a considerable fraction of the range, dE/& cannot be

considered constant. Then, Eq. 4.27 should be integrated using the appropriate

form of dE/&. Since the stopping power is a complicated expression, the

integration cannot be carried out by hand.

numerical integration can be

performed by a computer. In most cases, however, the following approach gives

adequate results.

144

MEASUREMENT AND DETECTION OF RADIATION

The thickness

is divided into

segments of length Axi, where

CAX~

Equation 4.27 takes the form

where (dE/d~)~ is the stopping power calculated for the kinetic energy of the

particle at the beginning of the segment Axi.

There is no general rule as to the best value of the number of segments

Obviously,

should be such that (dE/d~)~ changes by a small but acceptable

amount as the particle travels the segment Axi.

Example

4.14

What is the energy loss of a 10-MeV electron going through

15 mm of aluminum?

Answer

Using

Eq.

4.21 or Fig. 4.9, the range of a 10-MeV electron in

aluminum is

20.4 mm. The particle will emerge, but the thickness of the

absorber is a considerable fraction of the range. Therefore, one should use Eq.

4.29.

one chooses

5 and equal segments, Eq. 4.29 takes the form

The table below shows how the calculation proceeds.

Total energy loss is 7.958 MeV. Using

(dE/cix),, the energy loss would have

been equal to 0.605 MeV/mm

15mm

9.075 MeV, which is overestimated

by about 14%.

4.7 STOPPING POWER

AND

RANGE OF

HEAVY

IONS

4.7.1

Introduction

The equations presented in Secs. 4.3-4.6 for energy loss and range of charged

particles were derived with the assumption that the charge of the particle does

not change as the particle traverses the medium. This assumption is certainly

ENERGY

LOSS

AND

PENETRATION

RADIATION THROUGH

MATTER

145

valid for electrons, positrons, protons, and deuterons

1).

It holds well for

alphas too

2).

However, for

the charge of the particle cannot be

assumed constant, and for this reason the energy loss and range calculations

require special treatment.

Consider an atom or an ion with speed greater than the orbital velocity of

its own electrons. If this particle enters a certain medium, the atomic electrons

will be quickly removed from the atom or ion, leaving behind a bare nucleus.

The nucleus will keep moving through the medium, continuously losing energy

in collisions with the electrons of the

medium.+ It is probable that the ion will

capture an electron in one of these collisions. It is also probable that the

electron will be lost in another collision. As the ion slows down and its speed

becomes of the same order of magnitude as the orbital speeds of the atomic

electrons, the probability for electron capture increases, while the probability for

electron loss decreases. When the ion slows down even farther and is slower

than the orbiting electrons, the probability of losing an electron becomes

essentially zero, while the probability of capturing one becomes significant.

the speed of the ion continues to decrease, a third electron is captured, then a

fourth, and so on.

the end, the ion is slower than the least bound electron. By

that time, it is a neutral atom. What is left of its kinetic energy is exchanged

through nuclear and not electronic collisions. The neutral atom is considered as

stopped when it either combines chemically with one of the atoms of the

material or is in thermal equilibrium with the medium.

4.7.2

The

Calculation

The qualitative discussion of Sec.

4.7.1

showed how the charge of a heavy ion

changes as the ion slows down in the medium. It is this variation of the charge

that makes the energy loss calculation very difficult. There is no single equation

given

dE/&

for all heavy ions and for all stopping materials. Instead,

dE/&

calculated differently, depending on the speed of the ion relative to the speed of

the orbital electrons.

The stopping power is written, in general, as the sum of two terms:

where

(dE/cix),

electronic energy loss

(dE/dx),

nuclear energy loss

excellent review of the subject is presented by Northcliffe" and Lindhard,

Scharff, and Schiott." The results are usually presented as universal curves in

terms of two dimensionless quantities, the distance

and the energy

first

t~ollisions with nuclei are not important if the particle moves much faster than the atomic

electrons.

146

MEASUREMENT

AND

DETECTION OF RADIATION

introduced by Lindhard et al.1° and defined as follows:

wheret a

0.8853a,(~:/~

~,2/~)-'/~

actual distance traveled

h2/me2

Bohr radius

5.29

lo-''

Z,, MI

charge and mass of incident particle

Z2,

charge and mass of stopping material

The parameters N, r,, and mc2 have been defined in Sec. 4.3.

At high ion velocities,

V,Z?/~, where

e2/fi

orbital velocity of

the electron in the hydrogen atom, the nuclear energy loss is negligible. The

particle has an effective charge equal to Z,, and the energy loss is given by an

equation of the form

which is similar to

Eq.

4.2.

At velocities of the order of

u,z:/~, the ion starts picking up electrons

and its charge keeps decreasing. The energy loss through nuclear collisions is

still negligible.

In the velocity region

U,Z?/~, the electronic energy loss equation takes

the formlo

where

12.13

and

has a value very close to

The constant

depends on Z and

only,

not on energy, and its value is less than

Some typical values are given in Table

4.2.

Table 4.3 shows the kinetic energy per unit atomic mass, as well as the

kinetic energy, of several ions for

v,Z:/~.

The electronic stopping power for different ions and stopping materials is

obtained by using the following semiempirical approach.

se he

number

0.8853

(9.rr2)1/3/27/3 is called the Thomas-Fermi constant.

ENERGY LOSS

AND

PENETRATION OF RADIATION THROUGH MATIER

147

Table

4.2

Values of

Used in Eq.

4.34

The ratio of stopping power for two ions having the same velocity and

traveling in the same medium is given

(using

Eq.

4.33):

The application of

Eq.

4.35 to heavy ions should take into account the change of

the charge Z, as the ion slows down. This is accomplished

replacing Z, with

an effective charge,

Zeff

7721

where

is a parameter that depends on energy. The second particle in

Eq.

4.35

is taken to be the proton (Z,

I),

thus leading to the form14-l6

where the effective proton charge

77,

is given

Eq.

4.37, reported

Booth

rant'^,

and

is the proton kinetic energy in MeV:

77;

exp

150~,)]

exp (-0.835e-'~.~'~)

(4.37)

Table

4.3

The Kinetic Energy of Heavy Ions for Several

Values of

U,,Z~/~

voZ:'=

lo-')

Ion

(4s)

10')

T/A

T (MeV)