Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны
Подождите немного. Документ загружается.

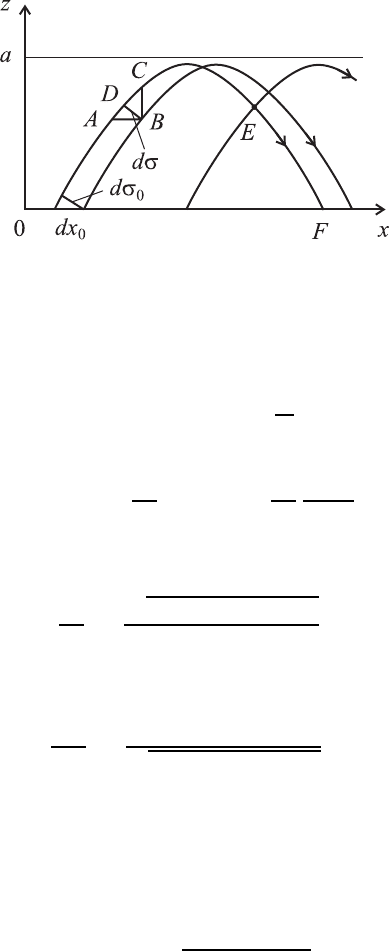
431
Рис. 17.12. К определению поля собственной моды методом
геометрической оптики
а при произвольных x и z из треугольника ABC можно записать |AB| =
= dx
0
, |BC| = dz = z(x + dx
0
) − z(x) =
dz
dx
dx
0
, |DB| = dσ. Отсюда
получаем
dσ = dz cos θ ≈
dz
dx
dx
0
cos θ =
dz
dx
cos θ
sin θ
0
dσ
0
.
Кроме этого, из уравнений (17.27) вытекает
dz
dx
=
p
n
2
(z) − n
2
m
cos
2
θ
0
n(z) cos θ
.
Собирая вместе все эти результаты, приходим к соотношению
dσ
0
dσ
=
n(z) sin θ
0
p
n
2
(z) − n
2
m
cos
2
θ
0
, . (17.43)
Следует также учесть, что через каждую точку в сердцевине волно-
вода проходит два луча — восходящий и нисходящий, уже коснувшийся
каустики. Для первого луча часть фазы, зависящая от координаты z,
равна
k
¯
ψ
1
(z) =
z
Z
0
p
k
2
n
2
(z
0
) − β
2
dz
0
Для нисходящего луча эту величину проще всего найти из соображений
симметрии. В точке F на рис.17.12 набег фазы вдоль луча равен половине

432
набега на период, т.е. π(N + 1/2). Двигаясь вдоль луча от этой точки в
обратном направлении, получаем, что в точке E пересечения двух лучей
фаза второго выражается соотношением
k
¯
ψ
2
(z) = π(N + 1/2) −
z
Z
0
p
k
2
n
2
(z
0
) − β
2
dz
0
Для обоих лучей слагаемое в фазе, пропорциональное x, равно βx. Уч и-
тывая это и подставляя формулы (17.37) и (17.43) в (17.24), получаем для
поля следующее выражение:
E(x, z) =
C e
−iβx
4
p
k
2
n
2
(z) − β
2
·
·
cos
z
R
0
p
k
2
n
2
(z
0
) − β
2
dz
0
, е сли N четное ;
sin
z
R
0
p
k
2
n
2
(z
0
) − β
2
dz
0
, если N нечетное .
(17.44)
где C — амплитудный множитель, конкретный вид которого несуще стве-
нен из-за линейности системы. Выражение (17.44) справедливо в области
между каустиками, положение которых определяется корнями уравнения
n
2
(z) = β
2
/k
2
. (17.45)
Точно на к аустике поле обращается в бесконечность, при этом условия
применимости приближения геометрической оптики оказываются нару-
шенными. Таким о бразом использованный метод не позволяет получить
решение, адекватно описывающее поле вблизи каустики и за ней. Для
получения такого решения исследуем более подробно распространение
электромагнитной волны в слоисто-неоднородной среде.
§ 4. Электромагнитные волны
в слоисто-неоднородной среде
Задачи о распространении волн в слоисто-неоднородной среде возни-
кают при изучении электромагнитных волн в плазме, радиоволн в ионо-
сфере Земли, звуковых волн в жидкости, волн нерегулярных волноводах,
в квантовой механике, а также во многих других задачах. Некоторые
примеры были уже рассмотрены в предыдущих параграфах этой главы.
Сейчас наша основная цель состоит в том, чтобы получить более точное
описание поля вблизи каустики, чем дает метод геометрической оптики.
433
Рассмотрим распространение электромагнитной волны в среде, ди-
электрическая проницаемость которой зависит только от координаты z:
ε = ε(z). Будем считать, что волновой вектор лежит в плоскости xz,
поэтому все компоненты поля не зависят от координаты y. Кроме того,
поскольку в направлении x среда однородная, то можно рассматривать
только решения, зависящие от x по гармоническому закону exp(−iβx),
где β — x-компонента волнового вектора. Таким образом в уравнениях
Максвелла (17.3a) и (17.3b) можно положить ∂/∂x = −iβ и ∂/∂y = 0.
Вид уравнения для поля зависит от поляризации волны. Возможны
два случая. Если вектор электрического поля перпендикулярен плоско-
сти падения xz, то компоненты поля E
x
, E
z
, и H
y
строго равны нулю. В
теории плоских диэлектрических волноводов собственные моды, обладаю-
щие такой поляризацией, называются T E-модами. Расписывая уравнения
(17.3a)и (17.3b) по координатам, получаем
H
x
=
1
−ik
dE
y
dz
, H
z
= −
β
k
E
y
,
dH
x
dz
+ iβH
z
= −ikεE
y
,
Подставляя первые два соотношения в третье, приходим к уравнению для
y-компоненты электрического поля:
d
2
E
y
dz
2
+ [k
2
ε(z) − β
2
] E
y
= 0 . (17.46)
Это уравнение совпадает с уравнением (17.5) из § § 1, которое было вы-
ведено для произвольной неоднородной среды в пренебрежении эффекта-
ми поляризации, если положить в (17.5) E(x, z) = E
y
(z) exp(−iβx). Мы
получили, что для T E-моды в плоско-слоистой среде уравнение (17.46)
является точным.
Аналогично, когда вектор электрического поля падающей волны ле-
жит в плоскости падения, выполняются соотношения H
x
= H
z
= E
y
= 0.
Моды с такой поляризацией называются T M-волнами. В этом случае из
уравнений Максвелла следует
E
x
=
1
iεk
dH
y
dz
, E
z
=
β
kε
H
y
,
dE
z
dz
+ iβE
z
= ikH
y
,
Все компоненты поля выражаются через одну скалярную функцию H
y
(z),

434
для которой получаем уравнение
d
dz
1
ε(z)
dH
y
dz
+
k
2
−
β
2
ε(z)
H
y
= 0 . (17.47)
Положим H
y
(z) =
p
ε(z)F (z), тогда уравнение для функции F (z) при-
обретает вид
d
2
F
dz
2
+
"
k
2
ε(z) +
ε
00
(z)
2ε(z)
−
3ε
0
2
(z)
4ε
2
(z)
− β
2
#
F (z) = 0 . (17.48)
Видно, что оно совпадает с уравнением (17.46), если ввести эффективную
диэлектрическую проницаемость ε
эфф
соотношением
k
2
ε
эфф
= k
2
ε +
ε
00
2ε
−
3ε
0
2
4ε
2
.
Если L — характерный масштаб изменения ε(z) то второе и третье слага-
емые имеют порядок ∆/(kL)
2
и ∆
2
/(kL)
2
по сравнению с первым. Здесь
2∆ = (ε
max
− ε
min
)/ε
max
— относительное изменение диэлектрической
проницаемости в среде, введенное по аналогии с высотой профиля пока-
зателя преломления для диэлектрических волноводов. Если kL 1, они
пренебрежимо малы, и можно считать ε
эфф
= ε. Для слабонаправляю-
щих диэлектрических волноводов, кроме того, высота профиля показате-
ля преломления мала: ∆ 1, поэтому уравнение для поля не зависит
от поляризации собственной моды с еще большей точностью. В результа-
те T M- и T E-моды слабонаправляющих волноводов оказываются выро-
жденными. Будет рассматривать, для определенности, уравнение (17.46),
используя для искомой компоненты поля обозначение F (z).
Пусть зависимость диэлектрической проницаемости среды от z имеет
вид, показанный на рис. 17.13. Предполагае тся, что волна распространя-
ется со стороны отрицательных значений z. Точка поворота z
0
, найденная
из уравнения (17.45), где n
2
= ε, разграничивает области с различным по-
ведением решения. Слева от этой точки функция q
2
(z) = k
2
n
2
(z)−β
2
> 0,
поэтому ВКБ-приближение для уравнения (17.46) равно
F (z) =
A
+
p
q(z)
exp
−i
z
Z
z
0
q(z
0
) dz
0
+
A
−
p
q(z)
exp
i
z
Z
z
0
q(z
0
) dz
0
,
(17.49)

435
Рис. 17.13. Зависимость диэлектрической проницаемости
от координаты вблизи точки поворота
где A
+
и A
−
— амплитуды волн, распространяющихся в положительном
и отрицательном направлениях оси x. Будем называть эти волны соответ-
ственно прямой и встречной. При z > z
0
имеем q
2
(z) < 0, в этом случае
ВКБ-решение равно
F (z) =
B
+
p
|q(z)|
exp
−
z
Z
z
0
|q(z
0
)|dz
0
. (17.50)
Это решение соответствует экспоненциально затухающей вглубь запре-
щенной области волне. Амплитуду второго линейно независимого реше-
ния, нарастающего вглубь запрещенной области, при заданных гранич-
ных условиях следует положить равной нулю. Действительно, если вол-
на падает слева, то в запрещенной области может существовать только
затухающая волна, иначе будет нарушен закон сохранения энергии. В
геометрической оптике точка z
0
является точкой положения каустики, в
квантовой механике она называется точкой поворота, так ка к ограничи-
вает классическое движение частицы в потенциальном поле .
В непосредственной окрестности точки поворота решениями (17.49)и
(17.50) пользоваться нельзя, так как здесь нарушаются условия примени-
мости ВКБ-приближения. Для построения решения в этой области вос-
пользуемся методом эталонных функций, суть которого можно выразить
словами: похожие дифференциальные уравнения имеют похожие реше-
ния
7
.
7
Для квантомеханической задачи об отражении частицы от потенциального барьера
этот метод излагается во многих учебниках по квантовой механике (см., например, [16,
17].)
436
Разложим вблизи точки поворота функцию q
2
(z) в ряд Тейлора: q
2
(z) =
= q
2
(z
0
)+(dq
2
/dz)
z=z0
(z −z
0
)+. . . ≈ k
2
ε
0
(z
0
)(z −z
0
) и введем безразмер-
ную координату ξ = k
2/3
|ε
0
(z
0
)|
1/3
(z − z
0
). Тогда вблизи точки поворота
вместо уравнения (17.46) можно записать
d
2
F
dξ
2
− ξF = 0 . (17.51)
Это уравнение называется уравнением Эйри, а его линейно независимые
решения называются функциями Эйри. Одна из этих функций обознача-
ется Ai(ξ) и ее можно представить в виде [2,18]
8
Ai(ξ) =
1
√
π
∞
Z
0
cos
t
3
3
+ ξt
dt . (17.52)
Функция Эйри хорошо изучена и протабулирована, а в современных ком-
пьютерных пакетах математического обеспечения, таких как Mathemat-
ica, она включена как стандартная функция. Нам потребуются асимпто-
тические разложения функции Эйри при больших значениях аргумен-
та [19]:
Ai(ξ) ∼
1
2ξ
1/4
exp( −
2
3
ξ
3/2
) , ξ > 0
Ai(ξ) ∼
1
|ξ|
1/4
cos(
2
3
|ξ|
3/2
−
π
4
) , ξ < 0
(17.53)
Как видно из этих формул, функция Эйри Ai(ξ) при больших положи-
тельных значениях аргумента экспоненциально убывает. Можно пока-
зать, что любое другое линейно независимое решение уравнения Эйри
в этом пределе будет экспоненциально возрастать, поэтому необходимое
нам решение выражается только через функцию Ai(ξ):
F (ξ) = CAi(ξ) . (17.54)
Здесь C — амплитудный множитель.
Предположим, что квазиклассическое приближение для уравнение
(17.46) становится применимым на таких расстояниях от точки поворота,
на которых функцию q
2
(z) все еще можно считать линейной. При таких
8
В широко распространенном справочнике [19] определение функции Эйри отличается
от приведенного здесь постоянным множителем. Вместо коэффициента 1/
√
π в [19] перед
интегралом стоит 1/π
437
значениях координаты можно сшить приближенные ВКБ-решения (17.49)
и (17.50) с решением (17.54). Определим условия, при которых процедура
сшивки возможна. Квадратичное слагаемое в разложении q
2
(z) в ряд Тей-
лора мало по сравнению с линейным, если |ε
0
(z
0
)||z−z
0
| |ε
00
(z
0
)||z−z
0
|
2
,
откуда, используя оценки ε
0
∼ ε/L и ε
00
∼ ε/L
2
, находим |z − z
0
| L.
Условие применимости ВКБ-приближения можно получить из формулы
(7.59), если заменить t на z и ω(t) на q(z): |q
0
(z)| |q
2
(z)|. В этом нера-
венстве можно использовать q
2
(z) ≈ k
2
ε
0
(z
0
)(z − z
0
), в результате чего
оно приводится к виду |z − z
0
| L/(
√
εkL)
2/3
. Таким образом, если вы-
полняется условие
√
εkL 1, всегда существует такое z
1
, для которого
одновременно выполняются неравенства
L
(
√
εkL)
2/3
|z
1
− z
0
| L . (17.55)
На расстояниях порядка z
1
от т очки поворота, с одной стороны, уже рабо-
тает ВКБ-приближение, а с другой — еще можно использовать уравнение
Эйри.
Предположим, что условие (17.55) выполнено. В этом случае ВКБ-
решения (17.49) и (17.50) должны совпадать с первым членом асимпто-
тического разложения решения (17.54). Вычислим интегралы в формулах
(17.49) и (17.50):
Z
z
z
0
q(z
0
)dz
0
≈
p
|ε
0
(z
0
)|k
Z
z
z
0
p
z
0
− z
0
dz
0
=
Z
|ξ|
0
p
ξ
0
dξ
0
=
2
3
|ξ|
3/2
,
если z < z
0
, и
Z
z
z
0
|q(z
0
)|dz
0
≈
p
|ε
0
(z
0
)|k
Z
z
z
0
p
z
0
− z
0
dz
0
=
Z
ξ
0
p
ξ
0
dξ
0
=
2
3
ξ
3/2
,
если z > z
0
. Подставляя эти выражения в (17.49) и (17.50) и сравнивая
полученные формулы с асимптотикой функции Эйри (17.53), получаем,
что коэффициенты A
+
, A
−
, B
+
и C связаны соотношениями
A
+
=
e
iπ/4
C
2
, A
−
=
e
−iπ/4
C
2
, B
+
=
C
2
. (17.56)
Эти формулы определяют связь между амплитудами падающей A
+
, отра-
женной A
−
и прошедшей в запрещенную область волны B
+
. Видно, что
коэффициент отражения от каустики равен A
−
/A
+
= exp(−iπ/2), то есть
по модулю амплитуды падающей и отраженной волн равны, а их фаза о т-
личается на −π/2. Это тот самый сдвиг фазы на каустике, о котором шла
речь в § § 1.
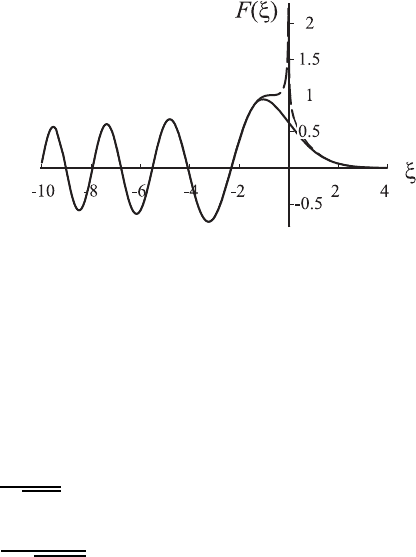
438
Рис. 17.14. Поле в плоско-слоистой среде вблизи каустики.
Пунктиром показаны ВКБ-решения (17.53).
Подставляя формулы (17.56) в (17.49) и (17.50), получаем, что искомое
решение имеет асимптотическое разложение
F (z)=
C
p
q(z)
cos
Z
z
z
0
q(z
0
) dz
0
− π/4
, z < z
0
, (17.57a)
F (z)=
C
2
p
|q(z)|
exp
−
Z
z
z
0
|q(z
0
)|dz
0
, z > z
0
. (17.57b)
В непосредственной окрестности точки поворота следует пользоваться
формулой (17.54). Подчеркнем, что найденное решение, и, следователь-
но, связь между амплитудами падающей, отраженной и проникающей
за к аустику волн, соответствует только заданным в физической поста-
новке задачи граничным условиям, когда из −∞ падает волна заданной
амплитуды, а справа от точки поворота есть только затухающая вглубь
запрещенной области волна. При других граничных условиях вид реше-
ния и соотношения между амплитудами будут другими. Более подробно
этот вопрос обсуждается в [2].
Найденное решение показано на рис. 17.14. В области z < z
0
оно имеет
вид стоячей волны, амплитуда которой увеличивается при приближении
к каустике, а расстояние между максимумами (локальная длина волны)
немного уменьшается. В области за каустикой (z > z
0
) поле экспоненци-
ально быстро спадает до нуля. В отличие от решения, полученного ме-
тодом геометрической оптики в предыдущем разделе, а также в отличие
от асимптотических выражений (17.57), поле остается конечным на кау-
стике. Главным максимум смещен в разрешенную область на величину,

439
определяемую формулой
z
m
− z
0
= −1,02 k
−2/3
|ε
0
(z
0
)|
−1/3
. (17.58)
На рис. 17.14 также показаны пунктиром ВКБ-решения (17.57). Видно,
что они являются очень хорошим приближением к точному решению при
всех z, кроме области шириной порядка |z
m
− z
0
|, непосредственно при-
мыкающей к каустике.
Можно считать, что в точке z
0
происходит полное отражение волны,
за каустику она практически не проникает. Положение точки отражения
определяется уравнением (17.45). Если угол падения волны на слоисто-
неоднородную среду равен нулю, то β = 0, и положение точки отражение
совпадает с нулем коэффициента преломления. Это условие выполняется,
например, в ионосферной плазме [20]. Если пренебречь затуханием и
магнитным полем Земли, то для диэлектрической проницаемости плазмы
можно записать
ε(z) = n
2
(z) = 1 −
4πe
2
N(z)
ω
2
m
, (17.59)
где N(z) — концентрация электронов в плазме, ω — частота. При верти-
кальном распространении волны в точке отражения получаем:
N(z) =
ω
2
m
4πe
2
= 1,24·10
−8
f
2
. (17.60)
Здесь частота должна быть выражена в гигагерцах, а концентрация в
см
−3
. Эта формула является основной для интерпретации данных по ра-
диозондированию ионосферы Земли и плазмы солнечной короны [20].
§ 5. Взаимодействие линейных волн в неоднородной среде
В приближении геометрической оптики различные волны не обме-
ниваются энергией. Чтобы показать это, рассмотрим, например, случай
акустической волны. Для прямой волны, бегущей в положительном на-
правлении оси z, комплексная амплитуда потенциала скорости равна
u(z) =
A
+
p
kn(z)
exp
−ik
z
Z
n(z
0
) dz
0
.
Подставляя это выражение в формулу (17.21) и дифференцируя, как это
следует делать в ВКБ-решениях, только экспоненциальный множитель,

440
для усредненного за период потока мощности волны получаем выражение
q = ωρ
0
|A
+
|
2
/2. Поскольку A
+
— константа, то поток мощности постоя-
нен вдоль оси z. Аналогично для потока мощности встречной волны, бе-
гущей в отрицательном направлении можно получить q = −ωρ
0
|A
−
|
2
/2,
т.е. также постоянную величину.
Чтобы учесть взаимодействие между волнами, необходимо выйти за
рамки ВКБ-приближения, учитывая следующие члены асимптотического
разложения. Однако, если функция n
2
(z) аналитическая, то можно пока-
зать, что взаимодействие прямой и встречной волны будет от сутствовать
в любом порядке асимптотического разложения — амплитуда отраженной
волны экспоненциально мала.
Можно поступить иначе, воспользовавшись другим методом, напри-
мер методом Ван-дер-Поля. Сделаем это на примере конкретной задачи
о переходном слое. Поставим задачу так: пусть есть слой ширины l, в
котором свойства среды плавно меняются. На границу z = 0 слоя пада-
ет волна с амплитудой A
+
(0) = A
0
; амплитуда встречной (отраженной)
волны на границе x = l равна нулю. Надо найти амплитуду A
−
(x) волны,
возникающей из-за о тражения от плавных неоднородностей, т.е. найти
амплитуду волны, распространяющейся справа налево. Введем новую пе-
ременную V = dF/dx и запишем для удобства (17.46) в виде системы
двух уравнений первого порядка:
dF
dz
= V ,
dV
dz
= −k
2
ε(z)F . (17.61)
Рассматривается одномерный случай, поэтому β = 0. Решение (17.61)
будем иск ать в виде (17.49), считая A
+
и A
−
функциями координаты, т.е.
F (z) =
A
+
(z)
4
p
ε(z)
e
−iϕ
+
A
−
(z)
4
p
ε(z)
e
iϕ
,
где
ϕ(z) = k
z
Z
0
p
ε(z
0
) dz
0
.
Так как вместо одной переменной F (z) мы ввели две новых A
+
(z) и
A
−
(z), то одно соотношение, связывающее эти новые переменные, можно
выбрать произвольно. Потребуем, чтобы
A
0
+
(z)
4
p
ε(z)
e
−iϕ
−
A
+
(z)ε
0
(z)
4
5
p
ε
5
(z)
e
−iϕ
+
A
0
−
(z)
4
p
ε(z)
e
iϕ
−
A
−
(z)ε
0
(z)
4
5
p
ε
5
(z)
e
iϕ
= 0 . (17.62)
