Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны

Подождите немного. Документ загружается.

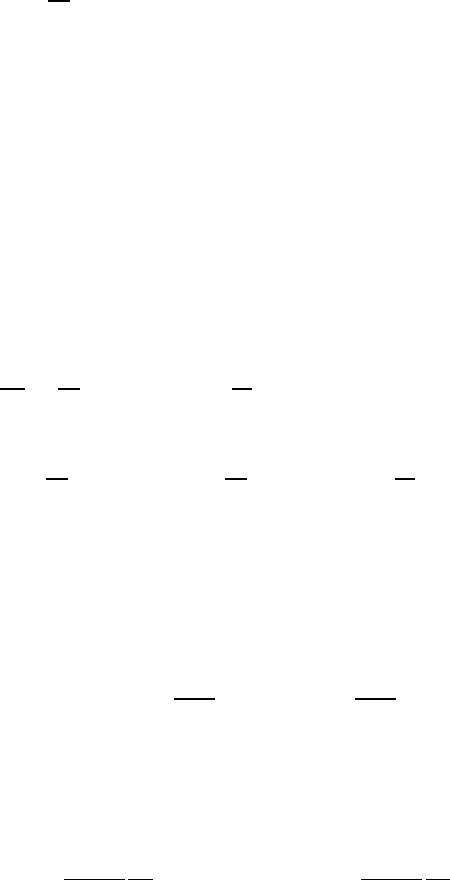
391

При выводе (16.14)-(16.16) мы не делали допущения о малости возму-

щений. Если же предположить, что v = v

+ v

, ρ = ρ

+ ρ

, j = j

+ j

= j

+ v

+ ρ

(возмущения много меньше соответствующих посто-

янных величин), то, сохраняя в (16.15) члены второго порядка малости,

получаем



+ 2v

+ v





+ 2v



. (16.17)

Рассчитаем среднюю за период плотность кинетической энергии для дрей-

фующего пучка, положив, что E

= E

пз

, и пучок лока льного возмущен

на входе высокочастотным сигналом частоты ω, а далее предоставлен са-

мому себе, т. е. в нем распространяются волны пространственного заряда,

в частности волны вида

пз

= E

пз

exp{i[ωt − (k + v

/ω

)x)] +

+ E

пз

exp{i[ωt − (k − v

/ω

)x)]

где E

пз

определяется начальным возмущением.

С учетом (16.17) имеем

i =

2π

d(ωt) +

2π

d(ωt) +

2π

d(ωt) +

2π

d(ωt) +

2π

d(ωt) . (16.18)

Первый интеграл — плотность энергии невозмущенного пучка, которую

мы обозначим hW

i. Поскольку v

и ρ

представляют собой суперпозицию

гармонических слагаемых (волн пространственного заряда), то второй и

четвертый интеграл равны нулю. Таким образом, нас интересует

δhW

i = hW

i − hW

i =

mρ

4πe

2π

d(ωt) +

2πe

2π

d(ωt) . (16.19)

Так как v

= (e/m)E

пз

/[i(ω − kv

)], а v

и ρ

для ω

 ω связаны соотно-

шениями (16.10), т о, вычисляя интегралы в (16.18), имеем для быстрой и

медленной волн пространственного заряда

δhW

пр. б

i ≈

пз

)

8π

> 0 , δhW

пр. м

i ≈ −

пз

)

8π

< 0 . (16.20)

392

Знак приближенного равенства появился потому, что в (16.20) мы прене-

брегли слагаемым, получившимся от вычисления первого интеграла, что

вполне оправдано при ω

 ω: это слагаемое в ω/ω

меньше второго.

Заметим, что если в (15.62) учесть, что E

пз

= −4πj

/(iω), и, следова-

тельно, j

∗

= ω

пз

/16π

, то приходим к (16.20).

Разумеется, и формула δhW

эл

i = (ω/16π)(dε/dω)|E

пз

с учетом того,

что dε/dω = ±2/ω

, приводит к тому же результату. При ω

 ω из

общих формул (16.4) имеем

б,м

= ±

, (16.21)

так как u = v

, v

= ±v

/ω.

Итак, отрицательной энергией обладают волны, в которых возмуще-

ния скорости и плотности противофазны. По-видимому, такое о бъяснение

возникновения воли с отрицательной энергией является достаточно о б-

щим; оно относится не только к электронике, но и ко многим гидродина-

мическим задачам, в которых принципиальна сжимаемость. Для несжи-

маемой жидкости столь просто интерпретировать физический смысл волн

с отрицательной энергией можно уже не всегда. В частности, если тече-

ние стратифицировано по плотности [13], то такое объяснение справедли-

во, при этом под возмущениями плотности следует понимать возмущения

градиента плотности. В случаях течений без стратификации, например в

пограничном слое, следует вести речь о волнах скорости и волнах давле-

ния [2,14].

Какие условия должны быть выполнены, чтобы в среде возникла вол-

на отрицательной энергии? Очевидно, для этого нужно, чтобы медленная

волна имела возможность отдавать некоторую часть своей энергии среде

или другим волнам.

Обратимся вновь к дисперсионному уравнению (15.33) в одномерном

случае. Если ввести потери в среде, то в дисперсионном уравнении воз-

никает малая мнимая часть, т. е. имеем

G(ω, k) + iν(ω, k) = 0

или

G(ω

, k) − iω

(ω

, k) + iν(ω

, k) = 0 ,

где ω = ω

−iω

. Из последнего уравнения сразу находим малую м нимую

добавку к невозмущенной частоте:

ν(ω

, k)

νa

. (16.22)

393

Очевидно, что знак энергии волны зависит от системы отсчета. При

преобразовании Галилея энергия волны преобразуется одновременно с

допплеровским сдвигом ее ч астоты. Величина L

= G

инвариантна

относительно преобразования Галилея, поэтому сдвигается лишь одна

граница волновых чисел, соответствующих ВОЭ, где ω = 0, а граница

= 0 остается неизменной.

Сам факт устойчивости или неустойчивости остается неизменным, а

соответствующий декремент или инкремент инвариантны. В соответствии

с формулой (16.22) функция ω

νa

меняет знак вместе с частотой волны.

Для неустойчивости ВО Э нужна “истинная” диссипация, т. е. положи-

тельные потери в лабораторной для ВОЭ системе отсчета. При движении

системы отсчета знаки энергии и потерь изменяются одновременно. Раз-

личие знаков энергии двух связанных волн также сохраняется в любой

системе отсчета.

Заметим, ч то при иной постановке задачи гармонический источник,

неподвижный относительно данной системы отсчета, возбуждает в среде

волну с частотой ω, и, следовательно, речь должна идти о пространствен-

ном усилении волны. Во спользуемся очевидным соотношением

+ G

= 0 ,

из которого следует, что

= −ω

гр

т. е. пространственный инкремент k

связан с временным ω

через груп-

повую скорость v

гр

. Изменение знака k

в области ω

< 0 не приводит к

усилению, поскольку при этом одновременно с k

меняется знак v

гр

, т. е.

направление потока энергии волны. Волна затухает в направлении рас-

пространения энергии. Пространственной неустойчивости соответствует

изменение знака k

одновременно с изменением знака ω

при неизмен-

ном знаке v

гр

. В окрестности точки, где L

= 0, нужно учесть следующий

член разложения G(ω, k) по k. Тогда

)

= 0



−



1/2

394

Рис. 16.2. Схема резистивного усилителя: 1 — резистивный

слой; 2 — диэлектрическая т рубка; 3 — электронный поток;

4 — входное и выходное устройства.

Таким образом, k

∼ (ω

)

1/2

. Проиллюстрируем сказанное о простран-

ственном усилении ВОЭ в среде с потерями на примере резистивного

усилителя [11] (рис. 16.2). Предварительно модулированный во входном

устройстве электронный пучок проходит через диэлектрическую трубку,

внутренняя поверхность которой покрыта поглощающим слоем, и наво-

дит в нем переменный заряд. Поля, создаваемые наведенными зарядами,

в свою очередь, воздействуют на электронный пучок и изменяют пере-

менную составляющую тока пучка. После прохождения трубки поток по-

падает в выходное устройство.

Входное воздействие возбуждает в пучке две волны пространственно-

го заряда, поля которых вызывают в резистивных стенках движущиеся

заряды; это в свою очередь приводит к джоулевым потерям энергии волн.

Но такие потери действуют по-разному на быструю и медленную волны.

Быстрая волна затухает (волна с положите льной энергией), а медленная

нарастает; отдавая энергию среде, последняя увеличивает свою амплиту-

ду. Экспериментальное доказательство нарастания медленной волны про-

странственного заряда в резистивном усилителе иллюстрирует рис. 16.3.

Сказанное легко подтвердить простой теорией, в основе которой лежат

линеаризованные уравнения

∂

∂x

+ 2i

∂j

∂x

−





iωρ

E , (16.23)

E = −

4π(j

+ j

ст

)

iω

= −

4πj

iω

−

4πσE

iω

, (16.24)

где j

ст

- плотность стороннего тока в поглощающем покрытии, σ - про-

водимость покрытия. Предполагая волновой характер проце ссов (j

, E ∼

exp[i(ωt−kx)]), из условия совместности уравнений (16.23) и (16.24) при-

395

|I|

äÁ

10.0

0.0

-10.0

-20.0

450 550 650 V ,B

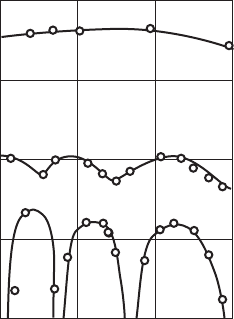
Рис. 16.3. Зависимость квадрата относительного сгруп-

пированного тока от ускоряющего напряжения [15]: 1 —

диэлектрическая среда заменена металлической поверхно-

стью (возбуждены две волны пространственного заряда с

постоянными амплитудами); 2 — пучок движется в рези-

стивной среде, но ток пучка мал (возбуждены нарастаю-

щая и затухающая волны); 3 — ток большой (преобладает

нарастающая медленная волна).

396

ходим к дисперсионному уравнению

(ω − kv

)

i4πσ

= 1 . (16.25)

Перепишем (16.25) в виде

(ω − kv

− ω

) (ω − kv

+ ω

) = i

4πσ (ω − kv

)

. (16.26)

Предположим далее, чт о ω −kv

≈ −ω

. Это соответствует возбуждению

медленной волны пространственного заряда. Тогда ω −kv

−ω

≈ −2ω

уравнение (16.26) становится таким: ω − kv

≈ −ω

− i2πω

/ω. Поэтому

k ≈

ω + ω

+ i

2πσω

, (16.27)

т. е. Re k равняется фазовой постоянной распространения медленной вол-

ны, a Im k = 2πσω/(ω

) > 0, и поэтому волна нарастает по мере рас-

пространения:

, E ∼ exp



−i

ω + ω

x +

2πσω



Аналогичные выкладки показывают, что быстрая волна пространственно-

го заряда будет затухать (проделайте эти расчеты самостоятельно).

Для поперечных электромагнитных волн энергия может быть отри-

цательна, например, в среде из двухуровневых частиц. Действительно, в

этом случае

ε = 1 −

− ω

+ 2iγω

, (16.28)

где ω

— частота перехода, ω

= 4πNd/m (d характеризует связь ча-

стицы с полем, N — концентрация частиц), N

= (n

− n

)/n

, n

1,2

—

заселенности нижнего и верхнего уровней [16]. Энергия волны на частоте

ω где ω − ω

 γ, приближенно пропорциональна

∂(ω

ε)

∂ω

= 2ω



1 + ω

− ω



(16.29)

и может быть отрицательной, если среда инвертирована — верхний уро-

вень заселен больше, чем нижний. Согласно (16.29) отрицательной будет

энергия волны при ω − ω

< ω

√

− n

/2. Ясно, что взаимодействие

волн с отрицательной энергией и волн с положительной энергией должно

сопровождаться неустойчивостью — обе волны будут расти по амплитуде.

397

§ 3. Связанные волны, синхронизм. Нормальный и аномальный эф-

фект Допплера

Ограничимся случаем слабой связи, когда феноменологический вывод

уравнений связанных волн элементарен. В отсутствие связи

= −ik

, (16.30)

где a

и a

нормированы так, что |a

и |a

— потоки мощности, пе-

реносимые волнами, k

и k

— постоянные распространения волн. Если

теперь связать волны, но считать связь слабой (k

и k

остаются такими

же, как и в отсутствие связи), т о

= −ik

+ c

= −ik

+ c

, (16.31)

где c

и c

— коэффициенты связи волн (c

и c

малы по сравне-

нию с k

и k

). Предположим далее, что затуханием волн можно прене-

бречь, т. е. в отсутствие связи k

1,2

= ω/v

1,2

— действительные величины,

1,2

—фазовые скорости несвязанных волн. В случае слабой связи общая

средняя мощность приближенно равна сумме мощностей в несвязанных

системах:

P = 2



±|a

± |a



≈ const ,

= 0 . (16.32)

Знаки “+” и “−” соответствуют волнам с положительной и отрицательной

энергией.

В том случае, когда одна из волн - волна пространственного заряда в

электронном потоке, а другая - электромагнитная волна в замедляющей

системе, (16.32) как раз и есть математическое выражение теоремы Чу

в теории электронных СВЧ-приборов с длительным взаимодействием в

так называемом двухволновом приближении [17, 18]. В частности, для

дрейфующего электронного пучка теорема Чу о кинетической мощности

имеет вид P = 2(|a

− |a

) = const.

Поскольку |a|

= aa

∗

, из второй формулы в (16.32) следует, что

= ±



∗

+ a

∗





∗

+ a

∗



= 0 . (16.33)

Подставляя (16.31) и комплексно-сопряженные им уравнения в (16.33)

находим

(±c

∗

± c

∗

+ (±c

± c

∗

= 0 . (16.34)

398

Соотношения (16.34) справедливы для любых a

и a

, поэтому

= ±c

∗

при P = ±|a

+ |a

, (16.35)

= ∓c

∗

при P = ±|a

− |a

, (16.36)

(16.37)

Считая, что a

, a

∼ exp[i(ωt − kx)] и принимая во внимание форму-

лы (16.35) и (16.36), из условия совместности уравнений (16.31) получаем

следующие дисперсионные уравнения:

1) для одинаково направленных потоков мощности (одинаковые знаки

перед |a

и |a

в первой из формул (16.32)):

(k − ω/v

) (k − ω/v

) = |c

. (16.38)

2) для противоположно направленных потоков мощности (разные зна-

ки перед |a

и |a

(k − ω/v

) (k − ω/v

) = −|c

. (16.39)

В системе без потерь возможны четыре варианта связи взаимодейству-

ющих волн (табл. 16.1, взятая из [19]). Дисперсионные характеристики

несвязанных волн представлены штриховыми линиями, а сплошные ли-

нии соответствуют возможным вариантам связи.

Проиллюстрируем таблицу конкретными примерами из высокочастот-

ной электроники, основываясь на теории взаимодействия прямолинейно-

го электронного потока с бегущей электромагнитной волной (см. гл. 14).

Обратимся к уравнению возбуждения волноведущей системы током элек-

тронного пучка:

∂E

∂x

+ i

E = −





K I (16.40)

и к уравнению для тока, сгруппированного в пучке под действием поля

волноведущей системы:

∂

∂x

+ 2i

∂I

∂x

−

− ω

I = i

E . (16.41)

399

Таблица 16.1.

ω − k диаграмма Свойства системы связанных

волн

Примеры систем связанных

волн

k — действительная величи-

на для всех ω и наоборот;

неустойчивости нет

Связь двух волн с положи-

тельной энергией или двух

волн с отрицательной энерги-

ей

ω — действительная величина

для всех k; k — комплексная

величина для действительных

значений ω; волны, затухаю-

щие в пространстве; неустой-

чивости нет

то же

k — комплексная величина

для действительных значений

ω и наоборот; k имеет значе-

ние, соответствующее усиле-

нию, для действительных ω;

конвективная неустойчивость

Связь волны с положительной

энергией с волной с отрица-

тельной энергией; групповые

скорости волн имеют одно на-

правление

k — действительная величи-

на для всех действительных

ω; ω — комплексная величи-

на для действительных k; аб-

солютная неустойчивость

Связь волны с положительной

энергией с волной с отрица-

тельной энергией; групповые

скорости волн противополож-

ны по направлению

400

Если I(0) = 0 и (∂I/∂x)

x=0

, то (16.41) можно переписать в виде

I(x) =

E(ζ) exp[−i(k

− k

)(x − ζ)] dζ −

−

E(ζ) exp[−i(k

+ k

)(x − ζ)] dζ = I

(x) + I

(x) , (16.42)

где k

= ω/v

, k

= ω

, индексы “м” и “б” соответствуют интегралам,

связанным с возбуждением медленной и быстрой волн пространственного

заряда. Тогда вместо (16.41) или (16.42) можно написать два уравнения

первого порядка:

∂I

∂x

+ i(k

+ k

= −

E(x) , (16.43)

∂I

∂x

+ i(k

− k

E(x) . (16.44)

Условия для резонансного взаимодействия

+ k

= k

= ω/v

или v

1 + ω

/ω

(16.45)

соответствуют условиям синхронизма электромагнитной волны в замед-

ляющей системе и быстрой волны пространственного заряда в пучке, а

условия

− k

= k

= ω/v

или v

1 − ω

/ω

, (16.46)

соответствуют условиям синхронизма волны в замедляющей системе и

медленной волны пространственного заряда. При выполнении условий

(16.45) или (16.46) в системе уравнений (16.40), (16.43) и (16.44) можно

вместо трех уравнений оставить только два. В этом случае возможны сле-

дующие взаимодействия (см. табл. 16.1) и соответствующие им приборы:

1) Взаимодействие быстрой волны пространственного заряда с пря-

мой волной в волноведущей структуре (обе волны с положительной

энергией); групповые скорости направлены в одну сторону; ЛБВ-

подавитель; при определенных значениях постоянного тока пучка и

ускоряющего напряжения для данной частоты имеет место полное

подавление входного сигнала.