Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны

Подождите немного. Документ загружается.

371

Когда L содержит производные функции ϕ второго или более высокого

порядка, то уравнение, которое называют уравнением Эйлера имеет вид:

−

∂

∂t

−

∂

∂x

ϕ,j

∂

∂t

∂

∂t∂x

∂

∂x

ϕ,jk

−. . . = 0 .

(15.23)

Уравнение (15.23) является результатом повторного интегрирования по

частям.

Уравнения (15.22) и (15.23) — уравнения в частных производных для

ϕ(x, t), причем уравнениям такого вида можно дать эквивалентную вари-

ационную формулировку.

В качестве типичного примера для дальнейшего построения теории

вновь используем уравнение Клейна-Гордона в виде:

− α

∇

ϕ + β

ϕ = 0 . (15.24)

Сравнивая уравнения (15.24) и (15.22), находим выражение для лагран-

жиана

L =

−

(∇ϕ)

−

. (15.25)

Как уже использовалось для медленно меняющихся волновых паке тов

ϕ ∼ Re[A exp(iθ)], т.е.

ϕ ∼ a cos(θ + η) , (15.26)

где a = |A|, η = Arg A, ω = ∂θ/∂t, k

= −∂θ/∂x

. Подставим (15.26)

в лагранжиан, пренебрежем производными от a, η, ω и k и проведем

усреднение по периоду, т.е. перейдем к

L(a, ω, k) =

2π

L dθ .

Тогда для уравнения Клейна-Гордона (15.24), используя соотношения (15.25)

и (15.26), получим:

L =



− α

− β



. (15.27)

372

Задача 15.1. Докажите, что для уравнений

− α

∇

ϕ = β

∇

+ γ

xxxx

= 0 ,

с дисперсионными уравнениями ω = ±iαk/

1 + β

, и ω = ±γk

спра-

ведливы соотношения

L =



− α

+ β



L =



− γ



Постулируем теперь усредненный вариационный принцип

L(+θ

, −θ

, a) dtdx = 0 (15.28)

для функций θ(x, t) и a(x, t).

Поскольку производные от a от сутствуют, уравнение Эйлера (15.23)

для вариации функции a имеет вид

δa : L

= 0 .

Вариационное уравнение для функции θ таково:

δθ :

∂

∂t

∂

∂x

θ,j

= 0 .

В эти соотношения входят только производные по θ, поэтому снова удоб-

нее вернуться к ω, k и a. Тогда условия совместности, необходимые для

существования фазы, выглядят так:

= 0 , (15.29)

∂

∂t

−

∂

∂x

= 0 , (15.30)

∂k

∂t

∂ω

∂x

= 0 ,

∂k

∂x

−

∂k

∂x

= 0 . (15.31)

Уравнение (15.29) ничем, кроме дисперсионного уравнения быть не мо-

жет, поскольку является функциональным соотношением между ω, k и

a, что легко проверить во всех примерах задачи 15.1.

Тогда очевиден следующий важный вывод. Для любой линейной за-

дачи лагранжиан L есть квадратичная функция от ϕ и ее производных.

Как следствие этого, выражение для L имеет следующий вид:

L = G(ω, k) a

. (15.32)

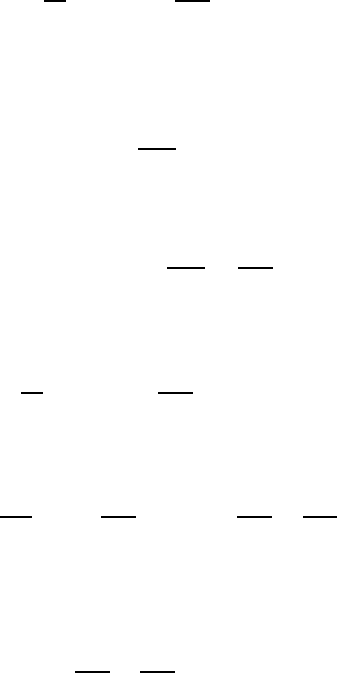
373

Тогда, согласно соотношению (15.29) дисперсионное уравнение должно

иметь вид

G(ω, k) = 0 , (15.33)

и функция G(ω, k) в L — не что иное, как дисперсионная функция (см.

(15.27) и формулы для L в задаче 15.1. Таким образом, в каждом случае

не нужно даже вычислять L: ее структура ясна.

Перепишем амплитудное уравнение (15.30), используя соотношение

(15.32), так:

∂

∂t





−

∂

∂x





= 0 . (15.34)

Из уравнения (15.33) следует, ч то ω = W (k), поэтому равенство G[W (k), k] =

= 0 выполняется т ождественно. Следовательно

∂W

∂k

+ G

= 0

и групповая скорость

гр j

∂W

∂k

. (15.35)

Пусть G

(W, k) = g(k). Тогда уравнение (15.34) принимает вид:

∂

∂t



g(k)a



∂

∂x



g(k)v

гр j



= 0 . (15.36)

Из соотношений (15.31) следуе т, что

∂k

∂t

+ v

гр j

∂k

∂x

= 0 ,

∂k

∂x

−

∂k

∂x

= 0 .

Используя последние соотношения, исключим из уравнения (15.36) функ-

цию g(k), что дает

∂a

∂t

∂

∂x



гр j



= 0 .

Ранее мы получили аналогичное уравнение (второе из (15.18)), где усред-

ненная пло тность энергии представлялась в виде E = F (k)a

. Однако,

374

функции F (k) и g(k) не совпадают, поэтому нельзя считать, что соотно-

шение (15.36) представляет собой усредненное энергетическое уравнение

— первое уравнение из (15.18).

Для дальнейших рассуждений Уизем [3] привлекает теорему Нетер,

которая утверждает, ч то каждой группе преобразований, относительно

которой лагранжиан инвариантен, соответствует свое уравнение сохране-

ния. Если лагранжиан инвариантен относительно сдвига по t, это утвер-

ждение к нему применимо, и соответствующее энергетическое уравнение

оказывается таким:

∂

∂t

(ωL

− L) +

∂

∂x



−ωL



= 0 . (15.37)

Лагранжиан в (15.28) удовлетворяет указанному требованию инва-

риантности. Вслед за Уиземом не будем прослеживать во всех деталях

применение теоремы Нетер, а лишь укажем, что соотношение (15.37) по-

лучается из системы уравнений (15.29)-(15.31) (предоставляем читателю

убедиться в этом самому).

Как показано выше, в линейном случае стационарное значение L = 0,

поэтому для плотности энергии имеем

E = ωL

, (15.38)

а для плот ности потока энергии

= −ωL

. (15.39)

Следовательно, L

= E/ω, и уравнения (15.30) или (15.37) можно запи-

сать в виде:

∂

∂t





∂

∂x



гр j



= 0 , (15.40)

а из формул (15.32), (15.38) и (15.39) имеем E = ωG

и F

= v

гр j

E = −

−ωG

. Напомним, что величина E/ω уже встречалась нам в главе 7 где

она интерпретировалась как адиабатический инвариант для осциллятора

с медленно изменяющимися параметрами.

Задача 15.2. Известно, что усредненный гамильтониан, т.е. плотность энер-

гии волны, выражается как

H =

p ˙q −

L ,

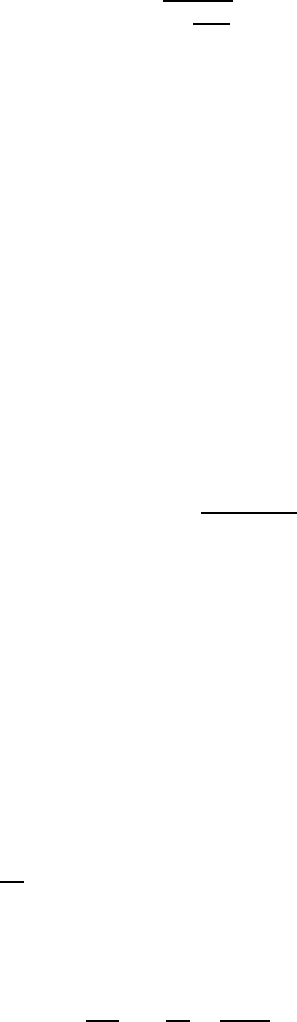
375

где p = L + ϕ

, ˙q = ϕ

, а плотность потока энергии как

S =

˙q

∂L

∂q

(черта означает усреднение за период).

Полагая для про стоты, что ϕ(x, t) = a(x, t) cos θ(x, t) , докажите следу-

ющие соотношения:

H = ωL

− L , S = −ωL

§ 3. Плотность энергии электромагнитного поля в среде с диспер-

сией

Метод М.Л.ЛевинаНачнем с примера изящного вывода выражения для

средней плотности электромагнитной энергии в непоглощающей диспер-

гирующей среде, принадлежаще го М.Л. Левину, следуя книге [4].

Предположим, что вещество с диэлектрической проницаемостью ε(ω)

и магнитной проницаемостью µ(ω) заполняет плоский конденсатор с ем-

костью C = ε(ω)C

и тонкий соленоид с индуктивностью L = µ(ω)L

(рис. 15.1). Конденсатор и соленоид соединены в колебательный контур,

в котором при отсутствии потерь могут возникнуть свободные гармони-

ческие колебания с частотой ω

= 1/

L(ω)C(ω). Введем теперь в контур

в некоторый момент времени сопротивление R. Понятно, что, начиная с

этого момента, колебания начнут затухать, а первоначально запасенная

электромагнитная энергия будет переходить в джоулево тепло, которое

выделяется на сопротивлении R. Поэтому полное количество тепла, вы-

делившееся в сопротивлении R за время, когда колебания прекратятся,

будет равно электромагнитной энергии, запасенной в контуре до введения

сопротивления. Таким образом, решение поставленной задачи сводится к

вычислению джоулева тепла.

Допустим, что при t < 0 в контуре имеют место свободные колебания,

так что сила тока в контуре I = I

iωt

, а напряжение на обкладнах

конденсатора V = V

iωt

. Ток и напряжение связаны уравнением

+ V = 0 или iωLI + V = 0 ,

Начиная с момента t = 0, когда в контур введено сопротивление R, коле-

бания будут описываться уравнением

L(˜ω)

+ R

C(˜ω)

= 0 ,

376

Рис. 15.1. Колебательный контур LRC. C

и L

— значе-

ния емкости и индуктивности, когда в пространстве между

обкладками конденсатора и внутри соленоида вакуум; ес-

ли R = 0, то ω

= 1/

L(ω)C(ω) — частота свободных

гармонических колебаний.

решение которого для t > 0 есть T = I

exp(i˜ωt), где ˜ω — комплексная

частота, определяемая характеристическим уравнением

˜ωL(˜ω) −

˜ωC(˜ω)

= iR . (15.41)

Если R → 0, то ˜ω → ω, а ω удовлетворяет характеристическому уравне-

нию

ωL(ω) −

ωC(ω)

= 0 . (15.42)

Вычтем из уравнения (15.41) уравнение (15.42) и после простых преобра-

зований заменим все разности дифференциалами. Тогда

˜ωL(˜ω) − ωL(ω) −



˜ωC(˜ω)

−

ωC(ω)



= iR −→

−→



˜ωL(˜ω) − ωL(ω)

˜ω − ω

˜ωC(˜ω) − ωC(ω)

˜ω − ω

˜ωωC(˜ω)C(ω)



= iR −→

−→



d(ωL)

dω

d(ωC)

dω



(˜ω − ω) = iR .

Полагая ˜ω = ω + iδ, находим

d(ωL)

dω

d(ωC)

dω

. (15.43)

Чтобы найти джоулево тепло, надо проинтегрировать выражение R

по времени, учит ывая, что

I → Re I =

(I + I

) .

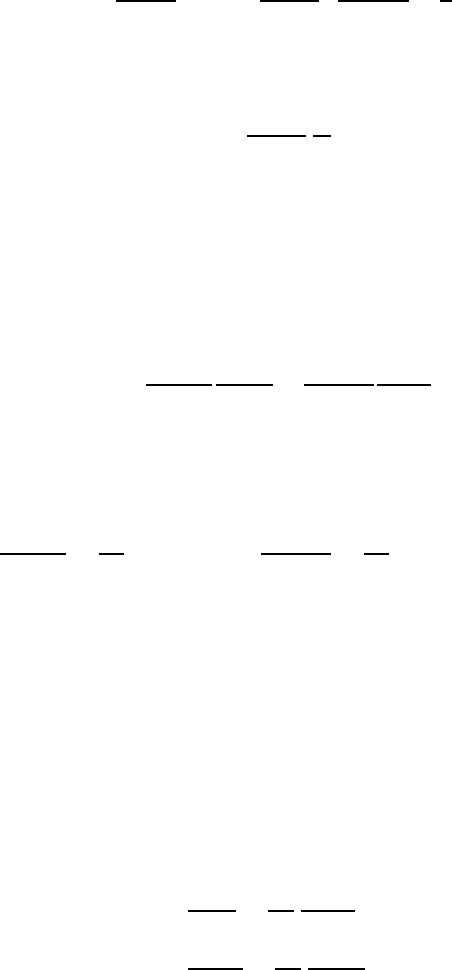
377

Энергия, первоначально запасенная в колебательном контуре, равна

W =

∞



I + I



dt =

R|I



+ δ



(15.44)

или в пределе при δ → 0

W =

R|I

. (15.45)

Задача 15.3. Докажите соотношение (15.44), используя, что I = I

exp(i˜ωt)

и V = V

exp(i˜ωt).

Подставляя в формулу (15.45) выражение (15.43) и пользуясь соотно-

шением ωL|I

| = |V

|, находим

W =

d(ωµ)

dω

d(ωε)

dω

. (15.46)

В случае, когда между обкладками конденсатора и внутри соленоида был

вакуум, для средних по времени значений магнитной и электрической

энергий справедливы соотношения:

8π

, (15.47)

где v

и v

— объемы соленоида и конденсатора, а E и H — векторы

напряженности электрического и магнитного полей, когда амплитуды на-

пряжения на конденсаторе и тока в соленоиде равны V

и I

, знак hi

означает усреднение по времени.

Поскольку при зада нных V

и I

поля E и H не зависят от сре-

ды, заполняющей конденсатор и соленоид, соотношения (15.47) о стаются

справедливыми и в том случае, когда конденсатор и соленоид заполнены

веществом. Используя выражения (15.46) и (15.47), получаем следующие

формулы для средних по времени значений плотностей электрической и

магнитной энергий:

i =

8π

d(ωε)

dω

i (15.48)

i =

8π

d(ωµ)

dω

i. (15.49)

378

Как подчеркивается в [4], недостаток приведенного выше вывода со-

стоит в том, что дифференцирование функций ωL и ωC производится

вдоль мнимой оси, так как ˜ω − ω = iδ — величина чисто мнимая, а в

окончательных выражениях (15.48) и (15.49) производится подмена диф-

ференцированием по вещественной переменной ω. Так можно делать, ес-

ли функции ωL и ωC аналитические. В общей теории дисперсии, впро-

чем, аналитичность функций ε(ω) и µ(ω) док азывается.

Задача 15.4. Получить выражения для плотности электрической и маг-

нитной энергии на примере газа невзаимодействующих гармонических ос-

цилляторов — атомов, в каждом из ко торых всего один электрон, в элек-

трическом поле с частотой ω [5, гл. 3]. Вдали от собственной частоты ω

осциллятора затуханием можно пренебречь и для смещения r осциллятора

от положения равновесия пользоваться уравнением

+ ω

r =

E ,

где e и m — заряд и масса электрона.

Указание. В анализируемом случае энергия слагается из энергии самого

электрического поля (т. е. поля в вакууме) и из энергии частиц, находя-

щихся в поле (из кинетической и потенциальной энергии колеблющихся

осцилляторов). Следует также использовать формулу Зельмейера (см., на-

пример, гл. 3 в [5].

Задача 15.5. [4] Покажите, что, если ε(ω) и µ(ω) положительны, то фа-

зовая и групповая скорости в электромагнитной волне направлены в одну

сторону.

Общий способ вывода формулы для плотности энергииРассмотрим

теперь более общий способ вывода соотношений для плотности электро-

магнитного поля в среде с дисперсией.

Известное выражение S = (c/4π)[EH] для плотности потока электро-

магнитной энергии справедливо и в среде с дисперсией [6,7]. Из уравне-

ний Максвелла следует не менее известное уравнение

div S =

4π



∂D

∂t

+ H

∂B

∂t



. (15.50)

где E и D — напряженность и смещение электрического поля, H и B —

напряженность и индукция магнитного поля.

Если дисперсии нет, т. е. проницаемости ε и µ, — действительные по-

стоянные величины, то уравнение (15.50) выражает изменение плотности

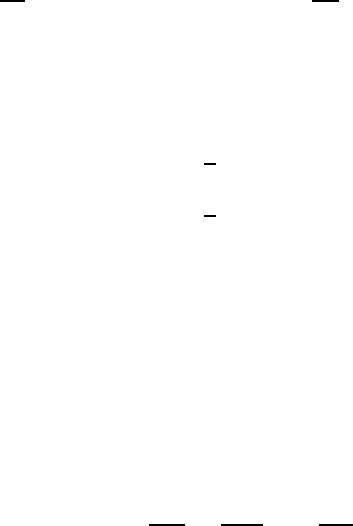
379

электромагнитной энергии E = (1/8π)(εE

+µH

) в единице объема, т. е.

dE/dt + div S = 0. При наличии диссипации плотность энергии тепловых

потерь определяется мнимыми частями ε и µ:

Q =

4π



Im εhE

i + Im µhH



∂E

∂t

+ div S + Q = 0 .

Найдем E, следуя [6]. Рассмотрим узкий волновой пакет, состоящий

из монохроматических компонент с частотами вблизи некоторой ω

, т. е.

узкий пакет с шириной спектра ∆ω  ω

E = E

(t)e

iω

Re E =



(t)e

iω

+ E

(t)e

−iω



H = H

(t)e

iω

Re H =



(t)e

iω

+ H

(t)e

−iω



(для D и B имеют место аналогичные выражения), где E

(t) и H

(t)

— медленно изменяющиеся по сравнению с exp(iω

t) функции време-

ни. Подставим выражение для действительных частей напряженностей

E, H, а также для D и B в (15.50) после чего усредним получившее-

ся по периоду 2π/ω

. Очевидно, что быстро меняющиеся слагаемые типа

(∂D

/∂t) exp(2iω

t) и E

(∂D

/∂t) exp(−2iω

t) при усреднении исчез-

нут, а о станутся лишь слагаемые типа

M =

16π



∂D

∂t

+ E

∂D

∂t



(мы делаем все преобразования только с первым слагаемым в правой

части (15.50)). Представим производную ∂D/∂t в виде

fE, где опера-

тор

f = (∂/∂t)ε. Что получится, если подействовать этим оператором

на E = E

exp iω

t? Очевидно, что если E

= const (поле чисто гармо-

ническое), то

fE = iω

ε(ω

)E или

fE = f (ω

)E, где f(ω) = iωε(ω).

Разложим функцию E

(t) в интеграл Фурье, что соответствует представ-

лению ее группой монохроматических составляющих E

0ω

exp[i(ω −ω

)t] с

0ω

= const:

(t) ∼

∞

−infty

0ω

i(ω−ω

d(ω − ω

) .

Поскольку E

(t) — медленно изменяющаяся функция времени, то в ин-

теграл войдут лишь те составляющие, для которых ∆ω = |ω − ω

|  ω

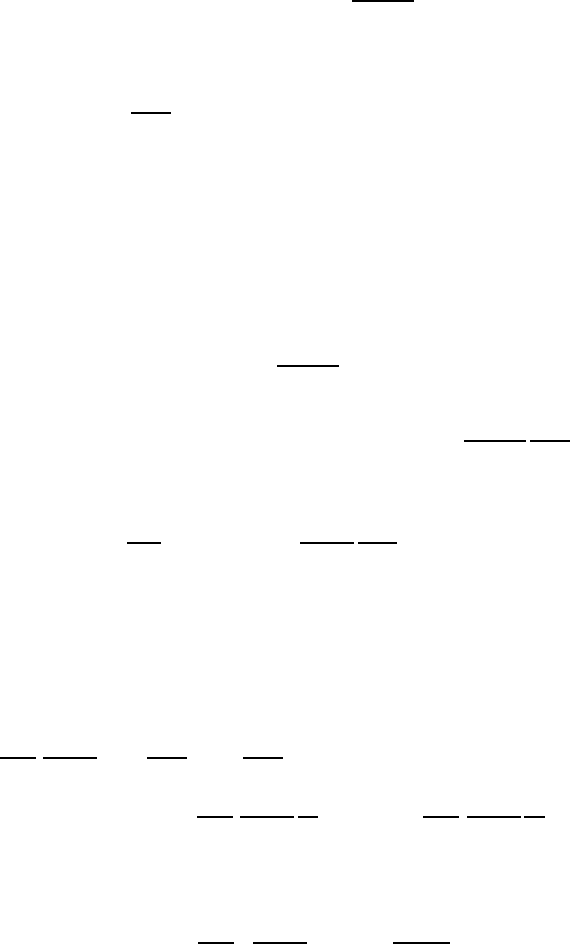
380

Это позволяет написать следующее соотношение:

0ω

i(ω

+∆ω)t

= f(ω

+ ∆ω)E

0ω

i(ω

+∆ω)t

≈

≈ f(ω

0ω

i(ω

+∆ω)t

+ ∆ω

df (ω

)

dω

0ω

i(ω

+∆ω)t

. (15.51)

Легко видеть, ч то

∂E

∂t

∼

∞

−∞

i∆ωE

0ω

i∆ωt

d(∆ω) . (15.52)

Проинтегрируем (15.51) по ∆ω в пределах от −∞ до ∞, что соответствует

обратному преобразованию Фурье. Используя (15.52), находим

iω

∞

−∞

0ω

i∆ωt

d(∆ω) =

= f(ω

iω

∞

−∞

0ω

i∆ωt

d(∆ω) − i

df (ω

)

dω

iω

∞

−∞

i∆ωE

0ω

i∆ωt

d(∆ω) =

= f(ω

iω

− i

df (ω

)

dω

∂E

∂t

iω

Опуская далее индекс 0 у ω

, получаем

∂D

∂t

= iωε(ω)E +

d(ωε)

dω

∂E

∂t

iωt

. (15.53)

Напомним, что ε(ω) = Re ε(ω) + i Im ε(ω) = ε

(ω) + iω

(ω). Те области

частот, в которых ε

(ω) малы по сравнению с ε

(ω), называются областя-

ми “прозрачности” среды (аналогично для магнитной проницаемости). В

этих областях можно положить ε

(ω) = 0, так что Q = 0. Учитывая, что

теперь ε(ω) = ε

(ω) = ε

(ω), имеем следующее соотношение для М:

M =

16π

d(ωε)

dω



∂E

∂t

+ E

∂E

∂t



16π

d(ωε)

dω

) =

16π

d(ωε)

dω

E) .

Поскольку для магнитного поля все выкладки аналогичны, можем напи-

сать выражение для усредненной плотности энергии

hE(t)i = hE

эл

i + hE

i =

16π



d(ωε)

dω

h|E|

i +

d(ωµ)

dω

h|H|



. (15.54)