Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны

Подождите немного. Документ загружается.

411

градиентом скорости dv

/dy = ω

/ω

= ω

, ω

и ω

— плазменная и

циклотронная частоты.

Для анализа высокочастотных волновых процессов в такой модели

предполагае тся, что все переменные изменяются во времени и в направле-

нии распространения волны (вдоль координаты x) по закону

exp[i(ωt−kx)]. Тогда для зависимой переменной F , связанной с y - компо-

нентой скорости формулой F (y) = (v

(y))

1 − s

(y), уравнение имеет

вид d

F/ds

− r

Q(s)F = 0, где Q(s) = 1 + 2r

/(s

− 1) + 3r

/(s

−

−1)

, s = −(ω −kv

(y))/ω

— аналог безразмерной координаты. Решение

этой задачи и нахождение поправок к приближению ВКБ обсуждаются,

например, в [4, 5].

В СВЧ электронике решения (17.10) используются также в теории рас-

пространения волн пространственного заряда в ускоренном электронном

потоке [6] и в двухволновой теории лампы обратной волны с медленно

изменяющейся вдоль направления движения электронов фазовой скоро-

стью электромагнитной волны [7]. (взаимодействуют только медленная

волна пространственного заряда и “синхронная” обратная пространствен-

ная гармоника замедляющей системы).

Вернемся к общему случаю трехмерной неоднородной среды и рассмо-

трим более подробно уравнение эйконала. Введем векторное поле p(r) с

помощью формулы

p(r) = ∇ψ . (17.12)

В каждой точке пространства вектор p перпендикулярен поверхности по-

стоянного значения эйконала (а значит и поверхности постоянной фазы),

а его длина p = |p|, согласно уравнению (17.7), равна p = n(r). Предполо-

жим сначала, что функция ψ(r) известна, тогда известно и векторное поле

p(r) во всем пространстве. Выберем произвольную т очку r

и проведем

через нее кривую, касательную в каждой точке к направлению вектора

p. Такая кривая называется лучом. Как следует из определения, луч в

каждой точку перпендикулярен поверхности постоянной фазы. Понятие

луча является центральным в геометрической оптике. Если построить се-

мейство лучей, покрывающее некоторую область пространства, то можно

получить решение уравнения эйконала. Покажем, как это сделать.

Прежде всего, получим дифференциальные уравнения для функции

r(s), задающей луч в параметрической форме. Здесь s — длина вдоль

луча от фиксированной точки r

до точки наблюдения r. Касательный к

лучу единичный вектор l согласно дифференциальной геометрии равен

dr/ds, и он по определению направлен вдоль вектора p. Поэтому можно

412

записать

= l . (17.13)

Рассмотрим функцию H(p, r) = [p

− n

(r)]/2. В соответствии с уравне-

нием (17.12), она принимает одно и тоже нулевое значение во всех точках

пространства, поэтому ее дифференциал равен нулю: dH = 0. Представим

это соотношение в виде

p · dp −

∇n

· dr = 0 ,

и поделим его на ds; кроме того, используем уравнение (17.13). В резуль-

тате получаем

p ·



−

∇n



= 0 ,

Это уравнение будет выполняться, если положить

∇n

. (17.14)

Учитывая, ч то p = n, и p = p l, приходим к дифференциальным уравне-

ниям для луча:

= l , (17.15a)

∇n

−



∇n

· l



l . (17.15b)

Для интегрирования уравнений (17.15) необходимо определить на-

чальные условия. Предположим, что известна гладкая поверхность по-

стоянной фазы волнового поля, на которой значение эйконала равно ψ

В этом случае для любой точки, принадлежащей поверхности, известно

направление нормального к ней вектора l

. Для л уча, проходящего через

эту точку, начальные условия выглядят следующим образом: r(0) = r

l(0) = ±l

. Разный выбор знаков соответствует двум волнам, распростра-

няющимся через точку r

в противоположные стороны. В более общем

случае в пространстве задана произвольная поверхность (не обязательно

с постоянной фазой), вдоль которой определена функция эйконала. Тогда

вектор ∇ψ не будет перпендикулярным поверхности и для восстановле-

ния нач альных условий необходимы дополнительные соображения. Мы

413

не будем о станавливаться на этом подробно, соответствующие формулы

можно найти, например, в [1].

После того, как форма луча найдена путем интегрирования уравнений

(17.15), можно найти закон изменения эйконала вдоль луча. Для этого

вычислим производную dψ/ds:

dψ

= ∇ψ ·

= p · l = n(r) .

Отсюда получаем

ψ = ψ

n(r) ds . (17.16)

Уравнениям для лучевой траектории можно придать другую форму,

которая делает их физически наглядными и допускающими простую ме-

ханическую интерпретацию. Вместо параметра s введем параметр τ с

помощью соотношения ds = p dτ. Тогда уравнения (17.13) и (17.14) при-

нимают вид

dτ

= p , (17.17a)

dτ

∇n

. (17.17b)

Их можно трактовать как уравнения движения частицы единичной мас-

сы в потенциальном поле U(r) = −n

(r)/2. Тогда введенная функция

H(r, p) = p

/2 + U(r) является функцией Гамильтона механической си-

стемы, а уравнения (17.17) сразу получаются как соответствующие урав-

нения Гамильтона [8]

dτ

∂H

∂p

dτ

= −

∂H

∂r

. (17.18)

Параметр τ выступает как время движения частицы по траектории, так

как масса частицы равна единице и справедлива формула τ =

−1

dτ.

Лучи совпадают с траекториями частиц, а для эйконала вдоль траектории

выполняется соотношение

ψ(τ) = ψ

(r) dτ . (17.19)

414

Подобная оптико-механическая аналогия дважды сыграла огромную

роль в развитии физики. Снач ала она была использована У.Гам ил ьтоном

для вывода уравнений механики в гамильтоновской формулировке, а за-

тем Шредингер применил эту же аналогию для получения кванто-механического

уравнения, носящего теперь его имя.

Уравнения лучей в форме (17.15) или (17.17) решают либо аналитиче-

ски, что возможно лишь в небольшом числе случаев, либо численно, что

при современном уровне развития численных методов не представляет

особых трудностей.

Обратимся теперь к уравнению переноса (17.8), определяющему за-

кон изменения амплитуды волны в пространстве. Используя соотношение

(17.12), запишем его в виде A

div p + 2p grad A

= 0, или

div(pA

) = 0 . (17.20)

Вектор I = pA

в нулевом приближении геометрической оптики про-

порционален вектору потока плотности энергии волны. Покажем это на

примере акустических волн. Плотность потока звуковой энергии равна

q = P

v [9], где P

— возмущение давления, v - скорость среды. Ис-

пользуя соотношения из главы 11 P

= −ρ

˙ϕ и v = ∇ϕ, получаем q = −

−ρ

˙ϕ ∇ϕ. Принимая во внимание гармоническую зависимость всех пере-

менных от времени, переходя от потенциала скоростей ϕ к его комплекс-

ной амплитуде u и усредняя выражение для q по периоду колебаний,

получаем

q = −

iωρ

(u∇u

− u

∇u) . (17.21)

В нулевом приближении u = A

exp(−ikψ). При дифференцирова-

нии этого выражения амплитудный множитель A

следует рассматривать

как постоянную величину, иначе будет получено превышение точности,

так как слагаемое, пропорциональное ∇A

, имеет тот же порядок, что и

слагаемое в дебаевском разложении, пропорциональное A

. Проводя вы-

числения с учетом этого правила, приходим к следующей формуле для

потока мощности акустической волны:

q =

ωkρ

∇ψA

ωkρ

Итак, уравнение переноса, записанное в форме (17.20), представляет со-

бой закон сохранения потока энергии.

415

Рис. 17.1. Лучевая трубка

Рассмотрим все лучи, проходящие через маленькую площадку dσ

перпендикулярную некоторой лучевой траектории (рис. 17.1). Такая сово-

купность лучей называется лучевой трубкой. Проинтегрируем уравнение

(17.20) по объему лучевой трубки. Используя теорему Гаусса, записываем

div I dV =

I · dS = 0 .

Интеграл по боковым поверхностям трубки обращается в нуль, а интеграл

по ее основаниям дает

dσ

= I dσ . (17.22)

Так как I = pA

= nA

, отсюда получаем формулу для амплитуды A

(r):

(r) = A

)

n(r

)

n(r)

dσ

, (17.23)

где A

) — значение амплитуды, заданное на исходной поверхности.

Таким образом, интегрирование уравнений (17.15) или (17.17) позволяет

построить семейство лучей, а использование формул (17.16) и (17.23) —

найти распределение амплитуды и фазы поля вдоль каждого луча.

§ 2. Образование каустик и рефрация

Картина распространения возмущений вдоль лучей, задаваемая гео-

метрической оптикой, оказывается существенно более богатой, чем это

кажется на первый взгляд, благодаря образованию каустик, являющих-

ся огибающими семейств лучевых траекторий.

416

Рис. 17.2. Образование каустики в однородной среде вбли-

зи вогнутого участка волнового фронта (а) и поведение

лучей вблизи каустики (б).

Существует две причины появления каустик. Первая имеет чисто гео-

метрическую природу. Предположим, что начальный волновой фронт име-

ет вогнутый участок, как это показано на рис. 17.2,а, а среда однородная.

Тогда лучи являются отрезками прямых и непосредственное построение

показывает, что вблизи вогнутого участка волнового фронта образуется

область, через каждую точку которой проходят три луча. Граница обла-

сти является огибающей семейства лучей — это и есть каустика. На рис.

17.2,б в увеличенном масштабе показан участок каустики и поведение

лучей вблизи него. Из рисунка видно, что в точке касания сечение луче-

вой трубки обращается в нуль и в соответствии с формулой (17.23) это

означает, чт о на каустике амплитуда поля стремится к бесконечности.

На самом деле в точном решении уравнения (17.1) бесконечности по-

явиться не может. Прот иворечие объясняется тем, что вблизи каустики

нарушается условие применимости геометрической оптики, и в этой обла-

сти необходимо учитывать дифракционные явления, описывающие про-

сачивание поля за каустику [1, 10]

Хотя близи каустики решение в форме u = A

exp(−ikψ) оказывается

неприменимым, после ее прохождения им снова можно пользоваться. При

этом, однако , следует учитывать так называемое “правило сдвига фазы”,

состоящее в том, что после касания каустики поле вдоль луча приобретает

дополнительный сдвиг фазы, равный −π/2. Полное выражение для поля

с учетом этого правила имеет вид

u(r) = A

)

n(r

)

n(r)



dσ



exp(−ikψ − iπm/2) , (17.24)

417

Рис. 17.3. Изменение ориентации сечения лучевой трубки

при касании каустики

где m — число касания каустик при прохождении луча от точки r

до

точки набл юдения r. Происхождение фазового сдвига связано с эффек-

тами дифракции и его величина может быть найдена при анализе точно-

го решения волнового уравнения вблизи каустики. Для случая слоисто-

неоднородной среды это будет сделано в параграфе § 4. Качественно про-

исхождение фазового множителя можно понять, обратившись к рис. 17.3.

Из него видно, что после касания каустики элемент dσ сечения луче-

вой трубки меняет ориентацию, поэтому вместо соотношения (17.22) фор-

мально следует записать I

dσ

= −I dσ. При извлечении корня из этого

соотношения в формуле (17.23) появляется дополнительный множитель

exp(−iπ/2) перед амплитудой.

Если среда неоднородная, каустика может появиться и в случае плос-

кого ил и выпуклого начального фронта волны. Рассмотрим в качестве

важного примера слоисто-неоднородную среду, в которой показатель пре-

ломления зависит только от одной из координат, например от z, т.е. по-

ложим n = n(z). Лучи в этом случае целиком лежат в одной плоскости,

которую выберем в качестве плоскости xz. Форму лучей получим, ис-

пользуя второе из уравнений (17.17). Расписанное по координатам, оно

приводит к соотношениям

dτ

= 0 ,

dτ

= n(z)n

(z) . (17.25)

Интегрируя первое уравнение, имеем

= n(z) cos θ(z) = n(0) cos θ

= const , (17.26)

где n(z) и θ(z) — значение показателя преломления и угол наклона луча

к оси x в точке c вертикальной координатой z. Уравнение (17.26) яв-

ляется обобщением закона Снеллиуса для слоисто-неоднородной среды.

418

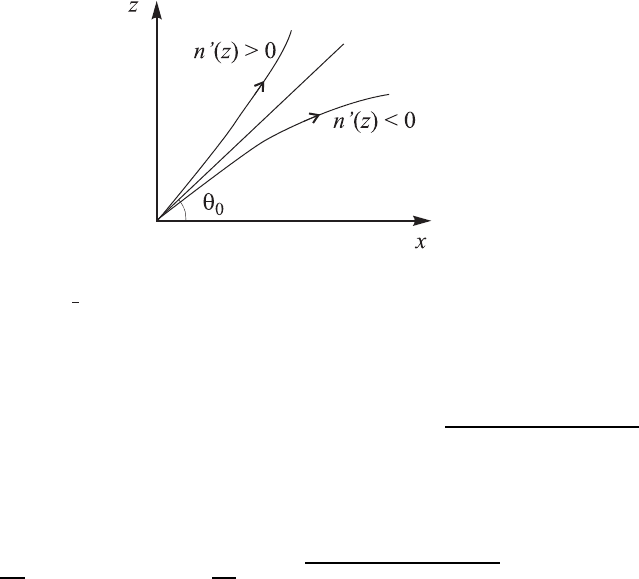
Рис. 17.4. Искривление луча в слоисто-неоднородной среде.

При своем распространении, луч поворачивается таким образом, чтобы

величина n(z) cos θ(z) оставалась постоянной.

Вместо интегрирования второго уравнения в (17.25), воспользуемся

соотношением p

+ p

= n

(z), т огда p

(z) = ±

(z) − n

(0) cos

Знак плюс соответствует восходящему, а знак минус — нисходящему

участку луча. Используя эти выражения в первом уравнении системы

(17.17), расписанном по координатам, получаем

dτ

= n(0) cos θ

dτ

= ±

(z) − n

(0) cos

. (17.27)

Легко видеть, ч то уравнения (17.25) и (17.27) идентичны уравнениям дви-

жения частицы единичной массы, брошенной под углом θ

к горизонту

c начальной скоростью n(0) в вертикально направленном потенциальном

поле U(z) = −n

(z)/2. Исходя из этой механической аналогии сразу

можно утверждать, что если показатель преломления увеличивается с

высотой, то луч изгибается вверх и, напротив, если показатель прелом-

ления уменьшается с высотой, луч изгибае тся вниз, как это показано

на рис. 17.4. В любом случае луч поворачивается в сторону увеличения

показателя преломления.

Предположим, что n

(z) < 0 для всех z > 0 и уравнение n(z) =

= n(0) cos θ

имеет действительный корень z

. Тогда из формулы (17.26)

следует, что в плоскости z = z

угол наклона луча равен нулю, т о есть

он параллелен оси x. После прохождения этой точки начинается нис-

ходящий участок луча. Плоскость z = z

, которой касаются все лучи,

имеющие одинаковый наклон θ

в начальной плоскости, является к аусти-

кой (см. рис. 17.5,а). В неоднородной среде каустика может образовать-

ся и в том случае, если начальный волновой фронт является выпуклым

419

Рис. 17.5. Образование каустики в плоско-слоистой среде

в случае плоского (а) и выпуклого (б) начального фронта

волны.

(рис. 17.5,б).

Искривление лучей из-за неоднородности среды носит название ре-

фракции. Явление рефракции играет большую роль при распростране-

нии радиоволн, акустических волн в океане, волн в плазме и во многих

других приложениях. Приведем несколько примеров.

Рассмотрим распространение звуковых волн в атмосфере при наличии

градиента температуры [11]. Пусть температура воздуха меняется с высо-

той по закону T (z). Тогда скорость звука c(z) меняется в соответствии с

формулой

c(z) =

γRT (z) ,

где R — газовая постоянная, γ = c

. Показатель преломления в зави-

симости от высоты равен n(z) = c

/c =

/T . По закону Снеллиуса

cos θ = cos θ

. (17.28)

Если, как это обычно бывает при нормальных условиях, температура

уменьшается с высотой, т.е. T

(z) < 0, угол наклона звукового луча к

горизонтали увеличивается — он отклоняется вверх. Иногда может воз-

никнуть противоположная ситуация, когда температура увеличивается с

высотой. Такое наблюдается, например, вечером в тихую погоду над по-

верхностью реки. В этом случае звуковые лучи отклоняются вниз, обес-

печивая усиление волны в горизонтальном направлении. Именно рефрак-

цией объясняется тот факт, что вечером даже тихий разговор в лодке

можно услышать на большом расстоянии.

420

Рис. 17.6. К определению радиуса кривизны луча в неод-

нородной среде.

В качестве второго примера упомянем тропосферную рефракцию,

которая возникает при распространении ультракоротких волн в тропо-

сфере Земли [12]. Тропосфера — это нижняя часть атмосферы Земли,

она простирается до высот 10–12 километров и вмещает в себя примерно

80 % массы воздуха. Диэлектрическ ая проницаемость воздуха атмосфе-

ры очень близка к единице. Вблизи земной поверхности в среднем n −

− 1 ≈ 3,25·10

−4

и с увеличением высоты она постепенно уменьшается со

средней скоростью dn/dz ≈ −4·10

−5

км

−1

Несмотря на столь малые отклонения показателя преломления от еди-

ницы, рефракция в тропосфере оказывается заметной благодаря тому,

что радиус кривизны радиолуча сравним с радиусом Земли. Рассмотрим

участок луча, показанный на рис. 17.6. Радиус кривизны можно опре-

делить, используя формулу (17.15b). Прежде всего отметим, что вектор

dl/ds перпендикулярен вектору l, так как l · l = 1. Из (17.15b) следует,

что векторы ∇n/n, l и dl/ds принадлежат одной плоскости, также, как

и вписанная в точке A в траекторию л уча окружность, радиус которой

равен R. При смещении точки наблюдения из A в B, параметр s уве-

личивается на dS = Rα, а конец вектора l перемещается на величину

∆l = |l|α = α. Поэтому |dl/α| = R

−1

. Используя формулу векторного

анализа [A, [B, C]] = B(A · C) − C(A · B), уравнение (17.15b) можно

представить в виде



∇n

, l



. (17.29)