Troyan V., Kiselev Y. Statistical Methods of Geophysical Data Processing
Подождите немного. Документ загружается.


Basic concepts of the probability theory 53
are the sample expectation and sample variance accordingly, have the Student’s
distribution with n − 1 degrees of freedom. The density function for the Student’s
distribution is given by the formula (Fig. 1.34):
f
η
(t) =
Γ((n + 1)/2)
√
nπΓ(n/2)
1 +
t
2
n
−(n+1)/2
. (1.47)
Fig. 1.34 Student’s distribution: 1 — n = 1; 2 — n = 10.
• Mathematical expectation: Mη = 0.
• Variance: Dη = n/(n − 2), n > 2.
• Asymmetry coefficient: γ
1
= 0.
• Excess: γ
2
= 6/(n − 4), n > 4.
At the numerator of η (from (1.46)) is placed the random variable
η
1
=
√
n(
¯
ξ − m
ξ
),
which has the normal distribution N(0, σ
2
). A random variable η
2
, which is the
sample variance, is placed at the denominator of (1.46) and, as mentioned above,
η
2
is independent from random variable η
1
. The random variable (n − 1)s
2
/σ
2
has
the χ
2
-distribution with (n − 1) degrees of freedom.
The Student’s distribution is symmetric relatively of t = 0. If n = 1 then
the Student’s distribution transforms to the Cauchy distribution and at n → ∞ it
tends to the standard normal distribution N(0, 1). Using the Student’s distribution
function is possible to draw the confidence interval for the mathematical expectation
m
ξ
.
1.8.6 Fisher distribution and Z-distribution
Let us ξ
1
, ξ
2
, . . . , ξ
n
1
and η
1
, η
2
, . . . , η
n
2
are the random variables which belong to
normal distribution ξ
i
∈ N(m
1
, σ
2
1
) and η
i
∈ N(m
2
, σ
2
2
) accordingly. Their sample
variances
s
2
1
=
1
n
1
− 1
n
1
X
i=1
(ξ
i
−
¯
ξ)
2
and s
2
2
=
1
n
2
− 1
n
2
X
i=1
(η
i
− ¯η)
2

54 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING
are independent and the random values n
1
s
2
1
/σ
2
1
and n
2
s
2
2
/σ
2
2
have the distributions
χ
2
n
1
and χ
2
n
2
accordingly. It is said, that random variable
ζ =
s
2
1
σ
2
1
σ
2
2
s
2
2
(1.48)
has the Fisher distribution or F -distribution (or distribution of ratio of variances)
with (n
1
, n
2
) degrees of freedom (Fig. 1.35):
f
ζ
(F ) =
n
n
2
/2
1
n
n
1
/2
2
F (
n
1
+n
2
2
)
Γ(
n
1
2
)Γ(
n
2
2
)
F
(n
1
/2)−1
(n
1
+ n
2
F )
(n
1
+n
2
)/2
,
where degrees of freedom n
1
and n
2
are the parameters of distribution.
Fig. 1.35 Fisher distribution (n
1
= 5, n
2
= 50).
• Mathematical expectation: Mζ = n
2
/n
2
− 2, n
2
> 2.
• Variance:
Dζ =
2n
2
2
(n
1
+ n
2
− 2)
n
1
(n
2
− 2)
2
(n
2
− 4)
, n
2
> 4.
The Fisher distribution is positive and asymmetric one and tends to the normal
distribution for n
1
, n
2
→ ∞, but rather slowly. If (n
1
, n
2
> 50) then the Fisher
distribution is close to the normal distribution. The Fisher distribution is used
in tasks of a test of hypothesis, for example, at the definition of a degree of an
polynomial approximation.
The random variable Z = (1/2) ln F (Z is a real number) has a distribution which
is considerably close to the normal one and the distribution is called Z-distribution.
The parameters of Z-distribution are the degrees of freedom n
1
and n
2
. The density
function reads as
f(Z) =
2n
n
1
/2
1
n
n
2
/2
2
B(n
1
/2, n
2
/2)
e
n
1
z
[n
1
e
2z
+ n
2
]
(n
1
+n
2
)/2
,
The mathematical expectation and variance are given accordingly by the formulae
Mζ =
1
2
[n
−1
2
− n
−1
1
] −
1
6
[n
−2
1
− n
−2
2
]
and
Dζ =
1
2
[n
−1
1
+ n
−1
2
] +
1
2
[n
−2
1
+ n
−2
2
] +
1
3
[n
−3
1
+ n
−3
2
].
Z-distribution is used for an estimation of the confidence interval for the correlation
coefficient.

Basic concepts of the probability theory 55
1.8.7 Triangular distribution
The random variable ξ has the triangular distribution, if its distribution function
describes by formula
f
ξ
(x) =
r
−1
+ |x − m|/r
2
, if m − r < x < m + r,
0, for all others x.
The parameters of distribution: m, r > 0.
• Mathematical expectation: m
ξ
= m.
• Variance: Dξ = r
2
/6.
• Asymmetry coefficient: γ
1
− 0.
• Excess γ
2
= −0.6.
As an example of appearance of the triangular distribution it is possible to
consider a sum of two independent random variables ξ
1
and ξ
2
, which have the
uniform distribution.
1.8.8 Beta distribution
The random variable ξ has the beta distribution, if its density function can be
represented as
f
ξ
(x) =
(
Γ(n+m)
Γ(n)Γ(m)
x
m−1
(1 − x)
n−1
, if 0 < x < 1,
0, for all others x,
where n and m are positive integers.
• Mathematical expectation: Mξ = m/(m + n).
• Variance:
Dξ =
mn
(m + n)
2
(m + n + 1)
.
The beta distribution is used in the mathematical statistics, when the random
variables with double limiting, for example 0 < x < 1, are considered.
1.8.9 Exponential distribution
The random variable ξ has the exponential distribution, if its density function can
be represented as
f
ξ
(x) =
λ exp(−λx), if x ≥ 0,
0, if x < 0,
(1.49)
where λ > 0 is a positive number (the parameter of distribution) (Fig. 1.36).
• Mathematical expectation: Mξ = λ
−1
.
• Variance: Dξ = λ
−2
.
• Asymmetry coefficient: γ
1
= 2.

56 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING
Fig. 1.36 Exponential distribution: 1 — λ = 2, 2 — λ = 4.
• Excess: γ
2
= 6.
The characteristic function is given by the formula
g(t) = (1 − it/λ)
−1
.
The exponential distribution has significance in the theory of Markovian pro-
cesses. If on the time axis there is a stationary Poisson flow with the intensity λ,
the interval of time between two adjacent events has an exponential distribution
with the parameter λ.
1.8.10 Laplace distribution
The random variable ξ has the Laplace distribution, if its density function can be
written as
f
ξ
(x) = (λ/2) exp(−λ|x|), (1.50)
where λ is a parameter of the distribution (Fig. 1.37).
Fig. 1.37 Laplace distribution: 1 — λ = 2, 2 — λ = 4.
• Mathematical expectation: Mξ = 0.
• Variance: Dξ = 2/λ
2
.
The Laplace distribution plays a vital part at the robust estimation, when the
models with a great spread of data are considered.

Basic concepts of the probability theory 57
1.8.11 Cauchy distribution
The random variable ζ with the density function
f
ζ
(x) = (1/π)(1/(1 + x
2
)) (1.51)
has the Cauchy distribution (Fig. 1.38). This distribution can be obtained as a
Fig. 1.38 Cauchy distribution.
distribution of a ratio ζ = ξ/η of two random variables with standard normal
distributions: ξ ∈ N (0, 1), η ∈ N(0, 1).
The mathematical expectation Mζ is undefined and variance, asymmetry coeffi-
cient, excess are represented by the divergent integrals. The characteristic function
is written as
g(t) = exp(−|t|).
The Cauchy distribution has the special place in the probability theory and
applications – its mathematical expectation is undefined and all other moments are
divergent.
1.8.12 Logarithmic normal distribution
If the random variable η = ln ξ has the normal distribution, then the density func-
tion f
ξ
(x) is called logarithmic normal and is written as (Fig. 1.39):
f
ξ
(x) =
1
√
2πσx
exp
−1
2σ
2
(ln x − m)
2
, (1.52)
where m, σ are the distribution parameters.
Fig. 1.39 Logarithmic normal distribution. (a) — m = 2.0, σ = 0.5 (1); 1.0 (2); 1.5 (3); (b) —
σ = 1.0, m = 1.0 (1); 1.5 (2); 2.0 (3).
58 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING
• Mathematical expectation: Mξ = exp(m − σ
2
/2).
• Variance: Dξ = exp(2m + σ
2
)(exp(σ
2
) − 1).
• Asymmetry coefficient: γ
1
= (exp(σ
2
) − 1)
1/2
(exp(σ
2
) + 2).
• Excess:
γ
2
= (exp(σ
2
) − 1)(exp(3σ
2
) + 3 exp(2σ
2
) + 6 exp(σ
2
) + 6).
The logarithmic normal distribution is used as a model for the description of
errors of a random process, which include a great number of multiplicative errors.
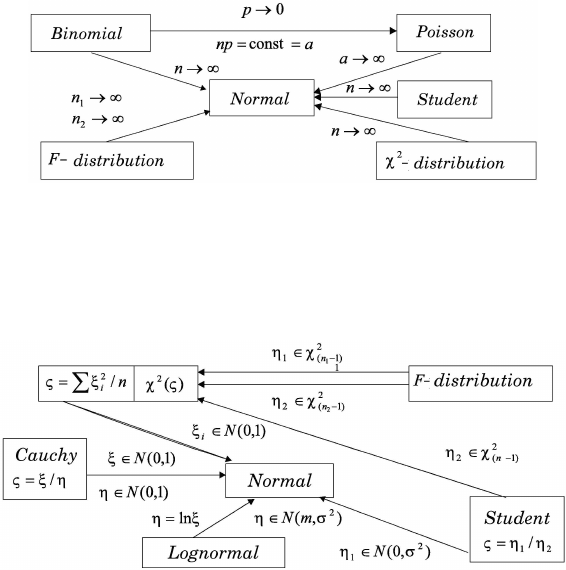
1.8.13 Significance of the normal distribution
The mentioned above distributions, which using more frequently for the description
of the geophysical models, are connected with the normal distribution. The most
part of these distributions either asymptotically tend to the normal distribution
or appearance of them is induced by the normal distribution. The asymptotic
properties of the distributions and their connection with the normal distribution
are represented at Fig. 1.40.
Fig. 1.40 The asymptotic properties of the distributions and their connection with the normal
distribution.
The probability distributions of random variables being the functions of random
variables with the normal distribution, are represented in Fig. 1.41.
Fig. 1.41 Probability distributions, defined on the basis of the normal distribution.

Basic concepts of the probability theory 59
1.8.14 Confidence intervals
Owing to a randomness of outcomes of the random experiment it is impossible
to establish narrow limits for possible deviations of an estimate of the parameter
from its true value. Therefore there is a problem of a definition by the results of
experiments of such limits, which the error of the estimation would not go out with
a given probability.
The random interval, which covers the unknown parameter ρ with the given
probability β
P (|˜ρ − ρ| < ε) = β, P (˜ρ − ε < ρ < ˜ρ + ε) = β,
is called the confidence interval for the given parameters, and the probability β is
called the confidence probability. The quantity 1 −β is called the significance level.
The endpoints of the confidence interval I
β
= (˜ρ − ε, ˜ρ + ε) are determined by the
confidence bounds.
Let us consider the creation of the confidence interval for the mathematical
expectation and variance. It should be noted, that the problem of determination
of such confidence intervals for an arbitrary number of the experiments n is solved
for the case of the normal distribution of the random variable ξ. At creation of the
confidence interval we shall use a sample estimate for the mathematical expectation
˜ρ:
˜ρ =
¯
ξ =
1
n
n
X
i=1
ξ
i
,
which is the arithmetic mean of the quantities ξ
i
, which obtained from n independent
experiments.
If the variance σ
2
ξ
of the random value ξ is known, the sample mean
¯
ξ has
the normal distribution with the mathematical expectation m
ξ
and the standard
deviation σ
m
= σ
ξ
/
√
n, therefore
P {−l ≤ (
¯
ξ − m
ξ
)
√
n/σ
ξ
≤ l} = 2Φ(l) − 1,
P {
¯
ξ − lσ
ξ
/
√
n ≤ m
ξ
≤
¯
ξ + lσ
ξ
/
√
n} = 2Φ(l) − 1.
If the variance σ
2
ξ
is unknown, let us consider the random value
η =
√
n(
¯
ξ − m
ξ
)/s,
where
s
2
=
1
n − 1
n
X
i=1
(ξ
i
−
¯
ξ)
2
(1.53)
is the sample variance of random variable ξ. It is possible to prove, that the random
variable η has the Student’s distribution and it leads to the determination of the
confidence interval, P {|η| < t
β
} = β:
P {
¯
ξ − t
β
s/
√
n ≤ m
ξ
≤
¯
ξ + t
β
s/
√
n} = β.
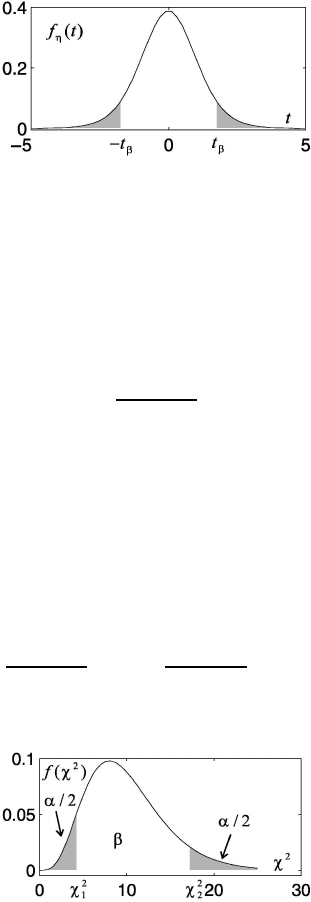
60 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING
Fig. 1.42 Student’s distribution (n=10) and the confidence interval (β = 0.95).
At Fig. 1.42 the confidence interval for the Student’s distribution is represented by
the confidence probability β = 0.95.
To find the confidence interval for the variance σ
2
ξ
of random variable ξ (ξ
i
∈
N(m
ξ
, σ
2
ξ
)). The quantities ξ
1
, ξ
2
, . . . , ξ
n
are obtained as the results of n indepen-
dent experiments. It is possible to prove, that the random value
(n − 1)s
2
σ
2
ξ
has χ
2
–distribution with n −1 degrees of freedom. To take into account the follow
equalities
1 − P (χ
2
> χ
2
1
) = P (χ
2
< χ
2
1
) = α/2, P (χ
2
> χ
2
2
) = α/2,
P (χ
2
1
< (n − 1)s
2
/σ
2
< χ
2
2
) = 1 − P (χ
2
< χ
2
1
) − P (χ
2
> χ
2
2
) = 1 − α,
let to write an expression, which connects the length of the confidence interval with
the significance level α:
P
(n − 1)s
2
χ
2
2
< σ
2
<
(n − 1)s
2
χ
2
1
= 1 − α.
At Fig. 1.43 the areas with the significance level of α=0.13 are marked.
Fig. 1.43 χ
2
–distribution: α=0.13.
1.8.15 Exercises
(1) To find the distribution function F
ξ
(x) for the random variable ξ, which has
the uniform density function on the interval (a, b).
Basic concepts of the probability theory 61
(2) The random variable has the Simpson’s distribution (triangular distribution)
on the interval (−a, a). To draw the distribution function graph. To calculate
Mξ, Dξ, γ
1
. To find the probability of hitting of the random variable ξ into
the interval (a/2, a).
(3) The quality control of detonators for an explosive source on seismic survey
is implemented in the following way. If a resistance R of the detonator is
satisfied the inequalities R
1
< R < R
2
, then the detonator can be used, but
if the inequalities are not valid, then the detonator rejects as defective. It is
known, that the resistance of the detonator has the normal distribution with
the mathematical expectation MR = (R
1
+R
2
)/2 and standard deviation σ
R
=
(R
2
− R
1
)/4. To find the probability of the rejecting of the detonator.
(4) For the case of the above considered task, to find the standard deviation of
the resistance of the detonator σ
R
, if it is known, that rejection is 10 % of all
detonators.
(5) During a device operation at the random moments can be malfunctions. The
time T of the device operation up to the first malfunction is distributed under
the exponential law f
ξ
(t) = ν exp{−νt} with parameter ν (t > 0). The mal-
function is immediately discovered and the device acts in repair. The duration
of repair is equal t
0
, then the device again acts in operation. To find the den-
sity function f
ζ
(t) and cumulative distribution function F
ζ
(t) of a time interval
ζ between two neighboring defects. To find its mathematical expectation and
variance. To find probability that ζ will be greater than 2t
0
.
(6) Consider the Poisson field of points with the constant density λ. To find a
distribution law and the numerical characteristics m
r
, D
r
for a distance apart
arbitrary point and a nearest neighbor point.
(7) In the some star set the stars are three-dimensional Poisson field of points with
the density λ (the mathematical expectation of a number of stars per unit
volume). Let us to fix one (arbitrary) star and to consider the nearest star,
the next (second) star with greater distance, third star and so on. To find the
distribution low for the distance between the fixed star and the n-the star in
this line.
(8) The iron-manganese concretions are placed at the bottom of ocean in the ran-
dom points and forms the Poisson field of points with a density λ (mathematical
expectation of number of concretions per unit area). The arbitrary point O at
the bottom is chosen. Consider the random variable R
1
, which is a distance
between the point O and the nearest concretion. To find the distribution of R
1
.
(9) Let us consider an amplitude of seismic signal at the time point t
0
as a random
variable ξ which has the normal distribution and the mathematical expectation
m
ξ
= 0. There is an interval (α, β) and origin of coordinates does not belong to
this interval. At what value of the standard deviation the probability of hitting
the random variable ξ inside the interval (α, β) will be maximum?

62 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING
1.9 Information and Entropy
A physical matter of the information appears from thermodynamics and statistical
physics and is based on a notion of entropy, which is a measure of the state of
indeterminacy of the physical system.
1.9.1 Entropy of the set of discrete states of system
In a case of a finite set of the possible states of a system x
1
, x
2
, . . . , x
n
(with
probabilities p
1
, p
2
,. . . , p
n
,), which forms a complete group of the disjoint events,
the entropy is defined by the formula
H = −
n
X
i=1
p
i
log p
i
. (1.54)
A choice of the base of the logarithm is determined a unit of the entropy If the base
of logarithm is 2, then we deal with binary unit of information bit.
1
, If the bases of
logarithm are e or 10 we deal with Napierian or Hartley units correspondingly. If
we choose 2 as the base of logarithm, then unit value of entropy corresponds to a
simplest system of two equally possible states
x x
1
x
2
p 1/2 1/2
,
and
H = −
1
2
log
1
2
+
1
2
log
1
2
= 1
this is the entropy of the bit site if it can be 0 or 1 with the equal probability.
If the system has n equiprobable states x
i
with probabilities p
i
= 1/n, then the
entropy of the system is equal
H = −n
1
n
log
1
n
= log n.
If we know the state of the system a priori, then its entropy is equal to H = 0.
In this case all states have the probabilities p
i
= 0, except for one state p
i
0
= 1.
The entropy of a system with a finite set of states reaches a maximum, when all
states are equiprobable.
The entropy can be represented as the mathematical expectation
H
ξ
= M[−log p
ξ
], (1.55)
where log p
ξ
is a logarithm of the probability of the random state of the system,
which is considered as the random variable ξ.
1
A word bit is made up the words binary digit.
