Troyan V., Kiselev Y. Statistical Methods of Geophysical Data Processing

Подождите немного. Документ загружается.

Chapter 2

Elements of mathematical statistics

The mathematical statistics studies both statistical description of experimental

observations, and checkout of competing mathematical models describing natural

physical process. The mathematical statistics is the basic tool of processing of re-

sults of physical, including geophysical, experiments with the minimum losses of the

information about investigated object.

The basic notion of the mathematical statistics is the sample or block of ob-

servations ξ = (x

, x

, . . . , x

) of any quantitative variable. If this variable is a

random one, the sample

ξ = (x

, x

, . . . , x

) is a random vector. The number n is

called as the sample size. The sample is called repeated, if the components of the

vector ξ are independent and identically distributed. Any function g(x

, x

, . . . , x

)

of observations (x

, x

, . . . , x

) is called the statistics.

The examples of the statistics:

• sample mean ¯x = (1/n)

i=1

;

• sample variance s

= (1/n)

i=1

− ¯x)

;

• sample variance coeﬃcient v = s/¯x;

• greatest sample element x

max

;

• least sample element x

min

The modern level of a geophysical experiment is characterized by the great data

ﬂow. So, at realization of seismic operations by the sea for one day 10

bit of the

information is ﬁled. Thus the visualization of the data, even without interpretation,

is impossible without application of statistical methods of processing of the seismic

data.

2.1 The Basic Concepts of the Decision Theory

The results (measurement data) of a real geophysical experiment are always random

because of an inevitable presence of errors of measuring. These data represent val-

ues of a random vector ξ with the distribution f(xx, θ) which is considered partially

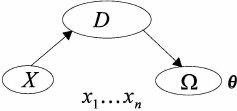
84 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

known. It is supposed, that parameter θ is an element of a set Ω (space of param-

eters). The observations ξ

ξ usually are used for deriving the information about the

distribution of

ξ or about a value of the parameter θ (vector of parameters θ

θ), on

which it depends. The implementation of the statistical analysis is necessary in con-

nection with the indeterminacy of an interpretation of results of observations, arising

because of the ignorance of the distribution of

ξ and consequently the ignorance of

basic elements of the mathematical model of a phenomenon. Therefore there is an

indeterminacy in a choice of best “activities” according to results of observations.

The problem is to ﬁnd a rule erecting correspondence between results of observa-

tions and reached decision. This correspondence is given by the decision function

δ(x

, . . . , x

) (decision rule), which to each sample of experimental data x

, . . . , x

assigns a particular expedient of an activity or a decision d = δ(x

, . . . , x

), and

the domain of the deﬁnition of this function is the set X, and a range of values

is the set of the possible decisions D. In the decision theory for a choice of the

function δ the loss function ϕ(θ, d) is introduced, which describes the losses, bound

with a decision making d provided that the distribution of ξ is equal f(xx, θ) and θ

is considered as a true parameter.

It is possible to emphasize the following basic elements, which deﬁne a solution

of problems of the mathematical statistician.

(1) Distribution class F = {f (

θ), θθ ∈ Ω}, in which distribution of ξ is included.

(2) Structure of the space D of possible decisions d, d ∈ D.

(3) The shapes of a loss function ϕ(θ, d).

In this connection three various spaces are used. The observation space X con-

tains all possible results of observations. The parameter space Ω contains all possible

values of the parameter θ or vector of parameters θ = (θ

, . . . , θ

). The decision

space D contains all possible decisions. The connections between spaces X, D and

Ω are shown at Fig. 2.1.

Fig. 2.1 The connection between spaces X, D and Ω.

The loss function ϕ(θ, d) is a random value, because d = δ(ξξ) depends on a

random vector ξ. It is possible to deﬁne an average loss, which arises from the

application of the decision rule d = δ(ξξ) at major number of repeated observations in

an experiment, approximately as the mathematical expectation of the loss function:

(θ) = M [ϕ(θ, δ(

ξ))] =

. . .

ϕ(θ, δ(ξ))f

(x, θ)dx

. . . dx

Elements of mathematical statistics 85

The function R

(θ) is called the risk function for the decision rule δ.

If we consider θ as a random variable and there is a priori density function f(θ),

then the notion of Bayes risk is introduced:

f(θ)

(δ) =

(θ)f (θ)dθ,

f(θ)

(δ) = M

[ϕ(θ, δ(

ξ))]] .

Let us consider the main elements, which deﬁne the statistical problem deﬁni-

tion.

2.1.1 Distribution class of the statistical problem

Deﬁnition of the distribution class f(x, θ) is based on a priori information about

properties of the random observations and an experiment environment.

Example 2.1. If in a ﬁxed time or spatial interval the probability of an occurrence

more than one event (seismic wave) in a small time interval is quantity of higher

order of smallness, than probability of the occurrence of one event (seismic wave),

and if such events are nonoverlapping intervals statistically independent, at these

guesses the number of occurrence of events (seismic waves) is described by the

Poisson distribution:

P (ξ = m) =

−a

(m = 1, 2 . . . ).

Example 2.2. The study of a microseism shows, that they are a sum of a great

number of the independent factors, and the inﬂuence of each of them it is very

small in comparison with all total, hence, at the realization of conditions of the

central limit theorem it is possible to make the guess about a normal distribution

of microseism ξ ∈ N(m

, D

Usually type of distribution is chosen from the preliminary analysis of the ex-

periment statement and the physical nature of investigated ﬁelds and errors of

measurements. The vector of parameters θ is determined during the solution of a

problem.

2.1.2 The structure of the decision space and the loss function

The structure of a decision space substantially determines a type of a current sta-

tistical problem, i.e. it underlies an expedient of the classiﬁcation of statistical

problems.

Example 2.3. Let us (x

, x

, . . . , x

) is a sample belonging to a sample population

with the distribution f (x, θ), where θ is an unknown parameter of the distribution,

as, for example, in the cases of the considered earlier Poisson distribution (θ = a)

86 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

and the Gaussian distribution

θ = (m

, D

), and let us γ = γ(θ) is a real function

of the parameter.

(A) If it is necessary to determine, exceeds γ(θ) some threshold value γ

whether

or not, then pick one from the solutions: d

: γ > γ

or d

: γ ≤ γ

. The

loss function ϕ(γ, d) is picked usually so that it is equal to zero, if the right

decision is chosen, and it is a steadily increasing function |γ−γ

| at the incorrect

decision. Such statement agrees with a task of a single signal extraction (on a

noise background). In this case γ is a relation) signal/noise, γ

is the threshold

relation signal/noise, d

is a presence of the signal, d

is an absence of the

signal.

(B) If it is necessary to ﬁnd numerical value of γ(θ), then in this case, the decision

d is equal to an estimate of ˆγ(θ). The loss function is usually represented

as ϕ(γ, d) = w(γ)ψ(|d − γ|), where ψ(|d − γ|) is the steadily increasing error

function |ˆγ −γ|, relevant to a deviation of an estimate from a true value. More

often in the estimation theory the square-law loss function is used. So, for

γ(θ) = θ, d =

θ we shall obtain

ϕ(θθ −

θ) = (θ −

θ)

W (θθ −

θ)

for the vector parameter and

ϕ(θ −

θ) = w(θ −

θ)

for the scalar parameter θ.

be considered as an example of the point estimation problem: u

= Aϕ(t

−τ)

+ ε

with the vector parameter θ

θ = (A, τ ).

(D) If at decision-making it is necessary to estimate an interval (α, β), in which

with a given probability the estimate ˆγ(θ) lays, then in this case we come to a

problem of an interval estimation. As a posteriori density f(θ/x

x) is the most

complete characteristic of the parameter θ at a given sample of observations

, . . . , x

), the problem of an interval estimation can be formulated as a

problem of a choice of an interval (α, β) of values θ, which in the best way

describes f(θ/x). In this case the loss function ϕ(θ; α, β) is a function of the

parameter θ and the interval. For example, the loss function can look like

ϕ(θ; α, β) =







(β − α)

, if θ ∈ (α, β),

(θ − α)

, if θ < (α, β),

(θ − β)

, if θ > (α, β),

Elements of mathematical statistics 87

and a posteriori loss is equal

θ/ξ

[ϕ(θ; α, β)] = w

(β − α)

f(θ/x

, . . . , x

)dθ

+ w

(θ − α)

f(θ/x

, . . . , x

)dθ

+ w

(θ − β)

f(θ/x

, . . . , x

)dθ.

The decision-making is connected with a value of an interval minimizing a

posteriori loss.

(E) From the practical point of view, the problem is important, in which it is

necessary to implement decision-making about a state of the object and to

yield an estimate of desired parameters, i.e. to combine the problems such as

A and B in one problem. As an example it is possible to give a problem of the

signal extraction with a simultaneous estimate of its parameters (an amplitude

and a time of the arrival).

The statistical classiﬁcation of foregoing problems consists in the following:

The problems such as A with two decisions are stated usually in the terms of

hypothesis checking, which should be accepted or is rejected. Such problems belong

to a wide class of problems, which is called the test of hypothesis.

The problems such as B, in which it is necessary to ﬁnd numerical value of

parameter, belongs to a class of problems of the point statistical estimation. Prob-

lems such as C, in which the interval covering an estimate of the parameter with

the given probability is determined, belongs to a class of problems of the interval

statistical estimation.

In the statistical theory of the interpretation of geophysical observations the

following classiﬁcation of foregoing problems is used.

(1) Problems such as A, in which it is necessary to determine a quantitative state of

geophysical object (there is a seismic signal on a given interval of a seismogram

or there is only seismic noise; whether there is a magnetized object of the

given shape or it is realization of a noise registered, for example, on a vertical

component of a magnetic ﬁeld etc.), have received a title of problems of the

qualitative interpretation.

(2) Problems such as B, in which the point parameter estimation of geophysical

objects (the determination of an amplitude and a time of the arrival of a seismic

signal; a ﬁnding of a magnetization and an occurrence depth of the upper edge

of a magnetic body; the determination of an electron concentration at given

height etc.) is called as problems of the quantitative interpretation or point-

quantitative interpretation.

88 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

(3) Problems such as C, in which the interval parameter estimation of geophysical

objects (the determination of an interval of the occurrence depth of a reﬂecting

seismic horizon; the ﬁnding of an interval of an occurrence depth of the upper

edge of the magnetized body; the determination of an interval for quantity of

an electron concentration at a given height etc.), is called as problems of the

interval-quantitative interpretation.

(4) It is necessary to estimate problems such as D, in which both a qualitative

state of the object, and parameters, describing it (a signal extraction together

with the determination of its parameters – an amplitude and a time of the

arrival; the detection of the magnetized body and the determination of its

parameters – magnetization, the occurrence depth etc.), is called as problems

of the quantitative-qualitative interpretation or by the combined interpretation.

2.1.3 Decision rule

The classical approach to a choice of a decision rule δ(

ξ) is based on a risk function

(θ). The best decision rule minimize the risk. Let δ

and δ

are two various

decision rules,

(θ) < R

(θ) for all θ,

then δ

is the best decision rule in the comparison with δ

Let’s consider an example of the analysis of three risk functions, which are

connected with three decision rules.

In a given range of values θ the decision rule δ

is more preferable than δ

. While

the decision rule δ

at some values of the parameter has the least value of a risk

function in the comparison with δ

and δ

, and at other values of the parameter it

is greater, it is impossible to ﬁnd a rule, which is the best at all θ, however at ﬁxed

θ it is possible to ﬁnd a sole best rule. The basic indeterminacy in a such choice is

arises from an unknown value of θ.

The decision rule δ (δ ∈ D) is called admissible, if the decision rule δ

(δ

∈ D)

with the inequality

(θ) ≥ R

(θ),

which is valid for all θ, does not exist. Thus, if the solving rule is admissible, then in

a class of the decision rules D the decision rule δ

does not exist, which is not worse

than δ for all θ. Usually admissible estimates meet much, therefore it is necessary

to oﬀer a criterion of a choice of the best rule among admissible rules.

Bayes strategy for a choice of a decision rule δ for a priori density f(θ) is based

on a function of a posteriori risk r

f(θ)

(δ). The best, from the point of view of the

Bayes strategy, is a decision rule relevant to the minimum of a posteriori loss

(B)

f(θ)

(

δ) ≤ r

f(θ)

(δ)

Elements of mathematical statistics 89

for arbitrary δ, or

δ = arg min

δ∈D

(θ)f (θ)dθ.

The minimum risk r

(B)

f(θ)

(

δ) is called the Bayes risk for a priori density f (θ). To

use this criterion, it is necessary to assume, that the parameter θ is a random one

and its a priori distribution is known. The knowledge of a such distribution is not

always possible in practice. Frequently f(θ) is interpreted as a weight function,

which is determined a degree of a signiﬁcance of various values of the parameter.

If a priori information about the parameter θ misses, it is expedient to view

a maximum of a risk function as its most important characteristic. Among two

functions is more preferable one which has the minimum value of a maximum of

risk. The decision strategy ensuring a minimum of the maximum risk are termed

the minimax procedure:

minmax

= arg

δ∈D

min max

θ∈Ω

(θ).

As the maximum designates most major (on the average) losses, which can arise at

the use of the given procedure, the minimax decision in the comparison with other

decisions gives the greatest protection against great losses.

Other criterion of a choice of the decision rule is based on the likelihood func-

tion. Let us consider a sample of n independent observations x

, x

, . . . , x

of the

components of a random vector ξ. As x

, x

, . . . , x

are independent, then a joint

density function is equal

L(x, θ) =

i=1

f(x

, θ).

The function L(

x, θ) is called the likelihood function for θ, if we consider it as a

function of the parameter θ or the vector parameter

θ at stipulated x

, x

, . . . , x

which are registered at an experiment.

If the decision is reduced to a problem of the determination of a value of the

parameter θ, then the natural estimate of θ can be picked on the basis of the con-

dition of the greatest probability at the given sample of experimental observations

, x

, . . . , x

, i.e. the estimate maximizes the likelihood function

MLM

= arg max

θ∈Ω

x, θ).

The method of an estimation, when an estimate of the parameter brings the

greatest value of the likelihood function is called as the maximum likelihood method.

Using the likelihood function, it is possible to formulate the procedure of a decision

not in the terms of a loss strategy, and in the terms of a winning strategy. The

winning is equal to zero (α(θ) = 0), in a case of the improper decision, and it

is positive α(θ) > 0, for the proper decision, where θ is a true quantity of the

parameter. Then it is advisable to supply the likelihood function with a weight

90 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

function connected with winnings, and to determine the value of θ, maximizing a

product α(θ)L(xx, θ).

If we consider θ as random variable and designate as α(θ) a priori distribution

of the parameter, then a posteriori distribution of parameter the θ is written

p(θ/x

x) =

α(θ)L(x

x, θ).

The maximization of a posteriori probability can be considered as a strategy of the

estimation

MAP

= arg max

θ∈Ω

p(θ/

x) = arg max

θ∈Ω

α(θ)L(x

x, θ)

(the multiplier p(xx) does not inﬂuence a value of the argument at the maximum

point of the likelihood function, therefore we have rejected it). The estimate

MAP

is called the maximum a posteriori probability estimate.

Consider a two-alternative problem. Let ω

and ω

designate a range θ, for

which d

and d

accordingly are the proper decisions and α(θ) = α

at θ ∈ ω

and

α(θ) = α

at θ ∈ ω

are valid. We make a decision d

, if

max

θ∈ω

L(xx, θ) < α

max

θ∈ω

L(x, θ),

max

θ∈ω

x, θ)

max

θ∈ω

L(x

x, θ)

and the decision d

, if

max

θ∈ω

L(xx, θ) > α

max

θ∈ω

L(x, θ),

max

θ∈ω

x, θ)

max

θ∈ω

x, θ)

A such procedure is called the likelihood ratio method. If θ it is possible to con-

sider as a random parameter, then α

and α

it is possible to interpret as a priori

probabilities of belonging of the parameter to the ﬁeld of ω

and ω

accordingly.

2.1.4 Suﬃcient statistic

A high proﬁle in the practical sense has such a transformation of observations

, . . . , x

, which gives in cutting number of experimental data, but thus the infor-

mation about parameter θ (with distribution f(xx, θ) )or vector of the parameters

θθ (with the distribution f(xx, θ)) is completely maintained. Such type of a trans-

formation is connected with the concept of the notion of the suﬃcient statistic

T (x

, . . . , x

), which contains the complete information on the parameter θ. The

statistics T (x) is called suﬃcient for θ, if the conditional density function xx at given

T is independent from θ, and T and θ can be multivariate and have various di-

mensionalities. The necessary and suﬃcient condition, that T (x) is the suﬃcient

statistic for θ, leads to the next writing down of the likelihood function

x, θ) = g(T, θ)h(x),

Elements of mathematical statistics 91

where h(x

x) does not depend from θ and g(T, θ) and it is proportional to f (T/θ),

which is the conditional density of T at the given parameter θ.

Example 2.4. Let ξ is in the accord with to the Gaussian distribution N(m

, σ

then the likelihood function

x, m

, σ

) = (2πσ

)

−n/2

exp

−

2σ

i=1

− m

)

= (2πσ

)

−n/2

exp

−

2σ

(¯x − m

)

exp

−

2σ

i=1

− ¯x)

where ¯x = (1/n)

i=1

. If σ

is known, then ¯x is in the accord with the Gaussian

distribution N(m

, σ

/n) and the likelihood function can be represented as

L(xx, m

) = g(¯x, m

)h(xx),

where

g(¯x, m

) = f(¯x, m

) =

2σ

1/2

exp

−

2σ

(¯x − m

)

h(x) = n

−1/2

(2πσ

)

−(n−1)/2

exp

−

2σ

i=1

− ¯x)

Consequently, ¯x is a suﬃcient statistic for m

. Using the suﬃcient statistics, we

reduce a volume of data, which is necessary for the parameter estimation. It is

especially essential in a case of a great information ﬂow.

Example 2.5. Let x

, . . . , x

are an independent components of vector ξξ with

Gaussian distribution. The likelihood function in this case reads as

L(xx, m

, σ

) = (2πσ

)

−n/2

exp

−

2σ

i=1

−

2σ

The factorization criterion shows that the statistics T(x) = (

) is suﬃcient

for σ

, m

, i.e. for the estimation of the parameters of the Gaussian distribution is

suﬃcient to have a sum of observations and a sum of squared observations. Thus,

it is necessary to store in a computer memory only two numbers —

and

that can appear essential at a great sample size n.

2.2 Estimate Properties

The wide class properties of important problems of processing of the geophysical

information brings to ﬁnding of estimates of desired parameters (an amplitude and

an arrival time of a seismic signal, a magnetization and an occurrence depth of

92 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

the magnetized body, an electron concentration at the given height etc.). Because

the estimate is a statistics, then to it the concept of the suﬃciency surveyed in

the Sec. 2.1.4 is applicable. The ﬁnding of the estimate is reduced to a choice of a

function according to the accepted criterion. The quality of a criterion is determined

by the following basic properties: a consistency, an unbiasedness, an eﬃciency and

a robustness.

2.2.1 Consistency

The estimate

for the parameter θ is termed a consistent, if

converges to a true

value of the parameter θ

with increasing of number of observations. It is possible to

deﬁne diﬀerent types of a competence, using various deﬁnition of convergence. In the

mathematical statistics at the deﬁnition of a consistency a probability convergence

is used more often. The estimate

is consistent one, if if there is such N for

arbitrary small ε > 0, η > 0 , that

P (|

− θ

| < ε) > 1 − η

for all n > N . In this case it is said, that

converges on the probability to θ

the increase n (Fig. 2.2).

Fig. 2.2 The illustration of the convergence in probability.

2.2.2 Bias

A bias b

(

θ) of the estimate

θ, obtained by n observations, means a divergence of

the mathematical expectation of the estimate of a true value of the parameter:

(

θ) = M[

] − θ

An estimate

θ is called unbiased, if for all n

(

θ) = 0 or M[

θ] = θ

At Fig. 2.3 a changing of the distribution function at the increasing of a number

of observations n (marked by arrow) under conditions of the consistency and the

unbias and without a such condition is demonstrated. Among the estimates of the