Troyan V., Kiselev Y. Statistical Methods of Geophysical Data Processing

Подождите немного. Документ загружается.

Basic concepts of the probability theory 33

1.5.3 Semi-invariants or cumulants

If for one-dimensional distribution the moments of s-th order exist, then semi-

invariants (cumulants) exist also, which are deﬁned as coeﬃcients κ

, κ

, . . . , κ

expansion of the logarithm of the moment generating function in Taylor series

ln α

(t) = κ

t + κ

+ κ

+ . . .

It follows that



∂

∂t

ln α

(t)



t=0

where κ

= m

, κ

= Dξ, κ

= µ

, κ

= µ

− 3µ

and so on.

1.5.4 Exercises

(1) To ﬁnd the characteristic function g

(t) of the random variable ξ with a prob-

ability density

(x) =

−|x|

(2) The random variable ξ has the characteristic function

(t) =

1 + t

To ﬁnd the density function of the random variable.

(3) The random variable ξ has the normal density function

(x) =

√

2πσ

exp

(

−

(x − m

)

2σ

)

To ﬁnd its characteristic function.

(4) Using the characteristic function to ﬁnd a composition of two normal distribu-

tions ξ ∈ N(0, σ

), η ∈ N(0, σ

). To ﬁnd g

(t) for ζ = ξ + η.

(5) The discrete random variable ξ satisﬁes to the Poisson’s distribution.

P (ξ = m) =

−a

To ﬁnd

(1) the characteristic function;

(2) M ξ and Dξ, with the use of g(z).

(6) To ﬁnd the characteristic function and the initial moments of a random variable

with the density function

(x) =



exp(−x) for x ≥ 0,

0 for x < 0.

(7) To ﬁnd the characteristic function and complete set of the initial moments of the

random variable which satisﬁes the uniform distribution at the interval (a, b).

34 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

(8) The random variable ξ has the density function

(x) = 2h

−h

(x ≥ 0).

To ﬁnd its characteristic function.

(9) To ﬁnd the characteristic function of the random variable with the density

function

(x) =

√

− x

(|x| < a).

(10) The random variable ξ satisﬁes to the Cauchy distribution

(x) =

(x − c)

+ a

To ﬁnd its characteristic function.

1.6 The Limit Theorems

The analysis of mass phenomena, which are randomicity ones, shows, that the

stability of the central tendency is observed, i.e. at major number of chance phe-

nomena their central tendency ceases to be random and can be predicted with a

major degree of the deﬁniteness.

This fact determines the physical content of the law of averages. The opportu-

nities of predictions in the ﬁeld of mass casual appearances are expanded, if it is

possible to ﬁnd the limiting laws. It allows to make by the group of the theorems

integrated under a title central limit theorems.

1.6.1 Convergence in probability

The random variable ξ

converges in probability to a quantity a, if at magniﬁcation

n the probability that ξ

and a will be arbitrary close, unrestrictedly close to 1. It

means, that at suﬃciently great n

P (|ξ

− a| < ε) > 1 − δ,

where ε and δ are arbitrary small values.

1.6.2 Chebyshev inequality

Let there is a random variable ξ with the mathematical expectation m

and variance

Dξ. For arbitrary α > 0 the follow inequalities are true

P (|ξ − m

| ≥ α) ≤

Dξ

(1.35)

(in the case of a discrete random variable ξ) and

P (|ξ − m

| > α) ≤

Dξ

(1.36)

Basic concepts of the probability theory 35

(in the case of a continuous random variable ξ). Let us prove an inequality (1.36)

for the case of a continuous random variable

P (|ξ − m

| > α) =

|ξ−m

|>α

(x)dx,

Dξ =

∞

−∞

(x − m

)

(x)dx =

∞

−∞

|x − m

(x)dx

≥

|x−m

|>α

|x − m

(x)dx.

Exchanging |x −m

| under the integral on α:

Dξ ≥ α

|x−m

|>α

(x)dx = α

P (|ξ − m

| > α),

we obtain the inequality (1.36).

1.6.3 The law of averages (Chebyshev’s theorem)

At suﬃciently large number of independent trials the arithmetic average of observed

random variables converges in probability to its mathematical expectation.

Let ξ is a random variable with the mathematical expectation m

and variance

Dξ. Let us consider n of such independent random variables ξ

, . . . , ξ

as a model

of the experiment with n independent trials of an initial random variable. Let us

write the arithmetic average n of these random variables

η =

i=1

The mathematical expectation m

and variance Dη look like

= Mη =

i=1

Mξ

= m

Dη =

i=1

Dξ

Let us note the Chebyshev’s theorem in the following form



i=1

− m



< ε

> 1 − δ. (1.37)

Proof. Let us consider the random variable η together with the Chebyshev in-

equality (1.35), by setting α = ε, we shall obtain

P (|η − m

| ≥ ε) ≤

Dη

Dξ

nε

36 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

Whatever small ε may be, it is possible to take n by such great, that the inequality

is fulﬁlled

Dξ

nε

< δ,

where δ is any small quantity. Then



i=1

− m



≥ ε

< δ,

or passing to complement event, we shall obtain



i=1

− m



< ε

> 1 − δ,

which was to be proved. 

1.6.4 Generalised Chebyshev’s theorem

If ξ

, ξ

, . . . , ξ

are independent random variables with the mathematical expecta-

tions

, m

, . . . , m

and the variances

, D

, . . . , D

and if all variances are restricted by the same quantity C

Dξ

< C (i = 1, 2, . . . , n),

That at increase of n the arithmetic average of the observed variables ξ

, ξ

, . . . , ξ

converges in probability to the arithmetic average of their mathematical expecta-

tions



i=1

−

i=1



< ε

> 1 − δ.

The proof is similar to the proof of the Chebyshev’s theorem for one random vari-

able.

1.6.5 Markov’s theorem

If ξ

, ξ

, . . . , ξ

are independent random variables, and if D(

i=1

)/n

→ 0 under

n → ∞, the arithmetic average of observed random variables ξ

, ξ

, . . . , ξ

converges

in probability to the arithmetic average of their mathematical expectations.

Basic concepts of the probability theory 37

Proof. Let us consider the random variable η having the variance Dη:

η =

i=1

, Dη =



i=1



Consider the random variable η together with the Chebyshev inequality

P (|η − m

| ≥ ε) ≤

Dη

As Dη → 0 under n → ∞, for suﬃciently great n, then

P (|η − m

| ≥ ε) < δ,

or passing to complement event, we shall obtain

P (|η − m

| < ε) = P



i=1

−

i=1



< ε

> 1 − δ.



1.6.6 Bernoulli theorem

Let n of independent trials are carry out. The probability of realization of the event

A in the each trial is equal p. The Bernoulli theorem states, that at unbounded

increasing of number of the trials n the frequency of occurrence ep the events A

converges in probability to the probability of its realization p,

P (|ep − p| < ε) > 1 − δ,

where ε and δ are arbitrary small positive numbers.

1.6.7 Poisson theorem

Let n of independent trials are carry out. The probability of occurrence of the

event A in i trial is equal p

. Under increasing of n the frequency of occurrence of

A converges in probability to the arithmetic average of probabilities p



ep −

i=1



< ε

> 1 − δ.

The Poisson theorem is important for the practical application of the probability

theory, as it takes into account various experimental conditions.

1.6.8 The central limit theorem

If ξ

, ξ

, . . . , ξ

are independent random variables having the same distribution law

with the mathematical expectation m

and the variance σ

, then at unrestricted

increase of n the distribution law of the sum η

i=1

comes arbitrary close to

the normal distribution.

38 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

Proof. According to the property of the characteristic function

(t) = [g

(t)]

The ﬁrst three terms of expansion of g

(t) in a Maclaurin’s series in a vicinity of

t = 0 read as

(t) ≈ g

(0) + g

(0)t + [g

(0)/2 + α(t)]t

where α(t) → 0 under t → 0, g

(0) = 1, g

(0) = im

, let m

= 0, then g

(0) = 0,

(0) = −σ

. To rewrite the expression of g

(t) with the use of the formulae of

(0), g

(0) and g

(0):

(t) = 1 −



− α(t)



Let us introduce a normalized random variable ζ

= η

/(σ

√

n). Let us show,

that the characteristic function η

under increasing of n tends to the characteristic

function of the normal law

(t) = g



√







√



or, using expansion of g

(t), we obtain

(t) =



1 −



− α



√





After taking the logarithm of g

(t) and introducing a notation

β =



− α



√



we can obtain

ln g

(t) = n ln(1 − β).

At increasing of n β will tend to zero, then it is possible to be restricted to the ﬁrst

term of the expansion

ln(1 − β)≈ − β.

Passing to a limit

lim

n→∞

ln g

(t) = lim

n→∞

n(−β) = lim



−

+ α



√





lim

n→∞



√



= 0, and lim

n→∞

ln g

(t) =

−t

we obtain

lim

n→∞

(t) = exp



−t



but this expression is the characteristic function of the normal law with parameters

= 0, σ

= 1. 

Basic concepts of the probability theory 39

1.6.9 Exercises

(1) Using the Chebyshev inequality to ﬁnd the upper estimate of the probability

that the random quantity ξ, having an ensemble average m

and variance σ

will deviate from m

on value less than 3σ

(2) The large number n of independent trials is yielded, in each of trial we have

the realization of the random variable ξ, which has a uniform distribution at

an interval (1, 2). We shall consider the arithmetic average η =

i=1

/n of

observed quantities of a random variable ξ. On the basis of the law of averages

to ﬁnd out, to what number a the value η will converge in probability under

n → ∞. To estimate a maximum (practically possible) error of the equality

η ≈ a.

(3) The sequence n of random variables ξ

, ξ

, . . . , ξ

, which have a uniform dis-

tribution in intervals (0, 1), (0, 2), . . . , (0, n) is considered. What will happen

to their arithmetic average η =

i=1

/n under increasing of n?

(4) The random variables ξ

, ξ

, . . . , ξ

are distributed uniformly on the intervals

(−1, 1), (−2, 2), . . . , (−n, n). Whether will be arithmetic average η =

i=1

of random variables ξ

, ξ

, . . . , ξ

to converge in probability to zero under in-

creasing of n?

(5) At the spaceship the geiger for the deﬁnition of a number of hitting of the

cosmic particles with the spaceship for some interval of time T is installed.

The stream of cosmic particles is the Poisson ﬂow (exponential arrivals) with

the intensity λ, each particle is registered by the geiger with probability p. The

geiger is switched on for the random time T which value is distributed under

the exponential law with parameter µ. A random quantity ξ is a number of

the registered particles. To ﬁnd a distribution law of a random variable ξ.

1.7 Discrete Distribution Functions

The distribution law (distribution series) of discrete random variable is called a

set of its possible values and the probabilities, which correspond to them. The

distribution law of a discrete random variable can be given as the table (Table 1.1)

where

= 1, or in analytic form

P (ξ = x

) = ϕ(x

The distribution law can be represented by graph (Fig. 1.25).

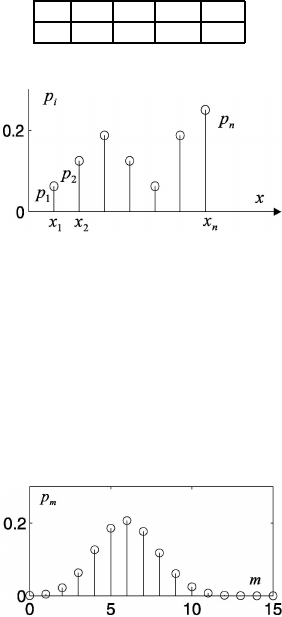
40 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

Table 1.1 Representation of

the distribution law of a dis-

crete random variable.

ξ x

. . . x

P p

. . . p

Fig. 1.25 Graphic presentation of the probability distribution of the discrete random variable.

1.7.1 Binomial distribution

The random variable ξ has the binomial distribution, if its possible quantities 0, 1,

. . . , m, . . . , n correspond to the quantities of probability

= P (ξ = m) = C

n−m

, (1.38)

where 0 < p < 1, q = 1 − p, m = 0, 1, . . . , n (Fig. 1.26). The binomial distribution

Fig. 1.26 Binomial distribution (p = 0.4, n = 15).

depends on two parameters n and p.

• Mathematical expectation Mξ = np.

• Variance Dξ = np(1 − p).

• Asymmetry coeﬃcient γ

= (1 − 2p)/[np(1 −p)]

1/2

• Excess γ

= [1 − 6p(1 − p)]/[np(1 −p)].

The binomial distribution gives the probability of m successful trials at total number

of trials n, when the probability of a success in one trial is equal p.

Example 1.14. Probability to register a stream of ultrarays in a given energy

range (event A) using one satellite observation is equal p. To ﬁnd a number of

observations such, that the probability of the occurrence even one event A is equal

α. So, it is necessary to ﬁnd n, for which

P (ξ ≥ 1) ≥ α,

Basic concepts of the probability theory 41

1 − P (ξ = 0) ≥ α, P (ξ = 0) ≤ 1 − α.

Using formula (1.38) under m = 0, we obtain

(1 − p)

≤ 1 − α,

whence

n ≥ ln(1 − α)/ ln(1 − p).

1.7.2 Poisson distribution

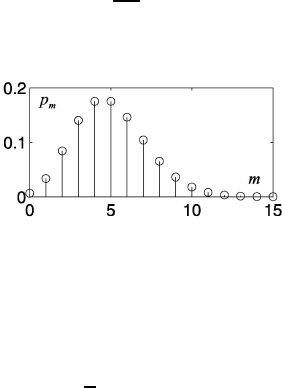
The discrete random variable ξ has the Poisson distribution, if the probability of

ξ = m (m = 0, 1, . . . , m, . . . ) can be given by the formula

= P (ξ = m) =

−a

, m = 0, 1, 2, . . . , (1.39)

where a > 0 (Fig. 1.27).

Fig. 1.27 Poisson distribution (a = 5).

The Poisson distribution depends on one parameter a.

• Mathematical expectation Mξ = a.

• Variance Dξ = a.

• Asymmetry coeﬃcient γ

= 1/

√

• Excess γ

= 1/a.

The Poisson distribution gives the probability of observation of m events in a given

time interval, on condition that the events are independent. This distribution is

an extreme case for a binomial distribution at p → 0, n → ∞, if np = a = const.

The Poisson distribution can use approximately in cases, when the major number of

independent trials are carried out and the stated event happens to small probability.

The Poisson distribution is used for the description of the ﬂow of events. The ﬂow of

events is called a sequence of homogeneous events occurring one behind another in

random time. The average of events λ per unit time, is called a rate of occurrence.

The value λ can be both stationary value, and variable.

The ﬂow of events is called the ﬂow without a consequence, if the probability of

hit of this or that number of events on any time interval does not depend on that,

how many events have hitted on any other interval, not traversed with it.

42 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

The ﬂow of events is called ordinary, if the probability of the occurrence on a

elementary interval ∆t of two or more events is a negligible quantity in comparison

with the probability of occurrence of one event.

The ordinary ﬂow of events without consequences is called the Poisson ﬂow. If

the events produce the Poisson ﬂow, then the number ξ of events hitting on any

time slice (t

, t

+ τ) has the Poisson distribution

−a

(m = 0, 1, 2, . . . ),

where a is the mathematical expectation of a number of hitting into time slice:

a =

+τ

λ(t)dt.

If λ = const, the Poisson ﬂow is called a stationary ﬂow, in this case of a number

of events hitting on a time slice τ, has the Poisson distribution with the parameter

a = λ/τ.

The Poisson ﬂow can be used for the description of an arrival time of seismic

waves on a seismogram. It is possible to show, that the number of wave events

for great number practically of interesting cases is well described by the Poisson

distribution.

Example 1.15. At a seismogram there is a reﬂected wave train produced by a

layered unit, which is a stationary Poisson ﬂow with the intensity λ is ﬁled. To ﬁnd

the probability that during τ there are following events:

(1) A (nothing arrivals);

(2) B (no less than three arrivals);

(3) C (three arrivals).

Mathematical expectation of number of waves is a = λτ , then

P (A) = P

= e

−λτ

, P (C) = ((λτ)

/3!)e

−λτ

P (B) = 1 − (P

+ P

) = 1 − e

−λτ

[1 − λτ − 0.5(λτ )

1.7.3 Geometrical distribution

The random variable ξ has the geometrical distribution, if its possible quantities

are equal 0, 1, 2, . . . , m, . . . , and the probabilities of these quantities are given by

the formula

= q

m−1

p (m = 0, 1, 2, . . . ), (1.40)

where 0 < p < 1, q = 1 − p (Fig. 1.28). The geometrical distribution gives prob-

ability to get m unsuccessful trials before the ﬁrst successful trial provided that

probability of success in one trial is equal p. The probability p

for a series of se-

quential quantities m forms an indeﬁnitely decreasing geometrical progression with

a denominator q.