Troyan V., Kiselev Y. Statistical Methods of Geophysical Data Processing

Подождите немного. Документ загружается.

Basic concepts of the probability theory 23

1.4 The Numerical Characteristics of Probability Distributions

Let (Ω, A, P ) a ﬁnite probabilistic space and ξ = ξ(ω) is a random variable with

the values belonging to a set X = {x

, . . . , x

}. If A

= {ω : ξ = x

} (i = 1, . . . , n),

then ξ is possible to represent as

ξ(ω) =

i=1

I(A

), I(A

) =



1 ω ∈ A

0 ω 6∈ A

where A

, . . . , A

is a dissection of the space Ω, i.e. pairwise are not intercrossed,

and their sum is equal Ω.

1.4.1 Mathematical expectation

Mathematical expectation, or (expectation, expected value, mean of distribution) of

a random variable ξ =

i=1

I(A

), is named a value

Mξ =

i=1

P (A

To take into account A

= {ω : ξ(ω) = x

} and P

) = P (A

), we can obtain

Mξ =

i=1

). (1.23)

If the random variable ξ ∈ R

is continuous one, its mathematical expectation

is deﬁned as

Mξ =

∞

−∞

(x)dx. (1.24)

The mathematical expectation is a measure of location of a random variable ξ

and characterizes “center” of its distribution. The examples of the density functions

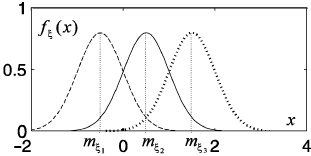
with various mathematical expectations is given in a Fig. 1.14.

Fig. 1.14 Normal density functions with various mathematical expectation. Mathematical ex-

pectation: m

= −0.5, m

= 0.5, m

= 1.5. Standard deviation: σ

= σ

= 0.5.

The mathematical expectation of a random variable has the following properties:

(1) if ξ ≥ 0, then Mξ ≥ 0;

24 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

(2) M (aξ + bη) = aMξ + bM η, a and b are constants;

(3) if ξ ≥ η, then Mξ ≥ Mη;

(4) |M ξ| ≤ M |ξ|;

(5) if ξ and η are independent variables, then M(ξ · η) = Mξ · Mη;

(6) (M (ξ · η))

≤ Mξ

· Mη

is the Cauchy–Bunyakovskii inequality.

Along with the entered above name of the mathematical expectation, the fol-

lowing names are used: hξi, m

For a function of the random variable ϕ(ξ) the mathematical expectation is

deﬁned as

Mϕ(ξ) =

ϕ(x

) (1.25)

(for a discrete case) and

Mϕ(ξ) =

∞

−∞

ϕ(x)f

(x)dx (1.26)

(for a continuous case).

1.4.2 Variance and correlation coeﬃcients

The variance of a random variable ξ(ω) is deﬁned as

Dξ = M(ξ − Mξ)

. (1.27)

The value σ

√

Dξ is named the standard deviation or mean-square deviation.

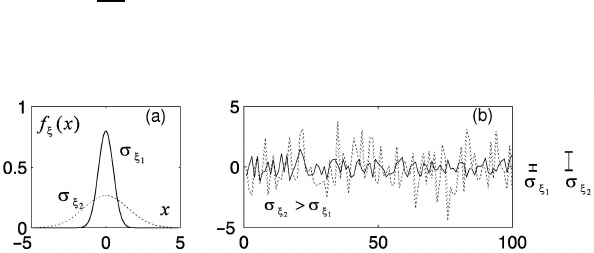
The examples of uncorrelated Gaussian time series with various standard deviations

are given in Fig. 1.15.

Fig. 1.15 Normal density functions (a) and uncorrelated time series, answering them, (b). Math-

ematical expectation: m

= m

= 0. Standard deviation: σ

= 0.5, σ

= 1.5.

The variance of a random variable has the following properties:

(1) Dξ = Mξ

− (Mξ)

;

(2) D(ξ) ≥ 0;

(3) D(a

+ a

ξ) = a

Dξ, a

and a

are constants. Da

= 0,

D(a

ξ) = a

Dξ;

Basic concepts of the probability theory 25

(4) D(ξ + η) = M ((ξ − Mξ) + (η − Mη))

= Dξ + Dη + 2M (ξ − Mξ)(η − M η).

Let us deﬁne cov(ξ, η) = R

ξη

= M(ξ − M ξ)(η − Mη). This quantity is named as a

covariance of random variables ξ and η (frequently for the covariance use a notation

ξη

). As Dξ > 0, Dη > 0, it is possible to introduce a normalized covariance

r(ξ, η) =

cov(ξ, η)

√

Dξ

√

Dη

, (1.28)

which is named a correlation coeﬃcient of the random variables ξ and η. The

correlation coeﬃcient varies inside an interval

−1 ≤ r(ξ, η) ≤ 1,

And the sign of an equality is reached under condition of, if ξ and η are connected

by a linear dependence

η = a

ξ + a

If a

> 0, then r(ξ, η) = 1. If a

< 0, then r(ξ, η) = −1. If ξ and η are

independent, then

cov(ξ, η) = M(ξ − Mξ) · M(η − Mη) = 0.

For independent ξ and η the variance of the sum is equal to the sum of variances:

D(ξ + η) = Dξ + Dη.

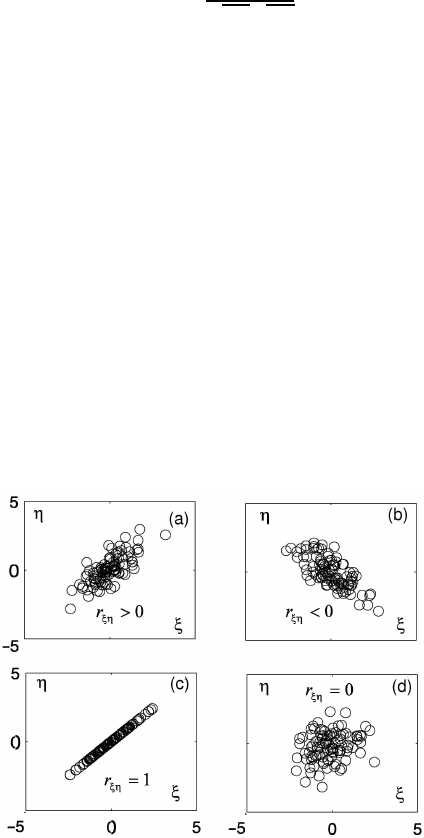
The samples of a normal bivariate distribution at various values of the correlation

coeﬃcient are represented at Fig. 1.16. Taking into account the deﬁnition of a

Fig. 1.16 Graphic representation of the samples from two-dimensional Gaussian distribution ξ

and η. Mξ = Mη = 0; r

ξη

= 0.75 (a); r

ξη

= −0.75 (b); r

ξη

= 1 (c); r

ξη

= 0 (d). Sample size is

equal 100.

26 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

covariance, the mathematical expectation of the product of random variables ξ and

η is possible to write as

M(ξ · η) = Mξ · Mη + cov(ξ, η).

In the case of uncorrelated random variables is valid M(ξ · η) =

= Mξ ·Mη. The variance of a linear function of random argument ξ

(i = 1, . . . , n)

becomes

i=1

+ a

i=1

Dξ

+ 2

i<j

cov(ξ

, ξ

If ξ

and ξ

uncorrelated, then

i=1

+ a

i=1

Dξ

If ξ and η are independent random variables, then

D(ξ · η) = Dξ · Dη + M ξ · Dη + Mη · Dξ.

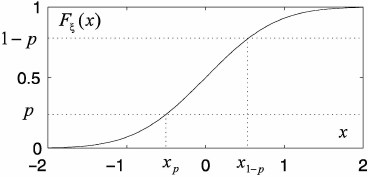
1.4.3 Quantiles

The quantile of order p of one-dimensional distribution is such a value x

of the

random variable ξ, for which

P (ξ < x

) = F

) = p, 0 < p < 1,

(Fig. 1.17).

Fig. 1.17 Distribution function and quantiles of the orders p and 1 − p. Normal distribution:

= 0, σ

= 1.

A value x

1/2

is named as a median of a distribution (Fig. 1.18). The geometrical

sense of the median is an abscissa of a point, in which area under the density curve

is bisected. Quartile x

1/4

, x

1/2

, x

3/4

, decile x

0.1

, x

0.2

, . . . , x

0.9

and percentile x

0.01

0.02

, . . . , x

0.99

divide a domain of variation of x accordingly into 4, 10 and 100

intervals, the hits in which have the equal probabilities (Fig. 1.19).

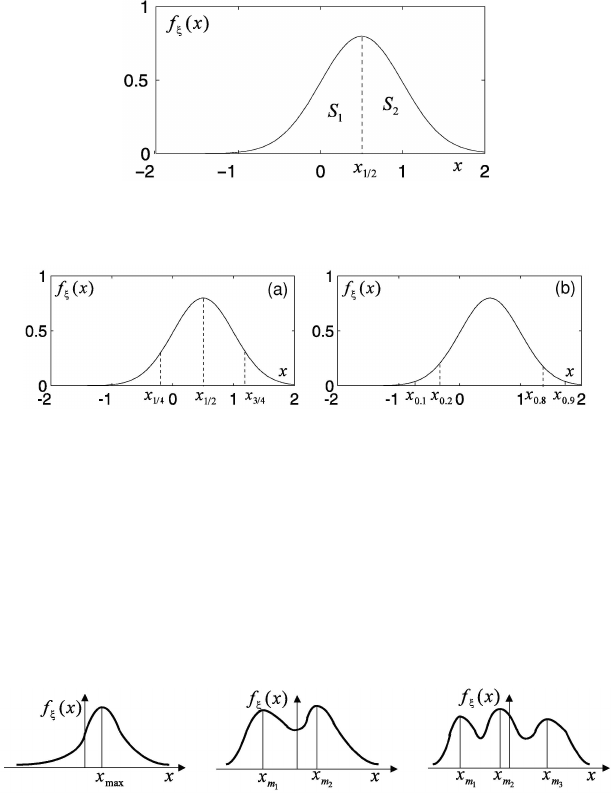
Basic concepts of the probability theory 27

Fig. 1.18 The density function and the median. Normal distribution: m

= 0.5, σ

= 0.5.

Fig. 1.19 The density function and its characteristics: quartiles (a) and deciles (b). Normal

distribution: m

= 0.5, σ

= 0.5.

1.4.4 Characteristics of a density function

The characteristic of location of a distribution of a random variable ξ in addition

to the mathematical expectation Mξ and the median x

1/2

is the mode of a con-

tinuous distribution, which is a point of a maximum of the density function. The

distributions having one, two and more modes, is named one-modal, two-modal

and multimodal (Fig. 1.20). In addition to the entered above variance Dξ and a

Fig. 1.20 The density functions with a various number of the modes.

standard deviation σ

, as the characteristics of a dispersion of a random variable ξ

are used the following quantities:

• coeﬃcient of variation σ

/M ξ;

• mean absolute deviation M |ξ − M ξ|;

• interquartile distance x

3/4

− x

1/4

(Fig.1.21);

• 10 — 20 percent distance x

0.9

− x

0.1

For a discrete random variable is determined the range |x

max

− x

min

| of the

probability series P

) (Fig. 1.22).

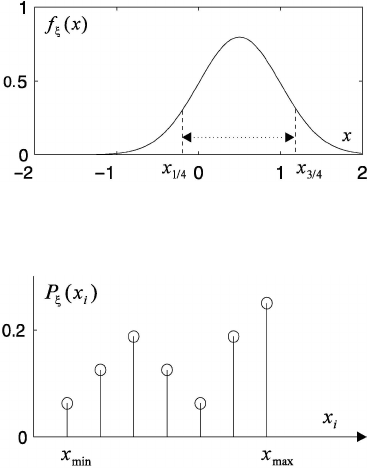
28 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

Fig. 1.21 Density function and interquartile distance. The normal distribution: m

= 0.5, σ

0.5.

Fig. 1.22 Probability distribution of a discrete random variable and the range.

The initial moment of the random variable ξ of s range is called the mathematical

expectation of s power of the random variable:

= Mξ

The centered random variable is called the random variable ξ − M ξ. The Central

moment of a range s is called the mathematical expectation of s power for the

centered random variable

(ξ) = M(ξ − Mξ)

at s = 2 we get a value of a variance Dξ. There is a connection between the initial

and central moments

= 0,

= α

− m

= α

− 3m

+ 2m

. . . . . . . . . . . . . .

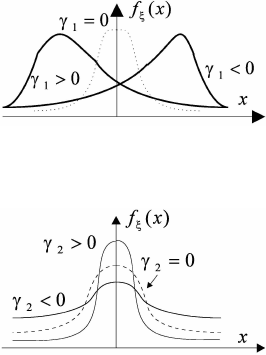
The third central moment µ

characterizes an asymmetry of a distribution. If the

distribution is symmetrical with respect to m

, all moments of the odd order are

equal to zero. Therefore as a measure of the asymmetry is taken the third moment.

A nondimensional asymmetry coeﬃcient is introduced: γ

= µ

/σ

, Fig. 1.23. The

fourth central moment use as a characteristic of “steepness” or peakedness of the

Basic concepts of the probability theory 29

Fig. 1.23 Density functions with diﬀerent asymmetry coeﬃcients.

Fig. 1.24 A density function and excess.

density function. An excess of a random variable is introduced: γ

= (µ

/σ

) −3

(Fig. 1.24). Let us note, that for the normal distribution the equality µ

/σ

= 3

is valid. So the excess is a measure of a diversion from a normal distribution, for

which it is equal to zero. If the density curve is more peaked one, than in case of

the normal distribution, then γ

> 0, if the density curve is more ﬂat-topped one,

then γ

< 0.

1.4.5 Exercises

(1) The random variable ξ obeys the binomial distribution

P (ξ = m) = C

(1 − p)

n−m

, m = 0, 1, . . . , n.

To ﬁnd an mathematical expectation and variance of a random variable η =

exp(aξ).

(2) The J-scope of a navigation system, which works on a geophysical vessel, is a

circle of radius a. Owing to noises the stain with center in any point of this circle

can appear. To ﬁnd the mathematical expectation and variance of a distance

of the center of a stain from center of a circle.

(3) The random variable ξ has a density function f

(x) =

= 0.5 · sin x in an interval (0, π). Outside of this interval f

= 0 is valid.

To ﬁnd the mathematical expectation of η = ξ

(4) The random variable ξ has the density function f

(x) = 2 cos 2x in an interval

(0, π/4). Outside of this interval f

(x) = 0 is valid. To ﬁnd the mode and

median of ξ.

(5) To prove, that the mathematical expectation of a continuous random variable

is enclosed between its least and greatest values.

30 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

(6) The random variable ξ has a density function

(x) =



exp(−x)/n!, x ≥ 0,

0, x < 0.

To ﬁnd the mathematical expectation and variance.

K e y . It is expedient to take the expression for the gamma-function

Γ(n) =

∞

−x

dx.

(7) To prove, that if the random variables η and ξ are interlinked by a linear relation

η = a

ξ + a

, their correlation coeﬃcients are equal (±1) depending on a sign

(8) To prove, that for any random variables |r

ξη

| ≤ 1 is valid.

(9) The random variable ξ is in accord with the normal distribution with the math-

ematical expectation m

= 0. The interval (α, β), not including the coordinate

origin is given. At what value of the standard deviation σ the probability of hit

of a random quantity ξ into an interval (α, β) will reach a maximum.

(10) The random variable ξ is in accord with the normal distribution with the math-

ematical expectation m

and variance σ

. It is required to exchange the normal

distribution by the uniform distribution in an interval (α, β) approximately.

The cell boundary α and β should be selected so that to remain a constant the

mathematical expectation and variance of random variable ξ.

1.5 Characteristic and Generating Functions

The characteristic function of a random variable ξ is called the following function

g(t) = M(exp(itξ)), (1.29)

where i is the imaginary unit. If ξ is a discrete random variable, its characteristic

function is written as

g(t) =

k=1

exp(itx

). (1.30)

If ξ is a continuous random variable with the density function f

, its characteristic

function looks like

g(t) =

∞

−∞

exp(itx)f

(x)dx. (1.31)

The expression (1.31) is possible to consider (accurate to a sign of an exponent

of an exponential curve) as the Fourier transform of a density function. Then the

Basic concepts of the probability theory 31

calculation of a density function f

(x) using the known characteristic function is

reduced to the inverse Fourier transform:

(x) =

∞

−∞

exp(−itx)g(t)dt. (1.32)

Properties of the characteristic functions:

(1) If ξ and η are interlinked by the relation η = aξ (a is a constant), then

(t) = g

(at),

(t) = M exp(itη) = M exp(itaξ) = M exp(i(at)ξ) = g

(at).

(2) The characteristic function of the sum of independent random variables is

equal to product of characteristic functions of addends. Let ξ

, ξ

, . . . , ξ

are

independent random variables with characteristic functions g

(t), g

(t), . . . ,

(t), then the characteristic function of their sum η =

k=1

looks like

(t) = M(exp(itη)) = M

exp

= M

exp(itξ

)

(t).

(3) Let ξ and η are independent random variables with the distributions f

(x)

and f

(y) accordingly. Let us discover a density function of a random variable

ζ = ξ + η. In subsection 1.3.7 is shown, that density function f

(z) is a result

of the convolution of the density functions f

(x) and f

(y), that answers a

product of the appropriate characteristic functions, i. e.

(t) = g

(t) · g

(t).

The density function f

(z) can be obtained, by taking the inverse Fourier

transform of the function g

(t)

(z) =

∞

−∞

(t) exp(−itz)dt,

being product of characteristic functions g

(t) and g

(t).

1.5.1 Moment generating function

The set of the moments {α} characterizes the distribution of a random variable. It

is expedient to enter a function, which would depend on all moments and would

give a simple technique of a ﬁnding of the moment of any order.

The generating function of the initial moments of the random variable ξ is called

the function

(t) = M(exp(ξt)) =











∞

−∞

exp(xt)f

(x)dx, continuous r.v.,

k=1

exp(x

t)P

), discrete r.v.

32 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

After decomposition an exponential curve in a series, we shall obtain

(t) = M



1 + ξt +

(ξt)

+ . . .



= 1 + α

t + α

+ α

+ . . . (1.33)

So, the initial moment about s is a coeﬃcient at t

/s! in expression (1.33). The

second technique of a ﬁnding of the initial moment about s using a generating

function of the moments is reduced to the diﬀerentiation α

(t) on t s times:

∂

(t)

∂t

∞

−∞

exp(xt)f

(x)dx,

from which

∂

(t)

∂t



t=0

∞

−∞

(x)dx. (1.34)

The generating function of the central moments of random variable ξ is similarly

deﬁned:

(t) = M [exp{(ξ −m

)t}] .

After decomposition an exponential curve in a series, we shall obtain

(t) = M



1 + (ξ −m

)t + (ξ − m

)

+ . . .



= 1 + µ

+ µ

+ . . .

The central moment µ

is the coeﬃcient at t

/s!.

1.5.2 Probability generator

Probability generator is called the function

(t) = M(t

) =











∞

−∞

(x)dx, continuous r.v.,

k=1

), discrete r.v.,

where G

(1) = 1 by the normality condition. It is easy to establish a connection

of the probability generator with the moments. Having designated ∂G/∂t through

, we shall obtain

= G

(1), α

= G

(1) + G

(1),

= G

000

(1) + 3G

(1) + G

(1) . . . ,

and for the variance

= Dξ = G

(1) + G

(1) − [G

(1)]