Troyan V., Kiselev Y. Statistical Methods of Geophysical Data Processing

Подождите немного. Документ загружается.

Basic concepts of the probability theory 3

Fig. 1.3 Intersection of two subsets.

Deﬁnition 1.5 (Complement). The complement

A for a set of A (Fig. 1.4) is

the set containing all elements of Ω that do not belong A. The diﬀerence B \A is a

set containing the elements of B that are not in A. Then

A = Ω \ A is event, that

A does not occur.

Fig. 1.4 The set

A is the complement of the set A.

Example 1.6. If the set A = {HH, HT, TH}, then the event

A = {TT} consists of

a sequential appearance of two “tails”. The sets

A and A do not have the common

elements, hence the intersection A ∩

A is an empty set, i.e. A ∩

A = ∅.

In the probability theory the set ∅ is called the impossible event and the set Ω

is called the certain event.

A class of subsets A is called algebra of events, if it satisﬁes the following prop-

erties

(1) Ω ∈ A (the certain event is contained in A );

(2) ∅ ∈ A (the impossible event is contained in A );

(3) if A ∈ A, then

A ∈ A (

A = Ω \ A) (is closed under complement);

(4) if A

∈ A and A

∈ A, then A

∪A

∈ A and A

∩A

∈ A (is closed under the

union and intersection).

If the set Ω is ﬁnite one, then A coincides with the class of all subsets of Ω.

4 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

Consider the random experiment of measurement of a value ζ, for example,

the magnetizing force of the Earth. Let the elementary event is (ζ = x), where x

speciﬁed quantity. The set of elementary events can be identiﬁed with the point set

in the real axis. If it is known a priori, that ζ can take up the values from some

set of X, this set should be considered as the set of the elementary events. It is

natural to guess a possibility of observation of event {a ≤ ζ < b}, where a < b are

the arbitrary numbers. The ﬁnite sums of such half-intervals can be considered as

the algebra of events, connected with the experiment.

1.1.2 Probability model with a ﬁnite number of outcomes

Probability model with a ﬁnite number of outcomes includes:

(1) space of elementary events Ω;

(2) subset system A, which is constituted the algebra of events;

(3) probability p(ω

) of outcomes ω

, ω

∈ Ω (i = 1, . . . , n) (p(ω

) is “weight” of

elementary event) with the properties:

(1) 0 ≤ p(ω

) ≤ 1 (nonnegativeness);

(2) p(ω

) + ···+ p(ω

) = 1 (normalization).

The probability P (A) of an arbitrary event A for the case of A ∈ A is equal to the

expression

P (A) =

{i: ω

∈A}

p(ω

A triad (Ω, A, P ) determines the probability model or probability space of an exper-

iment with the outcome space Ω = {ω

, . . . , ω

} and with the algebra of events

From above axioms we conclude that:

(1) the probability of impossible event is equal zero P (∅) = 0;

(2) the probability of certain event is equal 1 P (Ω) = 1;

(3) P (A

∪ A

) = P (A

) + P (A

) − P (A

∩ A

);

if the events A

and A

are mutually exclusive events, i. e. A

∩ A

= ∅, then

P (A

+ A

) = P (A

) + P (A

);

(4) for A

⊂ A

is valid an inequality P (A

) ≤ P (A

);

(5) P (

A) = 1 − P (A);

(6) if A

, A

, . . . , A

are the pairwise disjoint events, then

P (

i=1

) =

i=1

P (A

);

(7) for arbitrary A

, A

, . . . , A

an inequality

P (

i=1

) ≤

i=1

P (A

)

is valid;

Basic concepts of the probability theory 5

(8) consider the events A

, A

, . . . , A

and introduce denotation

...i

= A

. . . A

. The following formula is valid

P (

i=1

) =

i=1

P (A

) −

i<j

P (A

) + ···

+ (−1)

k−1

<···<i

P (A

...i

) + ··· + (−1)

n−1

P (A

1...n

1.1.3 Relative-frequency deﬁnition of probability

Consider of a sequence of n random experiments. Let’s designate their outcomes

by points ω

, . . . , ω

in the space of elementary events Ω. Let’s A is the algebra of

events A ∈ A, which are observed during experiment. Let’s designate a number of

occurrence of event A after n experiments as K

(A). If ω

∈ A, then A occurs after

i-th experiment. A value

(A) = K

(A)/n

is named a frequency of occurrence of event A after n experiments. The frequency

of event sometimes term as statistical probability. At magniﬁcation of number of

experiments the frequency ν

(A) tends to the probability of event A.

1.1.4 Classical deﬁnition of probability

Consider an experiment with a complete group of the elementary events

, E

, . . . , E

, which are the components of the set Ω. Then each event from

A looks like

A =

k=1

where (i

, i

, . . . , i

) is a subset of Ω. By using the properties of probability pairwise

of not intersected events, we get the formula

P (A) =

k=1

P (E

Hence, in case of the ﬁnite experiment the probability of any event is determined by

probabilities of elementary events. For example, taking into account a symmetry of

experiment, it is possible to establish a priori, that the elementary events have an

equal probability (the probability of the elementary event is equal 1/n, where n is a

number of equally possible outcomes), and the probability of event A is calculated

as the relation of number of the favorable outcomes m to number of equally possible

outcomes n:

P (A) =

6 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

Usually calculation of equally possible and favorable outcomes is carried out by the

combinatorial methods

Such deﬁnition is possible to subject to criticism on the ground that the notion

equally possible actually means equality probability, and reasoning, thus, contains a

vicious circle.

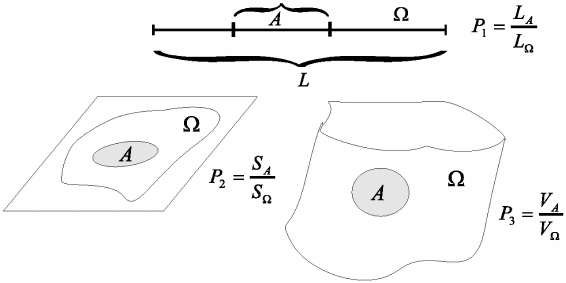
1.1.5 Geometrical deﬁnition of probability

In case of experiments with inﬁnite number of equally possible outcomes, when the

eﬀect(result) of the experiment can be connected with a point belonging to R

, the

probabilities of some events can be deﬁned geometrically as the relation of Euclidean

volume (area, length) for the part of a ﬁgure to volume (area, length) of complete

ﬁgure. An illustration of geometrical deﬁnition of probability is given on Fig. 1.5.

Fig. 1.5 An illustration of geometrical deﬁnition of probability.

1.1.6 Exercises

(1) Two bones are thrown. To ﬁnd probability that the total number of pips on

the happen to be facets is even, and on a facet even by one of bones will appear

six pips.

(2) In the container there are 10 identical devices marked with the numbers

1, 2, . . . , 10. The six devices are taken arbitrary. To ﬁnd probability that among

the extracted devices will appear: a) the device with the number 1; b) devices

with the numbers 1 and 2.

(3) In a batch from N geophones n geophones are standard ones. The m receivers

is selected randomly. To ﬁnd probability that among select receivers k receivers

are standard ones.

(4) The parallel lines are drown on the plane. The distance between the lines is

2a. A needle of length 2l (l < a) is thrown on the plane randomly. To ﬁnd the

Basic concepts of the probability theory 7

probability that the needle will intercross any line.

(5) On a line segment OA with the length L of a numerical axis 0x are arbitrary

marked two points B(x

) and C(x

). To ﬁnd probability that it is possible to

construct a triangle using three obtained segments.

(6) In the sound detector the signals from two sources are received. An inﬂow of

each of signals is equally possible at any moment of time interval by duration

T . There is snap into action, if the diﬀerence between the arrival time of signals

is equal t (t < T ). To ﬁnd probability that the sound detector will work into

time T , if each of sources will send one signal.

(7) From a course of the statistical physics it is known, that the indiscernible ulti-

mate particles (electrons, protons, neutrons) satisfy the Pauli’s exclusion prin-

ciple and statistics of Fermi - Dirac. To ﬁnd a number of possible outcomes of

allocation n on M states. (Is possible to use analogy of allocation of n bodies

on M without returning.)

(8) Photon and π-meson satisfy to the Bose-Einstein statistics and these particles

are considered as indiscernible and do not submit to the Pauli’s exclusion prin-

ciple. To ﬁnd a number of possible outcomes of allocation n of particles on M

states. (It is possible to use analogy of allocation of n indiscernible bodies on

M boxes.)

1.2 Basic Properties of Probability

1.2.1 Addition of probabilities

If A

and A

are two mutually exclusive sets, the probability of their sum is equal

to the sum of probabilities:

P (A

+ A

) = P (A

) + P (A

), (1.1)

or for A

, A

, . . . , A

P (

i=1

) =

i=1

P (A

). (1.2)

If A

and A

have common elements, i.e. the elementary events ω

can belong both

and A

P (A

+ A

) = P (A

) + P (A

) − P (A

), (1.3)

and for an arbitrary number of sets A

, A

, . . . , A

P (

i=1

) =

i=1

P (A

) −

P (A

)

P (A

) + ···+ (−1)

n−1

P (A

. . . A

). (1.4)

8 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

The formula (1.4) gives probability of the sum of any number of events through

probabilities of products of these events.

Using the formula (1.3) it is possible to express the probability of the product

of two events through probabilities of individual events and the probability of the

sum of events

P (A

) = P (A

) + P (A

) − P (A

+ A

). (1.5)

The general formula for an arbitrary number of events n looks like

P (A

. . . A

) =

P (A

) −

P (A

+ A

)

P (A

+ A

)

+ ··· + (−1)

n−1

P (A

+ ··· + A

). (1.6)

The formulae (1.4) and (1.6) can be used at transformation of various expressions

containing the sums and products of events.

Example 1.7. The electronic device contains two doubling elements A

and A

and one element C, which is not doubled. The event B, consisting in failure of the

electronic device, corresponds to a situation, when the elements A

and A

or C

are under failure:

B = A

+ C,

where A

is failure of the element A

, A

is failure of the element A

and C is

failure of the element C. It is necessary to express probability of the event C

through the probabilities of events containing only the sums, instead of product of

the elementary events A

, A

and C. Using the formula (1.3) we have

P (B) = P (A

) + P (C) − P (A

C). (1.7)

From the formula (1.5) follows

P (A

) = P (A

) + P (A

) − P (A

+ A

). (1.8)

Further, using the formula (1.6) for three events, we have

P (A

C) = P (A

) + P (A

) + P (C) − P (A

+ A

)

− P (A

+ C) − P (A

+ C) + P (A

+ A

+ C). (1.9)

Substituting formulae (1.8) and (1.9) in equality (1.7), we obtain

P (B) = P (A

+ C) + P (A

+ C) − P (A

+ A

+ C).

Basic concepts of the probability theory 9

1.2.2 Nonindependent and independent events

An event A

is called independent from an event A

, if the probability of the event

is independent of occurrence of the event A

Example 1.8. Two coins are ﬂipped. Let consider two events:

• A

is a head falling for the 1-st coin,

• A

is a tail falling for the 2-nd coin.

The probability of event A

does not depend on that, the event A

occur or not.

The event A

is independent of event A

The event A

is called nonindependent from event A

, if the probability of the event

varies in depending on that, the event A

occur or not.

Example 1.9. The 5 balls, two white and three black, are placed into a urn. The

experimenters take out from the urn one by one ball. The events are considered:

is occurrence of a white ball in 1-st experimenter, A

is occurrence of a white

ball in 2 experimenters. Before something is known about event A

, the probability

of the event A

is P (A

) = 2/5. If it is known, that the event A

occurs, the the

probability of A

is 1/4. Whence follows, that the event A

depends on event A

The probability of event A

, calculated provided that has occurred other event

, is called conditional probability events A

and is denoted as P (A

). In the

considered example we have: P (A

) = 2/5, P (A

) = 1/4.

The condition of the independence of the event A

from the event A

is possible

to note as

P (A

) = P (A

The probability of the product of two events is equal to the product of the proba-

bility of one of them on conditional probability another provided that the ﬁrst event

is occurred:

P (A

) = P (A

)P (A

), (1.10)

P (A

) = P (A

)P (A

If the event A

does not depend on event A

, then the event A

does not depend

on event A

P (A

) = P (A

P (A

) = P (A

The probability of the product of two independent events is equal to the product

of the probabilities of these events

P (A

) = P (A

)P (A

). (1.11)

10 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

The probability of the product of some events is equal to the product of probabilities

of these events provided that the previous events are occurred,

P (A

. . . A

) = P (A

)P (A

) . . .

. . . P (A

. . . A

n−1

). (1.12)

The probability of product of independent events is equal to product of probabilities

of these events:

P (A

. . . A

) = P (A

)P (A

) . . . P (A

). (1.13)

Example 1.10. The ampliﬁer of seismic station has three basic elements, which

ensure a reliable operation during time t. Probabilities of non-failure operation of

devices: p

= 0.9, p

= 0.8, p

= 0.8. The ampliﬁer fails at a failure of any of

devices. Let’s consider the following events:

• B is on-failure operation of the ampliﬁer,

• A

is on-failure operation of the 1-st element,

• A

is on-failure operation of the 2-nd element,

• A

is on-failure operation of the 3-d element,

B = A

Taking into account that the events are independent, we can write

P (B) = P (A

)P (A

) = 0.9 · 0.8 · 0.8 = 0.576.

1.2.3 The Bayes formula and complete probability

Let’s ﬁnd probability of event A, which can occur with one from a group of incom-

patible events B

, B

, . . . , B

, usually termed as hypotheses:

P (A) =

i=1

P (B

)P (A/B

). (1.14)

Expression (1.14) is termed as the formula of complete probability.

Let’s determine the conditional probability of a hypothesis B

belonging the

complete group of incompatible events B

, B

, . . . , B

, provided that there was an

event A. Let’s consider known the probability of hypotheses P (B

), P (B

), . . . ,

P (B

), which usually are termed as a priori, i.e. given before realization of an

experiment.

Using the theorem of multiplication, we obtain the formula

P (AB

) = P (A)P (B

/A) = P (B

)P (A/B

P (B

/A) =

P (B

)P (A/B

)

P (A)

, i = 1, 2, . . . , n.

Basic concepts of the probability theory 11

Applying the formula of the complete probability (1.14), we write the Bayes formula:

P (B

/A) =

P (B

)P (A/B

)

i=1

P (B

)P (A/B

)

. (1.15)

The probability of P (B

/A) is termed as a posterior probability of a hypothesis B

provided that the event A occurs.

1.2.4 Exercises

(1) To prove, that if the event A entails event B, then P (B) ≥ P (A).

(2) In a box there are 15 geophones, inclusive of 5 highly sensitive. Three geophones

undertake occasionally. To ﬁnd the probability that even if one of taken three

geophones will appear highly sensitive.

(3) The probability of occurrence of a signal reﬂected from horizon A, is equal P

and from horizon B is equal P

. To ﬁnd probability of occurrence even if one

of these signals, if reﬂected signals are independent.

(4) To ﬁnd probability P (A

) by using known probabilities:

P (A

) = P

, P (A

) = P

, P (A

+ A

) = P

(5) Two of three independent channels of seismic station have failure. To ﬁnd the

probability that the ﬁrst and second channels have failure, if the probabilities

of a failure of the ﬁrst, second and third channels are accordingly equal 0,2; 0,4

and 0,3.

(6) The occurrence of a reﬂex signal is equally possible at any moment of time

interval t

− t

= T . The probability of occurrence of a signal (for this time

interval) is equal P . It is known, that at time t < T the signal will not appear.

To ﬁnd probability of occurrence of a signal in the residuary time interval.

(7) At a seismogram in a given time window the signals reﬂected from horizons

A and B are observed. The statistical properties of noise are those, that the

signal from horizon A is distorted on the average with probability 2/5, and

from horizon B with probability 1/5. The analysis of the seismograms of the

neighboring region has shown, that appearance the signal from horizon A is in

the relation 3:7 to the signal from horizon B. To ﬁnd the probabilities

(a) the locked-on signal is generated by the horizon A,

(b) the locked-on signal is generated by the horizon B.

1.3 Distribution Functions

1.3.1 Random variables

Let (Ω, A, P ) are a probability model of some experiment with a ﬁnite number

of outcomes n(Ω) < ∞ and with algebra A of all subsets Ω. Let’s introduce a

12 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

concept of a random variable, subject to measuring in the random experiments.

Any numerical function ξ = ξ(ω), determined on a ﬁnite space of elementary events,

is termed as a discrete random variable.

Example 1.11. Let’s determine the random variable for model with double tossing

of a coin and with space of outcomes

= HH, ω

= HT, ω

= TH, ω

= TT.

To each outcome we shall associate with the numerical characteristic ξ, which de-

termines a number of falling head H:

ξ(ω

) = 2, ξ(ω

) = 1, ξ(ω

) = 0.

Other example of a random variable can be the indicator of some set: A ∈ A

ξ = I

(ω), I

(ω) =



1, ω ∈ A,

0, ω 6∈ A.

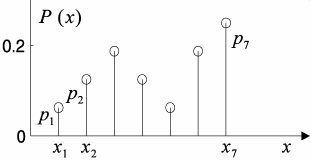
Let’s introduce a distribution of the probability on a range of a random variable.

Since in a considered case Ω consists of a ﬁnite number of points, a range of the

random variable X is also ﬁnite. Let X = {x

, x

, . . . , x

}, where the various

numbers are all values ξ, then

) = P {ω : ξ(ω) = x

}, x

∈ X.

The totality of numbers {P

), . . . , P

)} is termed as a distribution of prob-

abilities of random variable ξ. The example of the graphic representation of the dis-

tribution of probabilities is given at Fig. 1.6. The probability structure of a discrete

Fig. 1.6 Graphic representation of the distribution of probabilities.

random variable is completely described by a distribution function.

1.3.2 Distribution function

If x ∈ R

, the random variable ξ is deﬁned at real axis (−∞, ∞). For the description

of continuous random variable ξ the distribution function is introduced

(x) = P {ω : ξ(ω) ≤ x}.

Sometimes the distribution function is called as a cumulative distribution function.