Troyan V., Kiselev Y. Statistical Methods of Geophysical Data Processing

Подождите немного. Документ загружается.

Basic concepts of the probability theory 43

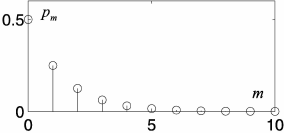
Fig. 1.28 Geometrical distribution (p = 0.5).

• Mathematical expectation Mξ = 1/p.

• Variance Dξ = (1 −p)/p

• Asymmetry coeﬃcient γ

= (2 − p)/(1 − p)

1/2

• Excess γ

= (p

− 6p + 6)/(1 − p).

Example 1.16. During a transmission of an information with the use of the ra-

diochannel there are the noises, which make diﬃculties for decoding the informa-

tion. With the probability p the information fails to be decoded. The information

is transmitted so long as it will not be decoded. The duration of transmission of

the information is equal 2 minutes. To ﬁnd the mathematical expectation of time,

which need for the transmission of the information.

Random variable ξ is a number of “attempts” of the information transmission,

which has a geometrical distribution with T = 2ξ of minutes. The distribution T

can be written as follows:

2 4 6 . . . 2m . . . ,

q pq p

q . . . p

m−1

q . . .

Since m

= 1/p, then M[T ] = 2/p.

1.7.4 Exercises

(1) At seismic stations A and B the seismograms are registered. Let x

is the

event consisting in a signal extraction with the probability p

at a given time

interval on a seismogram A, and x

is the event of a signal extraction with the

probability p

at the station B. It is required to ﬁnd a probability distribution

of a random variable z = x

+ x

, i.e. probability of a signal extraction or at

the station A, or at the station B.

(2) A subunit of a seismic station operates trouble-free during a random time T ,

the subunit renews after a failure. A ﬂow of failures is a stationary one with

the intensity µ. To ﬁnd the probability of events A = {in time τ a subunit it is

not necessary to renews }, B = {the device should be renewed three times }.

(3) The block of a seismic station consists of three subblocks. The ﬁrst subblock

consist of n

elements, the second one consists of n

elements, the third one

consist of n

elements. The ﬁrst subblock is unconditionally necessary for the

operation, second and third duplicate each other. The failure ﬂow is a stationary

44 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

one; for the elements which are included in the ﬁrst subblock, the intensity of

the failure ﬂow is equal λ

, in the second or third subblocks the intensity of the

failure ﬂow is equal λ

. The ﬁrst subblock fails, if not less than two elements

fail. The second (third) subblock fails if even of one element fails. The block of

the seismic station fails if the ﬁrst subblock or second and third subblocks fail

together. To ﬁnd the probability that during a time τ the block of the seismic

station will leave out of the operation.

(4) The artiﬁcial satellite revolving during n of day, may collide randomly with

meteorites. The meteorites are traversing an orbit and colliding with the satel-

lite, form a stationary Poisson ﬂow with intensity κ (meteorites per day). The

meteorite which has hitted the satellite, punches its envelope with the proba-

bility p

. The meteorite, which has punched an envelope, puts out of the action

the devices of the satellite with probability p

. To ﬁnd the probability of the

following events:

(A) — {the envelop is punched during ﬂight time};

(B) — {the devices put out of action during ﬂight time};

during the ﬂight time}.

(5) The hunters are drawn up in a chain by a random fashion so, that they form

on an axis 0x a stationary ﬂow of points with the intensity λ (λ is a number

of the hunters on unity of length). The wolf runs perpendicularly to the chain.

Any hunter shoots at the wolf only in the event that the wolf is distant from it

no greater than R

, and then to hit the mark with the probability p. To ﬁnd

the probability that the wolf will cross the chain, if it does not know, where the

hunters are located and if the chain has a suﬃcient length.

(6) The random events ξ and η are considered which possess the values (0, 1) (pres-

ence and absence of a signal on two recording areas of a seismogram) with a

probability distribution accordingly

ξ :

0 1

and η :

0 1

To draw the probability distributions:

(1) for the sum ζ = ξ + η;

(2) for the diﬀerence ζ = ξ − η;

(3) for the product ζ = ξ ·η.

(7) In a memory cell of a computer n-bit binary number is recorded. Each bit

position of this number, irrespective of the rest of bit positions, has the value

of 0 or 1 with the equal probability. A random variable ξ is a number of bit

positions, which is equal “1”. To ﬁnd the probabilities of the events {ξ = m},

{ξ ≥ m}, {ξ < m}.

(8) On a communication bus k messages are transmitted, which containing n

, n

. . . , n

digits (“0” or “1”). The digits with probability 0.5 are equal to the

Basic concepts of the probability theory 45

values 0 or 1 independent from each other. Each digit is distorted with the

probability p. At coding the messages the error-correcting code in one or two

digits is applied. This code operates practically with a complete reliability. The

presence of an error even in one digit (after correction) leads to the erroneous

message. To ﬁnd probability that even one of k messages will be erroneous.

1.8 Continuous Distributions

If the distribution function F

(x) of random variable ξ for arbitrary x is continuous

and has derivative F

(x), the random variable ξ is called as continuous.

The probability of each value of a continuous random variable is equal to zero.

Probability of the hit ξ in an interval (α, β) is equal to

P (α < ξ ≤ β) = F

(β) − F

(α).

The quantity f

(x)dx in the case of continuous random variable is called an ele-

mentary probability (f

(x) = F

(x) is the density function).

1.8.1 Univariate normal distribution

The random variable ξ has the normal distribution, if its density function reads as

(x) = N(m

, σ

) =

√

2πσ

exp

(

−

(x − m

)

2σ

)

, (1.41)

where m

is the mathematical expectation σ

is the variance of the random variable

ξ. The distribution function of the normal distribution looks as

(x) = Φ



x − m



where

Φ(z) =

√

2π

−∞

exp



−



dy (1.42)

is the Laplace function (Fig. 1.29), which has the next properties:

(1) Φ(−∞) = 0;

(2) Φ(−x) = 1 − Φ(x);

(3) Φ(∞) = 1.

The asymmetry coeﬃcient and excess of the normal distribution are accordingly

equal γ

= 0 and γ

= 0, and the characteristic function is given by the expression

g(t) = exp



itm

−



46 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

Fig. 1.29 The Laplace function and the normal density function. The Laplace function (a):

m = 0, σ = 0.5; The normal density function (b): m

= m

= 0; σ

= 0.5, (1); σ

= 1.0, (2);

= 1.5, (3); The normal density function (c): m

= −1; m

= 0.5; m

= 2; σ

= σ

= 1.

The moments of the normal distribution are written as follows:

(2s)!

, µ

2s+1

= 0 (s ≥ 1).

The density function of the normal or Gaussian distribution N(m, σ

) is the most

important theoretical distribution in the mathematical statistics. The normal dis-

tribution arises, when the variable ξ is formed as a result of a sum of a great number

of independent (or weakly dependent) random addends, which have a comparable

contribution to the sum.

The probability of the hit into a symmetric interval (−l, l) around m

is equal

P (|ξ − m

| < l) = 2Φ





− 1.

Probabilities of the hit into the intervals

P (−1.64 <

ξ − m

< 1.64) = 0.90,

P (−1.96 <

ξ − m

< 1.96) = 0.95,

P (−2.58 <

ξ − m

< 2.58) = 0.99

are used most frequently. Function N(0, 1) is called the standard normal density

function, and

Φ(x) =

√

2π

−∞

exp



−



is called the standard normal distribution function. The functions N(0, 1) and Φ(x)

are tabulated.

If the random variables ξ

, ξ

, . . . , ξ

are independent and have the normal dis-

tribution, their linear combinations have the following properties.

(1) An arbitrary linear combination of the random variables ξ

has a normal distri-

bution. Let us assume, that the mathematical expectations and the variances of

Basic concepts of the probability theory 47

random variables ξ

, ξ

are denoted accordingly as m

, m

and σ

, σ

, then a

and a

are independent normal variables with the characteristic functions

(t) = exp(ita

−

(t) = exp(ita

−

The characteristic function η = a

+ a

is equal

(t) = g

· g

= exp[it(a

+ a

) −

+ a

)],

i.e. η has the normal distribution with the mathematical expectation m

+ a

and the variance σ

= a

+ a

. It is possible to show, that

η =

i=1

have the normal distribution with the mathematical expectation

i=1

and variance σ

i=1

(2) The sample mean

ξ =

i=1

and sample variance

i=1

(ξ

−

ξ)

are independent random variables, if ξ

have an equal normal distributions (with

equal m

and σ

). This is a property of the normal distribution only.

1.8.2 Multivariate normal distribution

System of random variables ξ

, ξ

, . . . , ξ

or n-dimensional vector ξξ = (ξ

, ξ

, . . . , ξ

)

has the normal distribution, if its density function f

(xx) reads as

ξξ

(

x) = (2π)

−n/2

−1/2

exp

−(1/2)(x − m

)

−1

(xx −mm

)

where the mathematical expectation Mξξ = m

and covariance matrix with the

elements [D

]

= M[(ξ

− m

ξi

)(ξ

− m

ξj

)] determine the distribution completely.

The characteristic function is written as follows:

(t) = exp



− (1/2)tt



In case of a two-component random vector the density function looks like

, x

) =

2πσ

√

1 − r

exp

−

2(1 − r

)

− m

)

− 2r

− m

)(x

− m

)

− m

)

, (1.43)

48 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

D =



rσ



, r =

M[(ξ

− m

)(ξ

− m

)]

where r is the correlation coeﬃcient of the random variables ξ

and ξ

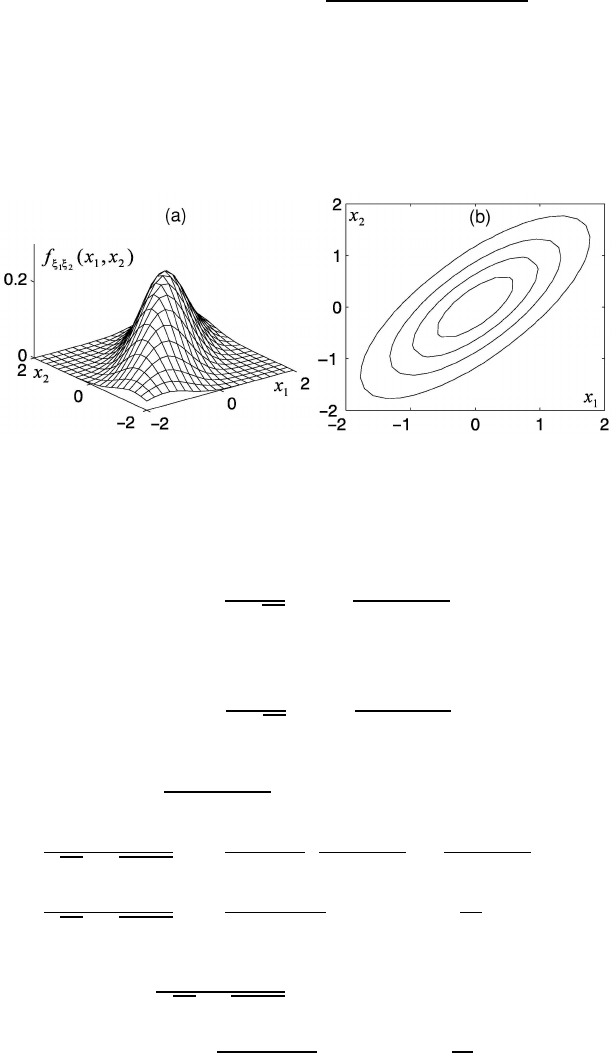
(Fig. 1.30).

To ﬁnd the marginal density function f

) =

∞

−∞

, x

)dx

Fig. 1.30 Two-dimensional normal density function for the random variables ξ

and ξ

: m

= 0; σ

= σ

= 1; r = 0.75: (a) is a three-dimensional representation; (b) is a representation

at the (x

, x

) plane.

To perform an interaction of the density function (1.43), we obtain

√

2π

exp



−

− m

)

2σ



i.e. the variable ξ

has the normal distribution with the mathematical expectation

and the variance σ

. It is similarly possible to show, that

√

2π

exp



−

− m

)

2σ



To ﬁnd conditional density function

/ξ

) =

, x

)

√

2πσ

√

1 − r

exp



−1

2(1 − r

)



− m

)

− r

− m

)





√

2πσ

√

1 − r

exp



−1

2(1 − r

)σ



− m

) − r

− m

)





and, accordingly,

/ξ

) =

√

2πσ

√

1 − r

× exp



−

2(1 − r

)σ



− m

) − r

− m

)





Basic concepts of the probability theory 49

After an analysis of f

/ξ

) we can conclude, that this is a normal distribution

with the mathematical expectation

/ξ

= m

+ r(σ

/σ

)(x

− m

)

and the standard deviation

/ξ

= σ

1 − r

Thus m

/ξ

is called the conditional mathematical expectation, and σ

/ξ

is called

the conditional variance. The dependence m

/ξ

is possible to represent on a plane

as a line, which is called the line of a regression ξ

on ξ

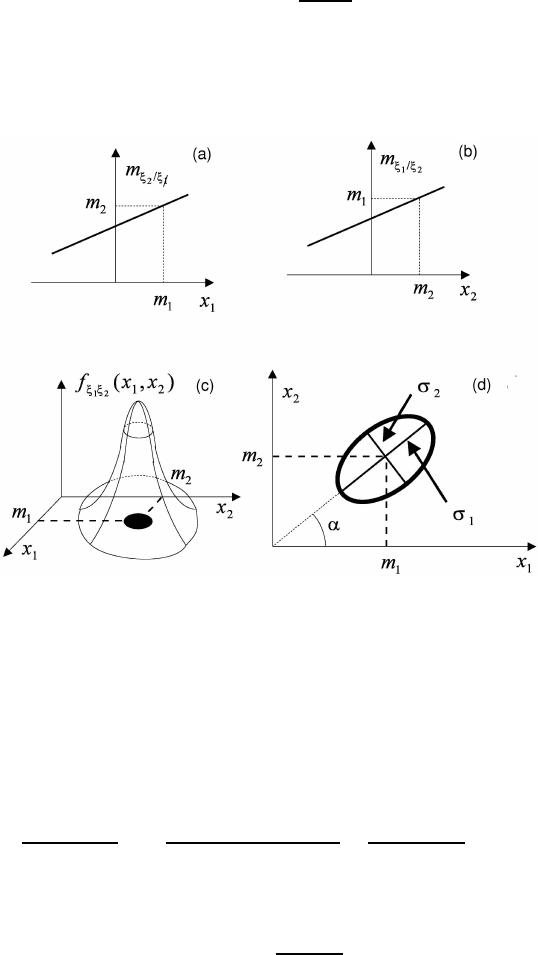
(Fig. 1.31). In the case

Fig. 1.31 Two-dimensional normal distribution: (a) and (b) are conditional mathematical expec-

tations ξ

and ξ

accordingly; (c) is a representation of the density function; (d) is a contour of

the density function at a plane (x

, x

of independent random variables ξ

and ξ

the lines of a regression are parallel

to the coordinate axises. The section of a surface of a bivariate density function

, x

) by the plane, which is parallel to the axis of values f

, x

), gives

curve, similar Gaussian curve. The section of the density function by plane, which

is parallel to the plane x

, gives an ellipse

− m

)

− 2r

− m

)(x

− m

)

− m

)

= λ

The center of the ellipse is in a point with coordinates (m

, m

). A direction of

symmetry axes make with an axis 0x

a corner α:

tan 2α =

2rσ

− σ

50 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

Such ellipse are called the equiprobability ellipse or the ellipse of dispersion (see Fig.

1.31(d)).

Yielding transfer of an origin of coordinates to a point (m

, m

) and rotational

displacement with a corner α, we get a canonical form of an ellipse.

The set of variables, when each of them is a linear function of variables with the

normal distribution, also has the multivariate normal distribution.

Example 1.17. The random point (ξ

, ξ

) has the normal distribution on a plane

with parameters m

= 1, m

= −2, σ

= 1, σ

= 4, r = 0. To ﬁnd a probability

that the random point will hit inside of the area D, which restricted by the ellipse

− 1)

+ 2)

= 1.

To write the density function as

, x

) =

2πσ

exp



−



− 1)

+ 1)



The ellipse of dispersion D

is determined by the formula

− 1)

+ 1)

= k

Let us make a change of variables (x

− 1)/σ

= u

, (x

+ 1)/σ

= u

and we

transform an ellipse D

to a circle c

of the radius k. Then the probability of the

hit can be written as follows:

P ((ξ

, ξ

) ∈ D

) =

2π

exp



−





Let us transfer to the polar frame

= ρ cos θ, u

= ρ sin θ.

The Jacobian of this transformation is equal ρ. After the integration, we obtain

P ((ξ

, ξ

) ∈ D

) =

2π

−π

ρ exp



−



dρdθ

ρ exp



−



dρ = 1 − exp



−



and for the case k = 1 we have

P ((ξ

, ξ

) ∈ D

) = 1 − exp



−



≈ 0.393.

Basic concepts of the probability theory 51

Fig. 1.32 Uniform density function.

1.8.3 Uniform distribution

The random variable ξ has the uniform distribution on the interval from a to b, if

its density function

(x) =



(b − a)

−1

, if x ∈ (a, b),

0, if x 6∈ (a, b)

(1.44)

on this interval is constant (Fig. 1.32).

• Mathematical expectation: Mξ = (a + b)/2.

• Variance: Dξ = (b − a)

/12.

• Asymmetry coeﬃcient: γ

= 0.

• Excess γ

= −1.2.

The typical requirements of origin of the uniform distribution consist in the fol-

lowing: the point M is tossed randomly on an axis 0x, which is divided on equal

intervals of length l. The lengths of random segments ξ

and ξ

, on which the point

M divides an interval (on which it has hitted), has the uniform distribution on the

interval (0, l).

1.8.4 χ

–distribution

The random variable η =

i=1

, which is a sum of random variables having the

standard normal distribution ξ

∈ N (0, 1), have the χ

–distribution with n degrees

of freedom (Fig. 1.33):

(x) =









(x/2)

(n/2)−1

exp(−x/2)



/(2Γ(n/2)), x > 0,

0, x < 0.

(1.45)

The density function f

(x) depends on one parameter n, which is called the number

of degrees of freedom.

• Mathematical expectation: Mξ = n.

• Variance: Dξ = 2n.

• Asymmetry coeﬃcient: γ

= 2

2/n.

52 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

Fig. 1.33 χ

–distribution: 1 — n = 1; 2 — n = 2; 3 — n = 3; 4 — n = 6.

• Excess γ

= 12/n.

The characteristic function of χ

–distribution reads as

g(t) = (1 − 2it)

−n/2

At the limit of n → ∞ the χ

–distribution tends to a normal distribution, and at

n > 30 with an enough good accuracy it is possible to consider this distribution as

the normal one. The χ

–distribution has found wide application in problems of a

test of hypothesis.

If ξ

, ξ

, . . . , ξ

is a sample belongs to the normal distribution N (m, σ

) with

the sample expectation

ξ =

i=1

and the sample variance

n − 1

i=1

(ξ

−

ξ)

then the random variable

η =

(n − 1)s

i=1

(ξ

−

ξ)

∈ χ

n−1

has the χ

-distribution with n − 1 degrees of freedom.

1.8.5 Student’s distribution (t-distribution)

If ξ

, ξ

, . . . , ξ

are the random variables and each of them has the normal distribu-

tion N(m, σ

), then the random variable

η =

√

ξ − m

)

, (1.46)

where

ξ =

i=1

, s

n − 1

i=1

(ξ

− m

)