Troyan V., Kiselev Y. Statistical Methods of Geophysical Data Processing

Подождите немного. Документ загружается.

Basic concepts of the probability theory 13

Fig. 1.7 The graphic representation of the distribution function for a continuous random variable.

The graphic representation of the distribution function is given on Fig. 1.7.

The distribution function is the universal characteristic of the random variable,

it exists both for continuous, and for discrete random variables:

(x) =

{i: x

≤x}

where

) = F

) − F

−

), F

−

) = lim

y→x

(y).

If x

< x

< ··· < x

is carried out and is assumed F

) = 0, then

) = F

) − F

i−1

), i = 1, 2, . . . , n.

An example of graphic representation of the distribution function of the discrete

random variable is given in Fig. 1.8.

Fig. 1.8 Graphic representation of the distribution function of the discrete random variable.

The distribution function has the following properties:

(1) is non-increasing function of its argument x: F (x

) ≥ F (x

), x

> x

;

(2) is equal to zero for x = −∞: F

(−∞) = 0;

(3) is equal to one for x = +∞: F

(+∞) = 1.

14 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

On the basis of the deﬁnition of the distribution function it is possible to conclude,

that the probability of occurrence of the random variable ξ in the given interval

(α, β) is equal an increment of the distribution function on this interval

(α < ξ ≤ β) = F

(β) −F

(α).

1.3.3 The density function

The random variable ξ is called a continuous random variable, if its distribution

function F

(x) is continuous on x. The random variable is called an absolutely

continuous random variable, if there is a non-negative function f

(x), named the

density function, such, that

(x) =

−∞

(y)dy, x ∈ R

The density function is the derivative of the distribution function

(x) = F

(x).

Fig. 1.9 The deﬁnite integral from the density function makes sense of probability.

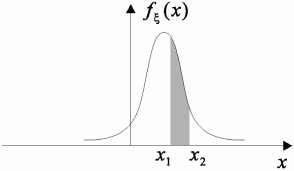
The probability of event α < ξ ≤ β is given by the deﬁnite integral (Fig. 1.9)

P (α < ξ ≤ β) =

(x)dx.

Properties of the density function:

(1) f

(x) ≥ 0;

(2)

∞

−∞

(x)dx = 1.

Basic concepts of the probability theory 15

1.3.4 The distribution and density of function of one random

argument

Let there is a continuous random variable ξ with the density function f

(x), other

random variable η is connected to it by the functional dependence

η = ϕ(ξ).

We shall assume, that the function ϕ is continuous, diﬀerentiable and monotonous

on ξ. For a ﬁnding of the density function of f

(y) it is necessary to ﬁnd function

ψ, which is reciprocal function of ϕ, and also its derivative ψ

, then

(y) = f

(ψ(y))|ψ

(y)|.

If the function ϕ is a nonmonotonic one at the interval (a, b) it can treat as follows

(Fig. 1.10). Let us draw a straight line l, parallel to an axis x, and choose a segment

Fig. 1.10 Construction of the density function in case of nonmonotomic dependence ν = ϕ(ξ).

of a curve y = ϕ(x), on which a condition η < y is satisﬁed. Let us designate these

segments on the abscissa axis as the sites ∆

(y), ∆

(y), . . . , ∆

(y). The event η ≤ y

is equivalent to a hitting of random variable η into one of the sites ∆

(y), ∆

(y), . . . :

(y) = P {ω : η(ω) ≤ y}

= P {ω : (ξ(ω) ∈ ∆

(y) + ξ(ω) ∈ ∆

(y) + . . . )}

P {ω : ξ(ω) ∈ ∆

(y)}.

Example 1.12. To ﬁnd the law of the distribution of a linear function from a

random argument, which has the normal law:

ξ ∈ N(m

, σ

), f

(x) =

exp



−

(x−m

)

2σ



√

2πσ

where η = a

+ a

ξ and a

, a

are nonrandom values. By deﬁnition we have

(y) = f

(ψ(y))|ψ

(y)|, whence follows, that ψ(y) = (y −a

)/a

, |ψ

(y)| = 1/|a

and it is the normal law of distribution with the parameters m

= a

+ a

= |a

|σ

(y) =

|σ

√

2π

exp

−

[y − (a

+ a

)]

2|a

The linear function from a random variable, which distributed under the normal

law is distributed also under the normal law.

16 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

1.3.5 Random vectors

In practice there is a necessity along with the random variable to consider the

random vector

ξ = (ξ

, . . . , ξ

), which components are random variables. A set of

probabilities

, . . . , x

) = P {ω : ξ

(ω) = x

, . . . , ξ

(ω) = x

where x

∈ X

are admitted regions of ξ

, is called a probability distribution of the

random vector ξ. The function

, . . . , x

) = P {ω : ξ

(ω) ≤ x

, . . . , ξ

(ω) ≤ x

}

is called a distribution function of the random vector

ξ. In the applied literature

on the theory of probabilities the components of a random vector is named as a

system of random variables or geometrical interpretation of a random point with

coordinates appropriate to components of a vector is used. In the case, when the

vector

ξ has two components (ξ, η), the distribution function looks like

ξη

(x, y) = P {ω : ξ(ω) ≤ x, η(ω) ≤ y}.

Let us consider the properties of the distribution function for two random vari-

ables.

(1) F

ξη

(x, y) is non-increasing function of its arguments, i. e.

(1) if x

> x

, F

ξη

, y) ≥ F

ξη

, y),

(2) if y

> y

, F

ξη

(x, y

) ≥ F

ξη

(x, y

(2) At equality of one or both arguments to a minus of inﬁnity, the distribution

function is equal to zero:

ξη

(x, −∞) = F

ξη

(−∞, y) = F

ξη

(−∞, −∞) = 0.

(3) At equality of one of arguments to a plus of inﬁnity the distribution function

of a system of random variables turns to the distribution function of a random

variable appropriate to one argument, i. e.

ξη

(x, +∞) = F

(x), F

ξη

(+∞, y) = F

(y).

(4) At equality of both arguments to a plus of inﬁnity, the distribution function is

equal 1:

ξη

(+∞, +∞) = 1.

Density function of a random vector, containing two components, we shall name

the density function of two variables

ξη

(x, y) =

∂

ξη

(x, y)

∂x∂y

Basic concepts of the probability theory 17

It is possible to write down a probability of an occurrence into a rectangular D,

limited by abscissas α and β and ordinates γ and δ, as an integral of the density

function

P {ω : (ξ(ω), η(ω)) ∈ D} =

ξη

(x, y)dxdy.

The distribution function is expressed through the density function as follows:

ξη

(x, y) =

−∞

ξη

(x, y)dxdy.

1.3.6 Marginal and conditional distributions

Having the law of the distribution of two random variables or the random vector

with two components, it is possible to receive the law of the distribution of one of

random variables

(x) = F

ξη

(x, ∞), F

(y) = F

ξη

(∞, y).

Let us represent them through the density function:

(x) =

−∞

∞

−∞

f(x, y)dxdy, (1.16)

(y) =

∞

−∞

f(x, y)dxdy. (1.17)

If we diﬀerentiate (1.16) on x and (1.17) on y, we can write

(x) = F

(x) =

∞

−∞

f(x, y)dy, f

(y) = F

(y) =

∞

−∞

f(x, y)dx.

The density functions f

(x) and f

(y), received by integration in inﬁnite limits of

two-dimensional density function f

ξη

(x, y) on variables y and x correspondingly, are

called as a marginal density function or marginal densities. A conditional density

function or a conditional density is determined as

ξ/η

(x/y) =

ξη

(x, y)

(y)

ξη

(x, y)

∞

−∞

ξη

(x, y)dx

η/ξ

(y/x) =

ξη

(x, y)

(x)

ξη

(x, y)

∞

−∞

ξη

(x, y)dy

18 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

A joint density function or a joint density can be written down using conditional

and marginal densities:

ξη

(x, y) = f

(y)f

ξ/η

(x/y), (1.18)

ξη

(x, y) = f

(x)f

η/ξ

(y/x). (1.19)

The conditional density f

ξη

(x/y

) can be represented as a section of two-dimensional

density f

ξη

(x, y) by a vertical plane, which is orthogonal to the axis y and crosses

a point y = y

(Fig. 1.11). The components ξ and η of a random vector are called

Fig. 1.11 Graphic representation of joint (a) and conditional density functions (b).

independent random variables, if

ξ/η

(x/y) = f

(x) and f

η/ξ

(y/x) = f

(y),

i. e. conditional densities are equal to the marginal ones. For independent random

variables the next equality is valid

ξη

(x, y) = f

(x)f

(y).

Using the formulae (1.18) and (1.19), it is possible to get an analog of the Bayes

formula for continuous random variable

ξ/η

(x/y) =

(x)f

η/ξ

(y/x)

∞

−∞

ξη

(x, y)dx

. (1.20)

This formula will be used further for a ﬁnding the estimations of parameters by the

Bayes criterion.

1.3.7 The distributive law of two random variables

Let there is a system of two continuous random variables (ξ, η) with the density

function f

ξη

(x, y). The random variable ζ is connected with ξ and η by the func-

tional dependence

ζ = ϕ(ξ, η).

Basic concepts of the probability theory 19

Fig. 1.12 Geometrical illustration to a development of the distributive law of the function of two

random arguments.

Let us ﬁnd the distributive law of ζ. We use geometrical interpretation for an

obtaining the distributive law of ζ

(z) = P {ω : ζ(ω) < z} = P {ω : ϕ(ξ(ω), η(ω)) < z},

which is represented at Fig. 1.12. Let us to pass a plane Q in parallels to a plane

x0y on distance z from it. Let us express as D an area on a plane x0y, which is

satisﬁed condition ϕ(ξ, η) < z. Then

(z) = P {ω : (ξ, η) ∈ D} =

D(z)

ξη

(x, y)dxdy.

As an example we shall ﬁnd the distributive law of the sum of two random

variables ζ = ξ +η. On the plane x0y we pass a line given by the equation z = x+y.

This straight line divides a plane into two parts: more to the right and above

ξ + η > z, more to the left and below ξ + η < z — (Fig. 1.13). Domain D in our

Fig. 1.13 Domain of integration on the plane (x, y).

case is shaded the left and bottom part of a plane. Let us represent the distribution

20 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

function F

(z) as integral of density function f

ξη

(x, y):

(z) =

D(z)

ξη

(x, y)dxdy =

∞

−∞

z−x

−∞

ξη

(x, y)dxdy

∞

−∞







z−x

−∞

ξη

(x, y)dy







dx.

Diﬀerentiating this expression on z (upper limit of integration of inner integral), we

shall get an expression for the density function

(z) =

∞

−∞

ξη

(x, z − x)dx, (1.21)

or, starting from a symmetry of the task,

(z) =

∞

−∞

ξη

(z − y, y)dy. (1.22)

If the random variables ξ and η are independent, the distributive law of the sum of

these variables is represented by a composition of distributive laws:

ξη

(x, y) = f

(x)f

(y),

and formulae (1.21), (1.22) can be written in the following form:

(z) =

∞

−∞

(x)f

(z − x)dx,

(z) =

∞

−∞

(z − y)f

(y)dy.

Using denotation ∗ (convolution), we get f

(z) = f

∗ f

Example 1.13. Consider composition of the normal laws:

ξ ∈ N(m

, σ

), f

(x) =

√

2π

exp



−

(x − m

)

2σ



η ∈ N(m

, σ

), f

(y) =

√

2π

exp



−

(y − m

)

2σ



and to ﬁnd the distributive law of

ζ = ξ + η.

Basic concepts of the probability theory 21

Let us apply the convolution formula for a composition:

g(z) =

∞

−∞

(x)f

(z − x)dx

2πσ

∞

−∞

exp



−

(x − m

)

2σ

−

(z − x − m

)

2σ



dx.

Uncovering brackets in an exponent of an exponential curve, we get

g(z) =

2πσ

∞

(−∞)

exp(−a

+ 2a

x − a

)dx,

+ σ

, a

2σ

z − m

2σ

(z − m

)

2σ

Using a standard integral

∞

−∞

exp(−a

+ 2a

x − a

)dx =

exp



−

− a



we obtain after transformations

g(z) =

√

2π

+ σ

exp



−

[z − (m

+ m

)]

2(σ

+ σ

)



It is the normal law with the mathematical expectation m

= = m

+ m

and with

the variance σ

= σ

+ σ

1.3.8 Exercises

(1) The random variable ξ obeys the Cauchy distribution with the density function

(x) =

π(1 + x

)

The variable η is interlinked with ξ by the relation

η = 1 − ξ

To ﬁnd a density function of the random variable η.

(2) The random variable ξ obeys the uniform law with the density function on a

line segment (−π/2, π/2):



1/π, if |x| < π/2,

0, if |x| > π/2.

To ﬁnd a distributive law of η = cos ξ.

22 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

(3) A random variable ξ obeys the normal law

ξ ∈ N(m

, σ

), f

(x) =

√

2πσ

exp

(

(x − m

)

2σ

)

and a random variable η has the uniform density function

(y) =

β − α

if α < y < β.

To ﬁnd a density function of ζ = η + ξ.

(4) The random variable ξ has the uniform law on a line segment

(x) =



1/π, if x ∈ (−π/2, π/2),

0, if x 6∈ (−π/2, π/2).

To ﬁnd a density function of η = sin ξ.

(5) The random variable ξ obeys the Rayleigh law with the density function

(x) =

exp



−

2σ



if x > 0.

To ﬁnd the density function of η = e

−ξ

(6) At interpretation of the geophysical data frequently there is a necessity of the

deﬁnition of a distributive law of a random variable η provided that the random

variable ξ = ln η has the normal distribution with the parameters m

and σ

To ﬁnd the density function of a random variable η.

(7) The system of the random variables (ξ, η) obeys the distributive law with the

density function f

ξη

(x, y). To ﬁnd a density function f

(z) for the random vari-

able ζ = ξη.

I n s t r u c t i o n . We ﬁx some value z, then on a plane x0y we build a curve

with an equation z = xy. It is a hyperbola. Distribution function is given by

the formula

(z) = P ((ξ, η) ∈ D) = P (ξη < z), f

(z) = G

(z).

(8) The system of random variables (ξ, η) has a joint density function f

ξη

(x, y). To

ﬁnd the density function f

(z) of their ratio ζ = η/ξ.

(9) To ﬁnd a distributive law ζ = η/ξ of two independent normally distributed

variables ξ, η with parameters m

= m

= 0, σ

, σ

(10) To ﬁnd a distributive law of a random variable ζ = ξ + η, if ξ and η are

independent random variables, which obey the exponential law with density

functions

(x) = λe

−λx

(x > 0), f

(y) = µe

−µy

(y > 0).