Trauth M.H., MATLAB® Recipes for Earth Sciences, Third edition
Подождите немного. Документ загружается.

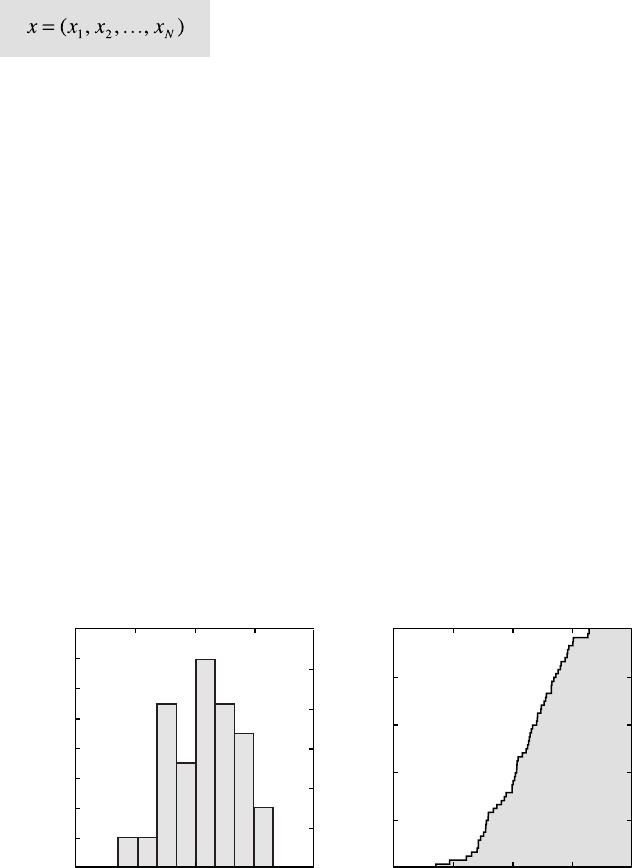
38 3 UNIVARIATE STATISTICS
x-Value x-Value
Cumulative Frequency
Frequency
Histogram Cumulative Histogram
ab
8 10121416
0
2
4
6
8
10
12
14
16
8 10121416
0
0.2
0.4
0.6
0.8
1.0
Fig. 3.1 Graphical representation of an empirical frequency distribution. a In a histogram,
the frequencies are organized in classes and plotted as a bar plot. b e cumulative histogram
of a frequency distribution displays the totals of all classes lower than and equal to a certain
value. e cumulative histogram is normalized to a total number of observations of one.
tion of interest, can be written as a vector x
containing a total of N observations. e vector x may contain a large num-
ber of data points, and it may consequently be di cult to understand its
properties. Descriptive statistics are therefore o en used to summarize the
characteristics of the data. e statistical properties of the data set may be
used to de ne an empirical distribution, which can then be compared to a
theoretical one.
e most straightforward way of investigating the sample characteris-
tics is to display the data in a graphical form. Plotting all of the data points
along a single axis does not reveal a great deal of information about the data
set. However, the density of the points along the scale does provide some
information about the characteristics of the data. A widely-used graphi-
cal display of univariate data is the histogram (Fig. 3.1). A histogram is a
bar plot of a frequency distribution that is organized in intervals or classes.
Such histogram plots provide valuable information on the characteristics
of the data, such as the central tendency, the dispersion and the general
shape of the distribution. However, quantitative measures provide a more
accurate way of describing the data set than the graphical form. In purely
3.2 EMPIRICAL DISTRIBUTIONS 39
3 UNIVARIATE STATISTICS
Median
Mean Mode
Outlier
Median
Mean Mode
8 10121416
0
5
10
15
02468
0
10
20
30
40
50
x-Value x-Value
Frequency
Frequency
Skew Distribution
Symmetric Distribution
ab
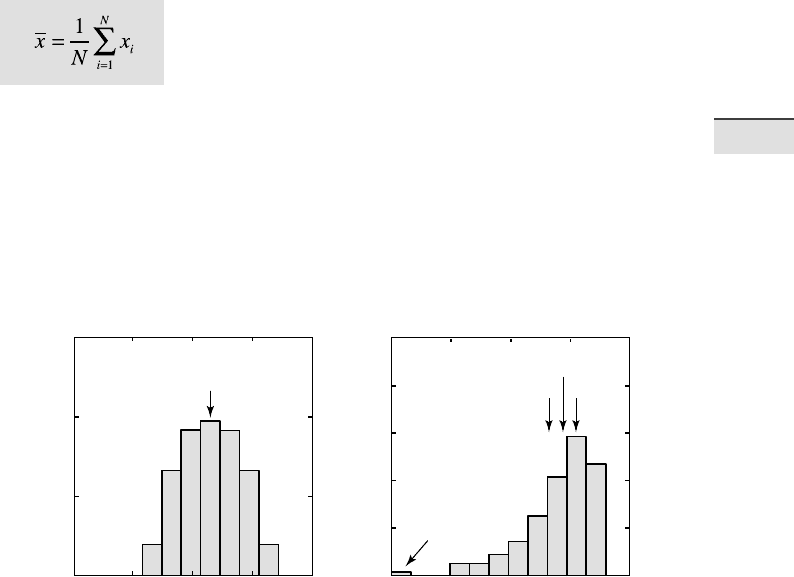
Fig. 3.2 Measures of central tendency. a In an unimodal symmetric distribution, the mean,
the median and the mode are identical. b In a skewed distribution, the median lies between
the mean and the mode. e mean is highly sensitive to outliers, whereas the median and
the mode are little in uenced by extremely high and low values.
quantitative terms, the mean and the median de ne the central tendency of
the data set, while the data dispersion is expressed in terms of the range and
the standard deviation.
Measures of Central Tendency
Parameters of central tendency or location represent the most important
measures for characterizing an empirical distribution (Fig. 3.2). ese val-
ues help locate the data on a linear scale. ey represent a typical or best
value that describes the data. e most popular indicator of central ten-
dency is the arithmetic mean, which is the sum of all data points divided by
the number of observations:
e arithmetic mean can also be called the mean or the average of a uni-
variate data set. e sample mean is used as an estimate of the population
mean μ for the underlying theoretical distribution. e arithmetic mean is,
however, sensitive to outliers, i. e., extreme values that may be very di erent
from the majority of the data, and the median is therefore o en used as an

40 3 UNIVARIATE STATISTICS
alternative measure of central tendency. e median is the x-value that is in
the middle of the data set, i. e., 50 % of the observations are larger than the
median and 50 % are smaller. e median of a data set sorted in ascending
order is de ned as
if N is odd and
if N is even. Although outliers also a ect the median, their absolute values
do not in uence it. Quantiles are a more general way of dividing the data
sample into groups containing equal numbers of observations. For example,
the three quartiles divide the data into four groups, the four quintiles di-
vide the observations in ve groups and the 99 percentiles de ne one hun-
dred groups.
e third important measure for central tendency is the mode. e
mode is the most frequent x value or – if the data are grouped in classes –
the center of the class with the largest number of observations. e data set
has no mode if there are no values that appear more frequently than any of
the other values. Frequency distributions with a single mode are called uni-
modal, but there may also be two modes ( bimodal), three modes ( trimodal)
or four or more modes ( multimodal).
e mean, median and mode are used when several quantities add to-
gether to produce a total, whereas the geometric mean is o en used if these
quantities are multiplied. Let us assume that the population of an organism
increases by 10 % in the rst year, 25 % in the second year, and then 60 % in
the last year. e average rate of increase is not the arithmetic mean, since
the original number of individuals has increased by a factor (not a sum)
of 1.10 a er one year, 1.375 a er two years, or 2.20 a er three years. e
average growth of the population is therefore calculated by the geometric
mean:
e average growth of these values is 1.4929 suggesting an approximate per
annum growth in the population of 49 %. e arithmetic mean would result
in an erroneous value of 1.5583 or approximately 56 % annual growth. e
geometric mean is also a useful measure of central tendency for skewed or
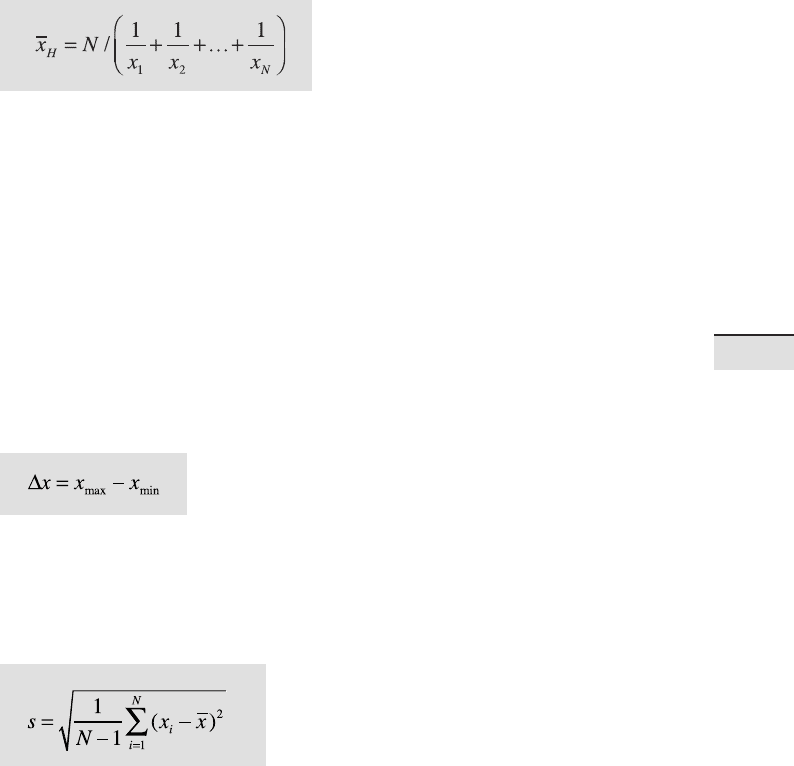
3.2 EMPIRICAL DISTRIBUTIONS 41
3 UNIVARIATE STATISTICS
log-normally distributed data, in which the logarithms of the observations
follow a Gaussian or normal distribution. e geometric mean, however,
is not used for data sets containing negative values. Finally, the harmonic
mean
is also used to derive a mean value for asymmetric or log-normally distrib-
uted data, as is the geometric mean, but neither is robust to outliers. e
harmonic mean is a better average when the numbers are de ned in relation
to a particular unit. e commonly quoted example is for averaging veloci-
ties. e harmonic mean is also used to calculate the mean of sample sizes.
Measures of Dispersion
Another important property of a distribution is the dispersion. Some of
the parameters that can be used to quantify dispersion are illustrated in
Figure 3.3. e simplest way to describe the dispersion of a data set is by the
range, which is the di erence between the highest and lowest value in the
data set, given by
Since the range is de ned by the two extreme data points, it is very suscep-
tible to outliers, and hence it is not a reliable measure of dispersion in most
cases. Using the interquartile range of the data, i. e., the middle 50 % of the
data attempts to overcome this problem.
A more useful measure for dispersion is the standard deviation.
e standard deviation is the average deviation of each data point from the
mean. e standard deviation of an empirical distribution is o en used as
an estimate of the population standard deviation σ. e formula for the
population standard deviation uses N instead of N–1 as the denominator.
e sample standard deviation s is computed with N–1 instead of N since it
uses the sample mean instead of the unknown population mean. e sample
mean, however, is computed from the data x
i
, which reduces the number of

42 3 UNIVARIATE STATISTICS
Mode 1 Mode 2
Mode 1
Mode 2
Mode 3
−2 02468 −202468
681012141618
0
5
10
15
20
25
30
35
40
0
5
10
15
20
25
30
35
40
0
20
40
60
80
100
0
10
20
30
40
50
60
70
80
10
20
30
40
50
60
70
80
10
20
30
40
50
60
0
0
Frequency
Frequency
Frequency
Frequency
Frequency
Frequency
x-Value x-Value
x-Value x-Value
x-Value x-Value
0102030
0102030
0102030
Positive SkewnessNegative Skewness
High Kurtosis Low Kurtosis
Bimodal Distribution Trimodal Distribution
a
c
ef
d
b
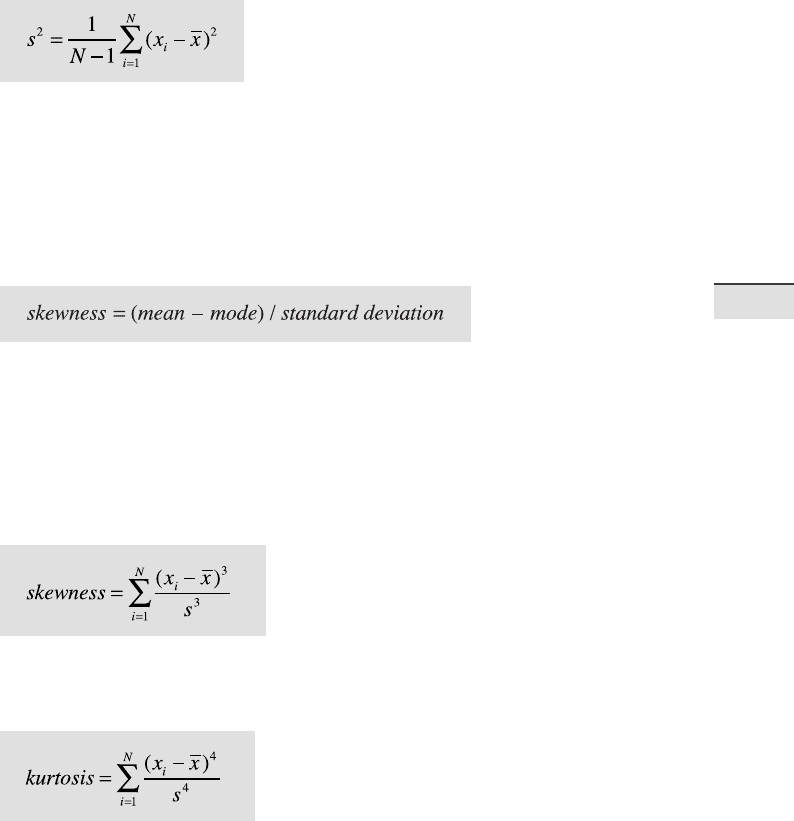
Fig. 3.3 Dispersion and shape of a distribution. a-b Unimodal distributions showing a
negative or positive skew. c-d Distributions showing a high or low kurtosis. e-f Bimodal
and trimodal distributions showing two or three modes.
3.2 EMPIRICAL DISTRIBUTIONS 43
3 UNIVARIATE STATISTICS
degrees of freedom by one. e degrees of freedom are the number of values
in a distribution that are free to be varied. Dividing the average deviation of
the data from the mean by N would therefore underestimate the population
standard deviation σ.
e variance is the third important measure of dispersion. e variance
is simply the square of the standard deviation.
Although the variance has the disadvantage of not having the same dimen-
sions as the original data, it is extensively used in many applications instead
of the standard deviation.
In addition, both skewness and kurtosis can be used to describe the
shape of a frequency distribution. Skewness is a measure of the asymmetry
of the tails of a distribution. e most popular way to compute the asym-
metry of a distribution is by Pearson’s mode skewness:
A negative skew indicates that the distribution is spread out more to the le
of the mean value, assuming values increasing towards the right along the
axis. e sample mean is in this case smaller than the mode. Distributions
with positive skewness have large tails that extend towards the right. e
skewness of the symmetric normal distribution is zero. Although Pearson’s
measure is a useful one, the following formula by Fisher for calculating the
skewness is o en used instead, including in the relevant MATLAB function.
e second important measure for the shape of a distribution is the kurtosis.
Again, numerous formulas to compute the kurtosis are available. MATLAB
uses the following formula:
e kurtosis is a measure of whether the data are peaked or at relative to
a normal distribution. A high kurtosis indicates that the distribution has a
distinct peak near the mean, whereas a distribution characterized by a low
44 3 UNIVARIATE STATISTICS
kurtosis shows a at top near the mean and broad tails. Higher peakedness in
a distribution results from rare extreme deviations, whereas a low kurtosis is
caused by frequent moderate deviations. A normal distribution has a kurtosis
of three, and some de nitions of kurtosis therefore subtract three from the
above term in order to set the kurtosis of the normal distribution to zero.
Having de ned the most important parameters used to describe an em-
pirical distribution, the measures of central tendency and dispersion are
now illustrated by examples.
3.3 Example of Empirical Distributions
As an example, we can analyze the data contained in the le organicmat-
ter_one.txt. is le contains the organic matter content of lake sediments
in weight percentage (wt %). In order to load the data, we type
clear
corg = load('organicmatter_one.txt');
e data le contains 60 measurements that can be displayed by
plot(corg,zeros(1,length(corg)),'o')
is graph shows some of the characteristics of the data. e organic carbon
content of the samples ranges between 9 and 15 wt %, with most of the data
clustering between 12 and 13 wt %. Values below 10 and above 14 are rare.
While this kind of representation of the data undoubtedly has its advantages,
histograms are a much more convenient way to display univariate data.
hist(corg)
By default, the function hist divides the range of the data into ten equal
intervals, bins or classes, counts the number of observations within each
interval and displays the frequency distribution as a bar plot. e midpoints
of the default intervals
v and the number of observations per interval n can
be accessed using
[n,v] = hist(corg)
n =
Columns 1 through 8
2 1 5 8 5 10 10 9

3.3 EXAMPLE OF EMPIRICAL DISTRIBUTIONS 45
3 UNIVARIATE STATISTICS
Columns 9 through 10
8 2
v =
Columns 1 through 5
9.6740 10.1885 10.7029 11.2174 11.7319
Columns 6 through 10
12.2463 12.7608 13.2753 13.7898 14.3042
e number of classes should not be lower than six or higher than een for
practical purposes. In practice, the square root of the number of observa-
tions, rounded to the nearest integer, is o en used as the number of classes.
In our example, we use eight classes instead of the default ten classes.
hist(corg,8)
We can even de ne the midpoint values of the histogram classes. Here, it
is recommended to choose interval endpoints that avoid data points fall-
ing between two intervals. We can use the minimum, the maximum and
the range of the data to de ne the midpoints of the classes. We can then
add half of the interval width to the lowest value in
corg to calculate the
midpoint of the lowest class. e midpoint of the highest class is the highest
value in
corg reduced by half of the interval width.
min(corg) + 0.5*range(corg)/8
ans =
9.7383
max(corg) - 0.5*range(corg)/8
ans =
14.2399
range(corg)/8
ans =
0.6431
We can now round these values and de ne
v = 9.75 : 0.65 : 14.30;
as midpoints of the histogram intervals. is method for de ning the mid-
points is equivalent to the one used by the function
hist if v is not speci-
ed by the user. e commands for displaying the histogram and calculat-
ing the frequency distribution are
hist(corg,v)
46 3 UNIVARIATE STATISTICS
n = hist(corg,v)
n =
2 2 11 7 14 11 9 4
e most important parameters describing the distribution are the mea-
sures for central tendency and the dispersion about the average. e most
popular measure for central tendency is the arithmetic mean.
mean(corg)
ans =
12.3448
Since this measure is very susceptible to outliers, we can take the median as
an alternative measure of central tendency,
median(corg)
ans =
12.4712
which does not di er by very much in this particular example. However, we
will see later that this di erence can be signi cant for distributions that are
not symmetric. A more general parameter to de ne fractions of the data
less than, or equal to, a certain value is the quantile. Some of the quantiles
have special names, such as the three quartiles dividing the distribution
into four equal parts, 0–25 %, 25–50 %, 50–75 % and 75–100 % of the total
number of observations. We use the function
quantile to compute the
three quartiles.
quantile(corg,[.25 .50 .75])
ans =
11.4054 12.4712 13.2965
Less than 25 % of the data values are therefore lower than 11.4054, 25 %
are between 11.4054 and 12.4712, another 25 % are between 12.4712 and
13.2965, and the remaining 25 % are higher than 13.2965.
e third parameter in this context is the mode, which is the midpoint
of the interval with the highest frequency. e MATLAB function
mode to
identify the most frequent value in a sample is unlikely to provide a good
estimate of the peak in continuous probability distributions, such as the
one in
corg. Furthermore, the mode function is not suitable for nding
peaks in distributions that have multiple modes. In these cases, it is better

3.3 EXAMPLE OF EMPIRICAL DISTRIBUTIONS 47
3 UNIVARIATE STATISTICS
to compute a histogram and calculate the peak of that histogram. We can
use the function
find to locate the class that has the largest number of
observations.
v(find(n == max(n)))
or simply
v(n == max(n))
ans =
12.3500
Both statements are identical and identify the largest element in n. e in-
dex of this element is then used to display the midpoint of the correspond-
ing class
v. If there are several elements in n with similar values, this state-
ment returns several solutions suggesting that the distribution has several
modes. e median, quartiles, minimum and maximum of a data set can be
summarized and displayed in a box and whisker plot.
boxplot(corg)
e boxes have lines at the lower quartile, the median, and the upper quartile
values. e whiskers are lines extending from each end of the boxes to show
the extent or range of the rest of the data.
e most popular measures for dispersion are range, standard deviation
and variance. We have already used the range to de ne the midpoints of the
classes. e variance is the average of the squared deviations of each num-
ber from the mean of a data set.
var(corg)
ans =
1.3595
e standard deviation is the square root of the variance.
std(corg)
ans =
1.1660
Note that, by default, the functions var and std calculate the sample vari-
ance and sample standard deviation providing an unbiased estimate of the
dispersion of the population. When using
skewness to describe the shape
of the distribution, we observe a slightly negative skew.
