Trauth M.H., MATLAB® Recipes for Earth Sciences, Third edition
Подождите немного. Документ загружается.

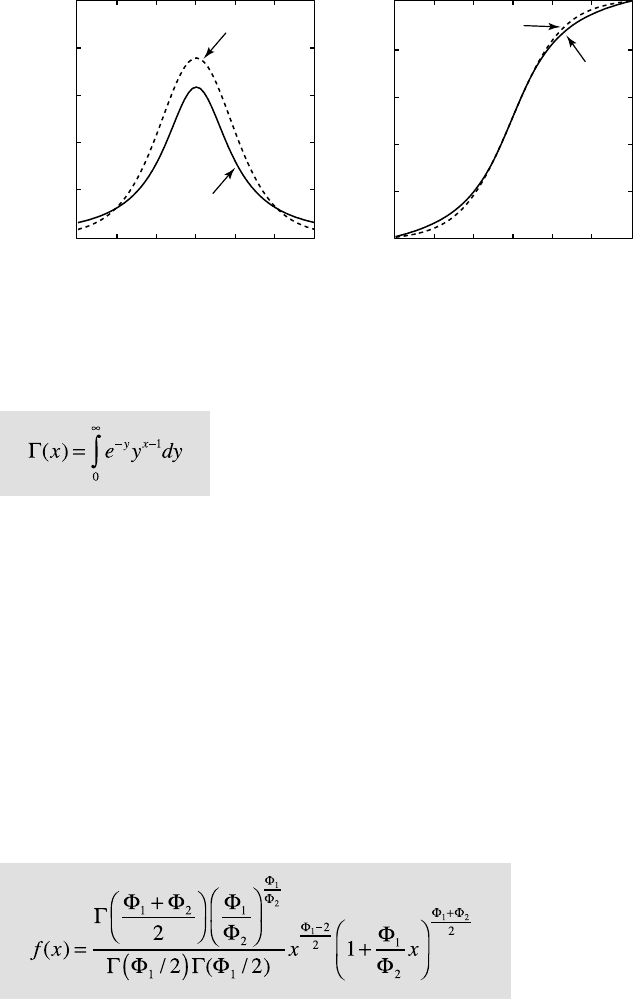
58 3 UNIVARIATE STATISTICS
Φ=5
Φ=5
Φ=1
Φ=1
0.1
0.2
0.3
0.4
−6 −4 −2 0 2 4 6−6 −4 −2 0 2 4 6
0.5
0
0.2
0.4
0.6
0.8
1
0
xx
f(x)
F(x)
Probability Density
Function
Cumulative Distribution
Function
ab
Fig. 3.9 a Probability density function f(x) and b cumulative distribution function F(x) of
a Student's t distribution with two di erent values for Φ.
if x>0. e single parameter Φ of the t distribution is the number of degrees
of freedom. In the analysis of univariate data, this distribution has n–1 de-
grees of freedom, where n is the sample size. As Φ→∞ , the t distribution
converges towards the standard normal distribution. Since the t distribu-
tion approaches the normal distribution for Φ>30, it is rarely used for dis-
tribution tting. However, the t distribution is used for hypothesis testing
using the t-test (Section 3.6).
Fisher’s F Distribution
e F distribution was named a er the statistician Sir Ronald Fisher (1890–
1962). It is used for hypothesis testing using the F-test (Section 3.7). e F dis-
tribution has a relatively complex probability density function (Fig. 3.10):
3.5 EXAMPLE OF THEORETICAL DISTRIBUTIONS 59
3 UNIVARIATE STATISTICS
Φ
1
=1, Φ
2
=5
Φ
1
=10, Φ
2
=10
Φ
1
=1, Φ
2
=5
Φ
1
=10, Φ
2
=10
0.2
0.4
0.6
0.8
0.2
0.4
0.6
0.8
11
00
01234 01234
xx
f(x)
F(x)
Probability Density
Function
Cumulative Distribution
Function
ab
Fig. 3.10 a Probability density function f(x) and b cumulative distribution function F(x) of
a Fisher’s F distribution with di erent values for Φ
1
and Φ
2
.
where x>0 and Γ is again the Gamma function. e two parameters Φ
1
and
Φ
2
are the numbers of degrees of freedom.
χ
2
or Chi-Squared Distribution
e χ
2
distribution was introduced by Friedrich Helmert (1876) and Karl
Pearson (1900). It is not used for tting a distribution, but has important
applications in statistical hypothesis testing using the χ
2
-test (Section 3.8).
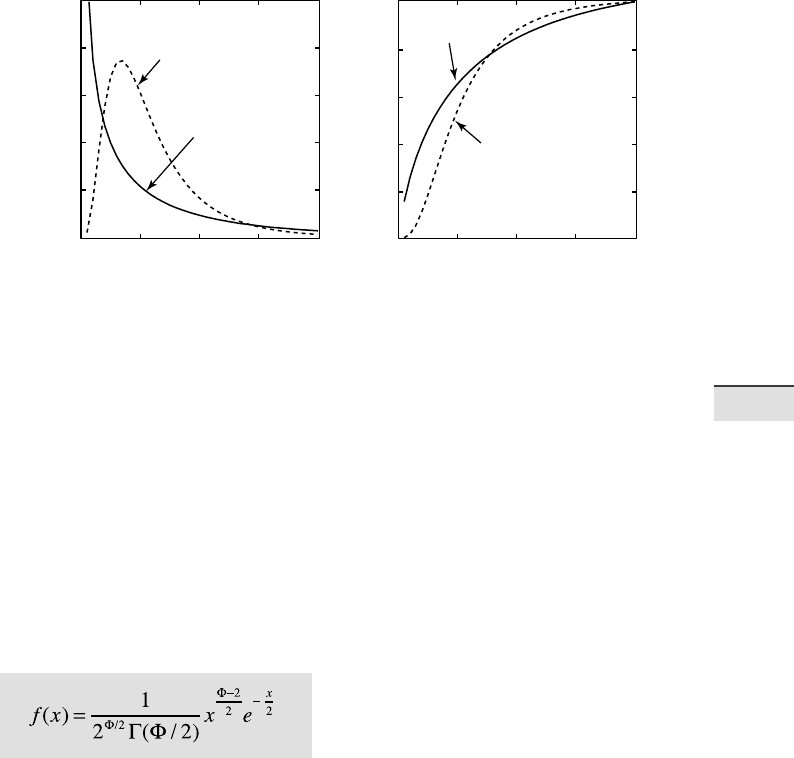
e probability density function of the χ
2
distribution is
where x>0, otherwise f(x)=0; Γ is again the Gamma function. Once again,
Φ is the number of degrees of freedom (Fig. 3.11).
3.5 Example of Theoretical Distributions
e function randtool is a tool to simulate discrete data with statistics sim-
ilar to our data. is function creates a histogram of random numbers from
the distributions in the Statistics Toolbox. e random numbers that have
60 3 UNIVARIATE STATISTICS
Φ =3
Φ =2
Φ =4
Φ =1
Φ =1
Φ =2
Φ =4
Φ =3
0.1
0.2
0.3
0.4
0.2
0.4
0.6
0.8
1
00
02468 02468
0.5
xx
f(x)
F(x)
Probability Density
Function
Cumulative Distribution
Function
ab
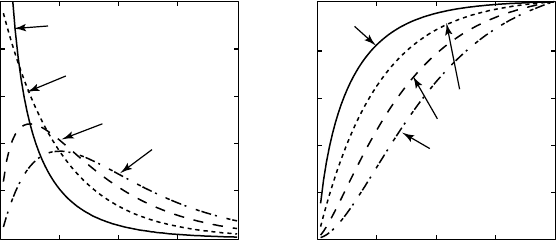
Fig. 3.11 a Probability density function f(x) and b cumulative distribution function F(x) of
a χ
2
distribution with di erent values for Φ.
been generated by using this tool can then be exported into the workspace.
We start the graphical user interface ( GUI) of the function by typing
randtool
a er the prompt. We can now create a data set similar to the one in the le
organicmatter_one.txt. e 60 measurements have a mean of 12.3448 wt %
and a standard deviation of 1.1660 wt %. e GUI uses Mu for μ (the mean
of a population) and Sigma for σ (the standard deviation). A er choosing
Normal for a Gaussian distribution and 60 for the number of samples, we
get a histogram similar to the one in the rst example (Section 3.3). is
synthetic distribution based on 60 samples represents a rough estimate of
the true normal distribution. If we increase the sample size, the histogram
looks much more like a true Gaussian distribution.
Instead of simulating discrete distributions, we can use the probabil-
ity density function (PDF) or cumulative distribution function (CDF) to
compute a theoretical distribution. e MATLAB Help gives an overview
of the available theoretical distributions. As an example, we can use the
functions
normpdf(x,mu,sigma) and normcdf(x,mu,sigma) to
compute the PDF and CDF of a Gaussian distribution with
Mu=12.3448
and
Sigma=1.1660, evaluated for the values in x, to compare the results
with those from our sample data set.

3.6 THE T-TEST 61
3 UNIVARIATE STATISTICS
clear
x = 9 : 0.1 : 15;
pdf = normpdf(x,12.3448,1.1660);
cdf = normcdf(x,12.3448,1.1660);
plot(x,pdf,x,cdf)
MATLAB also provides a GUI-based function for generating PDFs and
CDFs with speci c statistics, which is called
disttool.
disttool
We choose PDF as function type and, then de ne the mean as Mu=12.3448
and the standard deviation as
Sigma=1.1660. Although the function
disttool is GUI-based, it uses the non-GUI functions for calculating
probability density functions and cumulative distribution functions, such
as
normpdf and normcdf.
e remaining sections in this chapter are concerned with methods of
drawing conclusions from the sample that can then applied to the larger
phenomenon of interest ( hypothesis testing). e three most important sta-
tistical tests for earth science applications are introduced, these being the
two-sample t-test to compare the means of two data sets, the two-sample
F-test to compare the variances of two data sets, and the χ
2
-test to compare
distributions. e last section introduces methods that can be used to t
distributions to our data sets.
3.6 The t-Test
e Student’s t-test by William Gossett compares the means of two distri-
butions. e one-sample t-test is used to test the hypothesis that the mean
of a Gaussian-distributed population has a value speci ed in the null hy-
pothesis. e two-sample t-test is employed to test the hypothesis that the
means of two Gaussian distributions are identical. In the following text, the
two-sample t-test is introduced to demonstrate hypothesis testing. Let us
assume that two independent sets of n
a
and n
b
measurements have been
carried out on the same object, for instance, measurements on two sets of
rock samples taken from two separate outcrops. e t-test can be used to de-
termine whether both sets of samples come from the same population, e. g.,
the same lithologic unit ( null hypothesis) or from two di erent populations
( alternative hypothesis). Both sample distributions must be Gaussian, and
the variance for the two sets of measurements should be similar. e appro-
priate test statistic for the di erence between the two means is then
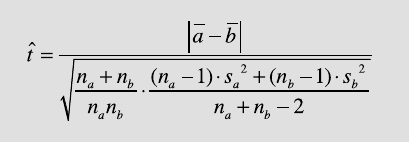
62 3 UNIVARIATE STATISTICS
where n
a
and n
b
are the sample sizes, and s
a
2
and s
b
2
are the variances of
the two samples a and b. e null hypothesis can be rejected if the measured
t-value is higher than the critical t-value, which depends on the number of
degrees of freedom Φ=n
a
+n
b
–2 and the signi cance level α. e signi -
cance level α of a test is the maximum probability of accidentally rejecting
a true null hypothesis. Note that we cannot prove the null hypothesis, in
other words not guilty is not the same as innocent (Fig. 3.12). e hypoth-
esis test can be performed either as a one-tailed (one-sided) or two-tailed
(two-sided) test. e term tail derives from the tailing o of the data to the
far le and far right of a probability density function, as, for example, in
the t distribution. e one-tailed test is used to test against the alternative
hypothesis that the mean of the rst sample is either smaller or larger than
the mean of the second sample at a signi cance level of 5 % or 0.05. e one-
tailed test would require the modi cation of the above equation by replac-
ing the absolute value of the di erence between the means by the di erence
between the means. e two-tailed t-test is used when the means are not
equal at a 5 % signi cance level, i. e., when is makes no di erence which of
the means is larger. In this case, the signi cance level is halved, i. e., 2.5 % is
used to compute the critical t-value.
We can now load an example data set of two independent series of mea-
surements. e rst example shows the performance of the two-sample t-
test on two distributions with means of 25.5 and 25.3, while the standard
deviations are 1.3 and 1.5, respectively.
clear
load('organicmatter_two.mat');
e binary le organicmatter_two.mat contains two data sets corg1 and
corg2. First, we plot both histograms in a single graph
[n1,x1] = hist(corg1);
[n2,x2] = hist(corg2);
h1 = bar(x1,n1);
hold on
h2 = bar(x2,n2);
hold off

3.6 THE T-TEST 63
3 UNIVARIATE STATISTICS
set(h1,'FaceColor','none','EdgeColor','r')
set(h2,'FaceColor','none','EdgeColor','b')
Here we use the command set to change graphic objects of the bar plots h1
and
h2, such as the face and edge colors of the bars. We then compute the
frequency distributions of both samples, together with the sample sizes, the
means and the standard deviations.
[n1,x1] = hist(corg1);
[n2,x2] = hist(corg2);
na = length(corg1);
nb = length(corg2);
ma = mean(corg1);
mb = mean(corg2);
sa = std(corg1);
sb = std(corg2);
Next, we calculate the t-value using the translation of the equation for the
t-test statistic into MATLAB code.
tcalc = abs((ma-mb))/sqrt(((na+nb)/(na*nb)) * ...
(((na-1)*sa^2+(nb-1)*sb^2)/(na+nb-2)))
tcalc =
0.7279
We can now compare the calculated tcalc of 1.7995 with the critical
tcrit. is can be accomplished using the function tinv, which yields
the inverse of the t distribution function with
na-nb-2 degrees of freedom
at the 5 % signi cance level. is is a two-sample t-test, i. e., the means are
not equal. Computing the two-tailed critical
tcrit by entering 1–0.05/2
yields the upper (positive)
tcrit that we compare with the absolute value
of the di erence between the means.
tcrit = tinv(1-0.05/2,na+nb-2)
tcrit =
1.9803
Since the tcalc calculated from the data is smaller than the critical
tcrit, we cannot reject the null hypothesis without another cause. We
conclude therefore that the two means are identical at a 5 % signi cance
level. Alternatively, we can apply the function
ttest2(x,y,alpha) to
the two independent samples
corg1 and corg2 at an alpha=0.05 or a
5 % signi cance level. e command
[h,p,ci,stats] = ttest2(corg1,corg2,0.05)
64 3 UNIVARIATE STATISTICS
yields
h =
0
p =
0.4681
ci =
-0.3028 0.6547
stats =
tstat: 0.7279
df: 118
sd: 1.3241
e result h=0 means that we cannot reject the null hypothesis without an-
other cause at a 5 % signi cance level. e p-value of 0.4681 suggests that the
chances of observing more extreme t values than the values in this example,
from similar experiments, would be 4681 in 10,000. e 95 % con dence in-
terval on the mean is [–0.3028 0.6547], which includes the theoretical (and
hypothesized) di erence between the means of 25.5–25.3=0.2.
e second synthetic example shows the performance of the two-sam-
ple t-test in an example with very di erent means, 24.3 and 25.5, while the
standard deviations are again 1.3 and 1.5, respectively.
clear
load('organicmatter_three.mat');
is le again contains two data sets corg1 and corg2. As before, we rst
compute the frequency distributions of both samples, together with the
sample sizes, the means and the standard deviations.
[n1,x1] = hist(corg1);
[n2,x2] = hist(corg2);
na = length(corg1);
nb = length(corg2);
ma = mean(corg1);
mb = mean(corg2);
sa = std(corg1);
sb = std(corg2);
Next, we calculate the t-value using the translation of the equation for the
t-test statistic into MATLAB code.
tcalc = abs((ma-mb))/sqrt(((na+nb)/(na*nb)) * ...
(((na-1)*sa^2+(nb-1)*sb^2)/(na+nb-2)))

3.6 THE T-TEST 65
3 UNIVARIATE STATISTICS
tcalc =
4.7364
We can now compare the calculated tcalc of 4.7364 with the critical
tcrit. Again, this can be accomplished using the function tinv at a 5 %
signi cance level. e function
tinv yields the inverse of the t distribution
function with
na-nb-2 degrees of freedom at the 5 % signi cance level.
is is again a two-sample t-test, i. e., the means are not equal. Computing
the two-tailed critical
tcrit by entering 1–0.05/2 yields the upper (posi-
tive)
tcrit that we compare with the absolute value of the di erence be-
tween the means.
tcrit = tinv(1-0.05/2,na+nb-2)
tcrit =
1.9803
Since the tcalc calculated from the data is now larger than the critical
tcrit, we can reject the null hypothesis and conclude that the means are
not identical at a 5 % signi cance level. Alternatively, we can apply the func-
tion
ttest2(x,y,alpha) to the two independent samples corg1 and
corg2 at an alpha=0.05 or a 5 % signi cance level. e command
[h,p,ci,stats] = ttest2(corg1,corg2,0.05)
yields
h =
1
p =
6.1183e-06
ci =
0.7011 1.7086
stats =
tstat: 4.7364
df: 118
sd: 1.3933
e result h=1 suggests that we can reject the null hypothesis. e p-value
is extremely low and very close to zero suggesting that the null hypothesis is
very unlikely to be true. e 95 % con dence interval on the mean is [0.7011
1.7086], which again includes the theoretical (and hypothesized) di erence
between the means of 25.5–24.3=1.2.
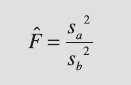
66 3 UNIVARIATE STATISTICS
3.7 The F-Test
e two-sample F-test by Snedecor and Cochran (1989) compares the vari-
ances s
a
2
and s
b
2
of two distributions, where s
a
2
>s
b
2
. An example is the
comparison of the natural heterogeneity of two samples based on replicated
measurements. e sample sizes n
a
and n
b
should be above 30. Both, the
sample and population distributions must be Gaussian. e appropriate test
statistic with which to compare the variances is then
e two variances are signi cantly di erent, i. e., we can reject the null hy-
pothesis without another cause, if the measured F-value is higher than the
critical F-value, which in turn will depend on the number of degrees of free-
dom Φ
a
=n
a
–1 and Φ
b
=n
b
–1, respectively, and the signi cance level α. e
one-sample F-test, in contrast, virtually performs a χ
2
-test of the hypothesis
that the data come from a normal distribution with a speci c variance (see
Section 3.8). We rst apply the two-sample F-test to two distributions with
very similar standard deviations of 1.2550 and 1.2097.
clear
load('organicmatter_four.mat');
e quantity F is the quotient of the larger variance divided by the smaller
variance. We can now compute the standard deviations, where
s1 = std(corg1)
s2 = std(corg2)
which yields
s1 =
1.2550
s2 =
1.2097
e F-distribution has two parameters, df1 and df2, which are the num-
bers of observations of both distributions reduced by one, where
df1 = length(corg1) - 1

3.7 THE F-TEST 67
3 UNIVARIATE STATISTICS
df2 = length(corg2) - 1
which yields
df1 =
59
df2 =
59
Next we sort the standard deviations by their absolute values,
if s1 > s2
slarger = s1
ssmaller = s2
else
slarger = s2
ssmaller = s1
end
and get
slarger =
1.2550
ssmaller =
1.2097
We now compare the calculated F with the critical F. is can be accom-
plished using the function
finv at a signi cance level of 0.05 or 5 %. e
function
finv returns the inverse of the F distribution function with df1
and
df2 degrees of freedom, at the 5 % signi cance level. is is a two-
tailed test and we therefore must divide the p-value of 0.05 by two. Typing
Fcalc = slarger^2 / ssmaller^2
Fcrit = finv(1-0.05/2,df1,df2)
yields
Fcalc =
1.0762
Fcrit =
1.6741
Since the F calculated from the data is smaller than the critical F, we cannot
reject the null hypothesis without another cause. We conclude therefore that
the variances are identical at 5 % signi cance level. Alternatively, we can ap-
ply the function
vartest2(x,y,alpha) to the two independent samples
