Томусяк А.А., Трохименко В.С. Теорія ймовірностей
Подождите немного. Документ загружается.

U
u
1
, u
2
, . . . , u
n
U
X
X x
1
x
2
. . . x
r
P (X = x
k
) p
1
p
2
. . . p
r
n
n
(0; 1) r
p
1
p
1
+ p
2
. . . p
1
+ p
2
+ ··· + p
r−1
p
1
, p
2
, . . . , p
r
I
k
= (p
1
+ p
2
+ ··· + p
k
−
1
; p
1
+ p
2
+ ··· + p
k
).
X

u u ∈
I
k
X x
k
P (X = x
k
) = p
k
P (U ∈ I
k
) = P (p
1
+ p
2
+ ···+ p
k−1
< U < p
1
+ p
2
+ ···+ p
k
) = p
k
,
X = x
k
U ∈ I
k
A p
X
P (X = x
k
) 1 − p p
u (0; p)
A u (p; 1) A
A
1
, A
2
, . . . , A
r
p
1
, p
2
, . . . , p
r
X . . . r
P (X = x
k
) p
1
p
2
. . . p
r
u ∈ (p
1
+p
2
+···+ p
k−1
; p
1
+p
2
+···+ p
k
)
A
k

X
P 0, 5 0, 5
u
u
0, 78; 0, 18; 0, 81, 0, 69; 0, 49; 0, 45; 0, 92; 0, 59; 0, 23; 0, 53.
0, 29; 0, 13; 0, 45; 0, 57; 0, 20; 0, 43; 0, 19; 0, 57; 0, 47; 0, 42.
¤
X
P
1
4
1
2
1
4
u ∈ (0; 0, 25) X
u ∈ (0, 25; 0, 75) X = 1 u ∈
(0, 75; 1) X = 2 γ
¤

n = 5 p =
1
4
X
P (X = k)
n = 6 p =
1
3
X
P (X = k)
X
P (X = k)
p =
1
3
X
P (X = k)
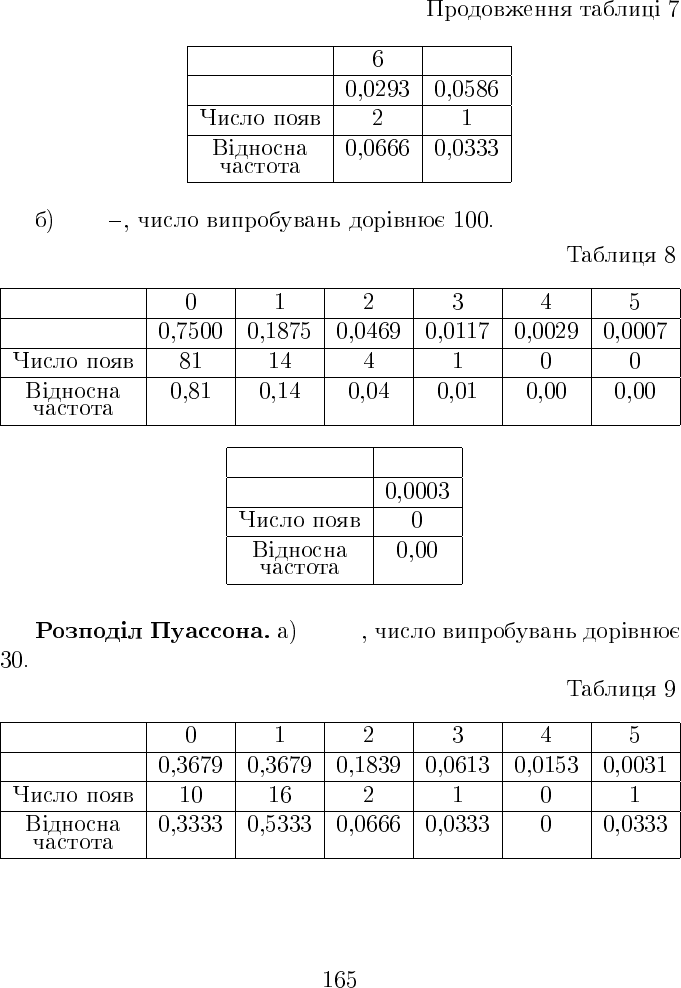
X > 6
P (X = k)
p =
3
4
X
P (X = k)
X > 5
P (X = k)
λ = 1
X
P (X = k)

X > 6
P (X = k)
λ = 2
X
P (X = k)
X > 5
P (X = k)
X
f(x) f(x) > 0
f(x) = 0
F (x)
F
−1
(x) F (x)
f(x) > 0
F (F
−1
(x)) = F
−1
(F (x)) = x.
F (X)
x 0 6 F (x) 6 1

X F (X)
∼
F
(x) = P (F (X) < x) =
=
0, x 6 0,
P (X < F
−1
(x)), 0 < x 6 1,
1, x > 1
=
=
0, x 6 0,
F
(
F
−1
(
x
))
, 0
< x
6
1
,
1, x > 1
=
0, x 6 0,
x, 0
< x
6
1
,
1, x > 1,
F (X)
X
f(x) F (x)
F (X) =
X
Z
−∞
f(t)dt
[0; 1] u
U
F (x) =
x
Z
−∞
f(t)dt = u
X

X
X
F (x) =
0, x 6 1,
x − 1
4
, 1 < x 6 5,
1, x > 5,
x − 1
4
= u,
u
u
1
= 0, 115 u
2
= 0, 662 u
3
= 0, 241 u
4
= 0, 564 u
5
= 0, 355
u
6
= 0, 185 u
7
= 0, 262 u
8
= 0, 038 u
9
= 0, 869 u
10
= 0, 009
X
x
1
= 1, 460, x
2
= 3, 648, x
3
= 1, 964, x
4
= 3, 256, x
5
= 2, 420,
x
6
= 1, 740, x
7
= 2, 048, x
8
= 1, 152, x
9
= 4, 476, x
10
= 1, 036.
X
f(x) =
0, x 6 1,
x −
1
2
, 1 < x 6 2,
1, x > 2.

F (x) =
x
Z
−∞
f(t)dt =
=
0, x 6 1,
x
Z
1
µ
t −
1
2
¶
dt, 1 < x 6 2,
2
Z
1
µ
t −
1
2
¶
dt, x > 2
=
=
0, x 6 1,
x
2
2
−
x
2
, 1 < x 6 2,
1, x > 2.
X
x
2
2
−
x
2
= u x
2
− x − 2u = 0,
x =
1 +
√
1 + 8u
2
2
.
u
1
= 0, 113 u
2
= 0, 845 u
3
= 0, 604 u
4
= 0, 722 u
5
= 0, 294
u
6
= 0, 296 u
7
= 0, 875 u
8
= 0, 270 u
9
= 0, 451 u
10
= 0, 049
X

x
1
= 1, 025, x
2
= 1, 795, x
3
= 1, 490, x
4
= 1, 637, x
5
= 1, 151,
x
6
= 1, 152, x
7
= 1, 835, x
8
= 1, 129, x
9
= 1, 310, x
10
= 1, 005.
X
λ > 0
f(x) =
(
0, x < 0,
λe
−λx
, x > 0.
x
Z
0
λe
−λt
dt = u
1 − e
−λx
= u.
x = −
1
λ
ln(1 − u).
1 − U
U
x = −
1
λ
ln u.
X
a σ
Y =
1
σ
(X − a)
Y
1
√
2π
y
Z
−∞
e
−
t
2
2
dt = u.
