Тиманюк В.А., Животова Е.Н. Биофизика

Подождите немного. Документ загружается.

641

∂

.(90)

Ñóììà ÷àñòíûõ äèôôåðåíöèàëîâ ôóíêöèè íàçûâàåòñÿ ïîëíûì äèôôå-

ðåíöèàëîì:

dddd

uuu

uxyz

xyz

∂∂∂

=++

∂∂∂

.(91)

Åñëè äèôôåðåíöèàëû àðãóìåíòîâ ìàëû, òî ïîëíûé äèôôåðåíöèàë

ôóíêöèè ïðèáëèæåííî ðàâåí ïðèðàùåíèþ ôóíêöèè:

duu≈∆ .(92)

Ïîíÿòèå ïîëíîãî äèôôåðåíöèàëà ìîæåò áûòü ðàñïðîñòðàíåíî íà ôóíê-

öèþ ëþáîãî ÷èñëà íåçàâèñèìûõ ïåðåìåííûõ. Åñëè u ÿâëÿåòñÿ ôóíêöèåé

îäíîãî àðãóìåíòà, òî åäèíñòâåííàÿ ÷àñòíàÿ ïðîèçâîäíàÿ îáðàùàåòñÿ

â îáûêíîâåííóþ, à ïîëíûé äèôôåðåíöèàë — â îáûêíîâåííûé.

8. Ãðàäèåíò ôóíêöèè

Ãðàäèåíòîì ôóíêöèè íàçûâàåòñÿ âåêòîð, ïîêàçûâàþùèé íàïðàâëå-

íèå íàèáîëüøåãî âîçðàñòàíèÿ ñêàëÿðíîé ôóíêöèè ϕ, çíà÷åíèå êîòîðîé

èçìåíÿåòñÿ îò îäíîé òî÷êè ïðîñòðàíñòâà ê äðóãîé. Îáîçíà÷àåòñÿ ñèìâî-

ëîì grad ϕ. Åñëè ϕ = u(x, y, z), òî

grad

uuu

ijk

xyz

∂∂∂

ϕ= + +

∂∂∂





,(93)

ãäå



, j



, k



— åäèíè÷íûå âåêòîðû, íàïðàâëåííûå ñîîòâåòñòâåííî ïî îñÿì

êîîðäèíàò 0x, 0y, 0z.

×àñòî â öåëÿõ óïðîùåíèÿ ãðàäèåíòîì íàçûâàþò ïðîèçâîäíóþ îò ñêà-

ëÿðíîé ôóíêöèè ïî ëþáîìó íàïðàâëåíèþ, íàïðèìåð â íàïðàâëåíèè õ:

Ñòðîãî ãîâîðÿ, ýòà ïðîèçâîäíàÿ ðàâíà ïðîåêöèè ãðàäèåíòà íà íà-

ïðàâëåíèå õ:

(grad)

=ϕ.(94)

9. Íåîïðåäåëåííûé èíòåãðàë

Åñëè ôóíêöèÿ f(x) ÿâëÿåòñÿ ïðîèçâîäíîé ôóíêöèè F(x) èëè f(x) dx

ÿâëÿåòñÿ äèôôåðåíöèàëîì ôóíêöèè F(x):

()d d ()fx x Fx=

òî ôóíêöèÿ F(x) íàçûâàåòñÿ ïåðâîîáðàçíîé ôóíêöèè f(x).

Êðàòêèå ñâåäåíèÿ ïî âûñøåé ìàòåìàòèêå

642

Ëþáàÿ íåïðåðûâíàÿ ôóíêöèÿ f(x) èìååò áåñ÷èñëåííîå ìíîæåñòâî ïåð-

âîîáðàçíûõ, îòëè÷àþùèõñÿ äðóã îò äðóãà ïîñòîÿííûì ñëàãàåìûì Ñ. Ñî-

âîêóïíîñòü âñåõ ïåðâîîáðàçíûõ äàííîé ôóíêöèè f(x) èëè äàííîãî âûðà-

æåíèÿ f(x) dx íàçûâàåòñÿ íåîïðåäåëåííûì èíòåãðàëîì:

()d ()fx x Fx C=+

∫

.(95)

Âûðàæåíèå f(x) dx íàçûâàåòñÿ ïîäûíòåãðàëüíûì âûðàæåíèåì; ôóíê-

öèÿ f(x) — ïîäûíòåãðàëüíîé ôóíêöèåé; ïåðåìåííàÿ õ — ïåðåìåííîé èí-

òåãðèðîâàíèÿ; ïðîèçâîëüíàÿ ïîñòîÿííàÿ Ñ — êîíñòàíòîé èíòåãðèðîâàíèÿ.

Ñâîéñòâà íåîïðåäåëåííîãî èíòåãðàëà

1. Äèôôåðåíöèàë íåîïðåäåëåííîãî èíòåãðàëà ðàâåí ïîäûíòåãðàëüíî-

ìó âûðàæåíèþ:

d()d ()dfx x fx x=

∫

,(96)

èëè ïðîèçâîäíàÿ íåîïðåäåëåííîãî èíòåãðàëà ðàâíà ïîäûíòåãðàëüíîé

ôóíêöèè:

()d ()

fx x fx

∫

.(97)

2. Íåîïðåäåëåííûé èíòåãðàë îò äèôôåðåíöèàëà ôóíêöèè ðàâåí ñóì-

ìå ýòîé ôóíêöèè è êîíñòàíòû èíòåãðèðîâàíèÿ:

d() ()fx fx C=+

∫

.(98)

3. Ïîñòîÿííûé ìíîæèòåëü à ìîæíî âûíîñèòü çà çíàê èíòåãðàëà:

()d ()dafxxafxx=

∫∫

.(99)

4. Èíòåãðàë àëãåáðàè÷åñêîé ñóììû ðàâåí àëãåáðàè÷åñêîé ñóììå èí-

òåãðàëîâ:

123

[ ( ) ( ) ( )]d ( )d ( )d ( )dfx fx fx x fx x fx x fx x+− = + −

∫∫∫∫

. (100)

Îñíîâíûå íåîïðåäåëåííûå èíòåãðàëû (a, n, c = const)

dax axC=+

∫

;(101)

xx C

∫

()

1n ≠−

;(102)

∫

;(103)

ed e

xC=+

∫

;(104)

Ïðèëîæåíèå 1

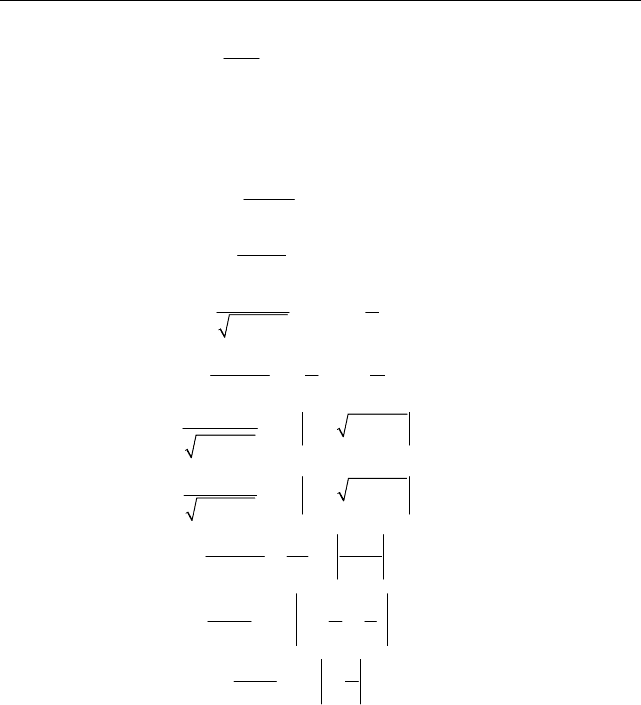
643

ax C

∫

()

0; 1aa>≠;(105)

sin d cosxx x C=− +

∫

;(106)

cos d sinxx x C=+

∫

;(107)

cos

∫

;(108)

ctg

sin

=− +

∫

;(109)

arcsin

−

∫

; (110)

arctg

∫

; (111)

xxaC

=+++

∫

; (112)

xxaC

=+−+

−

∫

; (113)

xxa

axa

−

∫

; (114)

ln tg

cos



=++





∫

; (115)

ln tg

sin 2

∫

. (116)

Îñíîâíûå ìåòîäû èíòåãðèðîâàíèÿ

1. Ìåòîä ïîäñòàíîâêè:

()d [ ( )] ( )dft t f x x x

′

=ϕϕ

∫∫

, ãäå ( )tx=ϕ . (117)

2. Èíòåãðèðîâàíèå ïî ÷àñòÿì:

udv uv vdu=−

∫∫

. (118)

10. Îïðåäåëåííûé èíòåãðàë

Ïóñòü äàíà ôóíêöèÿ y = f(x). Âûáåðåì íà îñè õ òî÷êè a è b è âîññòàíî-

âèì èç íèõ ïåðïåíäèêóëÿðû äî ïåðåñå÷åíèÿ ñ ôóíêöèåé (ðèñ. 6). Äëÿ

âû÷èñëåíèÿ ïëîùàäè ïîëó÷åííîé êðèâîëèíåéíîé òðàïåöèè ðàçîáüåì îò-

Êðàòêèå ñâåäåíèÿ ïî âûñøåé ìàòåìàòèêå

644

ðåçîê [a, b] íà ìàëûå ïðîìåæóòêè

è âûäåëèì âíóòðè êàæäîãî i-ãî îòðåç-

êà ïðîìåæóòî÷íóþ òî÷êó k

. Òîãäà

ïëîùàäü i-ãî ïðÿìîóãîëüíèêà áóäåò

ðàâíà ( )

fk x∆ , à ñóììà ïëîùàäåé —

ïëîùàäè êðèâîëèíåéíîé òðàïåöèè.

Ïðåäåë, ê êîòîðîìó ñòðåìèòñÿ ñóììà

()

fk x

∆

∑

, êîãäà íàèáîëüøàÿ èç

äëèí âñåõ ÷àñòè÷íûõ ïðîìåæóòêîâ

ñòðåìèòñÿ ê íóëþ, íàçûâàåòñÿ îïðå-

äåëåííûì èíòåãðàëîì è îáîçíà÷àåòñÿ:

()d

fx x

∫

(119)

(÷èòàåòñÿ «èíòåãðàë îò a äî áý ýô îò èêñ äý èêñ»). Êîíöû a è b äàííîãî

ïðîìåæóòêà (ïðîìåæóòêà èíòåãðèðîâàíèÿ) íàçûâàþòñÿ ïðåäåëàìè èíòåã-

ðàëà — íèæíèì (a) è âåðõíèì (b).

Äëÿ íàõîæäåíèÿ îïðåäåëåííîãî èíòåãðàëà ïîëüçóþòñÿ ôîðìóëîé Íüþ-

òîíà—Ëåéáíèöà:

()d () ()

fx x Fb Fa=−

∫

, (120)

ãäå F(x) — ïåðâîîáðàçíàÿ ôóíêöèè f(x), òî åñòü F'(x) = f(x).

Ñâîéñòâà îïðåäåëåííîãî èíòåãðàëà

1. Ïðè îäèíàêîâûõ ïðåäåëàõ èíòåãðèðîâàíèÿ îïðåäåëåííûé èíòåãðàë

ðàâåí íóëþ:

()d 0

fx x

∫

. (121)

2. Ïðè ïåðåñòàíîâêå ïðåäåëîâ èíòåãðèðîâàíèÿ îïðåäåëåííûé èíòåã-

ðàë ñîõðàíÿåò àáñîëþòíîå çíà÷åíèå, íî ìåíÿåò çíàê íà ïðîòèâîïîëîæ-

íûé:

()d ()d

fx x fx x=−

∫∫

. (122)

3. Åñëè äàí ðÿä ÷èñåë a, b, c, … , k, l, ðàñïîëîæåííûõ â êàêîì óãîäíî

ïîðÿäêå, òî

()d ()d ()d ... ()d

lbc l

aab k

fx x fx x fx x fx x=+++

∫∫∫ ∫

. (123)

Ðèñ. 6. Ê âû÷èñëåíèþ îïðåäåëåííîãî

èíòåãðàëà

Ïðèëîæåíèå 1

645

Ïðàêòè÷åñêè âàæåí ñëó÷àé, êîãäà ÷èñëà a, b, c, … , k, l âçÿòû â ïîðÿäêå

âîçðàñòàíèÿ èëè óáûâàíèÿ.

4. Èíòåãðàë àëãåáðàè÷åñêîé ñóììû íåèçìåííîãî ÷èñëà ñëàãàåìûõ ðà-

âåí àëãåáðàè÷åñêîé ñóììå èíòåãðàëîâ îòäåëüíûõ ñëàãàåìûõ:

1123

[ ( )d ( )d ( )]d ( )d ( )d ( )d

bbbb

aaaa

fxx fxx fx x fxx fxx fxx+− = + −

∫∫∫∫

.(124)

5. Ïîñòîÿííûé ìíîæèòåëü ìîæíî âûíîñèòü çà çíàê èíòåãðàëà:

()d ()d

Afxx Afxx=

∫∫

, ãäå constA = . (125)

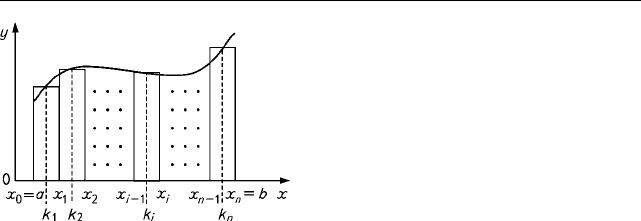
11. Êðèâîëèíåéíûé èíòåãðàë

Ïóñòü â ïîëå íåêîòîðîãî âåê-

òîðà a



(íàïðèìåð, ñèëû



, íà-

ïðÿæåííîñòè ýëåêòðè÷åñêîãî



èëè ìàãíèòíîãî H



ïîëåé)

çàäàíà êðèâàÿ L (ðèñ. 7). Ðàçî-

áüåì åå íà ìàëûå äóãè

∆

, êàæ-

äîé èç êîòîðûõ ñîîòâåòñòâóåò

îïðåäåëåííîå çíà÷åíèå âåêòîðà



. Ñîñòàâèì ïðîèçâåäåíèå äóãè

∆

è ïðîåêöèè âåêòîðà



íà

äóãó ∆l:

cos

iii

alα⋅∆ ,

ãäå

α — óãîë ìåæäó âåêòîðîì



è êàñàòåëüíîé ê äóãå â òî÷êå ïðèëîæå-

íèÿ âåêòîðà



Ñóììà ýòèõ ïðîèçâåäåíèé ïðè íåîãðàíè÷åííîì âîçðàñòàíèè è ñòðåì-

ëåíèè äëèí âñåõ äóã ê íóëþ íàçûâàåòñÿ êðèâîëèíåéíûì èíòåãðàëîì:

cos cos d

lim

iii

alal

∆→

α∆ = α

∑

∫

. (126)

Ýëåìåíòàðíûé ó÷àñòîê dl êðèâîé L ìîæíî ðàññìàòðèâàòü êàê âåêòîð.

Òîãäà êðèâîëèíåéíûé èíòåãðàë çàïèøåòñÿ ÷åðåç ñêàëÿðíîå ïðîèçâåäå-

íèå:

cos d d

alalα=

∫∫



. (127)

Èíîãäà ïðîèçâåäåíèå cosa α, òî åñòü ïðîåêöèþ âåêòîðà à íà íàïðàâ-

ëåíèå dl îáîçíà÷àþò à

, òîãäà âûðàæåíèå äëÿ êðèâîëèíåéíîãî èíòåãðàëà

ïðèíèìàåò âèä:

Ðèñ. 7. Ê îïðåäåëåíèþ êðèâîëèíåéíîãî

èíòåãðàëà

Êðàòêèå ñâåäåíèÿ ïî âûñøåé ìàòåìàòèêå

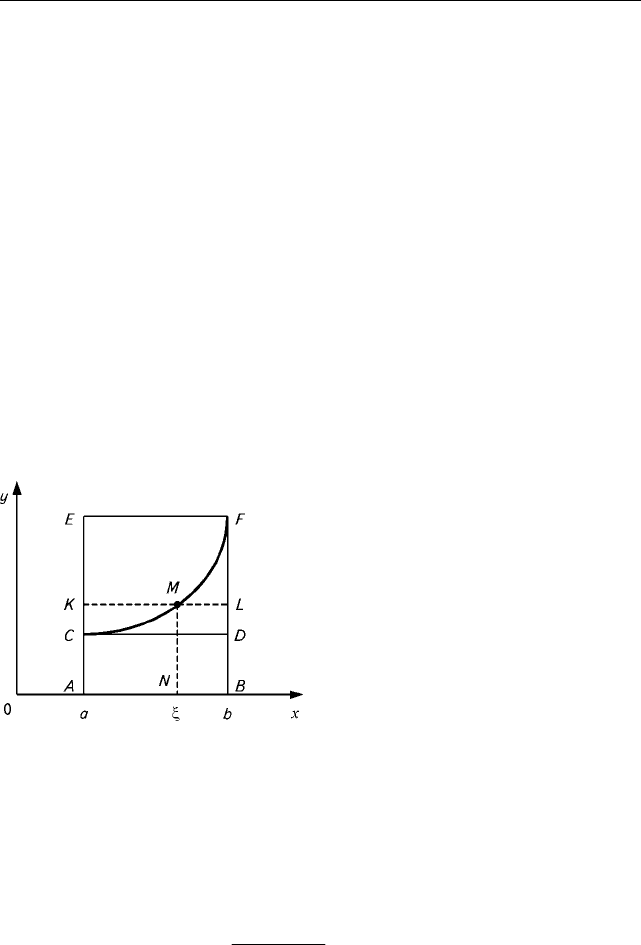
646

∫

. (128)

Êðèâîëèíåéíûé èíòåãðàë ïî çàìêíóòîé êðèâîé (ïî çàìêíóòîìó êîí-

òóðó) íàçûâàåòñÿ öèðêóëÿöèåé è îáîçíà÷àåòñÿ:

∫



. (129)

12. Òåîðåìà î ñðåäíåì

Òåîðåìà î ñðåäíåì èíòåãðàëüíîãî èñ÷èñëåíèÿ: ïóñòü äàíà ôóíêöèÿ f(x),

íåïðåðûâíàÿ íà ïðîìåæóòêå [a, b]. Òîãäà îïðåäåëåííûé èíòåãðàë ôóíê-

öèè f(x) íà ïðîìåæóòêå [a, b] ðàâåí ïðîèçâåäåíèþ äëèíû ýòîãî ïðîìåæóò-

êà íà ñðåäíåå çíà÷åíèå ôóíêöèè íà äàííîì ïðîìåæóòêå:

()d ( ) ()

fx x ba f=− ξ

∫

, (130)

ãäå ab≤ξ≤ .

Ïîÿñíèì ýòî íà ñëåäóþùåì ïðèìåðå. Êðèâàÿ FC (ðèñ. 8) ÿâëÿåòñÿ

ãðàôèêîì ôóíêöèè f(x) íà ïðîìåæóòêå [a, b]. Áóäåì ñìåùàòü îòðåçîê KL

èç íà÷àëüíîãî ïîëîæåíèÿ CD ê êî-

íå÷íîìó ïîëîæåíèþ EF. Â íà÷àëå

äâèæåíèÿ ïëîùàäü ïðÿìîóãîëüíè-

êà AKLB ìåíüøå, ÷åì çíà÷åíèå

()d

fx x

∫

, à â êîíöå — áîëüøå (íà-

ïîìíèì, ÷òî ( ) d

fx x

∫

÷èñëåííî

ðàâåí ïëîùàäè êðèâîëèíåéíîé òðà-

ïåöèè, îãðàíè÷åííîé ôóíêöèåé f(x),

îñüþ õ è ïðÿìûìè x = a è x = b).

Òîãäà äîëæíî íàéòèñü êàêîå-òî ïðî-

ìåæóòî÷íîå ïîëîæåíèå, ãäå èìååò

ìåñòî ðàâåíñòâî

()d

AKLB

Sfxx=

∫

Îñíîâàíèåì ïðÿìîóãîëüíèêà AKLB ñëóæèò AB = b – a, à âûñîòîé —

îòðåçîê NM, äëèíà êîòîðîãî ðàâíà çíà÷åíèþ ôóíêöèè f(x) â òî÷êå ξ.

Äàííàÿ òåîðåìà ìîæåò áûòü ñâåäåíà ê âèäó:

() ()

()

fb fa

−

′

=ξ

−

, (131)

òî åñòü ê òåîðåìå î ñðåäíåì äèôôåðåíöèàëüíîãî èñ÷èñëåíèÿ (ô î ð ì ó ë å

Ëàãðàíæà).

Ðèñ. 8. Ê òåîðåìå î ñðåäíåì

Ïðèëîæåíèå 1

647

13. Äèôôåðåíöèàëüíûå óðàâíåíèÿ

Äèôôåðåíöèàëüíûì óðàâíåíèåì íàçûâàåòñÿ óðàâíåíèå, ñîäåðæàùåå

ïðîèçâîäíûå íåèçâåñòíîé ôóíêöèè (èëè íåñêîëüêèõ íåèçâåñòíûõ ôóíê-

öèé). Âìåñòî ïðîèçâîäíûõ â óðàâíåíèå ìîãóò âõîäèòü äèôôåðåíöèàëû.

Îáùèé âèä äèôôåðåíöèàëüíîãî óðàâíåíèÿ ñ îäíîé íåèçâåñòíîé ôóíê-

öèåé:

()

( , , , , ..., ) 0

Fxyy y y

′′′

= . (132)

Ïîðÿäêîì äèôôåðåíöèàëüíîãî óðàâíåíèÿ íàçûâàåòñÿ ïîðÿäîê íàèâûñ-

øåé èç ïðîèçâîäíûõ, âõîäÿùèõ â ýòî óðàâíåíèå. Åñëè íåèçâåñòíûå ôóíê-

öèè çàâèñÿò îò îäíîãî àðãóìåíòà, òî äèôôåðåíöèàëüíîå óðàâíåíèå íàçû-

âàåòñÿ î á û ê í î â å í í û ì; åñëè îò íåñêîëüêèõ, òî — äèôôåðåíöèàëüíûì

óðàâíåíèåì ñ ÷àñòíûìè ïðîèçâîäíûìè. Ïðèìåðîì ïîñëåäíåãî òèïà óðàâíå-

íèé ÿâëÿåòñÿ âîëíîâîå óðàâíåíèå:

222 2

22222

1SSS S

xyzvt

∂∂∂ ∂

++=⋅

∂∂∂ ∂

. (133)

Ôóíêöèÿ y = f(x) íàçûâàåòñÿ ðåøåíèåì äèôôåðåíöèàëüíîãî óðàâíåíèÿ

n-ãî ïîðÿäêà, åñëè ïîñëåäíåå îáðàùàåòñÿ â òîæäåñòâî äëÿ âñåõ x ∈ (a, b)

ïîñëå ïîäñòàíîâêè ýòîé ôóíêöèè è åå ïðîèçâîäíûõ â óðàâíåíèå. Ïîäðà-

çóìåâàåòñÿ, ÷òî ôóíêöèÿ y = f(x) n ðàç íåïðåðûâíî äèôôåðåíöèðóåìà íà

ïðîìåæóòêå (a, b).

Ëþáîå äèôôåðåíöèàëüíîå óðàâíåíèå âèäà (132) èìååò áåñêîíå÷íîå

ìíîæåñòâî ðåøåíèé, êîòîðûå ìîãóò áûòü çàïèñàíû â âèäå:

(, , , , )

yyxCC C= … , (134)

ãäå

, , ...,

CC C — ïðîèçâîëüíûå ïîñòîÿííûå; n — ïîðÿäîê äèôôåðåí-

öèàëüíîãî óðàâíåíèÿ.

Âûðàæåíèå (134) íàçûâàåòñÿ îáùèì ðåøåíèåì äèôôåðåíöèàëüíîãî óðàâ-

íåíèÿ. Îòìåòèì, ÷òî ïðè ðåøåíèè ïðàêòè÷åñêèõ çàäà÷ íàèáîëüøèé èí-

òåðåñ ïðåäñòàâëÿåò ðåøåíèå, óäîâëåòâîðÿþùåå íà÷àëüíûì óñëîâèÿì:

()

yx y= ,

()

00,1

yx y

′

= ,

()

00,2

yx y

′′

= , …,

()

00,1

yxy

−

= . Ïîèñê òàêîãî

ðåøåíèÿ íàçûâàåòñÿ ç à ä à ÷ å é Ê î ø è. Ðåøåíèå çàäà÷è Êîøè íàçû-

âàåòñÿ ÷ à ñ ò í û ì ð å ø å í è å ì. Ñîâîêóïíîñòü âñåõ ÷àñòíûõ ðåøåíèé

îáðàçóåò îáùåå ðåøåíèå.

Ñïðàâåäëèâà ñëåäóþùàÿ òåîðåìà ñóùåñòâîâàíèÿ è åäèíñòâåííîñòè ðåøå-

íèÿ çàäà÷è Êîøè. Åñëè ïðàâàÿ ÷àñòü óðàâíåíèÿ

() ( )

()

, , , , ...,

yfxyyyy

−

′′′

è åå ÷àñòíûå ïðîèçâîäíûå ïî ïåðåìåííûì y ,

′

, y

′′

, …,

()

−

íåïðå-

ðûâíû â ðàññìàòðèâàåìîé îáëàñòè G, òî äëÿ ëþáîé òî÷êè

(

000,1

,, ,xyy

)

0,2 0, 1

,...,

−

èç G íà íåêîòîðîì èíòåðâàëå

()

,xhxh−+ ñóùåñòâóåò

åäèíñòâåííîå ðåøåíèå ó(x) óðàâíåíèÿ, óäîâëåòâîðÿþùåå íà÷àëüíûì óñ-

ëîâèÿì

()

yx y= ,

()

00,1

yx y

′

= ,

()

00,2

yx y

′′

= , …,

()

00,1

yxy

−

= .

Ãðàôèê ðåøåíèÿ äèôôåðåíöèàëüíîãî óðàâíåíèÿ íàçûâàåòñÿ èíòåã-

ðàëüíîé êðèâîé äèôôåðåíöèàëüíîãî óðàâíåíèÿ.

Êðàòêèå ñâåäåíèÿ ïî âûñøåé ìàòåìàòèêå

648

Äèôôåðåíöèàëüíûå óðàâíåíèÿ øèðîêî èñïîëüçóþòñÿ äëÿ îïèñàíèÿ,

ìîäåëèðîâàíèÿ è èññëåäîâàíèÿ ôèçè÷åñêèõ, õèìè÷åñêèõ, áèîëîãè÷åñêèõ,

ýêîíîìè÷åñêèõ ïðîöåññîâ. Äàëüøå áóäóò ðàññìîòðåíû äèôôåðåíöèàëü-

íûå óðàâíåíèÿ, íàèáîëåå ÷àñòî âñòðå÷àþùèåñÿ â ôèçèêå è áèîôèçèêå.

Óðàâíåíèåì ñ ðàçäåëÿþùèìèñÿ ïåðåìåííûìè íàçûâàåòñÿ óðàâíåíèå ïåð-

âîãî ïîðÿäêà âèäà:

11 2 2

dd0XY x XY y+=, (135)

ãäå ôóíêöèè X

, X

, Y

è Y

íåïðåðûâíû, ïðè÷åì ôóíêöèè X

è X

çàâèñÿò

òîëüêî

îò õ, à ôóíêöèè Y

è Y

— òîëüêî îò y. Äåëåíèåì íà Y

òàêîå

óðàâíåíèå ìîæåò áûòü ïðèâåäåíî ê âèäó:

XxYy

+=. (136)

Ïîëó÷åííîå óðàâíåíèå íàçûâàåòñÿ óðàâíåíèåì ñ ðàçäåëåííûìè ïåðåìåí-

íûìè. Ïðîöåññ ïðèâåäåíèÿ íàçûâàåòñÿ ð à ç ä å ë å í è å ì ï å ð å ì å í-

í û õ. Îáùåå ðåøåíèå óðàâíåíèÿ (135) èìååò âèä:

xyC

∫∫

, ãäå constC = . (137)

Â òåõ ñëó÷àÿõ, êîãäà îáùåå ðåøåíèå íå ñóùåñòâåííî, ÷àñòíîå ðåøå-

íèå óäîáíî îïðåäåëÿòü ïî ôîðìóëå:

dd0

∫∫

, (138)

ãäå x

è y

— íà÷àëüíûå çíà÷åíèÿ.

Ëèíåéíûì äèôôåðåíöèàëüíûì óðàâíåíèåì n-ãî ïîðÿäêà íàçûâàåòñÿ óðàâ-

íåíèå âèäà

()

() () ()

...

yaxy axyaxyfx

−

′

++++=, (139)

ãäå y = y(x) — íåèçâåñòíàÿ ôóíêöèÿ; a

(x), a

(x), …, a

n–1

(x), a

(x), f(x) —

èçâåñòíûå ôóíêöèè, êîòîðûå áóäåì ïîëàãàòü íåïðåðûâíûìè íà ïðîìå-

æóòêå (a, b).

Óðàâíåíèÿ

()

() ()

... 0

yaxy axyaxy

−

′

++++= (140)

()

() () () ()

... , 0

y axy a xy a xy fx fx

−

′

++++= ≠. (141)

íàçûâàþòñÿ ñîîòâåòñòâåííî ëèíåéíûìè äèôôåðåíöèàëüíûìè óðàâíåíèÿìè n-ãî

ïîðÿäêà áåç ïðàâîé ÷àñòè (îäíîðîäíûìè) è ñ ïðàâîé ÷àñòüþ (íåîäíîðîäíûìè).

Îäíà èç íèõ èëè îáå ìîãóò áûòü ïîñòîÿííûìè, òî æå ñïðàâåäëèâî äëÿ ôóíê-

öèé Y

è Y

Ïðèëîæåíèå 1

649

Åñëè ìíîæèòåëè a

, a

, …, a

íå çàâèñÿò îò x, òî åñòü ÿâëÿþòñÿ ïîñòî-

ÿííûìè, òî òàêîå äèôôåðåíöèàëüíîå óðàâíåíèå íàçûâàåòñÿ ëèíåéíûì äèô-

ôåðåíöèàëüíûì óðàâíåíèåì ñ ïîñòîÿííûìè êîýôôèöèåíòàìè. Åãî ðåøåíèå

ðàçûñêèâàåòñÿ â âèäå e

= .

Äàëåå áóäåò ðàññìîòðåí àëãîðèòì îòûñêàíèÿ ðåøåíèé ëèíåéíûõ óðàâ-

íåíèé âòîðîãî ïîðÿäêà, êîòîðûé ìîæåò áûòü îáîáùåí äëÿ ëèíåéíûõ óðàâ-

íåíèé ïðîèçâîëüíîãî ïîðÿäêà.

Äëÿ îòûñêàíèÿ ðåøåíèÿ îäíîðîäíîãî ëèíåéíîãî äèôôåðåíöèàëüíîãî

óðàâíåíèÿ

ñ ïîñòîÿííûìè êîýôôèöèåíòàìè

0yayay

′′ ′

++= (142)

ñëåäóåò:

1) çàïèñàòü õ à ð à ê ò å ð è ñ ò è ÷ å ñ ê î å ó ð à â í å í è å:

0aaλ+ λ+ = ; (143)

2) íàéòè êîðíè ýòîãî óðàâíåíèÿ:

λ è

λ ;

3) çàïèñàòü âûðàæåíèå äëÿ îáùåãî ðåøåíèÿ:

() () ()

11 22

yx Cy x C y x=+, (144)

ãäå

()

= ;

()

= — ëèíåéíî íåçàâèñèìûå ðåøåíèÿ óðàâíå-

íèÿ (141).

Âîçìîæíû ñëåäóþùèå òðè ñëó÷àÿ:

à) äèñêðèìèíàíò óðàâíåíèÿ (142) ïîëîæèòåëåí:

40aa−>. Òîãäà

óðàâíåíèå èìååò äâà íåðàâíûõ äåéñòâèòåëüíûõ êîðíÿ:

1,2 2

λ=− ± − .

Îáùåå ðåøåíèå óðàâíåíèÿ (141):

()

yx C C

λλ

=+; (145)

á) äèñêðèìèíàíò óðàâíåíèÿ (142) ðàâåí 0:

40aa−=. Òîãäà óðàâíå-

íèå èìååò äâà îäèíàêîâûõ êîðíÿ:

λ=λ=− .

Îäíîðîäíîå ëèíåéíîå óðàâíåíèå ïåðâîãî ïîðÿäêà

() 0yPxy

′

ÿâëÿåòñÿ óðàâ-

íåíèåì ñ ðàçäåëÿþùèìèñÿ ïåðåìåííûìè, è åãî îáùåå ðåøåíèå âû÷èñëÿåòñÿ ïî

ôîðìóëå

() exp ()d

yx C Px x



=−





∫

, ãäå C — ïðîèçâîëüíàÿ ïîñòîÿííàÿ.

Êðàòêèå ñâåäåíèÿ ïî âûñøåé ìàòåìàòèêå

650

Â ýòîì ñëó÷àå â âûðàæåíèè äëÿ îáùåãî ðåøåíèÿ óðàâíåíèÿ (141) ïî-

ìèìî ðåøåíèÿ

x−

ïðèñóòñòâóåò ëèíåéíî íåçàâèñèìîå ðåøåíèå

−

òî åñòü îáùåå ðåøåíèå èìååò âèä:

()

yCCx

−

=+ (146)

3) äèñêðèìèíàíò óðàâíåíèÿ (143) îòðèöàòåëåí:

40aa−<. Òîãäà

õàðàêòåðèñòè÷åñêîå óðàâíåíèå èìååò êîìïëåêñíûå êîðíè:

1,2

iλ=−±γ,

ãäå

γ= − . Ïðèìåíèâ ôîðìóëó Ýéëåðà (17), ïîëó÷àåì ëèíåéíî íå-

çàâèñèìûå ðåøåíèÿ óðàâíåíèÿ (142):

ecos; esin

yxyx

−−

=γ=γ, (147)

ïðè ýòîì îáùåå ðåøåíèå èìååò âèä:

()

ecos sin

yCxCx

−

=γ+γ. (148)

Ïîñëå òðèãîíîìåòðè÷åñêèõ ïðåîáðàçîâàíèé óðàâíåíèå (148) ìîæåò

áûòü ñâåäåíî ê âèäó:

()

esin

yC C x

−

=+γ, (149)

ãäå

341

sinCCC= ;

342

cosCCC= , èëè

()

ecos

yC C x

−

=+γ, (150)

ãäå

561

cosCCC= ;

562

sinCCC−=.

Äëÿ ðåøåíèÿ çàäà÷è Êîøè íóæíî ïîäñòàâèòü âûðàæåíèå äëÿ îáùåãî

ðåøåíèÿ â íà÷àëüíûå óñëîâèÿ è îïðåäåëèòü çíà÷åíèÿ ïîñòîÿííûõ

C ,

êîòîðûå ÿâëÿþòñÿ ðåøåíèÿìè ñèñòåìû ëèíåéíûõ àëãåáðàè÷åñêèõ óðàâ-

íåíèé:

() ()

11 0 22 0 0

11 0 22 0 0,1

;

Cy x Cy x y







′′





(151)

Îáùåå ðåøåíèå ëèíåéíîãî íåîäíîðîäíîãî óðàâíåíèÿ

()

yayayfx

′′ ′

++= (152)

Ïðèëîæåíèå 1