Тихоненков В.А. Конструирование и надежность измерительно-вычислительных комплексов летательных аппаратов
Подождите немного. Документ загружается.

121
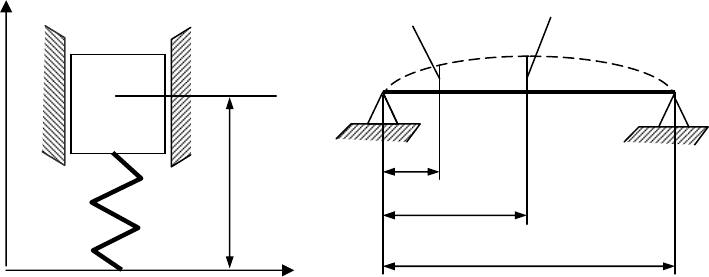
3) Снижение амплитуды резонансных колебаний за счет применения
специальных амортизирующих устройств, которые проектируются как систе-
ма упругодемпфирующих опор (амортизаторов) на которые устанавливается
РЭА с целью защиты от механических воздействий. Блок РЭА на амортиза-
торах образует колебательную систему, параметры которой выбирают так,
чтобы вибрация в месте установки блока на носителе передавалась на блок
ослабленной до допустимого уровня. Недостатки данного способа аналогич-
ны первому способу.
8.1. Анализ колебаний плат при вибрации.
С точки зрения теории механических колебаний плата может рассматри-
ваться как механическая система, анализ колебаний которой начинается с оп-
ределения числа степеней свободы, действующих сил и составления уравне-
ния движения [16, 22].
Степени свободы.
Числом степеней свободы называется минимальное число независимых
координат, однозначно определяющих положение всех материальных точек
системы в любой момент времени.
Любая механическая система имеет бесконечное число материальных
точек и поэтому имеет бесконечное число степеней свободы. Однако для ре-
шения практических задач реальные конструкции представляют упрощенны-
ми схемами, имеющими одну или несколько степеней свободы. В таких схе-
мах:
– некоторые части считают лишенными массы и представляют в виде
деформируемых без инерционных связей;
– другие, имеющие значительные массы, считают или материальны-
ми точками или абсолютно твердыми телами.
a) Z б) V
o
⋅
⋅⋅
⋅sin π
ππ
π⋅
⋅⋅
⋅x ⁄
⁄⁄
⁄l V
o
m
•
••
•
•
••
• •
••
•
x
Z
i
К l
/2
l
Рис. 8.1

122
На рисунке 8.1а. представлена схема системы с одной степенью свободы,
состоящая из абсолютно твердого тела массой m, установленной на упругом
элементе жесткостью к. Так как тело имеет перемещение только вдоль оси
Z, то координата z
i
полностью определяет положение системы.
Иногда в расчетной схеме как бы признается, что инерцией, упругостью
и другими свойствами обладают все элементы системы, но ограничение чис-
ла степеней достигается априорным заданием конфигурации системы при ко-
лебаниях. Например для балки рисунок 8.1б. ось прогиба может быть пред-
ставлена выражением
l
x
tVtxV
o
⋅
⋅=
π
sin)(),(
.
То есть, данная система так же обладает одной степенью свободы и про-
гиб в любой точке может быть определен по одной известной величине V
o
(t).
Силы.
Силы, действующие на колебательную систему можно разделить на
внутренние и внешние. Внутренние определяются свойствами самой системы
и делятся на восстанавливающие, силы трения и инерционные силы.
Восстанавливающими силами являются силы упругости. Если между си-
лой и вызванной ею деформацией линейная зависимость, то упругие системы
с одной степенью свободы характеризуются коэффициентом жесткости к.
к = F/z .
Силы трения (диссипативные силы) приводят к рассеянию (диссипации)
энергии механических колебаний. К ним относятся силы трения в опорах и
сочленениях между элементами конструкции, внутренние силы трения в ма-
териалах элементов конструкции, силы сопротивления среды. Эти силы зави-
сят от скорости и амплитуды деформации и имеют направление противопо-
ложное скорости.
Силы инерции системы, определяются ее массой и ускорением. Их на-
правление совпадает с направлением перемещения.
К внешним силам относятся силы, действующие от внешних источников,
от корпуса самолета или ракеты, от вращения неуравновешенного ротора
электродвигателя и т.д.
Уравнения движения.
При составлении уравнения движения используют три способа – основ-
ной, прямой и обратный. Так как прямой способ описания уравнения движе-
ния наиболее простой и часто применяется описания систем с конечным чис-
лом свободы, то рассмотрим именно его.

123
В этом случае массы мысленно отделяются от упругого скелета системы
и для каждой из них записывают дифференциальное уравнение движения.
Например для система показанной на рис. 1.а. уравнение имеет вид:
0
=
⋅
+
⋅
z
k
z
m
&
&
, (8.1)
где
z
m
&
&
⋅
− сила инерции системы;
k
⋅
z – сила упругости системы.
Так как силы трения и возмущающие силы отсутствуют, то это уравне-
ние описывает свободные колебания системы без затухания. Допустим, что
состояние равновесия этой системы нарушено, тогда уравнение движения
(6.1) можно представить:
0
2
=⋅+ zz
o
ω
&&
,
где
m
к
o
=
ω
− постоянная, определяемая свойствами системы.
Очевидно, что частными решениями данного дифференциального урав-
нения являются:
z = C
1
⋅ sin
ω
o
⋅
t + C
2
⋅cos
ω
o
⋅
t ,
где С
1
и С
2
– постоянные, определяемые из начальных условий.
Последнее выражение можно так же представить в виде:
z = A⋅ sin (
ω
o
⋅
t +
α
) ,
где
2
2
2
1
ССА +=
− амплитуда колебаний;
1
2
C
C
arctg=
α
− начальная фаза.
Из уравнения видно, что движение повторяется через период времени
2
⋅π
. Тогда период колебаний можно обозначить Т = 2
⋅π⁄ω
о
, а
ω
о
имеет смысл
круговой частоты.
При воздействии вибраций на основание (корпус изделия), на котором
закреплен объект (плата), считая что колебание основания описываются гар-
моническим законом и, представляя колебательную систему в виде, пред-
ставленном на рис. 8.2, можно записать:
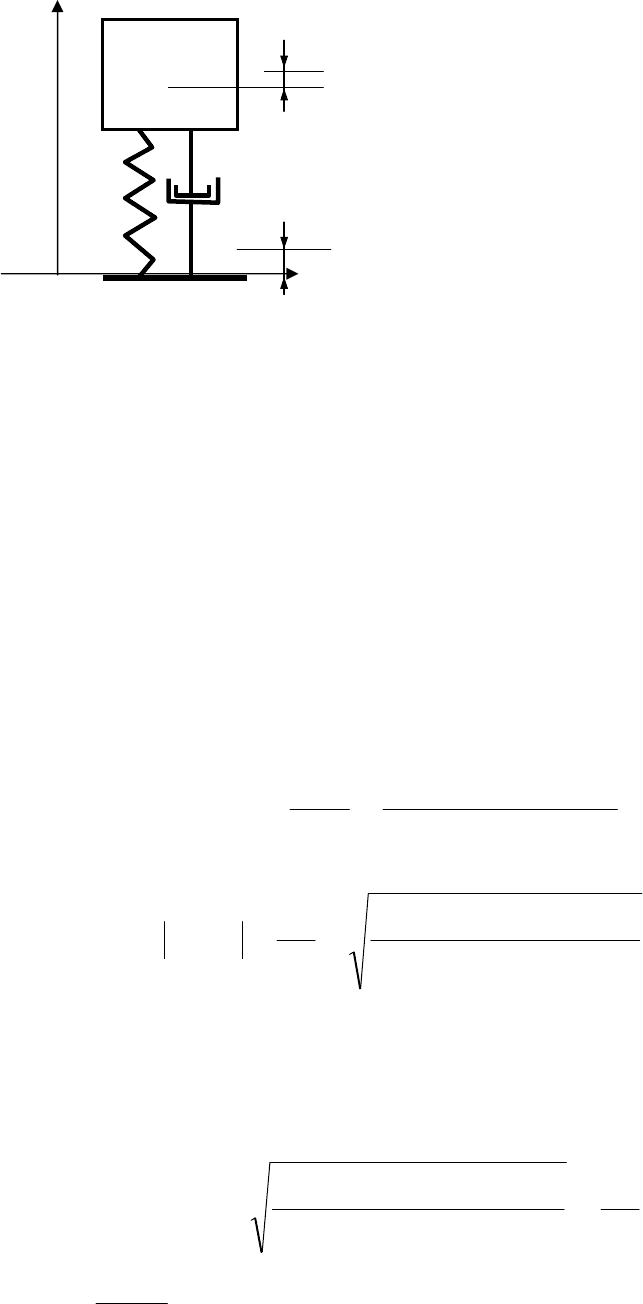
124
Z z
1
(t)
= z
01
⋅
e
i
⋅ω⋅
t
m z
Уравнение движения имеет вид:
•
0)()(
1
1
=
−
⋅
+
−
⋅
+
⋅
zzкzzbzm &&&&
.
к b
Преобразуем уравнение к виду.
z
1
1
1
zкzbzкzbzm
⋅
+
⋅
=
⋅
+
⋅
+
⋅
&&&&
.
Рис. 8.2 И будем искать колебание системы
в форме:
z(t) = z
o
⋅
e
i
⋅ω⋅
t
Подставляя z(t) и z
1
(t) в уравнение движения и учитывая, что
)()()()(
22
tztzitz ⋅−=⋅⋅=
ωω
&& и
)
(
)
(
t
z
i
t
z
⋅
⋅
=
ω
&
,
получим:
(
)
(
)
ωωω
⋅⋅+⋅=⋅⋅+⋅−⋅ biкtzbimкtz )()(
1
2
Тогда передаточная функция будет равна:
ωω
ω
ω
⋅⋅+⋅−
⋅
⋅
+
==
bimк
biк
tz
tz
к
в
2
1
)(
)(
)(
,
а ее модуль:
( )
22
2
2
222
1
)(
ωω
ω
ω
⋅+⋅−
⋅+
==
bmк
bк
z
z
к
o
o
в
.
Поделив числитель и знаменатель подкоренного выражения на к, и вво-
дя понятие
λ
, получим выражение для коэффициента динамичности при
вибрациях:
1
22222
224
4)(
4
o
o
o
o
с
z
z
=
⋅⋅+−
⋅⋅+
=
ωλωω
ωλω
µ
, (8.2)
где
к
b
o
2
2
ω
λ
⋅
=⋅
− относительный коэффициент демпфирования платы;
125
Из выражения (8.2), умножая обе части на
ω
2
и решая относительно
z
o
⋅ω
2
= W
oнес
, получим:
W
oнес
=
µ
с
⋅
W
01
, (8.3)
где W
01
– амплитуда первой формы колебаний.
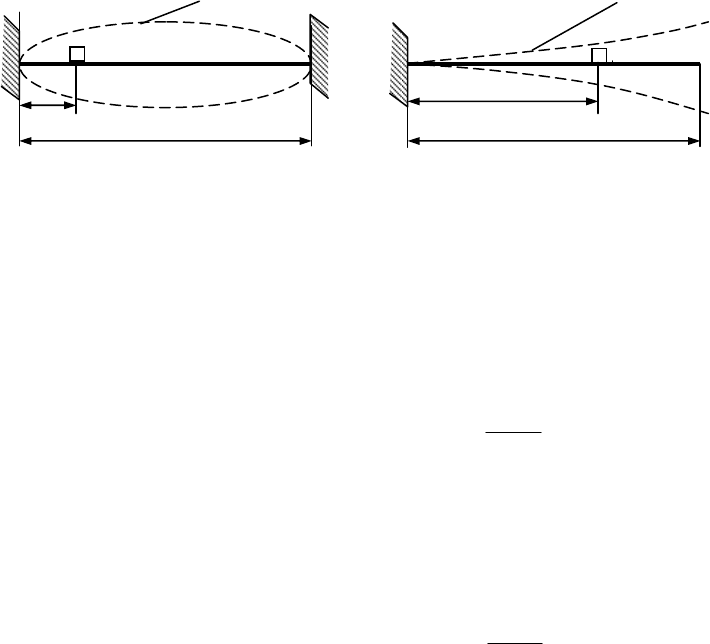
Если плата закреплена с двух сторон (см. рис. 8.3а.), то можно считать,
что амплитуды первой формы колебаний распределены по свободной стороне
длиной l по полуволне синуса.
a) б)
форма колебаний форма колебаний
ЭРЭ ЭРЭ
х х
l l
Рис. 8.3
Поэтому для ЭРЭ, расположенного на плате на расстоянии х от одной
из заделок, уровень ускорений вибраций будет равен:
l
x
WW
oннеiнне
⋅
⋅=
π
sin
. (8.4)
Для платы закрепленной с одной стороны, аналогично рассуждая, полу-
чим (см. рис. 8.3б.):
⋅
−⋅=
l
x
WW
oннеiнне
π
sin1
. (8.5)
Типичный вид зависимости амплитуды W
oнес
ускорения от частоты
ω
внешних вибраций при собственной частоте платы
ω
о
, имеет место резо-
нанс, заключающийся в существенном превышении амплитуды виброускоре-
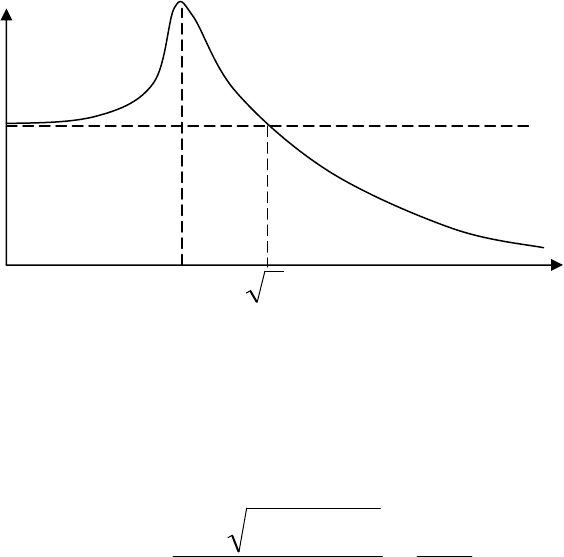
126
ний платы W
oнес
, над амплитудой ускорений внешних вибраций W
01
(см. рис.
8.4).
W
oнес
W
01
ω
ω
о
2
Рис. 8.4
Для реальных конструкций 2
⋅λ
<<
ω
о
, тогда для резонанса коэффициент
динамичности будет равен:
λ
ω
ωλ
λωω
µ
ωω
⋅
=
⋅⋅
⋅+⋅
=
=
22
4
|
22
o
o
oo
с
o
.
Экспериментально установлено, что при вибрации на резонансе печат-
ные платы усиливают виброускорение в десятки раз (
µ
с
= 10…200), причем
это усиление тем больше, чем выше собственная частота платы
ω
о
.
Оценив значение виброускорений, воздействующих на ЭРЭ в соответст-
вии с (8.2) – (8.5), можно определить условие при котором используемая ЭРЭ
будет выдерживать заданные нагрузки:
W
iдоп
>
W
iнес
, (8.6)
где W
iдоп
– допустимый уровень виброускорений для данного ЭРЭ.
Откуда видно, что для оценки работоспособности ЭРЭ, конструктор
должен определить собственные частоты и коэффициент демпфирования
проектируемых плат, а также управлять их значениями. С другой стороны
конструктор может обеспечить выполнение условия (8.6) путем подбора эле-
ментной базы с соответствующими W
iдоп
, которые приводятся в литературе и
ТУ на ЭРЭ. В таблице 8.1 приведены данные по допустимым уровням меха-
нических воздействий для некоторых типов ЭРЭ [21, 24].

127
Таблица 8.1
Тип ЭРЭ Вибрации Многократные удары Линейное уско-
рение
W
доп
[g]
f
н
– f
в
[Гц]
W
доп
[g]
W
доп
[g]
τ
ττ
τ
[мс]
Микросхемы
К140,К118
К155
КР565
К580,КР589
КМ155
К500
5 – 600
5 – 600
1 – 2000
1 – 600
1 – 2000
1 – 600
5
5
10
10
10
10
15
15
75
75
75
75
2 – 15
2 – 15
2 – 6
2 – 6
2 – 6
2 – 6
25
25
50
25
50
25
Резисторы
МЛТ
С2-22
С1-8,С2-8
СП5-2В
5 – 5000
5 – 80
5 – 5000
1 – 2500
20
7.5
40
15
40
15
150
75
2 – 10
2 – 15
1 – 3
2 – 6
100
50
100
50
Конденсато-
ры
К73-22,
К73-П-2
К50-6
К50-24
К52-1
1 – 3000
1 – 3000
1 – 600
1 – 1000
1 – 5000
20
20
10
10
20
40
40
15
15
75
2 – 10
2 – 10
2 – 15
2 – 15
2 – 6
200
200
100
50
200
Разъемы
СНП-34
ГРПМ-2
ГРПМ-1
2РМ
1 –2000
5 – 2500
5 – 4000
1 – 5000
10
15
30
50
40
35
35
100
2 – 10
2 – 80
2 – 80
2 – 80
25
50
50
200
8.2. Расчет собственных частот плат.
Для расчета собственных частот колебаний упругих систем применяют
точный и приближенный методы расчета.
Точный расчет основан на составлении уравнений свободных колебаний,
которые для систем с распределенными параметрами представляют уравне-
ния в частных производных четвертой степени, и последующим их интегри-
ровании. Применяется для конструкций простой формы с простейшими спо-
собами крепления.
Приближенные методы, из которых наибольшее применение нашли
энергетические методы Релея и Ритца, не требуют составления и интегриро-
вания дифференциальных уравнений движения и используются для конст-
рукций более сложной конфигурации, неоднородных по толщине, имеющие
точечные нагрузки и более сложные способы крепления. Поэтому будем рас-
сматривать приближенный метод расчета собственных частот реальных плат
[21, 23, 25].

128
Для прямоугольной платы, выполненной из однородного изотропного
упругого материала для всех случаев закрепления краев пластины собствен-
ную частоту можно определить по формуле:
h
qD
a
f
o
⋅
⋅
⋅⋅
⋅
=
ρ
α
π
2
2
1
,
где
( )
2
3
112
µ
−⋅
⋅
=
hE
D
− цилиндрическая жесткость пластины;
а − длина пластины;
µ − коэффициент Пуассона;
ρ − плотность материала пластины;
α − коэффициент, зависящий от способа закрепления
сторон пластины;
q − ускорение свободного падения;
h – толщина пластины.
Значение
α
определяется из решения дифференциального уравнения
колебаний прямоугольной пластины для заданных краевых условий. При-
ближенные решения таких уравнений можно найти по методу Релея – Ритца.
При этом вычисления весьма трудоемки. Поэтому конструкторы используют
другую формулу, выведенную Карпушиным В.Б., в которой формула Релея –
Ритца приводится в виду:
5
2
10
a
hc
f
o
⋅
=
Гц. , (8.7)
где
( )
ρµ
π
α
⋅⋅
⋅
⋅=
2
-112
2
qE
c
− частотная постоянная.
Частотная постоянная зависит от способа крепления и отношения длин
большей стороны к меньшей (a/b) через коэффициент
α
.
Различают сплошное и точечное закрепление. Формула дана для различ-
ных видов сплошного закрепления. При сплошном закреплении крепится од-
на или несколько сторон целиком. Различают следующие случаи сплошного
закрепления сторон платы:
- зажатый край (жесткое защемление);
- опертый край (шарнирное опирание);
- свободный край.
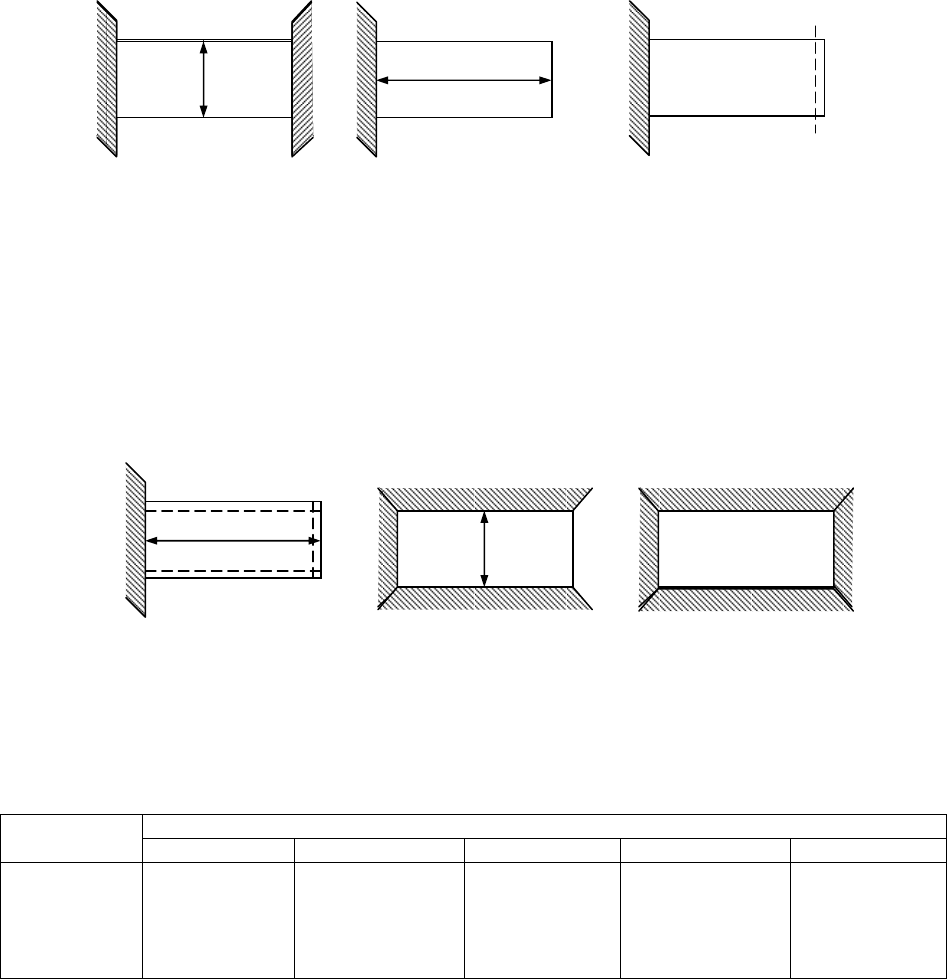
129
Эти три случая являются идеализацией реальных способов закрепления.
Закрепление сторон платы в направляющих блока принимают за шарнирное
опирание. Зажатым краем считается край платы с много контактным разъе-
мом с жесткими выводами (например типа ГРПМ, СНП-34).
В литературе приводятся значения частотной постоянной для различных
способов сплошного крепления сторон и соотношения сторон платы [21].
Для способов крепления, показанных на рис. 8.5. Частотная постоянная
не зависит от соотношения сторон.
b a
a) б) в)
Рис. 8.5
Для плат с креплением в соответствии с рис. 8.5а. – с = 52; для рис. 8.5б.
– с =8,2; для плат с одной защемленной, а другой опертой стороной (рис.
8.5в.) – с = 35,8. Частотные постоянные для других распространенных видов
сплошного закрепления, показанных на рис. 8.6, приведены в таблице 8.2.
a
b
a б в
Рис. 8.6
Таблица 8.2
Схема
Закрепления
Соотношение сторон а/b
1 1,5 2 2,5 3
Рис. 5.6а.
Рис. 5.6b.
Рис. 5.6с.
55
56,2
83,8
81,8
120,9
141,4
120,7
211,7
228,7
171,5
328,6
343,7
234,1
471,4
485,4
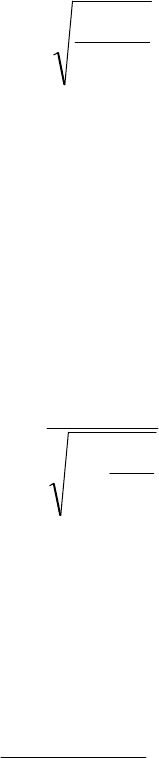
130
При расчете собственной частоты платы с соотношением сторон не сов-
падающим со значениями, приведенными в таблице, значение частотной по-
стоянной можно найти интерполяцией соответствующих табличных данных
или по графику, построенному по ним в соответствующем масштабе. Если
плата изготавливается не из стали, то в формулу собственной частоты вво-
дится поправочный коэффициент на материал в виде:
ρ
ρ
⋅
⋅
=
с
с
м
Е
Е
к
,
где Е и
ρ
− модуль упругости и плотность применяемого материала;
Е=(2 – 2)⋅10
11
Н/м
2
− модуль упругости стали;
ρ
с
=7,8⋅10
3
кг/м
3
− плотность стали.
Расчет (см. формулу 8.7) дан для ненагруженной ЭРЭ платы. Если же
плата равномерно нагружена, то в формулу вводят поправочный коэффици-
ент на вес ЭРЭ, закрепленной на плате:
пл
э
в
Р
Р
к
+
=
1
1
,
где Р
э
и Р
пл
– вес ЭРЭ, размещенной на плате и вес платы соответственно.
Следовательно формулу для приближенного определения собственной
частоты основного тона нагруженной печатной платы можно записать в виде:
[
]
Гц
а
hскк
f
вм
o
5
2
10⋅
⋅
⋅
⋅
=
, (8.8)
где h и а следует брать в [мм.].
Для вычисления собственных частот по приведенным формулам необхо-
димо знать Е,
ρ
и
µ
материала платы. Однако печатные платы представляют
собой неоднородную пластину, состоящую из нескольких слоев различных
материалов. Например плата на основе стеклотекстолита состоит обычно из
4-х слоев: медного слоя, слоя из стеклоткани, слоя фольгированного диэлек-
трика и слоя стеклотекстолита. В литературе приводятся данные по этим по-
казателям для наиболее широко используемых для изготовления плат мате-
риалов [21, 40]. В таблице 8.3 приведены некоторые из этих данных.
