Тевяшев А.Д., Литвин О.Г. Вища математика. Загальний курс: Збірник задач та вправ
Подождите немного. Документ загружается.

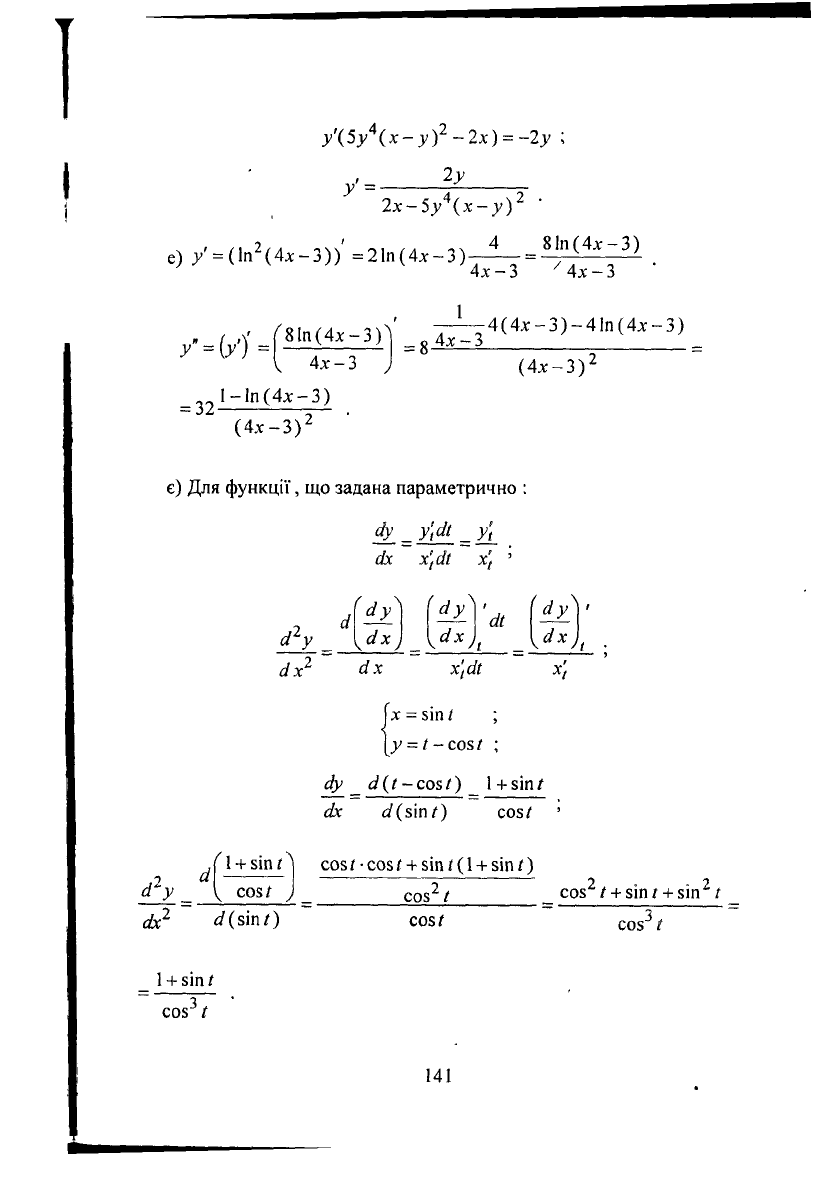
у'(5у\х-у)
2
-2х)
=
-2у ;
2у
У
=
2х-5у\х-у)
2
е)
/ =
(1п
2
(4х-3))'=21п(4х-3)
І
^-
= ^^
4х-3
4х-3
У
=
=
32
{у1
=
Г8Ш(4х-3)У
=
^4(4х-3)-4.п(4х-3)
V
4х-3
1-1п(4х-3)
(4х-3)
2
(4х-3)'
є)
Для
функції,
що
задана параметрично
Ф_
=
УІ^І_
=
УІ_
_
сбс
Х^ЙЇ х^ '
^у_
сіх
2
сі X
сії
х^йї
СІХ
її
ах
2
,(1 +
5ІПҐ
Л
СОВІ
а"
(зіп/)
х
=
зіп<
;
[_у
=
/-со5/
;
ау
_
а"(і-сові)
_
1
+
зіп/
ах
сІ($ті)
сові
С05Ґ-С08/
+
8ІПГ(1
+
5ІПҐ)
соз
і
соз і'
2
• -2
соз
і
+ зіп
і
+ зіп
І
соз
л
І
1
+
зіп/
СОЗ
3
/
141

Задача 3. Знайти границі, використовуючи правило Лопиталя :
е
&тх
-е
х
—
а) Ііт— ; б) Ііт (е
х
+ 2х)
3
* .
Х->0
51ПХ-Х
х->+°о
Розв'язання.
а) Маємо невизначеність типу |^-|. Застосовуючи тричі правило Ло-
питаля , одержуємо
е
шх_
е
х
е
шх
со
5х
~е
х
е
тх
соз
2
х-е*
тх
&тх-е
х
Ііт —: = Ііт : = Ііт
<_>()
5ІП
X
—
X
х
-»0
СОЗХ-1
х
_>0
—
ЗІП
X
.
е
ітх
соз
3
х +
е
5Ш
х
2 соз х (- зіп х) -
е
5
"
1
х
соз хзіп х - е"
тх
СОЗX
- е
х
Ііт
х->0
-СОЗХ
1+0-0-1-1
-1
•
=
1
.
б) Маємо невизначеність типу {со°} . Перетворимо вираз, що стоїть
під знаком границі, для чого скористаємось основною логарифмічною то-
тожністю
а
І0§
"
Ь
= Ь :
\_
і і
(е
х
+2х)
3
х
=е
1піе +2х)
"
=
е
3х
Отже,
_!_
, 1п(е*+2х)
Ііт (е
х
+2х) ' =е
Зх
Х->+оо
л,
• ,.
1п(е
х
+2х)
. [оо]
У виразі Ііт —- маємо невизначеність типу і — к Застосо-
Х->+оо Зх [оо]
вуємо правило Лопиталя :
1
'„X
(е
х
+ 2)
Х-»+оо
1 ..
е
х
+2
1 .. е
х
1
=
—
Ііт = - Ііт =
—
Зх-*+»
е
х
+2х 3 е
х
+ 2 3''
142

Остаточно одержуємо :
Ііт (е
х
+2х)
3х
= е
3
= Уе .
Задача 4. Дослідити задану функцію методами диференціального чис-
лення і побудувати її графік :
„2
а) у = х(х
+
\)
б) У-
Іпх
Розв'язання, а) Область визначення функції у = х(х + \) -вся чис-
лова пряма Ох , тобто х є К..
Функція не є ані парною , ані непарною , тобто
у(-х)
=
-х(-х
+
\)'
і
Ф{ '
* [-У(х).
Для знаходження точок перетину графіка функції з осями координат
покладемо х = 0 =>у = 0; у = 0 =>х = 0 і
дг
= -1.
Функція неперіодична.
Знаходимо інтервали монотонності функції та екстремуми :
/ = 0 + 1)
3
+Зд-(л- + 1)
2
=(х + 1)
2
(х + 1+3х) = (д- + 1)
2
(4л-+1) , •
у'
= 0 при х = -1 і х = -— . Подальше розв'язання можна оформити у виг-
ляді таблиці:
X
(-*;-і)
-1
Н)
1
4
(-Н
У'
0
-
0
-1-
У
0
екстремуму
немає
\
27
256
тіп
Знаходимо інтервали вгнутості і опуклості та точки перегину графіка
функції:
143
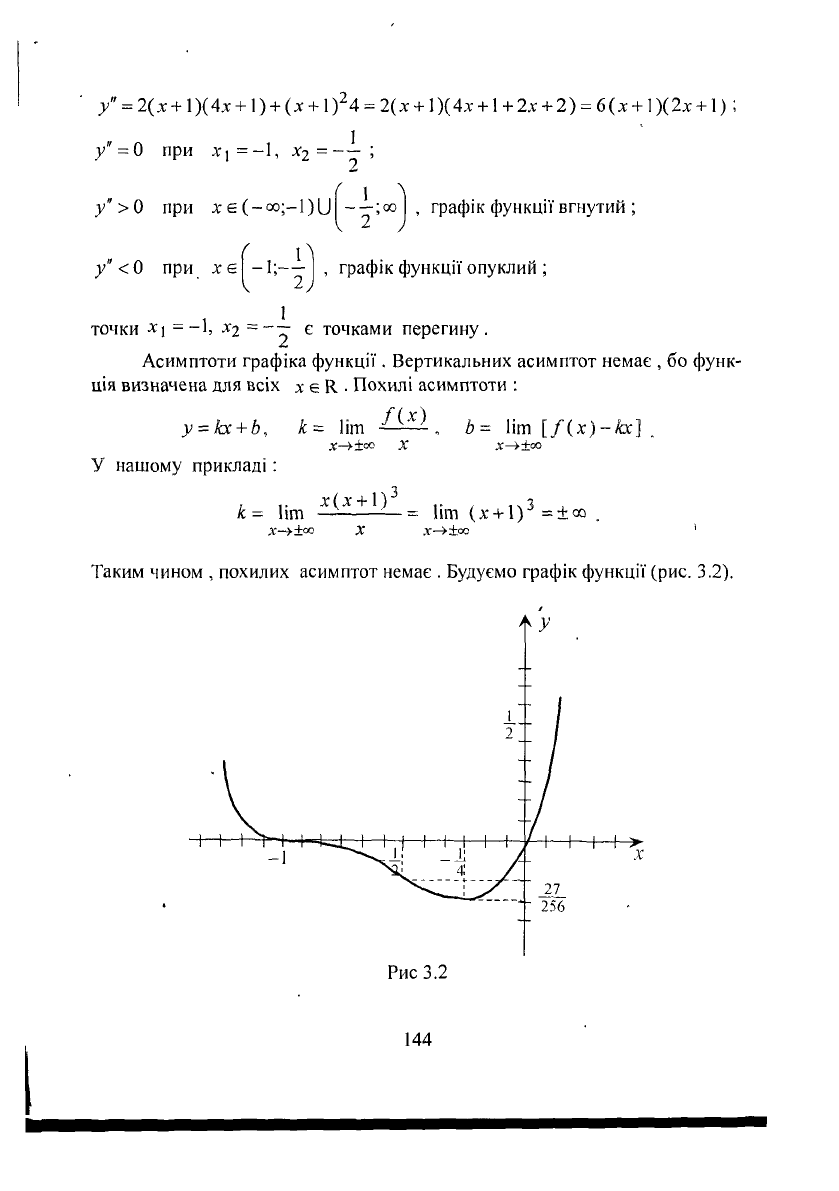
у"
=
2(х
+
1)(4х
+
\)
+
(х
+
\)
2
4
=
2(х
+
ї)(4х
+
\
+
2х
+
2)
=
6(х
+
])(2х
+
\) ;
у"
= 0 при
лг)=-1,
х
2
=-—;
у">0
при
хє(-оо;-1)И
—;оо
| , графік функції вгнутий ;
V 2
У<0 при
хе\-1;~—
], графік функції опуклий ;
,
1
точки *і —і, *2
=_
2"
Є точками
перегину.
Асимптоти графіка функції. Вертикальних асимптот немає , бо функ-
ція визначена для всіх х є Я
•
Похилі асимптоти :
у
=
кх
+
Ь, к= Ііт
х->±°°
х
У нашому прикладі:
Ь= Ііт [/(х)-кх]
к = Ііт — — = Ііт (х + 1) =±°° .
X—>±°°
X X—»±°с '
Таким чином , похилих асимптот немає . Будуємо графік функції (рис. 3.2).
Рис 3.2
144

б) Область визначення функції у = -— : х є (0 ; 1)
СІ
(1 ; аз) .
Іпх
Функція не є ані парною , ані непарною .
Знаходимо точки перетину графіка функції з осями координат . З віссю
Оу графік не перетинається , бо х
Ф
0 ; з віссю Ох він також не перети-
нається .
Функція неперіодична.
Знаходимо інтервали монотонності функції і екстремуми :
2х1пх-х
і
х
_2х1пх-х_х(21пх-1)
(Іпх)
2
(ІпхГ
(ІпхГ
у'
= 0 при
X
= е
2
= Ге , враховуючи область визначення функції. Подаль-
ше розв'язання можна оформити у вигляді таблиці:
X
(0;1)
1
(1;^)
Ге
1
У
-
не існує
-
0
+
|
У
X
не існує
екстремуму
немає
2е
тіп
Знаходимо інтервали вгнутості і опуклості та точки перегину графіка
функції:
2П-ІПХ + Х- 1-І
і 1
(ІпхГ
-(2х1пх-х) 21пх--
(Іпх)
2х(Іпх + 1)(1пх)
2
-2(2х1пх-х)Іпх _ 21пх[х(1пх + 1)1пх-(2х1пх-х)]
х(1пх)
4
х
(1пх)
4
2 х(1пх)
2
+х1пх-2х!пх + х 2х (Іпх)
2
-Іпх + іК 2(1п
2
х- 1пх + 1)
х(1пх)
х(1пх)
Іп
3
х
145
точок перегину немає , бо у" не обертається в нуль ні за якого значення х;
у"
> 0
прихє(1;оо),
графік функції вгнутий ; у" < 0 при х є (0; 1), графік
функції опуклий.
Знаходимо асимптоти графіка функції. Оскільки Ііт у =
+<х>
,
х->1+0
Ііт у = -со,то х =
1
- вертикальна асимптота. Знаходимо похилі асимп-
х-И-0
/їх)
тоти: у = кх +
Ь
, де к = Ііт , Ь= Ііт [/(х)-кх].
Х->±<»
X
Х->±со
Маємо
х 1
к = Ііт = Ііт — = Ііт х = +оо .
х->+оо
ІП
X х—•+<» 1
х—>+оо
X
Таким чином, похилих асимптот немає .
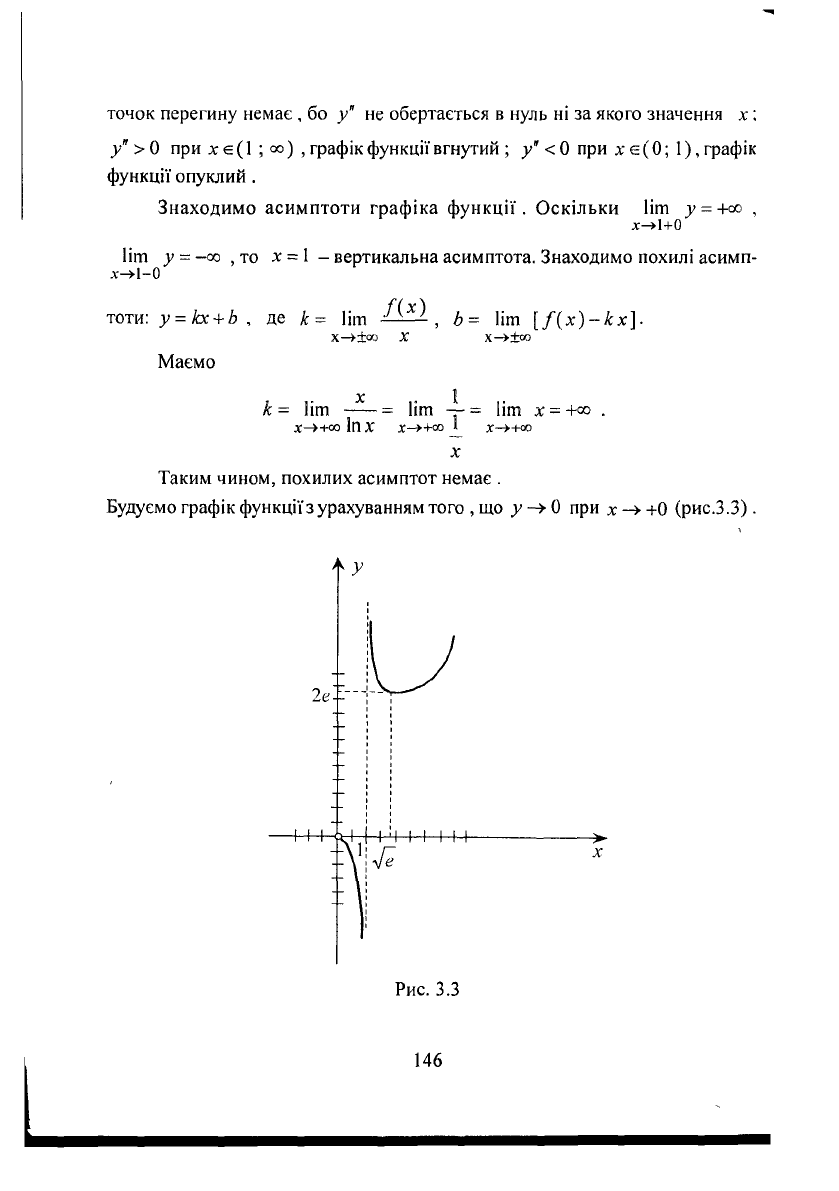
Будуємо графік функції з урахуванням того , що у
~>
0 при х -» +0 (рис.3.3).
Лу
Рис.
3.3
146

Задача 5. Задано функцію ? = $т
2
(х-а у). Показати , що вона задо-
2 д
2
і д
2
і ...
вольняє рівнянню а
т-
=
т-
; перевірити справедливість рівності
дх
2
ду
2
д
2
2 д
2
2
дхду дудх
Розв'язання.
Знаходимо частинні похідні функції г = зіп
2
(я
-
-аг у)
ді
— = 2зіп (х-ау)со$(х-а у) = зіп (2х- 2 а у) ;
дх
д
2
г
—"-г-
= соз
(2.1'
- 2<ту)• 2 = 2соз(2х-2ау) ;
дх
1
дг
= 2 зіп (х-а у) соз
(А-
-а у)(-а) = -а зіп (2х-2ау) ;
д у
д
2
2
ду
1
д
2
2
дхд у
д
2
г
д удх
2
-асо&(2х-2а у)(-2а) = 2а соз(2д:-2ау) ;
= соз (2х- 2 а у) (-2а) = -2а сов (2х-2а у) ;
•
-а соз (2л--2огу)-2 = -2а соз (2х - 2 а у) .
д
2
г д
2
г 2 д г д •?
Звідси видно , що = , а також , що а г- = —у
,
тобто фун-
дхду дудх дх
1
ду
2
кція г(х,у) дійсно задовольняє даному рівнянню .
147

ГЛАВА
4. ІНТЕГРАЛИ, ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ І РЯДИ
4.1.
Невизначений інтеграл
[2,
гл. 5, §5.1-5.17]
Функція Г(х) називається первісною функції /(х) на інтервалі
(а, Ь) , якшо Р'(х) = /(х), хє(а,6).
Якщо /(х) має дві первісні, вони відрізняються на сталу . Іншими
словами, якщо /
г
'(х) = /(х) і Ф'(х) = /(х), то Р(х) = Ф(х) + С .
С = сопзі. Звідси випливає , що існування однієї первісної Г(х) для /(х)
тягне за собою існування безлічі первісних для /(х) вигляду Р(х) + С .
Сукупність усіх первісних для функції / (х) на інтервалі (а, Ь) нази-
вається невнзначеним інтегралом від функції / (х) на цьому інтервалі і
позначається |/(х)(іх .
Такимчином, \/(х) а
,
х = Г(х)
+
С , Г(х) = /(х).
Таблиця основних невизначених інтегралів
2.
5.
6
СОЗХ ЙХ = 5ІП Х + С .
СОЗ
X
148
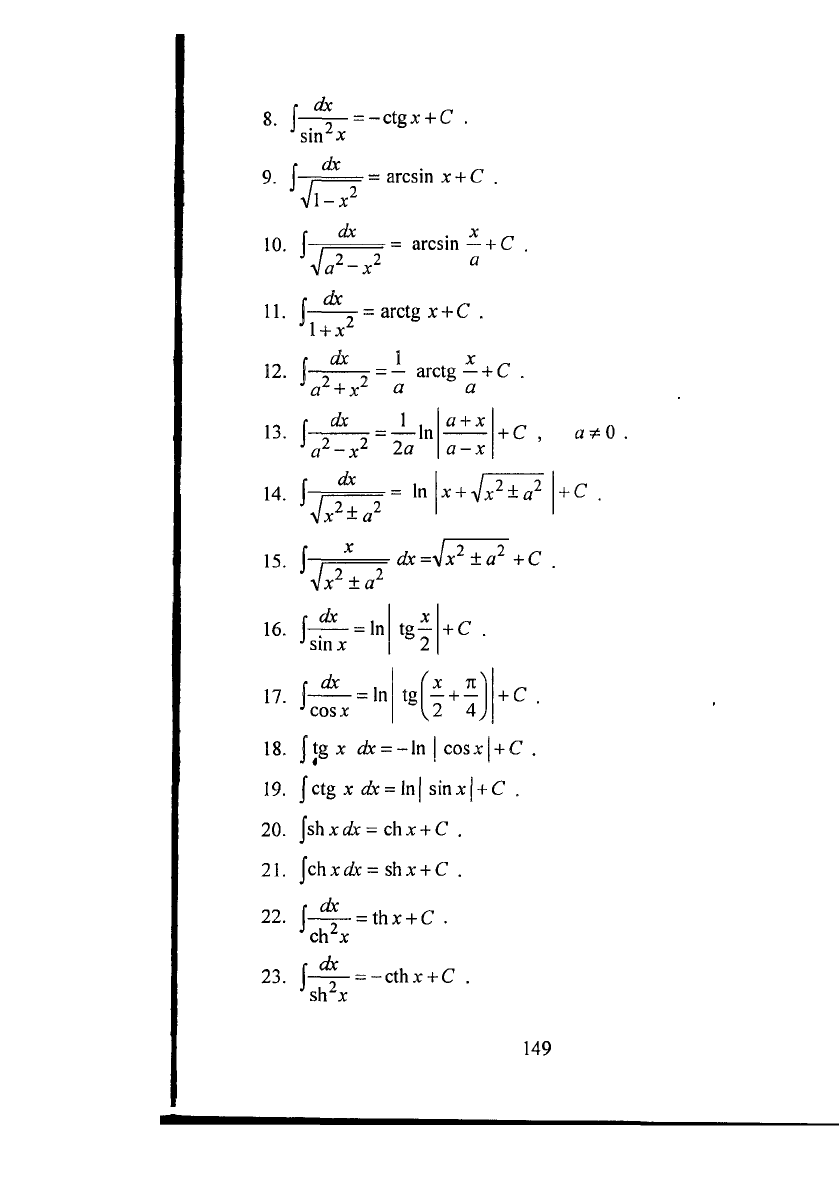
8[
9-і'
сіх
зіп
2
*
сіх
7
ю.
г.
•-СІ&Х
+ С .
= агсзіп
х
+
С .
1-х'
сіх
^х
2
= агсзіп
—
+ С .
12.
|
,3.
[
14./-
15-
X-
!«.
І
17.
/•
А:
1+х
2
ах
=
агсІ§
х + С .
1
х _
агсі§
— + С
а
2
+ х
2
о а
сіх
а
2
-X
і
2а
1п
а
+ х
+
С ,
сіх
УІх
2
±а
:
х
ЦТ7
2
сіх
•=
1п
х
+ 4х
2
±а
2
а*0
+ С
ах=4х
2
±а
2
+С
51ПХ
ах
созх
1п
1п
2
(
+
С .
X
ТІ
1
2
4
+
С
18.
||§х
<&
= -1п |
созх|
+ С
19.
|СІ§
х ах =
1п| зіпх|
+ С .
20.
|зЬхах
= сЬх + С .
21.
|сК
х
ох
=
зЬ
х
+
С .
22.
Г.
Л
23.
[
сЬ
2
х
ох
зЬ
2
х
шх
+
С
.
=
-стх
+ С
.
149

Властивості невизначеного інтеграла
:
1°.
(\/(Х)СІХ)'=/(х)
.
2°.
ІҐ(х)сІх = Дх)
+
С.
3°.
Да/О)+ /?£(*)]
ах =
а
^/(х)йх +р^%(х)ах
, а =
сопзі
і
Р =
сопзі
(ця
властивість називається властивістю лінійності інтеграла).
4°.Якщо \/(х)сіх
= Р'(х)
+
С та и = ср(х) , то
\/(и)<іи
= Р(и)
+
С.
Властивість
4
означає
, що
вигляд формули інтегрування
не
залежить
від того
, чи є
змінна інтегрування незалежною змінною
, чи
диференційов-
ною функцією
.
Обчислення невизначеного інтеграла
за
допомогою таблиці основних
інтегралів
та
його властивостей називають безпосереднім інтегруванням
.
Приклад
1.
Знайти інтеграли
:
гЗ
х
3
-^х
+ \ , „
г
(1 + 2х
2
) , . г 1 .
а)
сіх ; б) ф- сіх ; в) — ^~ ах .
-V
і
х
2
(\
+
х
1
) 'зіп .хсоз^х
Розв'язання
.
а)
|3х
3
-7х"
+
1
йх =
^
х
г
ах
_^
х
Л
(іх+
^ =
х
1-
2
4х~
+
\п\х\
+
С ;
г 0 + 2х ) , Л\л-Х ) + Х . еСІХ (• СІХ 1 _
х
2
(1 ьх
2
)
1
х
2
(1+х
2
)
}
х
2
Ч + х
2
х
\
Г
1
^
Г
8ІП
2
Х
+ С05
2
Х (• 1
г
1
В)
і
-
~
7~
(ІХ=:
\
2 Т
-
^
Х=
і 2~I 2~^
Х
=
ЗІП'хСОЗ X 81П Х-СОЗ X СОЗ X ЗІП X
=
г§х-сг§х
+ С .
150
