Тевяшев А.Д., Литвин О.Г. Вища математика. Загальний курс: Збірник задач та вправ
Подождите немного. Документ загружается.


їх +
1
, х<1 ;
3.40. Нехай Дх) =
2
[З - ах , х > 1.
За умовою якого вибору числа а функція /(х) буде неперервною
0
"обудувати її графік .
У задачах 3.41 -3.44 дослідити , в яких точках і якого роду мають розрив
лані функції:
і лх 1 1 л*>
51ПХ
3.41.
у = . 3.42. у
=
.
(х + 2)
2
х
, СОЗХ - . .
1
3.43.
у = . 3.44. у = г- .
х і
1+2*
5.45.
Довести , шо функції ^4-х -2 і х є нескінченно малими одного по-
рядку при х -» 0 .
3.46. Довести еквівалентність нескінченно малих функцій
1п (1
+ 5х) і е
5х
-1
при х-^0 .
3.47. Довести рівності при х -» 0 :
х агсзіп Зх = о(х) : 2х +хІ§2х = о(х) .
У задачах 3.48-3.81 продиференціювати дані функції:
3.48. у = (х
2
-Зх + 3)(х
2
+2х + 1). 3.49. у = (х + 1)
2
(х-1).
Х +
1
X
3.50. у = -. 3.51. у
=
—
х
2
+1
3.52.
у =
(1
-2х^)
4
. 3.53. у = Уі-х
2
.
3.54.
у = соз
2
х
•
3.55. у = Ззіп
2
х-зіп
3
х •
3.56. у = ЗІП х
3
• 3.57. у = 5ІП(С05Х
2
) •
д/і + х
2
3.58. у = 4 зіп(3х + 5). 3.59. У = зіп
3.60. у = (агсзіп х) 3.61. У = агсі§х .
-• ™ і 2 1 _ „ агсзіп х
3.62.
у = агсі£ -. 3.63. у =
•
111

3.64.
У =
1п
2
X.
3.65.
у
=
І0£
3
(Х
2
-1).
3.66.
У =
х
2
1о§з X .
3.67. У
= х-10
х
.
3.68.
У =
х
-
е
х
•
3.69. у
= е
х
СОЗ X .
3.70.
У^
3.71.
У
= ю
2
*-
3
3.72.
У =
хУ°
3
*.
3.73.
у
= зЬ
3
х.
3.74.
У =
1п
сЬ х.
3.75.
У
= е
с1
1
2
л-
3.76.
У =
х
х
\
3.77. у
= (!пх)
х
.
3.78.
У =
(зіп
х)
с05х
.
3.79. .У
3
2
-
.V
<••"' зіп 2х
3.80.
У =
^х
+
4х .
3.81.
У
- 2 - 3
=
8111
X ЗІП X
У задачах 3.82 - 3.85 знайти похідні від функції у, що задана неявно :
3.82. х
3
+у
3
-3аху = 0. 3.83. у
3
-Зу
+
2ах
=-
0 .
3.84. у = соз(х + у). 3.85. у =
1
+ х е
у
.
сіу
У задачах 3.86 - 3.88 знайти похідні — від функцій , що задані
параметрично
Заі
х
-
3.86.
Г
=
1 +
'з
:
3.87. Н"^^ 3.88. і
Х
:ї'
[у =
1
+
1
. [у = і-шсщі . у
=
+і
3
'
У задачах 3.89 - 3.91 знайти диференціал функції:
7 •> V
3.89. у = \
+ х
-х
2
. 3.90. у = Щ~х. 3.91.у = 2
/со
«.
3.92. у = (х т 10)
6
; у" = ? 3.93. /(*) = х
6
- 4х
3
+ 4 ; /
4
(1) = ?
3.94. /(х) =
<?
2
*
-1
;
/*(0) = ? 3.95. >- = 0 + х
2
)агсі§х : у" = ?
3.96. 6
2
х
2
+ а
2
у
2
= а V ; ^ = ? 3.97. у = зіп(х + у) ; у" = ?
йх^
112

3.98.
\х = асо5І ;
[у = а5ІпІ ,
ах
1
3.99.
|х = а соз і ; Д" у
[у = азіп
2
/ , сіх
2
3.100. у = Чх
2
; сі
2
у = 1
У задачах 3.101 - 3.109 знайти границю функції, використовуючи
правило Лопиталя:
3.101.
Ііт Л=
ТІЇ ,— ,— -
3.103.
Ііт
е
ах
-
совах
3.102.
Ііт
Іп созх
3.104. Ііт
.г->0 X
Іп
зіп 2х
х~>0 ІП51ПХ
3.105. Ііт х
х->0
1п(е
Т
-1)
3.107. Ііт
хзіп —
.
,г->со X
3.106. Ііт
сг§х—
І
.
л--»0 І, X )
3.108. Ііт
х->1
х-1 Іпх
3.109. Ііт (е
х
+х)
х
.
х->0
У задачах 3.110 - 3.114 провести повне дослідження функцій і
накреслити графіки :
3.110. у =
3.111.
у =
-
1
3.113.
у = (х
2
-І)-
5
. 3.114. у
1-х'
х
3.112.
У
:
3.115. Знайти кутовий коефіцієнт дотичної, проведеної до параболи
у = х
2
•
1) на початку координат ; 2) у точці (3, 9); 3) у точці (-2, 4); 4) у
точках перетину її з прямою у = Зх - 2 .
3.116. Написати рівняння дотичної і нормалі, проведених до кривої
у = я-
3
у точці з абсцисою 2 .
У задачах 3.117 - 3.121 знайти частинні похідні даних функцій за
кожною з незалежних змінних :
113

3.117. 2 = (5х
2
у-у
3
+7)
3
. 3.118. 2 = агсі§- .
У
3.119. г = \п(х
+
^х
2
+у
2
) . 3.120. 2 = 1п(х
2
+у
2
) .
х
3.121.
2 = е * .
У задачах 3.122 - 3.125 знайти повні диференціали даних функцій :
3.122. 2 = х
2
у
4
3.123. 2=Діп (х
2
4-у
2
) .
3.124. 2 = агсзіп— . 3.125. 2 = зіп (ху) .
У
3.126. и =
е
х
~
2у
, х = $тг, у = 1
3
; — = ?
А
3.127. м = х
2
+у
2
+гу , у-е'. / = зіп/; — = ?
Ж
2.
М „ ~
<?
2 „
<?
2 „
3.128. - =* Іпу. * = -, у = 3м-2у; = ? = ?
3.129. 2 = х у-у х, Х =
ИСОЗУ,
у = и$іпу;
——
= ?
——
= ?
V
ау
УзадачахЗ.130-3.ІЗЗзнайти похідну — від функцій , заданих неявно
вказаними рівняннями :
3.130. х
3
у-у
3
х = а
4
. 3.131. х
2
у
2
-х
4
-у
4
= а
4
.
3.132. уе
х
+е
у
=0 . 3.133. ху-1пу = а >
2
-
г?
2
2 г?
2
'
У задачах 3.134 - 3.137 знайти —, і від даних
дх
2
дхду ду
1
-
функцій:
4
3.134.
Ї=-УІ(х
2
4-у
2
)
3
. 3.135. 2 = зіп
2
(ах
+
Ьу) .
3.136. : = \п(х +
4х
2
4-у
2
)
. 3.137. 2 = у
1п де
114

У задачах 3.138-3.141 знайти точки екстремуму функцій :
3.138. г = 2ху-3х
2
-2у
2
+10 .
3.140. : = х
2
+ху
+
у
2
+х-у
+ ]
.
3.139. : = Цх-у)-х
2
-у
2
3.141.
г = х
3
+
у
3
-Зху
.
У задачах 3.142 - 3.144 знайти умовні екстремуми функцій :
3.142. г=ху при х + у-\ .
3.143.
2 = х + 2у при
3.144. 2 =
—
+
—
при
х у
х
2
+у
2
= 5 .
х
+
у
=
2
3.6. І/Індивідуальне завдання З
Задача
1.Знайти
граниш функцій .
Варіанти завдань
а) Ііт
2х
3
-Зх
+
1
х-»» 4 + 2х
2
-
Зх
3
б) Ііт
-2х-3
х->3 х - 5х
+
6
в) Ііт
-Ух-2
х
->4 х-4
Х&Х-51П
X
г) Ііт
х->0
д) Ііт
X—»«
3.
а) Ііт
х
X
І
X—»0О
' і
1
+
Х,
6х
2
+5х-4
х->«> Зх -5х + 1
б) Ііт
4х
3
-2х
2
+х
х-»0
Зх +2х
2.
а) Ііт
Зх
4
-х
2
+4
дг-ю>5х
4
+4х
2
+1
б) Ііт-
х
£
-ЗХ
+
2
х-*\
х^ -4х + 3
2 + х
в) Ііт ,
х->-2 1-л/х +
З
г) Ііт
х->0
5Іп(я + х)-5іп(а-х)
Д) Ііт 1+-
\->со
\ X
Зх
4.
а) Ііт
х
5
+3х
2
+5
х
3
-1
б) Ііт
х
2
+3х-10
х->2
Зх" -5х-2
115
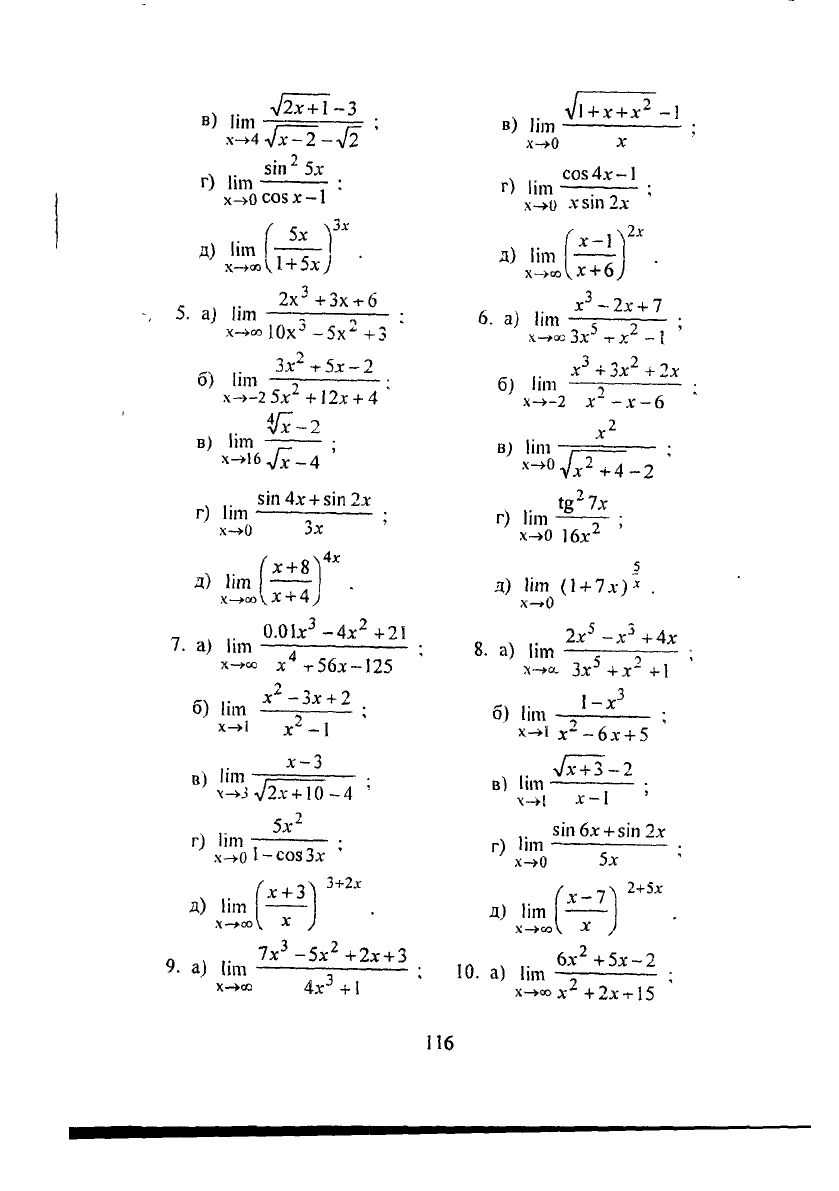
, ,. л/2лг + 1~3
в) Ііт -р=—=
х->4
л/х-2 -л/2
. . зіп
2
5х
г) Іип :
х->о
созх-1
( 5х V
і
'
Д) Ііт і ——
Х-*ооЧІ
+ 5х )
5.
а] Ііт
2х" +3х-і-6
х->» Шх'
3
-5х^ +3
б) Ііт
Зх~
2
5х
2
+ 12х + 4
в) Ііт
Гх-г
х
-»
16
л/х-4 '
5іп4х + зіп2х
г) Ііт
х-+0
^x
..З ...2
х-*«Лх
+ 4 /
О.ОІх
3
-4x^+21
7.
а) Ііт .
*->•«> х т56х-І25
~ .. х
2
-Зх + 2
о) Ііт ;
х->1
х
2_!
а) Ііт
х-3
ПШ
, •
\->іл/2х + 10-4 '
.2
г) Ііт
5х'
х-^.о1-созЗх '
д) Ііт
Х-*оО
9. а) Ііт
3+2.Ї
х + 3'
7х
3
-5х
2
+2х + 3
4х
3
+1
в) Ііт
х->0
г) Ііт
Уі + х+х
2
-1
х
соз 4х-1
х-м)
хзіп2х
д) ііт
6. а) Ііт
•ах
—У
х
3
-2х + 7
5 т '
х->« .зх
-г
х - І
,. х
3
+3х
2
+2х
б) Ііт ^
х-»-2 х~-х-6
в) Ііт
х->0
г) Ііт
18 ~7х
+ 4 -2
х->0 16х'
д) Ііт
(1
+ 7х)
х
х-*0
8. а) Ііт
2х
5
-х
3
+4х
х~*^ Зх
5
+х
2
+1
б) Ііт —
1-х
х->і
х~ -6х + 5
ч
,. л/х + 3-2
в) Ііт
Х-Й х-1
г) Ііт
х->0
зіп бх + зіп 2х
5х
д) Ііт
х->«Л
х
2+5х
Ю.
а) Ііт
6х
2
+5х~2
х-»со
х
*
+2х-г15
116

б) Ііт
х-2
х->2х^
-Зх + 2
42-42-х
в) Ііт т
х-й)
2х
г) Ііт
.
я
зіп" х
х->0 5х зіп 2х
д) Ііт
х->»
зx^
б) Ііт —
х
2
-9
х->3х~ -2х-3
л/і +
х-4\-х
в) Ііт
х->0
х
1
- соз х
г) Ііт г—
х-*0
7х
2
ч
..
(2х-1)
д) Ііт г—г
2дг
II.
а) Ііт
4х -Зх+5
х->°°
-0,1х
ч
+2х-1
х
2
-х-2
б) Ііт : •
х->-1 X
і
+1
,.
Тх-1
в)
1іт
,~г~7
;
Х-»І ^ІХ -1
агсзіп(1-2х)
г) Ііт ^ ;
.1
4х" -1
12.
а) Ііт
1-4х
3
х->сю 2 + х + х
2
+ 8х
3
Зх + 6
б) Ііт —5
х-»-2х-*
+8
в) Ііт
х->0
1
+ х
2
-1
X
зіп 5х
г
) Ііт -7=— •
х->0 л/х +1 -1 '
Зх-2
д) Ііт
х
_>оо^3х
+ 1
2л:
13.
а) Ііт —,
5х
2
-Зх + 2
х->к>
2х і-4х + 1
б) Ііт
16х^-ІЗх-3
пні
2
х-и
2х +Зх-5
в) Ііт
х-+0
зх
зіпЗх
г) Ііт
х-»0%/х
+ 2 --У2
1-л
д
) Ііт (1-4х)
1
х-»0
,.
х
5
-3х
3
+ 12
14.
а) Інп г
х-><*
2х
5
+149
х
2
-2х
б) Ііт
—5
;
х->2х
-5х + 6
в) Ііт
х-»(
г) Пт
х->0л/і
+ 3х -1
агсзіпЗх
х->072-х
-л/2
117-
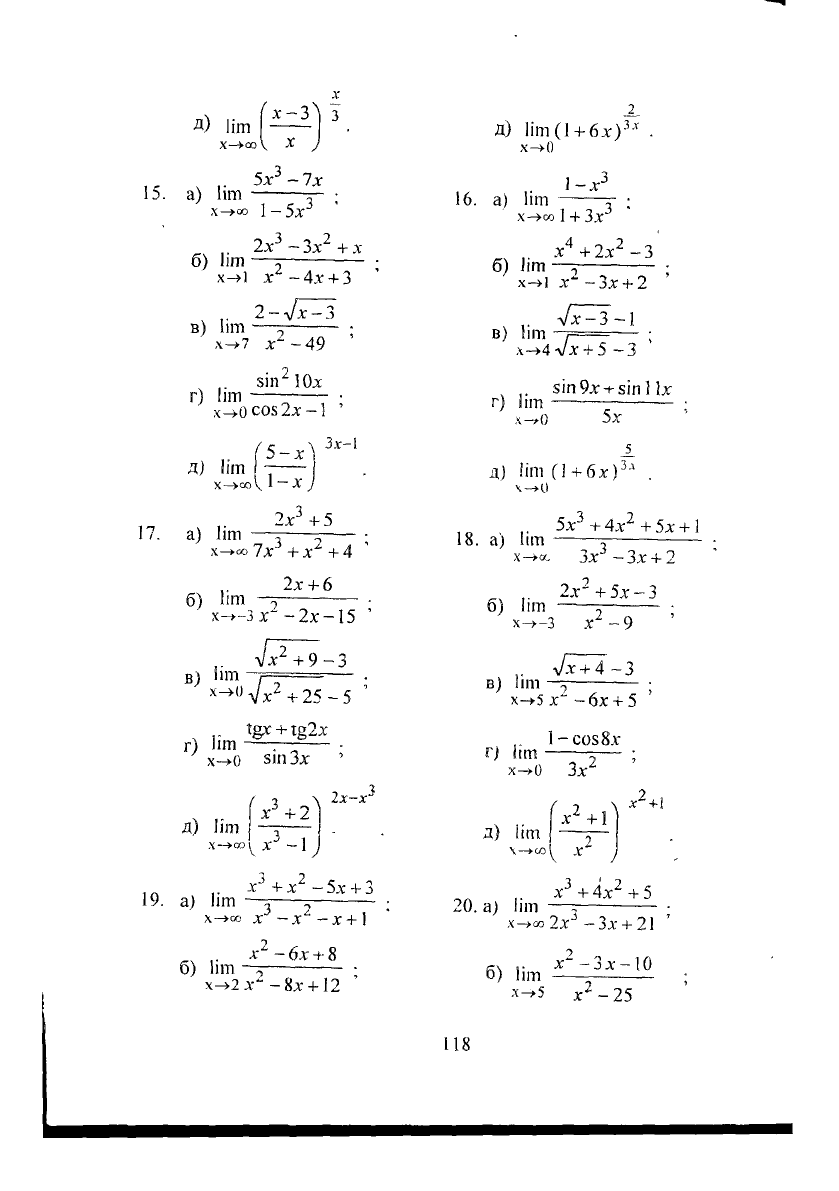
Д) Ііт
х-3)
з
Д) Ііт
(1
+ блг)
х-»0
,< ч г
5х 1х
15.
а) Ііт г-
х-х» 1-5х
б) Ііт
2х
3
-Зх
2
+х
х->і
х
2
- 4х +
З
'
в) Ііт —= •
х^7 х~~49 '
5іп 10л:
г)
Ііт • •
х
_>.0
соз2х -1 '
5-х
Д) Ііт .'
X—>сс\
1-Х
„з
Злг-1
2г
5
+5
17.
а) Ііт —~
х-><»
7х + х^ +4
2х + 6
б) Ііт — •
х->-з
х" -2х-15 '
,.
л/х^+Т-З
в)
Ііт-у- = .
х
^
(
Чх
2
+ 25-5
т§х + х§2х г) Ііт .
х->о
зіп Зх
д) Ііт
х
3
+2
2х-
Х-^сюу
X
—
1
19.
а) Ііт —
х
3
+ х
2
- 5х +
З
Х->оо
X -X -Х+ 1
б) Ііт
х -6х + 8
х->2х~
-8х + 12
.
1-х
3
16.
а) піп г-
Х-ЮОІ+ЗХ
х
4
+2х
2
-3
б) Ііт
х->і
х- - Зх
+
2
в) Ііт
X-»'
г) Ііт
.
л/х-3 -1
х->4 л/х + 5 - З
зіп9х-г-зіп1 їх
5х
_5_
\3Л
д) Ііт 0 + 6х)
3л
-
ч->0
18.
а) Ііт
5х
3
+ 4х
2
+ 5х +
1
х-«с
Зх
3
-3х + :
,.
2дг+5х-3
о) Ііт ^
х->-з
х - 9
,.
л/хТї-З
в) Ііт —5; ;
х-*5 х" -6х + 5
,.
1-соз8х
П Ііт =— ;
х^О Зх^
д) ііт | ,
\-><о^ х~
х
2
+1
х
2
+ 1
20.
а) Ііт
х
3
+4х
2
+5
*-><*>
2х
л
- Зх + 21
б) Ііт
х~
-Зх-10
*->5 х^-25
118

в) Ііт
х->0
г) Ііт
х-»0
1+х4-х
х + х
х
2
-х
созх
д) Ііт
Х-*ОО
21.
а) Ііт
х-3
х +
2
-2х + 17
х->С» 24х
3
4-0,24х-17
б) Ііт —2
х
2
+2х
х->~2х
+5х + 6
,
,
5-7x4-12
в) Ііт —^
х->із
х
2
-169
г) Ііт
„
х-»0
л/і +
Х5ІПХ
- 1
•їх -8
в) Ііт з7——
х->64
:
г) Ііт
х->0
^\
+
і%х-^\-щх
І
+
X
д) Ііт ! "
х—>ОО
V
.3 4- х
51ПХ
х
22.
а) Ііт
х
5
-3х
3
+1
Я
9 Ч
х-+аі
4х - х" + х
3-7?
+ х
Х^4
в) Ііт
-6x4-8
х-+4
х
2
- 5х + 4
г) Ііт
1-С05 х
х->0
Зх"
( 7x4-1
д) Ііт -
х-*ОО\
23.
а) Ііт
7х
0,1х
4
-х
3
+х
2
х-хи
2х
5
-6х
4
+5
б) Ііт
З/х-6 +2
х->-2
х + 8
УІХ-2-2
в) Ііт
х->6
г) Ііт
х-6
1
•сІ%х •
(х-6)
Ііт
Д) Пт ,
х->СО\
X 4-1
2х+3
24.
а) Ііт
5
2 п
X
4-Х 4-7
х->ОО 17
4-Зх"
5
х
2
-5x4-6
б) Ііт —^
х->2Г
-7x4-10
л/х-3 -1
в) Ііт
г) Ііт
х->4
л/х + 5 -
З
1-л/созх
х
->о
8хзіпх
д) Ііт
X—«О
2х
2
+3
Зх'
2х* + \)
Ц.)
Ііт
Х-»СО
{\+9х)
5х
119
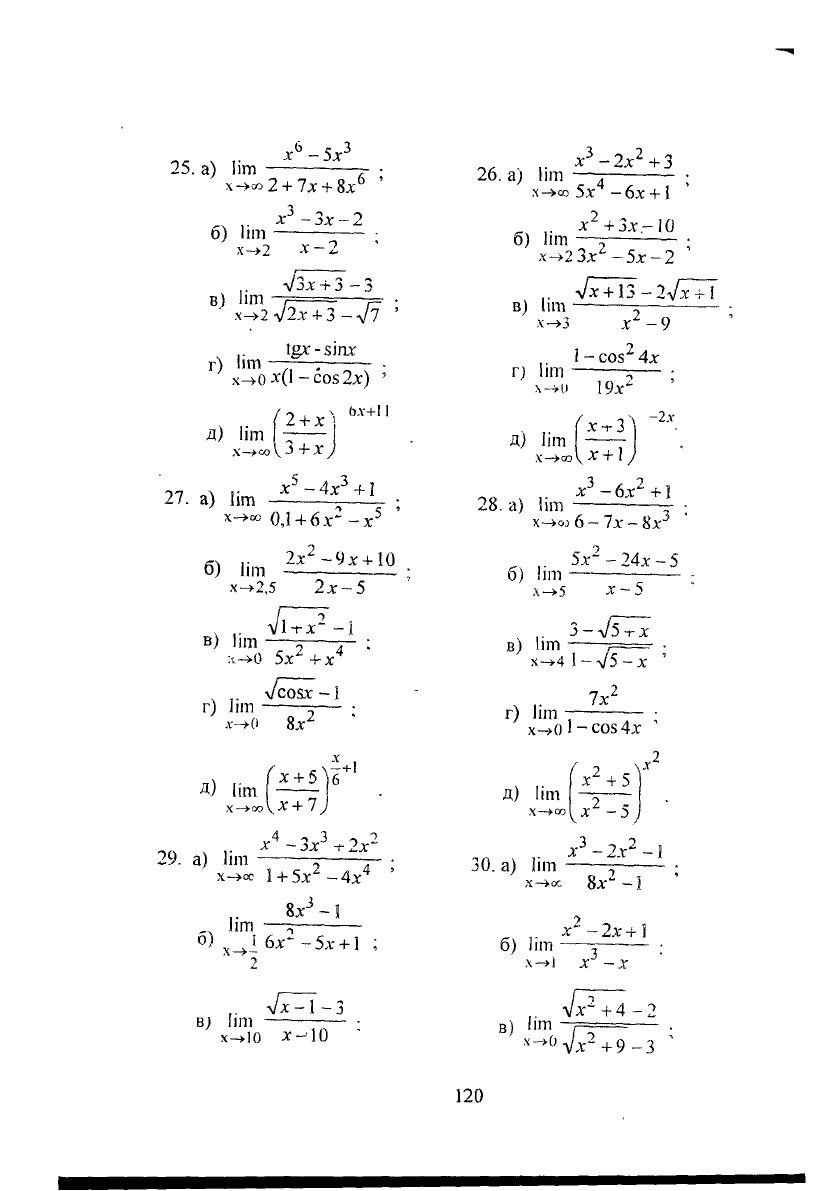
25.
а) Ііт
х
6
-5х
3
хч><»2
+ 7х + 8х
6
б) Ііт
х
3
-Зх-2
х->2
X -
в) Ііт —
у/3>
зх
+
з -
З
х^2
л/2х +
3
- л/7
Іах-зіпх
г) Ііт —~ -
х->0*(1-СО!5
2х) '
д) Ііт -
2
+
х)
Ь.ї+1
і
Х—>оо '
27.
а) Ііт
х
5
- 4х
3
+1
0,1
+ 6х
2
-х
5
б) Ііт
х->2,5
2х~5
в) Ііт
•х
2
-1
-»0
5х
2
+ х
4
ч
,. 7с05Х-1
г) Ііт -=—
х->0
%Х
£
Д) Ііт і і
х—>со
V
X + 7)
+ 1
,0
, г ^-Зх
3
.2х
2
29.
а) Ііт —= —
х->ос
1
+
5х
2
-4х
4
8х
3
~1
„ пт —,
о) і 6х'-5х +
1
;
в;
Ііт
7х^Т-з
х->10
х-іО
26.
а) Ііт
х
3
-2х
2
+3
х->ео
5х
4
- 6х + 1
х
2
+3х.-10
х-*2
Зх
2
- 5х - 2
б) Ііт
в) Ііт
О Ііт
Ух+
13
-2л/л
х
2
-9
1-соз
2
4х
х->о
19х
А
д) Ііт
Х-гЗ
Х-*оо
V.
X + 1
-2.Г
28.
а) ііт
х
3
- 6х
2
+1
х-><н
6 - 7х - 8х
3
5х
2
-24х-5
б) Ііт —
х->5
*-5
в) Ііт
З-л/5-
х->4
1- 4Ь~.
г) Ііт
7х
2
ЗО.
а) Ііт
х
_>0
1
-со5
4х
1
х~ + 5
х
2
-5
-
/
х
3
-2х
2
-1
д) Ііт
X—»со
х-*«
8х"~]
б) Ііт
х- -2х +
1
Х->1
X -X
,
•\/х
2
+4-2
х
^°\/х
2
+9-3
120
