Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3
Подождите немного. Документ загружается.


§
1.
Диференціальні рівняння першого порядку
61
1.62. (у
+
л]х
2
+у
2
)ах-хс1у = 0; у(\) = 0.
Розв'язати задані геометричні задачі, що зводяться до ди-
ференціальних рівнянь, однорідних відносно змінних.
1.63. Знайти лінію, у якої квадрат довжини відрізка, що
відтинається будь-якою дотичною від осі ординат, дорівнює до-
бутку координат точки дотику.
1.64. Знайти лінію, у якої початкова ордината (ордината при
х = 0) будь-якої дотичної дорівнює відповідній піднормалі.
1.65. Знайти лінію, у якої довжина полярного радіуса будь-
якої її точки М дорівнює відстані між точкою перетину з віссю
Оу дотичної, проведеної в точці М, і початком координат.
1.66. Знайти криву, якщо в кожній її точці довжина відріз-
ка дотичної дорівнює довжині відрізка, який відтинає дотична
на осі Ох.
1.67. Знайти криву, дотична до якої в довільній точці від-
тинає на осі ординат відрізок, рівний абсцисі точки дотику.
1.68. Знайти криву, для якої добуток абсциси будь-якої точ-
ки,
що належить кривій, на відрізок, що відтинається нормаллю
на осі Ох, дорівнює подвоєному квадрату відстані цієї точки
від початку координат.
Лінійні диференціальні рівняння та звідні до них
У задачах 1.69 - 1.81 розв'язати задані лінійні диферен-
ціальні рівняння першого порядку.
1.69. /
+
2у = 4х.
1.71. у'
+
2ху = хе'
1.70. у'
+
2у = е
_ / 1 2х .
1.72. у
+——у
= 1
х
1.73.
(1
+ х
2
)/-2ху = (1 +
л:
2
)
2
.
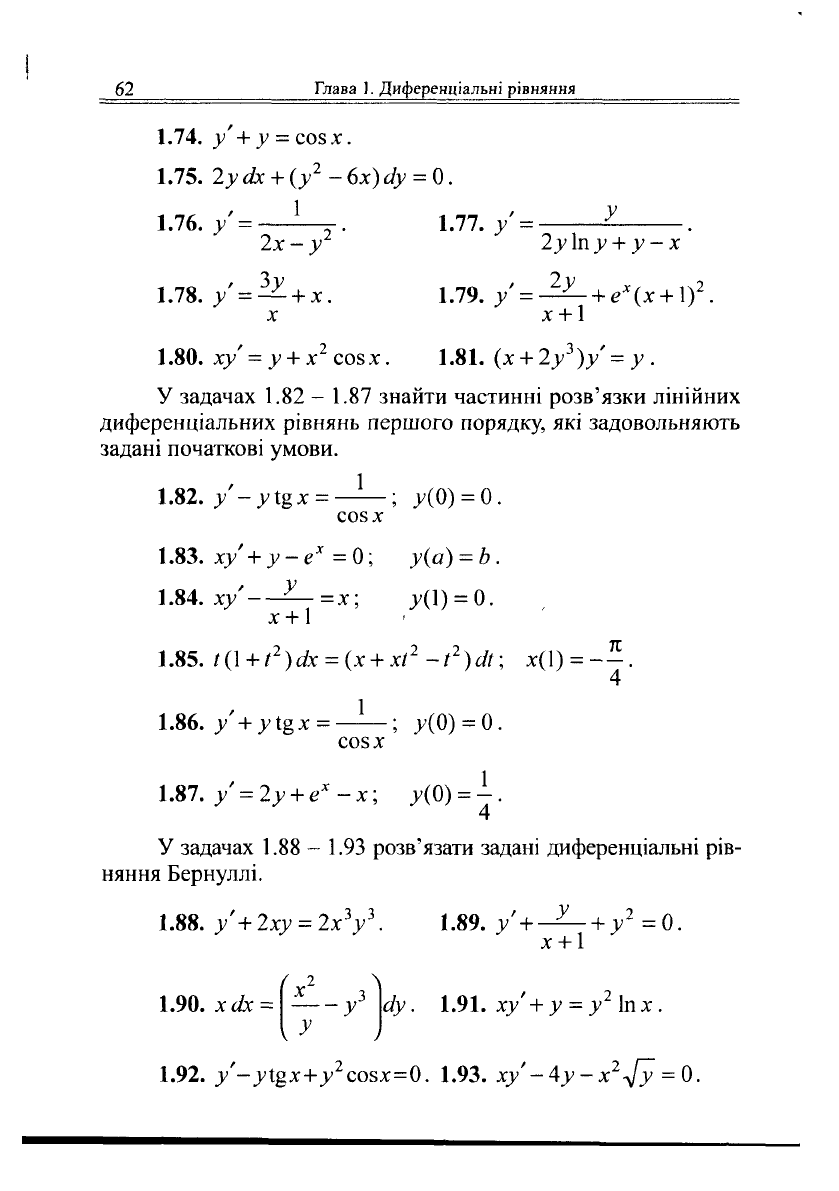
62
Глава 1. Диференціальні рівняння
1.74. у + у = С05Х.
1.75. 2у ах + {у
2
- 6х) ду = О.
1.76. у'
1
2х-у
2
1.78. / = ^ + х.
х
1.77. / =
У
1.79. у
2у\пу + у-х
'
2
У , , ,4.2
Х +
1
+ е
х
(х + \у.
1.80. ху' - у + х
2
созх. 1.81. (х + 2_у
3
)
і
у' = у .
У задачах 1.82 - 1.87 знайти частинні розв'язки лінійних
диференціальних рівнянь першого порядку, які задовольняють
задані початкові умови.
1.82.
у'-
уХ%
х
= — \
У(0)
= 0.
созх
1.83. ху'
+
у-е
х
= 0; у(а) = Ь.
1.84.x/
—=х; у(\) = 0.
х +
1
1.85. і(\ +
(
2
)сіх
= (х + х(
2
-1
2
)д(;
х(1) = --.
4
1.86. у'
+
у
і&Х
= -}—; у(0) = 0.
созх
1.87. у=2у + е
х
-х; у(0) = -.
У задачах 1.88- 1.93 розв'язати задані диференціальні рів-
няння Бернуллі.
1.88.
/+2ху = 2хУ. 1.89. у'+^— + у
2
= 0.
х +
1
1.90. хдх =
х
у"
ду. 1.91. ху'+ у = у Іпх.
1.92. у'-уЩх+у
2
сокх=0. 1.93. ху'
-Ау-х
2
4у
= 0.

§
1.
Диференціальні рівняння першого порядку
63
У задачах 1.94 - 1.96 знайти частинні розв'язки рівнянь Бер-
нуллі першого порядку, які задовольняють задані початкові умови.
1.94. Зсіу = -(І + Зу
2
)у
5іпхсіх
; у |=1.
1.95. усіх-
( \ г\
х х у
2
=
і
1.96. у'-уі&х
+
у
2
созх = 0 ; у(0) = 1.
1.97. Розв'язати задане рівняння Ріккаті при заданому час-
тинному розв'язку у,(х) цього рівняння:
а) (\ + х
2
)у'+2
]
-^у + 3 = у
2
,
Уі
(х) = -;
X
X
'
2 У З
б) у + ху н—-х +2,
у
]
(х)-х;
X
в) X
і
у -у
2
-х
2
у = -х
2
, у
]
(х) = х;
г)у-у — = -т, .УіО) =—;
XX
X
д) ху -
3
у + у" = 4х -4х, _У|(х) = 2х;
е) (х-х
4
)у'-х
2
-у + 2ху
2
=0, у,(х) = х
2
.
Розв'язати задані геометричні та фізичні задачі, що зво-
дяться до лінійних диференціальних рівнянь першого порядку
та до рівнянь Бернуллі.
1.98. Знайти лінію, у якої початкова ордината (ордината
при х = 0) будь-якої дотичної на дві одиниці масштабу менше
абсциси точки дотику.
1.99. Знайти криві, для яких площа трикутника, утворено-
го віссю Ох , дотичною і радіусом-вектором точки дотику, є ве-
личиною сталою і дорівнює а
2
.
1.100. Площа трапеції, утвореної дотичною до деякої кри-
вої, осями координат та ординатою точки дотику, є сталою ве-
личиною та дорівнює а
2
. Знайти цю криву.

64
Глава 1, Диференціальні рівняння
1.101. Знайти криву, кожна дотична до якої перетинає пря-
му у =
1
у точці з абсцисою, що дорівнює подвоєній абсцисі
точки дотику.
1.102. Знайти криву, дотична до якої в точці М(х,у) про-
ходить через точку /^(х
2
, у
2
) .
1.103. На тіло маси т, яке рухається прямолінійно, діє
сила, пропорційна часу, що проходить від моменту, коли швид-
кість дорівнювала нулю, та сила опору, яка пропорційна швид-
кості. Знайти залежність швидкості від часу, якщо коефіцієнти
пропорційності відповідно дорівнюють к
(
та к
2
•
1.104. На тіло маси т , яке рухається прямолінійно, діє сила,
пропорційна кубу часу, що проходить від моменту, коли швид-
кість дорівнювала
У
0
,
та сила опору, яка пропорційна добутку
швидкості та часу. Знайти залежність швидкості від часу, якщо
коефіцієнти пропорційності відповідно дорівнюють та к
2
•
1.105. Сила струму / в електричному колі з опором К і кое-
фіцієнтом самоіндукції Ь задовольняє рівнянню
Ь
— -\-КІ = Е,
сії
де Е - електрорушійна сила. Знайти залежність сили струму /(/)
від часу, якщо Е = £
0
зіп
Ш
і /(0) = 0.
1.106. Початкова температура тіла 0
О
дорівнює темпера-
турі навколишнього середовища. Тіло дістає теплоту від нагрі-
вача зі швидкістю сф(7), де с - стала теплоємкість тіла і віддає
теплоту навколишньому середовищу зі швидкістю охолоджен-
ня,
яка пропорційна різниці між температурами тіла і середови-
ща. Знайти залежність температури тіла від часу, який відрахо-
вується з моменту початку досліду.
Диференціальні рівняння у повних диференціалах та
звідні до них
У задачах 1.107 - 1.114 розв'язати задані диференціальні
рівняння, попередньо впевнившись, що вони є рівняннями у
повних диференціалах.

§1,
Диференціальні рівняння першого порядку
65
1.107.
(2х
3
-ху
2
)ах
+ (2у
3
-х
2
у)сіу
= 0.
1.108.
с
3
хсіу
х
т
77
У
2
2
х
1
+
у
1
-1
СІХ
.
)
1.109.
е
у
ах
+ (хе
у
-2у)сіу
= 0.
1.110. ух
у
~
[
ах
+
х
у
\пхсіу
= 0.
хсіх
+
усіу
у
сіх-хсіу
1.111.
4^7
1.112.
> +
5ІП
"
С
°
8
(х
^
+
-
•ау
+
зіп
у ау - 0.
СОЗ
(ху) СОЗ (ху)
1.113.
(1
+
хд/х
2
+
у
2
)йх
+ (-1 +
Л
/*
2
+У
2
)У^У
= 0.
.
2х<&
у
2
-Зх
2
,
А
1.114.
—— + - - ф = 0.
У
У
У задачах
1.115-1.121
знайти розв'язки заданих диферен-
ціальних рівнянь, використовуючи інтегрувальний множник.
1.115.
(х
2
+у)сіх
-
хсіу
= 0.
1.116.
у (\ + ху)
сіх
- х
сіу
= 0.
1.117.
(х
2
+ у
2
+2х)сіх
+
2усіу =
0 .
1.118.
^сіх +
(у
г
-1пх)ф
= 0.
X
1.119.
(х
С05
у - у
$іп
у)
сіу
+ (х
§'т
у + у
соз
у)
сіх
= 0.
1.120.
(х +
у
2
)сіх-2хусіу
= 0.
1.121.
у
(1
+
ху)ах
- хф = 0 .
1.122. Впевнитись,
що
інтегрувальним множником ліній-
ного рівняння
у'+ Р(х)у = /(х) є
функція
ц(х) =
1.123. Знайти інтегрувальний множник рівняння Бернуллі
у'+Р(х)у
=
у"/(х).

66
Глава І. Диференціальні рівняння
Диференціальні рівняння, нерозв'язні відносно
похідної
У задачах 1.124 - 1.130 розв'язати задані диференціальні
рівняння, нерозв'язні відносно похідної.
1.124. у =
у'
2
+4у'\
1.125. у = (у'-\)е
у
'.
'2
1.126. у = ^
+
2ху'+х
2
. 1.127. х =
у'
3
-у'+2.
1.128. х =
у'со$у'.
1.129. х = 2у'-\пу'.
1.130.
х=Л
+ 4
У у'
2
У задачах 1.131 - 1.141 знайти загальні та особливі роз-
в'язки заданих рівнянь Лагранжа та Клеро.
'З
1.131. у = ху'+ у'
2
. 1.132. у - ху'- Зу
1.133. у = ху'
+
—,. 1.134. у = ху'+л]\ + у'
2
.
У
1.135. ху - у-
1п
у . 1.136. у = у'
2
(х
+ 1) .
1.137. 2уу = х(у'
2
+ 4). 1.138. у = уу'
2
+2ху'.
1.139. у = х(\ + у') + у'
2
. 1.140. у'
=
\п(ху'-у).
1.141. у = у\х + \) + у'
2
.
Розв'язати задані геометричні задачі, що зводяться до ди-
ференціальних рівнянь, нерозв'язних відносно похідної.
1.142. Знайти лінію, дотичні до якої відтинають на осях
координат відрізки, сума яких дорівнює 2а.
1.143. Знайти лінію, для якої добуток відстаней довільної
дотичної до двох заданих точок є величина стала.
1.144. Знайти лінію, якщо відрізок довільної її дотичної,
яка лежить між осями координат, має сталу довжину а.

§1.
Диференціальні рівняння першого порядку
67
1.145. Площа трикутника, утвореного дотичною до шука-
інії
і
ОСЯІУ
ти цю лінію.
ної лінії
і
осями координат, є величина стала
і
дорівнює а
2
. Знай-
Ортогональні траєкторії
У задачах
1.146-1.149
знайти траєкторії, ортогональні за-
даним сім'ям кривих (а - параметр).
1.146. Параболам
а)у = сгх
2
; б) у
2
- 4(х - а).
1.147. Колам х
2
+ у
2
= 2ах .
1.148. Гіперболам х
2
-2у
2
= а
2
.
1.149. Кривим
а) ау
2
= х
3
; б) у = ае
2х
.
Різні типи диференціальних рівнянь першого порядку
У задачах
1.150-
1.159 визначити типи заданих диферен-
ціальних рівнянь і вказати у загальному вигляді підстановки або
методи їх розв'язання.
у-хг
1.150. зіпх
3
- е
у
.
1.151.
1
+ х +
(1
+ х
2
)(е
х
-
е
2у
у)
= 0 .
1.152. 2/(1 - X
і
) - ху - 2ху
2
+ 2х
г
у
2
= 0.
1.153. усІх + (2х-у
2
)сІу = 0.
( х
2
^
1.154. х + у шх+ 2ху + у
[у ) {
2
У )
1.155. усіх + (х - 2л[ху )сіу = 0 .
1.156. (х
2
+ у
2
+ ])сіу + хусіх = 0.
1.157.
у' =
8Іп(_у
- х).
* «СЕ у - а
1.158. х =
&гссо?>-
.
У
сіу = 0.

68
Глава
І.
Диференціальні рівняння
х
2
+ 2х -1
У задачах 1.160
- 1.186
знайти загальні розв'язки заданих
диференціальних рівнянь.
1.160.
/ =
1.162.
у
х + у-2
у-х-4
а
2
(х + у)
2
'
1.161.
у
,
у
2
+ ху - х
2
У
1.163.
у {у
2
-х) =
у.
.
...
2хсіх
у
2
-Зх
2
.
1.164.
—г~
+
з—сіу
= 0.
У У
1.165.
(2у + ху
л
)сЬс + (х + х
2
у
2
)сїу = 0.
1.166.
2ху +
х у +
У
з \
сіх + (х~ + у )сіу = 0.
_
0 +
1.167.
у =
х(у + \)-х'
1.168.
хсіу + у сіх + у
2
(х сіу - у сіх) - 0.
1.169.
іи-д')
У)
еіу = 0.
1.170.
у'
= хі[у +
ху
х
2
-
1.171.
,у5Іпх
+.у'созх
= 1.
1.172.
у'-у
+
у
2
созх
= 0.
,
/
созхзіпу-Ие
2
х
1.173.
_у =
:
2
—.
5ІПХСОЗ
г
у у
1.174.
Ху
СОЗ—
=
>'С08—
- X .

§1 Диференціальні рівняння першого порядку
69
1.175. [ ХС08—+ У5ІП —
усіх +
( у у \
хсо8—
-узіп— хсіу
=
0.
1.176. у' = -
СОЗу
' 2 •
1.177. у-у
С08
х = у
008
х(1
-
81П
х).
2 2
* +> 2 , 2
\ЛЖ2уу' = е * + - ^—2х.
1.179. (і +
^')л
+ е*
Л
'| 1-- |ф = 0
7
З
1.180.
(х
2
-\)
2
сіу
+
(х
г
+ 3хул]х
2
-1)ах = 0.
1.181. \%х^—у = а.
сіх
1.182. ху/
2
-(х
2
+/)/ + ху = 0.
1.183. (Зх
2
+2ху-у
2
)сіх + (х
2
-2ху-3у
2
)сіу = 0 .
1.184. х/ = х
2
^' + 2.
1.185. (2хе
у
+ у
4
)у'
=
уе
у
.
1.186. у =
/
2
+2х/+у.
Розв'язати задані геометричні та фізичні задачі.
1.187. Знайти лінію, у якої довжина нормалі пропорційна
квадрату ординати. Коефіцієнт пропорційності дорівнює к .
1.188. Знайти лінію, у якої будь-яка дотична перетинаєть-
ся з віссю ординат у точці, однаково віддаленій від точки доти-
ку і від початку координат.
1.189. Знайти рівняння лінії, яка перетинає вісь абсцис у
точці х =
1
і такої, що має властивість: довжина піднормалі в
кожній точці лінії дорівнює середньому арифметичному коор-
динат цієї точки.

70
Глава І. Диференціальні рівняння
1.190. Знайти лінію, у якої площа трапеції, утвореної ося-
ми координат, ординатою довільної точки і дотичної в цій точ-
ці,
дорівнює половині квадрата абсциси.
1.191. Знайти рівняння кривої, яка проходить через точку
(л/2 ,0) , якщо сума довжини її дотичної та піддотичної дорів-
нює добутку координат точки дотику.
1.192. Знайти рівняння кривої, яка проходить через точку
(1,2),
якщо її піддотична вдвічі більше абсциси точки дотику.
1.193. Знайти рівняння кривої, яка проходить через точку
,-1 ^, якщо довжина відрізка півосі абсцис, що відтинається
її дотичною, дорівнює квадрату абсциси точки дотику.
1.194. Знайти рівняння кривої, яка проходить через точку
(1,0),
якщо довжина відрізка осі абсцис, що відтинається її нор-
маллю, на дві одиниці більше абсциси точки дотику.
1.195. Знайти лінію, у якої піднормаль в будь-якій точці
так відноситься до суми абсциси та ординати, як ордината цієї
точки до її абсциси.
1.196. За який час температура тіла, яке нагріте до 100° С,
зменшиться до 25° С, якщо температура приміщення дорівнює
20° С і за перші 10 хвилин тіло охолодилося до 60° С?
1.197. Швидкість розпаду радія пропорційна його кількості.
Протягом року із кожного грама радія розпадається 0,44 мг. Через
скільки років розпадеться половина наявної кількості радія?
1.198. Човен уповільнює свій рух під дією опору води,
який пропорційний швидкості човна. Початкова швидкість
човна 1,5 м/с, швидкість її через 4с 1 м/с. Коли швидкість змен-
шиться до 1 м/с? Який шлях пройде човен до зупинки?
1.199. Пуля, яка рухається зі швидкістю
У
0
= 400 м/с, проби-
ває стіну товщиною п = 20 см і вилітає, маючи швидкість 100 м/с.
Покладаючи силу опору стіни пропорційною квадрату швидкос-
ті руху пулі, знайти час проходження пулі крізь стіну.
