Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3

Подождите немного. Документ загружается.

Диференціальні рівняння першого порядку

У / У

кх- або у = —.

У кх

Інтегруючи, маємо сім'ю шуканих кривих:

Сх.<

Приклад 20. Знайти рівняння кривої, яка проходить через

точку (1,0), якщо відомо, що трикутник, утворений віссю Оу,

дотичною до кривої в довільній її точці і радіусом-вектором точ-

ки дотику, рівнобедрений, причому основою його є відрізок до-

тичної від точки дотику до осі Оу.

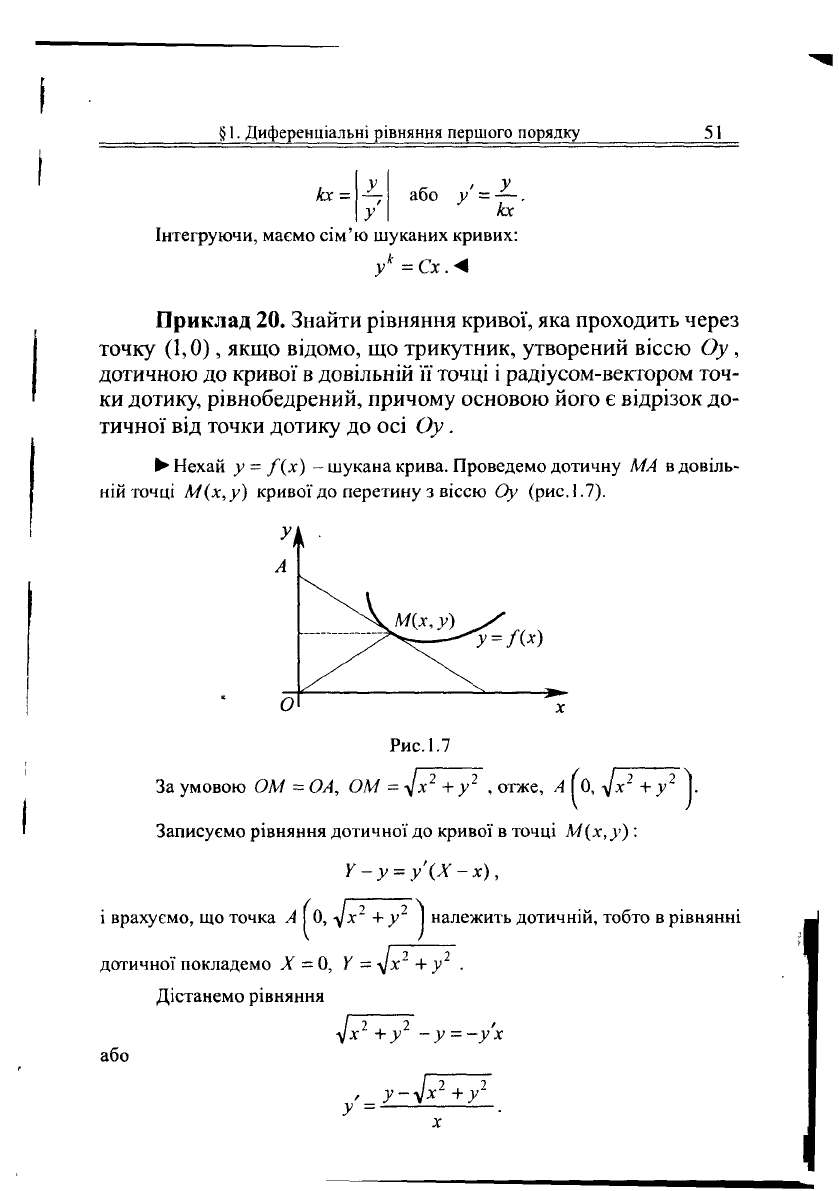
• Нехай у = /(х) - шукана крива. Проведемо дотичну МА в довіль-

ній точці М(х,у) кривої до перетину з віссю Оу (рис. 1.7).

Рис.

1.7

За умовою ОМ = ОА, ОМ = V*

+ у

, отже, А ^0, V*

+ у

Записуємо рівняння дотичної до кривої в точці М(х,у):

У-у =

у'(Х-х),

врахуємо, що точка А ^0, -^х

+ у

^ належить дотичній, тобто в рівнянні

дотичної покладемо X-0, У = ^х

+ у

Дістанемо рівняння

або

2 2 '

х +у -у = -ух

Глава 1. Диференціальні рівняння

Це рівняння, однорідне відносно зміниш. Поклавши у = их, у ~их + и,

дістанемо загальний інтеграл:

Г, 2 а"" /, ї

их + и = и-\] + и , —х = -у\ + и ,

ах

сій _ ах

л/і + И

2 Х

!п М +

л/і

+ М

:-ІпЬс +1п С

м + >/і + г/

= —, у + ^х

+ у

= С .

Використавши початкову умову у(1) = 0, знайдемо С - 1.

Отже, рівняння шуканої кривої мас вигляд

у + ^х

+у

= І.М

Приклад 21. Знайти ортогональні траєкторії сім'ї кубіч-

них парабол у = ах

• Знайдемо диференціальне рівняння даної сім'ї, виключаючи пара-

метр а із системи рівнянь

\у = ах

[у' = Зах

Отримуємо

/=—

Використовуючи означення сім'ї ортогональних траєкторій, запише-

мо їх диференціальне рівняння:

/ х

"'-Ту'

Загальний інтеграл цього рівняння

+3у

=С

є рівнянням сім'ї ортогональних траєкторій (еліпсів).^

Задачі фізики

Приклад 22. Нехай и = ху - потенціал швидкостей плос-

копаралельної течії рідини. Знайти рівняння лінії течії рідини.

Диференціальні рівняння першого порядку

• Відомо, що лінії течії є ортогональними траєкторіями сім'ї еквіпо-

тенціальних ліній (тобто ліній рівного потенціалу) ху-С. Знаходимо куто-

вий коефіцієнт дотичної до еквіпотенціальних ліній:

Це є рівняння сім'ї гіпербол.

Приклад 23. Циліндричний резервуар, у дні якого є отвір,

заповнено рідиною. Знайти час

за який рідина витече з резер-

вуару, якщо висота стовпа рідини дорівнює Н, радіус циліндра

г,

площа отвору 5 .

• Скористаємось законом Торичеллі, згідно з яким для малих отворів

швидкість витікання рідини знаходять за формулою

= -^2ф , де к - висо-

та стовпа рідини над отвором, £ - прискорення сили тяжіння.

Нехай у момент часу / висота рідини дорівнювала к і за час сії змен-

шилась на сік. Вважаючи, що протягом часу сії швидкість витікання була

сталою і дорівнювала ^2%к , знайдемо об'єм сіУ рідини, яка витекла за час

ді

(рис.

1.8):

ху + у = 0, у --.

Отже, диференціальне рівняння ліній течії рідини має вигляд:

у'-—

або уау —х сіх.

Інтегруючи, отримуємо

-у

=С.

л.

Рис.

1.8

З іншого боку, рівень рідини понизився на сік, тому

= -7іг

сік .

Глава 1. Диференціальні рівняння

Прирівнюючи елементарні об'єми, дістанемо диференціальне рівняння

звідки

Ж-

кг

сІИ

8^ Лі '

Інтегруючи, маємо

І =

2кг

З умови Н(0) - Н знаходимо сталу С = 2кг^ л//7 , тому

і =

2пг

(^Її-Ги).

Поклавши п - 0 , знайдемо час, за який витече вся рідина:

8у[2^

Приклад 24. Відомо, що нагріте до температури Т

тіло

помістили в середовище, температура якого стала і дорівнює

Г| (Г

> Г|). Знайти залежність температури тіла від часу.

• Згідно із законом Ньютона, швидкість охолодження тіла пропорційна

різниці між температурою тіла і температурою навколишнього середовища.

Нехай в момент часу / температура Т тіла дорівнює Т(і). За умовою

^ = -А(Г-Г,), к>0; Т(0) = Т

аі

(знак мінус вказує на зменшення температури).

Відокремлюючи змінні та інтегруючи, маємо

Т = Т

+Се~

Г = 7Ї +(Т

-Т

)е~

к>

Приклад 25. Експериментально встановлено, що швид-

кість радіоактивного розпаду речовини пропорційна її кількос-

ті в даний момент часу. Вказати закон зміни маси речовини від

часу, якщо при ( = 0 маса речовини дорівнювала ш

Диференціальні рівняння першого порядку

• Нехай т = т(і) - маса речовини в момент часу /. За умовою

^---кт,

к > 0; т(0) = т

()

сії

де к - коефіцієнт пропорційності. Знак мінус береться тому, що маса речо-

вини зменшується. Розв'язуючи отримане рівняння, дістаємо

т = т

є'

" . -4

Приклад 26. Знайти залежність сили струму / від часу /

в контурі, який має електрорушійну силу

Е,

опір К та індуктив-

ність Х,де

Е,

Я, Ь - сталі.

• Згідно з законом Ома, маємо

І^-+Л/ = Е.

сії

Розв'язуючи це лінійне рівняння заміною / =

ИУ

, дістанемо загаль-

ний розв'язок

--< Е

І(1) = Се '• +-,

де С - довільна стала, яку знайдемо при / = 0:

Е_

К '

Отже,

/(0) = 0, С-

(

1-е '<

IV. Задачі для практичних занять

Основні поняття

1.1. Перевірити, чи є функція у = у{х) розв'язком задано-

го диференціального рівняння:

а) у = 5х

, ху' = 2у ;

б) у -

+ 4 і§ х , у' = у сІ§ х + 2 сІ§ х ;

Глава І. Диференціальні рівняння

в) у = е

у'$тх

= у\пу;

г) у = е~

~ , у' = хе

(\ + у

1.2. Перевірити, чи є функція у = у(х,С), де С - довільна

стала, розв'язком заданого диференціального рівняння:

а)у = {Се

2х

+е

, у'

2у =

;

б) У = х (С -

1п

х |), (х - у)

сіх

+ х

(іу

= 0;

г)^

= Сх + —, ху -у

— = 0.

1.3. Показати, що функція у = у(х,С), задана неявно, є

інтегралом диференціального рівняння (С - довільна стала):

а) х

+у

=Су

, хуах = (х

-у

)сіу;

6)е

х/у

=Су, хуу'-у

=х

у;

в) х

+5ІП

х + у

-С = 0, 2у/+3х

+зіп2х - 0 ;

г) 2х

у-\ = Се

2у

,(2х + у + \)сіх-(4х + 2у-3)сіу = 0.

1.4. У заданій сім'ї кривих виділити рівняння кривої, яка

задовольняє наведену початкову умову:

а)у(\-Сх) = \, МІ) = 0,5;

б)

= 2 + Ссо5х, у(0) = -\.

1.5. Скласти диференціальне рівняння сім'ї кривих:

а) парабол у = х

+ 2ох ;

б) гіпербол у = —;

в) ланцюгових ліній у = а сЬ х;

г) гіпербол х

- у

= 2ах .

1.6. Скласти диференціальне рівняння прямих, що прохо-

дять через задану точку М(а, Ь).

§1.

Диференціальні рівняння першого порядку

1.7. Скласти диференціальне рівняння парабол, вершини

яких проходять через точку М(-1,3) і мають за вісь симетрії

пряму х - -1.

1.8. Методом ізоклін побудувати наближено сім'ю інтег-

ральних кривих заданих диференціальних рівнянь:

а) у' = х + у; б) у' =

+ у ;

в)/

= -

—;

т)у' = у-х

Диференціальні рівняння з відокремленими та

відокремлюваними змінними та звідні до них

У задачах

1.9-1.19

розв'язати задані диференціальні рів-

няння з відокремлюваними змінними.

1.9. (ху

х)ах

(у- х

у)сіу = 0 .

1.10. хуу =

- х

. 1.11. уу' = -——.

1.12.

у'\%х-у

= а. 1.13. ху'

у = у

1.14. / +

1-У

1.15.

сїх

+ уліі-х

с1у

= 0.

1.16. / = 10

1.17.

уе

2х

сіх-(\

+ е

2х

)сІу = 0.

1.18. (1 + у) (е

ііх - е

2у

сіу) -

+ у

)

сіу

= 0.

1.19. 4у-2->[у\пхсІх = Ц.

У задачах 1.20 - 1.23 заміною шуканої функції звести дані

диференціальні рівняння до рівнянь з відокремлюваними змін-

ними та розв'язати їх.

1.20. у' = соз(х + у). 1.21. у = $\п(у - х -1) .

1.22. / = (4х +

+ 1)

. 1.23. у' = Зх-2у + 5.

Глава

1. Диференціальні рівняння

У задачах 1.24 - 1.29 знайти частинні розв'язки диферен-

ціальних рівнянь, які задовольняють задані початкові умови.

1.24. _/зіпх = у\пу ; у(—

І 2 ,

е.

> 1+ у

1.25./

= -^;

Х0)

= 1.

+ х

1.26. 8ІП_УС08ХЙ?У = соз у з'тхсіх; >>(0)

1.27. у-х/ =

й(1

+ хУ); у(\) = \.

1.28. (ху

+х)ф + (х

;у-.у)</х=:0; у(1) = 1.

1.29. у 1%х = у; у

'"•=і.

Розв'язати задані геометричні та фізичні задачі, що зводяться

до диференціальних рівнянь з відокремлюваними змінними.

1.30. Знайти лінію, яка проходить через точку А^(2;3), і

таку, що відрізок будь-якої її дотичної, який міститься між ося-

ми координат, ділиться точкою дотику навпіл.

1.31. Знайти всі лінії, для яких відрізок дотичної між точ-

кою дотику і віссю абсцис ділиться пополам у точці перетину з

віссю ординат.

1.32. Знайти лінію, яка проходить через точку К(2;

і таку,

що відрізок дотичної між точкою дотику і віссю ординат має

сталу довжину І - 2 .

1.33. Знайти криві, для яких відрізок, що його відтинає

дотична на осі Ох , пропорційний квадрату абсциси точки до-

тику (к - коефіцієнт пропорційності).

1.34. Знайти рівняння кривих, у яких довжина відрізка

нормалі (відрізок її від точки кривої до осі абсцис) стала вели-

чина, яка дорівнює а.

1.35. Знайти лінію, що проходить через точку К(а,

і має

сталу піддотичну, довжина якої дорівнює а .

Диференціальні рівняння першого порядку

1.36. Знайти лінію у = /(х) (/(х) > 0, /(0) = 0), яка об-

межує криволінійну трапецію з основою

[0,

х], площа якої про-

порційна (п +1) -ому степеню /(х). Відомо, що /(1) = 1.

1.37. Знайти рівняння кривої, яка проходить через точку

1 \

1,—

, якщо для кожного відрізка [1,х] площа криволінійної

трапеції, яка обмежена відповідною дугою цієї кривої, дорів-

нює відношенню абсциси х кінцевої точки до ординати.

1.38. Матеріальна точка маси т =

г рухається прямолі-

нійно під дією сили Р , прямо пропорційної часу /, що відрахо-

вується від моменту / = 0, і обернено пропорційної швидкості

руху точки. В момент с швидкість г=0,5м/с, а сила

Р = 4

•

10~

Н. Яка буде швидкість через хвилину після початку

руху?

1.39. Моторний човен рухається в стоячій воді із швидкіс-

тю У

= 20 км/год. Через 40 с після того, як двигун виключа-

ють,

швидкість човна зменшується до V, = 8 км/год. Опір води

пропорційний швидкості руху човна. Визначити швидкість чов-

на V через 2 хвилини після зупинки двигуна.

1.40. У дні циліндричної посудини з поперечним перері-

зом 5

СМ

вертикальною віссю є малий круглий отвір площею

<у см , який закритий діафрагмою. У посудину налита рідина

до висоти

В момент і = 0 діафрагма починає відкриватися,

причому площа отвору пропорційна часу і повністю отвір від-

кривається за Т с. Якою буде висота Н рідини в посудині через

с з початку експерименту?

Диференціальні рівняння, однорідні відносно

змінних, та звідні до них

У задачах 1.41 - 1.52 розв'язати задані диференціальні рів-

няння, однорідні відносно змінних.

1.41./ = 4-2. 1.42./ = ^.

х х- у

Глава 1. Диференціальні рівняння

1.43. хау - усіх = уйу. 1.44. у =

•

^^'г

х ~ у

1.45./ = - + ^. 1.46. ху'~у =

4х

Ту

У х

1.47. ху = у1п—.

1.48. (Зу

+ 3ху + х

)ах = (х

+ 2ху)сіу.

1.49. / =

—

+ 8ІП—. 1.50. хсіу - у совіп—ах = 0.

хх х

сі ' , . У і ' X

+ХУ + У

1.51. ху = у + хі%~. 1.52. у --——.

У задачах 1.53 - 1.56 заміною шуканої функції звести за-

дані диференціальні рівняння до рівнянь, однорідних відносно

змінних або до рівнянь з відокремлюваними змінними та роз-

в'язати їх.

1.53./--*

+ 2

їх - у + 4

2х-у + \

1.54. у = .

х-2у+1

1.55. (х

у + \)ах =

(2х-г-2у-\)сіу.

(х

у-[)

У задачах 1.57 - 1.62 знайти частинні розв'язки однорід-

них диференціальних рівнянь, які задовольняють задані почат-

кові умови.

1.57. (х/-у)агсі

^ = х; у(1) = 0.

1.58.

(у

-Зх

)с1у +

2хусіх = 0; у(0) = 1.

Іеп

- 2ху~х

1.59. у <

; у(1) =

-1.

+ 2ху - х