Теоретическая механика - теория, задания и примеры решения задач

Подождите немного. Документ загружается.

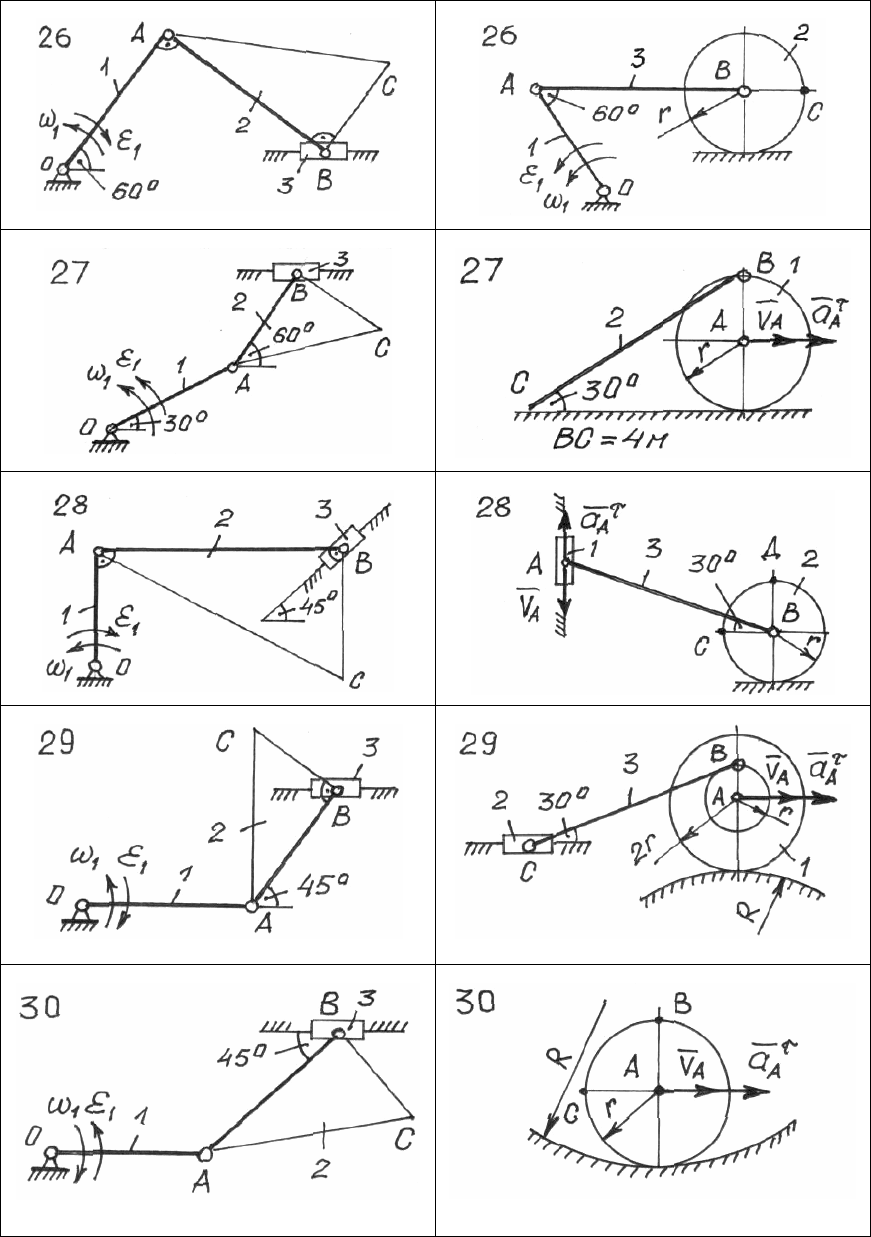
120

Рис.85

121

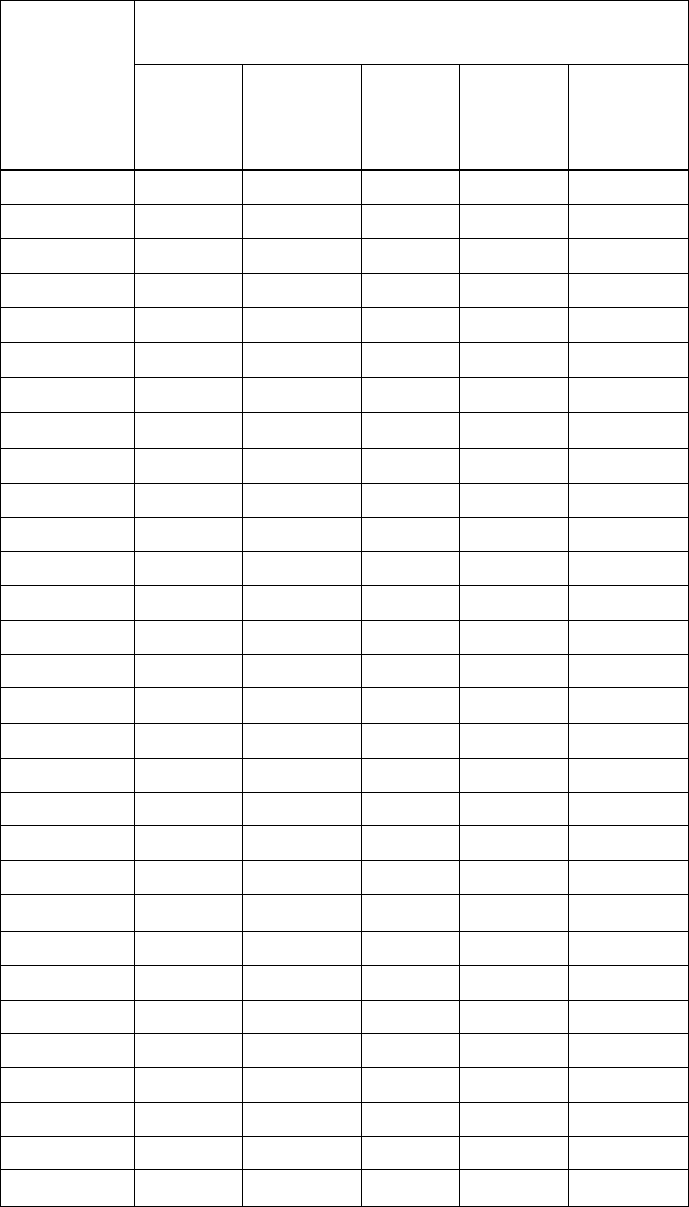
Таблица 6

З а д а ч а К 3.1

Номер

вариан-

та (рис.

80-85)

-1

-2

AB,

BC,

1 1 2 2 4 3

2 1 2 3 4 3

3 2 2 3 4 2

4 1 2 3 4 2

5 1 2 3 4 3

6 2 2 3

√

7 2 1 2 6 2

8 2 2 1,6 4 1

9 1 2 3 4 2

10 2 1 2 5 2

11 1,4 2 2 4 3

12 1,6 1,8 2 4 2

13 1,2 2 2 4 3

14 2 1,2 2 6 2

15 1,4 2 3 2 1

16 2 1,4 2 4 2

17 1,4 2 3 4 3

18 1 2 3 5 2

19 1,6 2 3 6 3

20 1,2 2 2 6 2

21 1,4 1,6 3 4 1

22 1,2 1,4 2 4 2

23 1,4 2 3 4 1

24 1,2 1,6 2 3 2

25 1,6 1,8 2 4 1

26 1,2 2 3 6 2

27 1,4 1,6 3 4 2

28 1 2 4 8 2

29 1,4 1,8 3 6 2

30 1 2 2 6 2

122

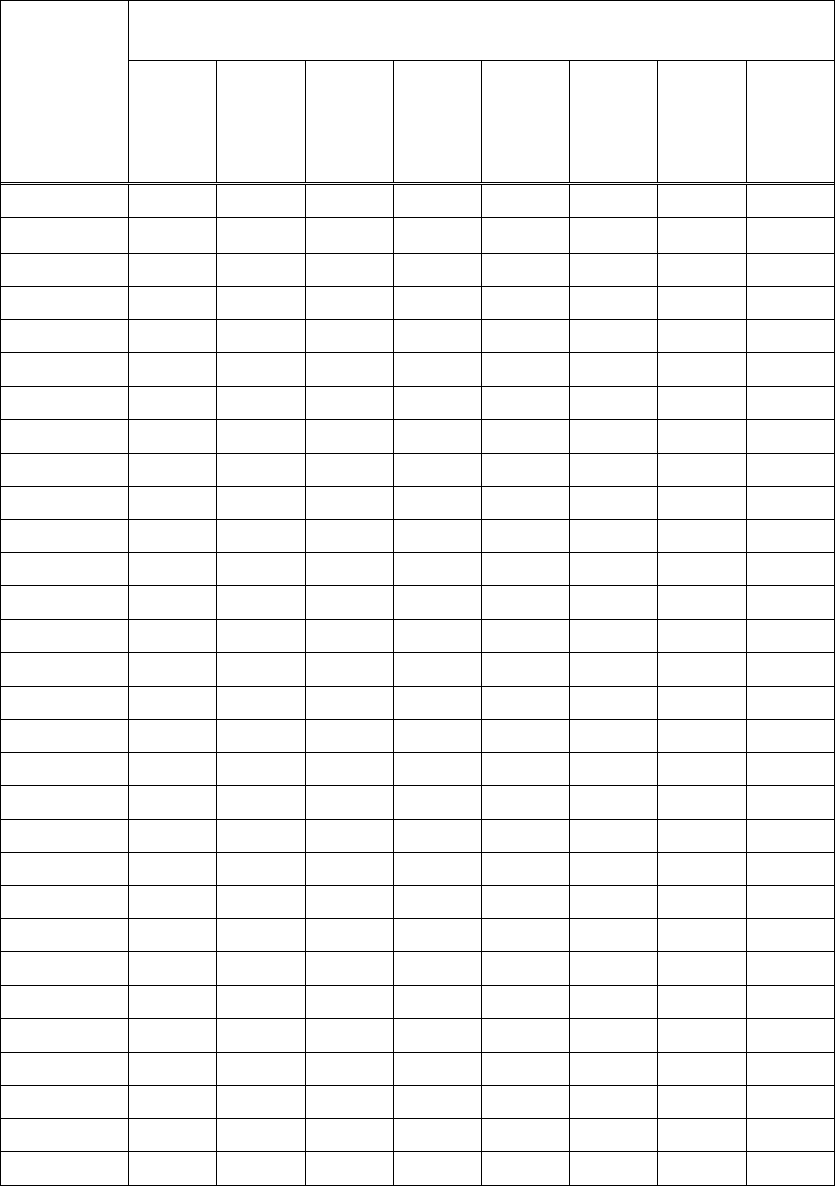
Таблица 7

З а д а ч а К 3.2

Номер

вариан-

та (рис.

80-85)

-1

-2

м/с

1 1 2 – – 1 – 0,5 –

2 2 1 – – –

√

0,5 –

3 – – 2 4 – – 0,5 2

4 2 2 – – 2 – 1,2 –

5 2 0 – – – 1 0,5 –

6 1 2 – – 2 – 0,5 –

7 – – 3 2 – – 1 3

8 – – 2 2 – – 1 –

9 – – 2 2 – – 1 –

10 – – 1,5 2 – – 0,8 –

11 1,2 1,8 – – – 3 1 –

12 2 0 – – 1,2 – 0,8 –

13 1,6 1,4 – – 3 4 0,8 –

14 1,4 1,8 – – 4 – 1,2 –

15 – – 2 1,4 – – 0,8 –

16 – – 1,4 2 – 4 0,5 2

17 – – 1,2 2 – 3 0,5 2

18 1,2 1,8 – – 2 4 0,8 –

19 – – 1,4 1,8 – 3 0,5 0,8

20 – – 1,2 2 – 4 0,4 0,8

21 2 0 – – 2 3 0,6 –

22 1,4 – – – 3 – 0,8 –

23 1,2 1,6 – – 2 4 0,6 1,2

24 1,4 2 – – – 4 0,8 2

25 – – 1 2 – 4 0,6 1,4

26 1,4 1,2 – – 2 4 0,5 –

27 – – 1,2 1,4 – – 0,8 –

28 – – 1,4 2 – 4 0,6 –

29 – – 1,6 1,4 – 6 0,5 3

30 – – 1,6 2 – – 0,4 2

123

кости П. Если отрезок АВ принадлежит фигуре (σ), то его движение

в плоскости П полностью определяет плоское движение тела 1.

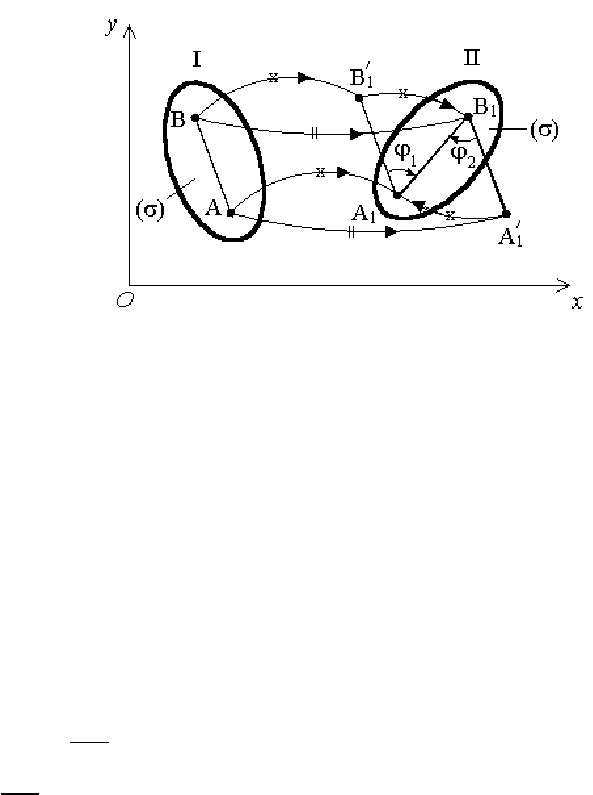
Рассмотрим перемещение отрезка АВ в своей плоскости из одно-

го положения в другое (рис. 86). Перемещение фигуры (σ), с отрез-

ком АВ, из одного положения (I) в другое (II) можно разложить на

поступательное движение

вместе с полюсом (т. А) и вращение

фигуры (σ) (или АВ) в плоскости xOy вокруг полюса (т. А) на угол ϕ

до совмещения с новым положением отрезка А

Рис. 86

За полюс можно выбрать другую точку (т. В), тогда вращение бу-

дет вокруг точки В

на угол ϕ

. Но



(ω

= ω

Важно отметить, что поступательное движение фигуры (

σ) (от-

резка АВ) зависит от выбора полюса, а вращение не зависит от вы-

бора полюса.

2. Скорости точек тела при плоском движении

В дальнейшем будем рассматривать плоское движение отрезка

АВ (или вектора

) в плоскости чертежа рисунка.

Вектор

(рис. 87) будет поступательно перемещаться с полю-

сом (т. А) и вращаться вокруг полюса. Тогда уравнения движения

плоской фигуры (

σ) можно записать в следующем виде:

= x

(t); y

= y

(t);

(t).

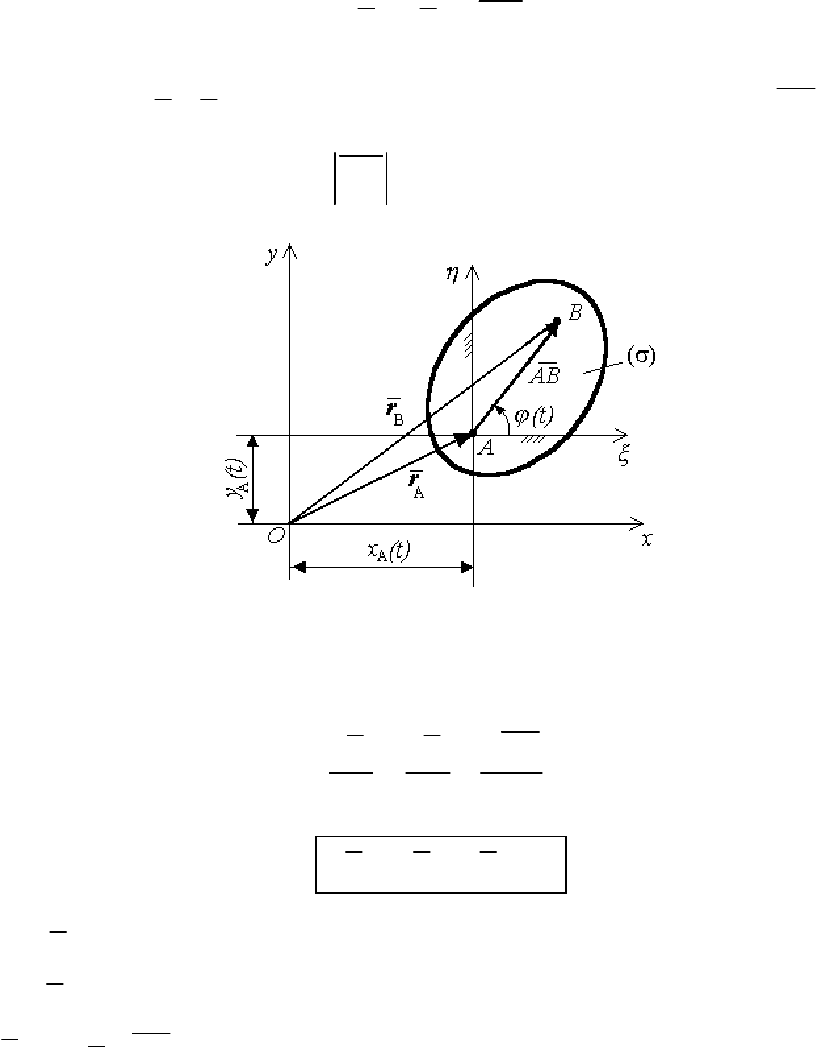
124

Оси координат xOy неподвижны, а оси координат ξAη непосредст-

венно связаны с фигурой (

σ). Из векторного треугольника ОАВ вид-

но, что

rrAB=+ , (1)

где векторы

r ,

r меняют модуль и направление, а вектор AB ме-

няет только направление ( AB = const).

Рис. 87

Продифференцируем по времени равенство (1)

dr dr

dAB

dt dt

получаем , (2)

где

v - вектор скорости точки B,

v - вектор скорости точки A,

/BA

VAB

=× - скорость точки В во вращательном движении фигу-

ры (

σ) вокруг полюса точки A (формула Эйлера).

Таким образом, скорость любой точки фигуры при ее плоском

движении равна векторной сумме скорости полюса и скорости этой

BABA

vvv

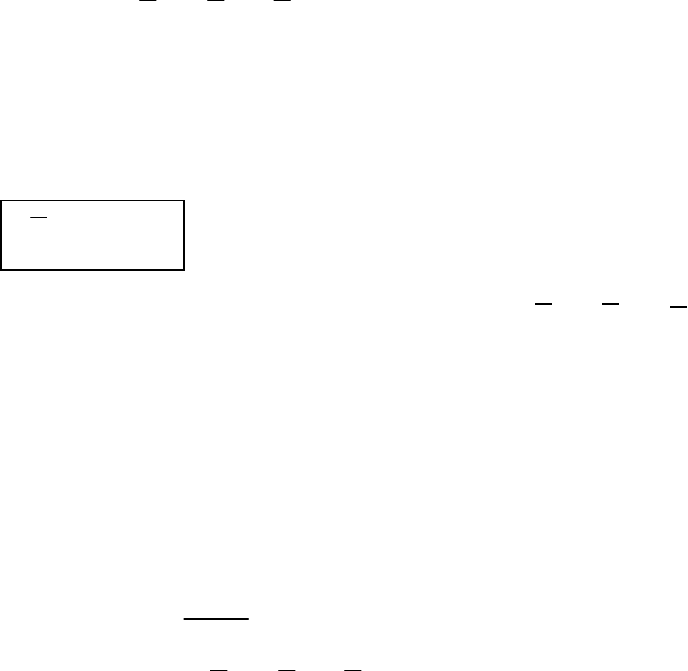
125

точки при вращении фигуры вокруг полюса.

При кинематическом расчете механизма за полюс выби-

рается точка, скорость которой всегда будем знать по мо-

дулю и направлению.

Векторное равенство (2) является одним из способов определе-

ния скорости точки фигуры при ее плоском движении.

3. Решение векторного уравнения

При решении векторного уравнения (2) в первую очередь необ-

ходимо сделать анализ каждого вектора, входящего в него. Приме-

няем правило знаков: «+» – знаем; «–» – не знаем. Для решения

уравнения (2) необходимо иметь максимум только два минуса.

a) Пусть

BABA

vvv=+ , (3)

– + + + – +

где первый знак под вектором – модуль, а второй – направление.

Минусы в левой и правой частях равенства. При этом всегда

/BA

V AB⊥

, а по модулю V

B/A

⋅

AB. (4)

В точке B будет сосредоточено три вектора:

v ,

/BA

v . Через

точку

B проводим прямоугольную систему координат xBy и на эти

оси проецируем равенство (3):

cos sin

sin cos

BAxBA

BAyBA

vvv

Решая систему двух уравнений, находим V

и V

B/A

. Решая формулу

(4), находим

= .

б) Дано

BABA

vvv=+ , (5)

– – + + + +

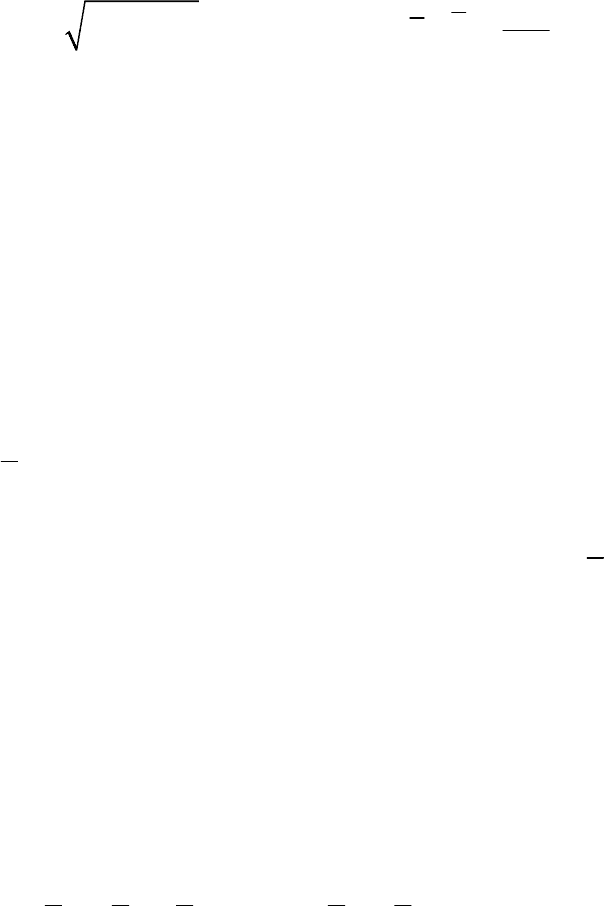
126

где минусы только в левой части равенства. Так же выбираем оси

координат

XBY и равенство (5) проецируем на эти оси:

= v

+ v

B/A

;

= v

+ v

B/A

Из уравнений нашли проекции скорости точки B, тогда

Bx By

=vvv, ()

cos v ; i =

∧

В этом случае должны знать

, так как

BA AB

vAB

⋅ .

4. Мгновенный центр скоростей

При плоском движении фигуры (σ) в каждый момент времени,

при

ω ≠ 0, существует такая точка, скорость которой равна нулю.

Эта точка называется мгновенным центром скоростей (МЦС). Рас-

смотрим схему рис. 88. Точку

А фигуры (σ) выбираем за полюс, так

как скорость

v этой точки известна по модулю и направлению, а

также знаем угловую скорость

ω вращения фигуры относительно

полюса. Проведем луч AN, перпендикулярный скорости

v , и стро-

им эпюру скоростей точек этого луча при поступательном движении

фигуры, которая будет иметь форму прямоугольника. Треугольник –

эпюра скоростей тех же точек при вращательном движении фигуры

(

σ) вокруг полюса т. А. При этом замечаем, что в точке P имеем два

вектора скорости, лежащие на одной прямой, противоположно на-

правленные и равные по модулю. Следовательно, скорость этой

точки равна нулю (

= 0).

PAPA

vvv=+ или

APA

= .

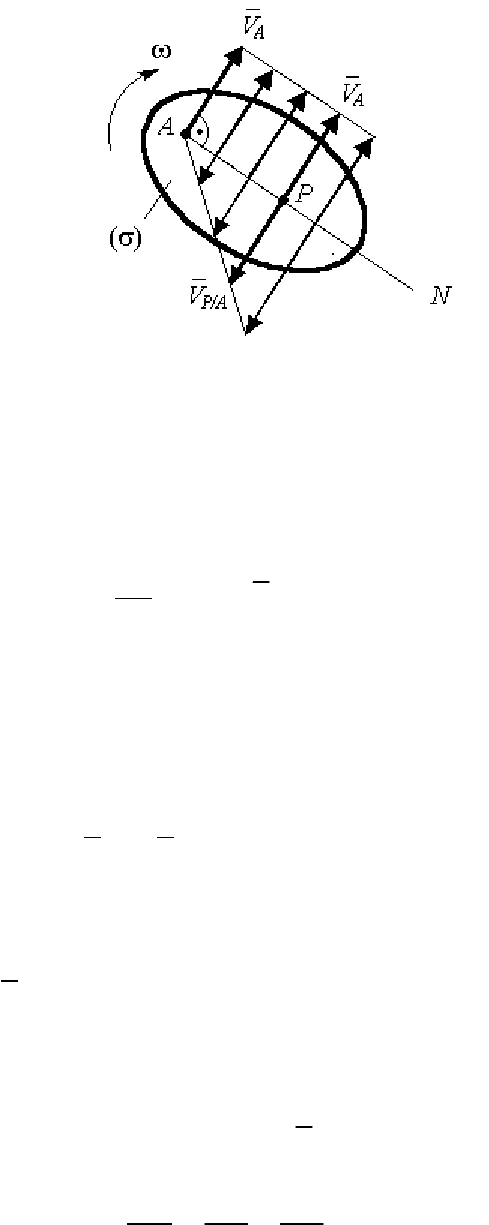
127

Рис. 88

По модулю

/APA

VV= , но

VAP

=⋅ . Тогда расстояние от по-

люса

A до МЦС точки P определится по формуле

, где

V ⊥ AP.

5. Определение скоростей точек плоской фигуры

при помощи МЦС

Для нахождения МЦС фигуры нужно в точках приложения ско-

ростей двух точек

V и

V восстановить перпендикуляры к направ-

лениям скоростей, которые пересекутся в точке

P. Это будет МЦС

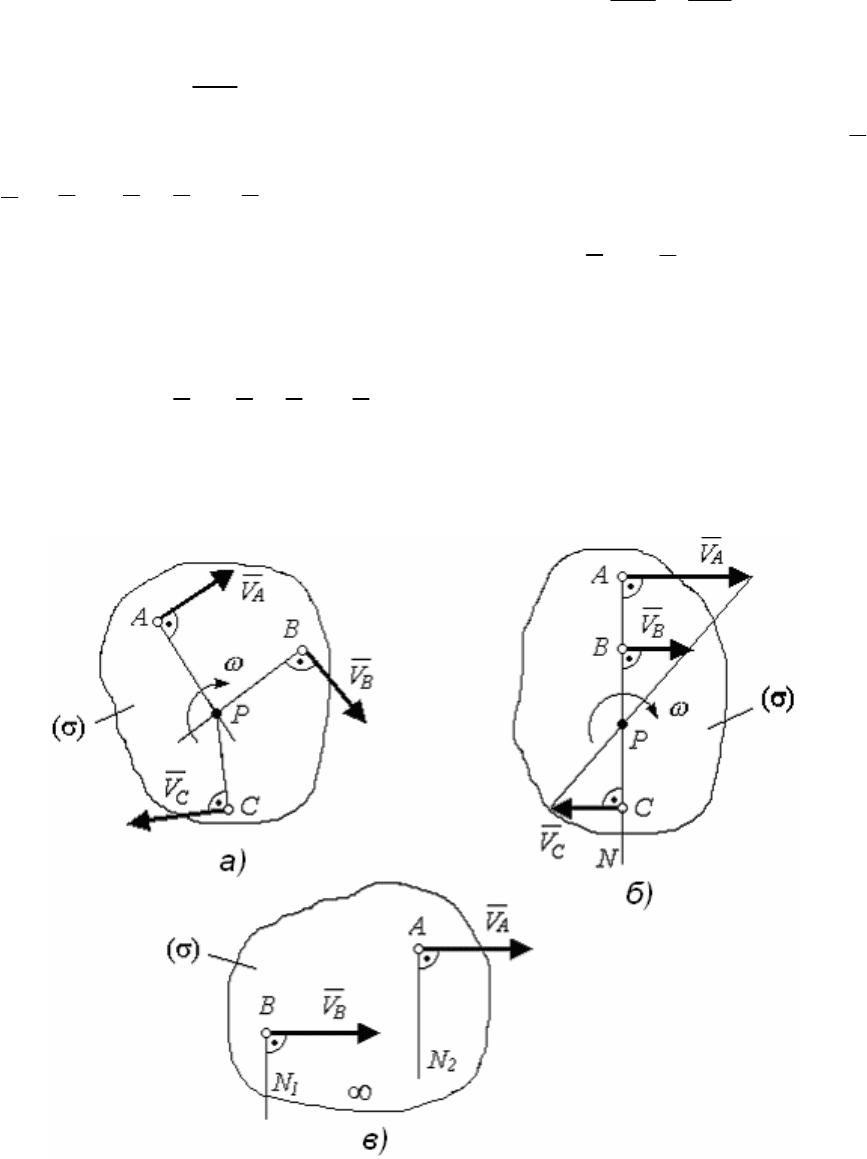
(рис.89а).

Скорость

стремится вращать фигуру по ходу часовой стрелки,

поэтому в ту же сторону показываем

ω. Для определения направле-

ния скорости точки C нужно эту точку соединить с МЦС и в сторону,

как показывает

ω, провести вектор

V перпендикулярный РС.

Угловая скорость

ABC

AP BP CP

vvv

====

… . Для определения ско-

128

рости точки B нужно использовать пропорцию

AP BP

= . Зная v

находим

vv= .

В другом случае (рис. 89

б), когда точки приложения скоростей

v (

;

) лежат на одном перпендикуляре AN, для оп-

ределения МЦС нужно через концы векторов

v и

провести пря-

мую, которая пересечет перпендикуляр

AN в точке Р (МЦС).

Если перпендикуляры

и AN

пересекаются в бесконечности

(

|| AN

), то

, в данный момент времени ω = 0,

фигура будет перемещаться мгновенно – поступательно (рис. 89

в).

Рис. 89

129

Следует помнить, что при определенном положении плос-

кого механизма, каждое звено имеет свой мгновенный центр

скоростей.

6. Ускорение точек тела при плоском движении

Равенство (2) запишем в виде

ABvv

=+× и продифферен-

цируем его по времени:

ddd dAB

dt dt dt dt

=+×+×.

Тогда

= a - вектор ускорения точки В;

= a

- вектор ускорения полюса (точки А);

AB AB

×=×=a - касательное ускорение точки B во

вращательном движении фигуры относительно полюса; вектор

всегда перпендикулярен

АВ; по модулю

⋅a

;

BA B/A

dAB

ωω

×=×=a - нормальное ускорение точки В, кото-

рое всегда направлено к полюсу (точка А); по модулю

=⋅a

Для точки

В окончательно можно записать

. (6)

Это векторное уравнение решается так же, как уравнение (2).

Вектор ускорения точки

B состоит из геометрической суммы трех

векторов:

;

/BA

a ;

a (рис. 90).

aaaa

++=