Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

702

−+ + =

0xkx xxω   ,

(24.3.10)

which has a fixed point at the origin; there appears a Hopf bifurcation when

passes

from negative to positive values. Some phase portraits for various values of

k are given

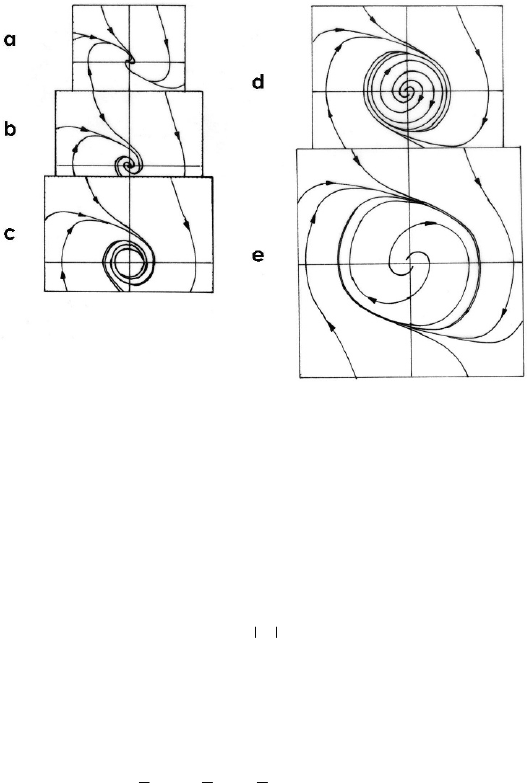
in Fig. 24.35. If

<−2k , then the origin is an asymptotically stable node (Fig. 24.35a),

obtaining a stable spiral for

=−2k (Fig. 24.35b). For = 0k (Fig. 24.35c) we obtain

the bifurcation, the convergence being very weak, while for

> 0k we get an instable

spiral, the flux tending to the limit circle to which it gives rise (Fig. 24.35d). If

> 2k

then the origin is an instable node and the limit circle continues to increase

(Fig. 24.35e). Changing the sense of the flux, we pass from a phase portrait of a Hopf

supercritical bifurcation to a phase portrait of a Hopf subcritical bifurcation.

Fig. 24.35 Phase portraits for the non-linear differential equation (24.3.10): 2k <− ,

asymptotically stable node (a); 2k =− , stable spiral (b); 0k = , bifurcation (c);

0k >

, instable spiral (d);

2k >

, instable node (e)

In connection with the Hopf bifurcation can be put the Neimark bifurcation (second

bifurcation of Hopf), which describes the continuous increase of a second mode of

oscillation, starting from a limit circle.

The possibility of appearance or of disappearance of a periodic solution of the

differential equation

( , ), , , 0

Dccλα=∈⊂<>



xfx x

(24.3.11)

where

f is an analytic real function definite on ×−[,]Dcc, is put in evidence by

Theorem 24.3.1 (Hopf). Let be an analytic real vector function

, so that

((), )λλ= 0fg ; we express fx(, )λ in the form

(, ) (, ), ()

λλλ

∗

=+ =−fx Lx f x x x g ,

(24.3.12)

Dynamical Systems. Catastrophes and Chaos

703

where

is an n -dimensional square real matrix, which depends only on λ , while

∗

fx(,)λ is the non-linear part of fx(, )λ . We assume that there exist only two

complex conjugate eigenvalues

(), ()αλ αλ of

with the properties =Re (0) 0α

and

≠Re[d (0)/ d ] 0αα. In this case, the system of differential equations (24.3.11)

has a periodic solution

x(, )t ε of period ()T ε with = ()λλε, so that

(0) , ( ,0) (0)tλλ==xg and ≠xg(, ) ( ( ))t ελεfor any parameter ≠ 0ε sufficiently

small; moreover,

()λε , x(, )t ε and ()T ε are analytical in = 0ε , while

=(0) 2 / | Im (0) |T πα. These “small” periodic solutions exist only for one of the

three cases: for

< 0λ or for > 0λ or for = 0λ .

We mention that the theorem does not specify how “small” must be

ε .

The Hopf bifurcation allows – as well – the generation of periodic solutions. Thus, if

a position of equilibrium is stable for

λλ

and become instable for

λλ

, then can

appear a stable position of equilibrium; the orbit is developed starting from a point in

the phase plane (for

λλ

) to closed curves, by continuous deformations, as λ is

greater than

λλ

. This is the soft generation.

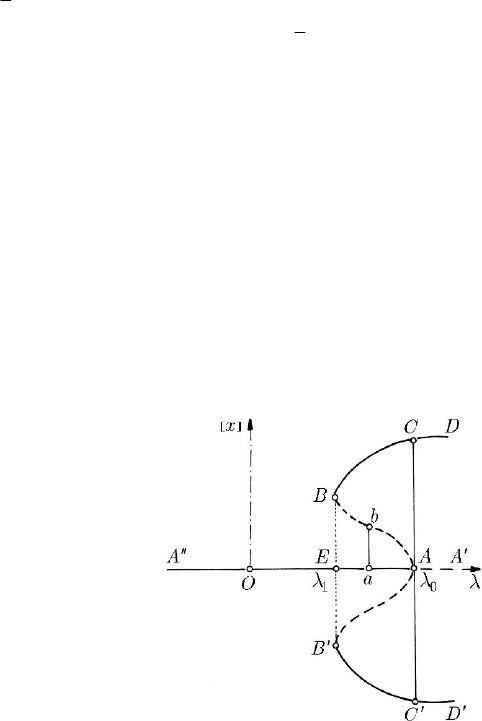
Fig. 24.36 Hard generation of a periodic motion

If the generation of the periodic motion takes place by a jump, in the sense that the

amplitudes of the periodic motion have – from the very beginning – relative great finite

values (not increasing continuously from zero to a finite value, as far as

λ is increasing),

then we have to do with a hard generation. In Fig. 24.36 is represented the variation of a

variable

x[], definite in Sect. 24.2.1.1, as function of λ ; one can see that there are possible

periodic motions for

λλ

too. On the semi-straight line

′′

, for which

λλ

, the

solution

=x[] 0 is stable, while on the semi-straight line

′

, for which

λλ

, this one

is instable. One observes that for

λλ

a stable periodic motion is possible (the curve

BCD

or the curve

′′′

BCD

), as well as an instable periodic motion (the curve BA or the

curve

′′

). We see – as well – that for λ somewhat smaller than

, the system being in

a stable equilibrium, a periodic motion with a sufficiently great amplitude can be suddenly

MECHANICAL SYSTEMS, CLASSICAL MODELS

704

generated (the segments of a line

AC or AC

′

). It is possible that, for >

λλ, for

sufficiently great perturbations, the position of stable equilibrium does disappear, a periodic

motion of a sufficient great amplitude taking place, especially if

λ approaches

λ , even if

λλ. If λ corresponds to a point a , for a perturbation less than ab , then the system

returns to the position of equilibrium, while if the perturbation is greater than

ab , then the

system becomes – by a jump – a stable periodic motion and does no more return to the

position of equilibrium; hence, the curve

′

BAB

, which – practically – is never realized,

represents the limit between the domain of attraction of the stable position of equilibrium

EA and the domain of attraction of the periodic motion BCD (or

′′′

BCD

24.3.1.3 Lindstedt’s Method

Lindstedt has elaborated a numerical method to determine the periodic solutions of a

non-linear differential equation, using – in fact – the perturbations method, but

eliminating, at each stage of calculation, the secular terms which appear.

Let be thus the differential equation

(,)xxfxxωε 

(24.3.13)

where

ε is a small parameter and (, )fxx is a non-linear function of x and x . In the

linear case (

= 0ε ) the period of the motion is = 2/T πω; in the non-linear case

(

≠ 0ε ) we have, obviously, =+2/ ()T πω εO , hence the pulsation Ω of the

motion is of the form

=+ + +

...Ωω εω εω ,

(24.3.14)

with

= 2/TΩπ as unknown. It is convenient to make a change of independent

variable

= tτΩ, (24.3.15)

which – by replacing

t and 2/πΩ – leads to = 2τπ, hence to a known period.

Calculating

′′′

====

dd dd

xxx x

ττ

ΩΩ

ττ





where we have denoted by

′

and

′′

the derivatives of the function x with respect to

the variable

τ , we may write the differential equation (24.3.13) in the form

′′ ′

(, )xxfxxΩωεΩ

(24.3.13')

Assuming an expression

=+ + +

...xx x xεε ,

(24.3.16)

Dynamical Systems. Catastrophes and Chaos

705

where

( ), 0,1,2,...

xx iτ==, we can write

()()()

222

00 0

12 1 2 12

( , ) ..., ... ... ;fx x f x x x x x xΩεεωεωεωεε

′′′′

= +++ +++ +++

introducing in (24.3.13') and taking into account (24.3.14), (24.3.16), one obtains

()

22 22

00 0 0 0 0

111 1

22 2

000

222112

32 2

000

33312123

,, ,,

, , , , , , ... 0;

xx xxfx

xxfxx

xxfxxx

ωωεωω ωω

εω ω ωωω

εω ω ωωωω

′′ ′′

++ +−

⎡⎤

⎣⎦

′′

++−

⎡⎤

⎣⎦

′′

++− +=

⎡⎤

⎣⎦

equating to zero the coefficients of various powers of the small parameter, it results the

system

()

′′

00 0

000

111 1

000

222112

000

33312123

,, ,

,, ,, ,

,,, , , , ,

......................................................................

xxfx

xxfxx

xxfxxx

ωω

ωω ωω

ωω ωωω

ωω ωωωω

(24.3.17)

determining thus the functions

(), (), (),...xxxτττ, as well as the pulsations

,,,...ωωω Integrating the first equation (24.3.17), one obtains a periodic solution of

period

2π ; imposing now the initial condition

(0) (0)xxx== as well as the

condition

000

(0) (1/ ) /xxvΩΩ

′

== , there result

()x τ and

ω . Replacing in the

second equation we obtain – by integration –

()x τ and

ω , with homogeneous initial

conditions

(0)0, (0)0xx

′

== (because the non-zero initial conditions have been

previously verified); in the expression of

()x τ appears a secular term, the coefficient of

which is equated to zero. The procedure is repeated till the (

+ 1n )th equation, resulting

=+ ++

() ( ) ( ) ... ( )

xt x t x t x tΩεΩ εΩ,

(24.3.18)

where

=+ + ++

...

Ωω εω εω εω.

(24.3.18')

For instance, if use Lindstedt’s method for the differential equation

++ =

0xx xε ,

(24.3.19)

we get (

= 3n )

()

352

352 52

123

() cos

32 1024

13 1

cos 3 cos 5 ,

32 128 1024

xtaaat

aa ta t

εεΩ

εεΩ εΩ

=− +

++ +

(24.3.19')

MECHANICAL SYSTEMS, CLASSICAL MODELS

706

where

=+ − = =

242

321

1 , (0) , (0) 0

8256

aaxaxΩεε

 .

(24.3.19'')

24.3.1.4 Stability of Periodic Solutions

Let be the system of non-linear differential equations

=∈xxx(;),





(24.3.20)

and let

()tΦ be a solution, in general non-periodical, of this system; if y is a small

perturbation, let us take

=+xy()tΦ ,

(24.3.21)

replacing then in (24.3.20). We get

()()

()

(;)

() () ; (); ...

ttttt

⎡⎤

+= + = + +

⎢⎥

⎣⎦



yf y f y

ΦΦ Φ ,

wherefrom, taking into account that

()tΦ is a solution of the system (24.3.20), it

results (we neglect the terms in higher powers of

y )

⎡⎤

⎢⎥

⎣⎦

yyAy

()

(;)

()



(24.3.20')

hence the linearized system of the initial one; formally, we can write

∫

()

() e

ττ

(24.3.22)

If, for

→∞t , the exponential in (24.3.22) tends to infinite, then the solution

=x ()tΦ is instable, while, if this exponential tends to zero, then the solution is

asymptotically stable; a special study must be make in other cases.

In the case in which the system (24.3.20) is autonomous and the solutions are

periodical, the matrix A()t is periodical too and one can use Floquet’s theory (see

Sect. 24.1.1.3). In this order of ideas, one can state:

Theorem 24.3.2. Let be the linear system (24.3.20') with a periodic matrix A()t , of

period

T . The sum of the characteristic exponents is given by

+++ =

∫

... tr ( )d

λλ λ ττ

(24.3.23)

where

Atr is the trace of the matrix A .

Dynamical Systems. Catastrophes and Chaos

707

Theorem 24.3.3. Let be the autonomous non-linear system (24.3.1) which admits a

periodic solution

()tΦ , of period T , and for which the vector fx() is of class

C in a

domain

⊂

D  , which contains the periodic solution too. The linearized system

⎡⎤

⎢⎥

⎣⎦

()



(24.3.24)

has one null characteristic exponent; if the other

− 1n characteristic exponents have a

negative real part, then the solution

()tΦ is stable.

The stability considered above is an orbital stability, in the Poincaré sense (a

solution

x()t , which starts from a neighbourhood of the system ()tΦ remains during

the motion in the same neighbourhood).

24.3.2 Global Bifurcations

The global bifurcations are these qualitative changes which take place in the

structure of orbits in an extended domain of the phase space, by a variation of the

parameters which intervene in the system of differential equations. After some general

considerations, one presents the problem of heteroclinic and homoclinic trajectories,

giving also some examples.

24.3.2.1 General Considerations

We call phase current the operator

Φ which, applied to the vector of state

=∈xx

(0)

 , allows to obtain the solution x()t of the system of non-autonomous

equations (24.3.20) by the relation

=xx

()

t Φ .

(24.3.25)

If the system of differential equations is autonomous (we consider only such systems

in what follows), then the phase current verifies the property of translation

ΦΦΦ.

(24.3.26)

For the point specified by the vector

=∈x

[,,..., ]

xx x  , solution of the

system of autonomous equations (24.3.1), we introduce the

ω -limit point, defined by

lim ( ) ( )

t →∞

=xxΦω,

(24.3.27)

and the α -limit point, defined by

lim () ()

t →−∞

=Φαxx

(24.3.27')

In the case of the system of recurrence equations (24.1.77'), we – analogously – obtain

MECHANICAL SYSTEMS, CLASSICAL MODELS

708

−

→∞

=xx

lim ( ) ( )

f ω

(24.3.28)

−

→−∞

=xx

lim ( ) ( )

f α

(24.3.28')

tending to infinite by integers.

Fig. 24.37 Phase plane: critical point O, stable limit cycle

and instable limit cycle

As an example, let be in the phase plane (for the sake of simplicity we are situated in

 ) the critical point O , the stable limit cycle

C and the instable limit cycle

C . We

denote by

D the domain interior to the limit cycle

C and by

D the domain

contained between the two cycles (Fig. 24.37). One can notice that for all the points

situated in the domain

\DO, the point O is an

-limit point, while the limit cycle

C is an

-limit set, while the limit cycle

C is an

-limit set (as well as for the

points external to

C ).

∈→ ∈∀∈ ⊂xx() , ,

UUU

τ Φ ,

(24.3.29)

then

U is an invariant set for the phase current

Φ . In case of the system of recurrence

equations (24.2.97'), the relation of definition is

−

∈→ ∈∀∈xx

(),

Uf Un .

(24.3.29')

Referring to the preceding example, the critical point

O and the limit cycles

C and

C are invariant sets.

An ω -limit point is “non-wandering” for the phase current

Φ if, for any

neighbourhood

U of it, there exists an arbitrary great moment t , so that

∩≠()

UU0Φ .

(24.3.30)

An analogous definition can be given for the recurrence equations (24.1.77').

The fixed points and the points which form the limit cycles are, obviously,

non-wandering. We mention that not all the invariant sets are formed by non-wandering

Dynamical Systems. Catastrophes and Chaos

709

points. In general, the wandering points correspond to a transitory behaviour; a

behaviour “on long term” (asymptotical) corresponds to the orbits of non-wandering

points.

A simply connected closed set

⊂

D  , for which

() , 0

DDt⊂∀>Φ ,

(24.3.31)

is called trap-region; the mentioned condition is verified if the vector

fx() is directed

towards the interior of the domain

D at any point of its frontier. One can give an

analogous definition for the recurrence equations (24.1.77').

The set

≥

()

∩

Φ ,

(24.3.32)

where D is a trap-region, is called attraction set; hence, a set ⊂A

 is an attraction

set if there exists a neighbourhood

U of A so that ∈x()

UΦ for ≥ 0t and

→xA()

Φ for , tU→∞∀∈x .

The union of all the points which, indifferently of the moment in the past (

≤ 0t )

reach the neighbourhood

U of the attraction set A at the moment = 0t

≤0

()

∪

(24.3.33)

is called domain of attraction of the attraction set

A . The domains of attraction of the

attraction sets do not intersect, being separated by stable variations of the non-attraction

sets. Such a domain is called basin of attraction.

If an attraction set has the property of invariance

=∀∈AA() ,

t Φ ,

(24.3.34)

too, then this one is an attractor. For instance, a stable focus or a stable node are

attractors.

The structure of an attraction set can be, sometimes, very complicated. Let be thus a

one-dimensional phase current, defined by D. Ruelle’s differential equation

+=∈

sin 0,xx x



(24.3.35)

which has an infinite but numerable set of fixed points

0, 1/ , xx nn==± ∈ , the

interval

−[1,1] being an attraction set. Calculating

d()

4sin cos

xxx

ππ

=− + ,

we see that =

d(1/ )/d ( / )cosfnx n nππ; hence, the derivative is positive for an

even

n , the set of fixed points being a set of repeller (instable equilibrium), while for

MECHANICAL SYSTEMS, CLASSICAL MODELS

710

n odd the derivative is negative, the fixed points forming an attraction set (stable

equilibrium). For the fixed point

= 0x one can nothing state. Couley proposed, in

1978, that this attractor be called quasi-attractor.

24.3.2.2 Heteroclinic and Homoclinic Trajectories

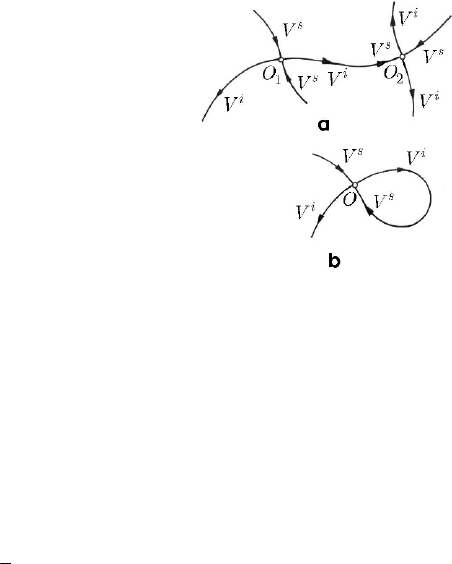
A trajectory which unites two distinct critical points

O and

O in the phase space is

called heteroclinic trajectory; we assume that

O and

O are hyperbolic critical points

and denote by

V and

V their stable and instable variants, respectively (Fig. 24.38a).

For the critical point

, the heteroclinic line is a part of its instable invariant variety,

being an ω -limit point (for →∞t ); these two points do not belong to the

heteroclinic line (being critical points, they cannot belong to other trajectories in the

phase space).

Fig. 24.38 Heteroclinic (a) and homoclinic (b) trajectories

A trajectory in the phase space which unites a critical point

with itself is called

homoclinic trajectory (Fig. 24.38b); for this point, supposed to be hyperbolic, which is

– at the same time –

ω -limit point and α -limit point and which does not belong to the

homoclinic line, the respective trajectory belongs both to the stable and to the instable

invariant variety.

The heteroclinic and homoclinic lines are both global bifurcations.

It has been shown in Sect. 24.1.1.1 that Helmholtz’s oscillator leads to a homoclinic

orbit of equation (24.2.11'') for

= 0C .

We considered in Sect. 7.2.3.4 the equation of the mathematical pendulum in a

non-linear case, which led us to the phase portrait in Fig. 7.22. The orbits corresponding

= 1h pass through the points ( ±0, 2ω ) and unite the points ( ± ,0π ); these latter

points are hyperbolic critical points, so that the corresponding orbits seem to be

heteroclinic orbits. Taking in view the periodic character of the motion, we can consider

as phase space a cylinder the points ( −

,0π ) and ( ,0π ) being coincident; hence, the

orbit (unique) is – in fact – homoclinic.

Let us consider the motion of a heavy rigid solid, fixed at its mass centre (the

Euler–Poinsot case of integrability, see Sect. 15.1.2). If we denote

111

Iξω,

222333

,IIξωξω, where

123

,,III are the central principal moments of inertia, while

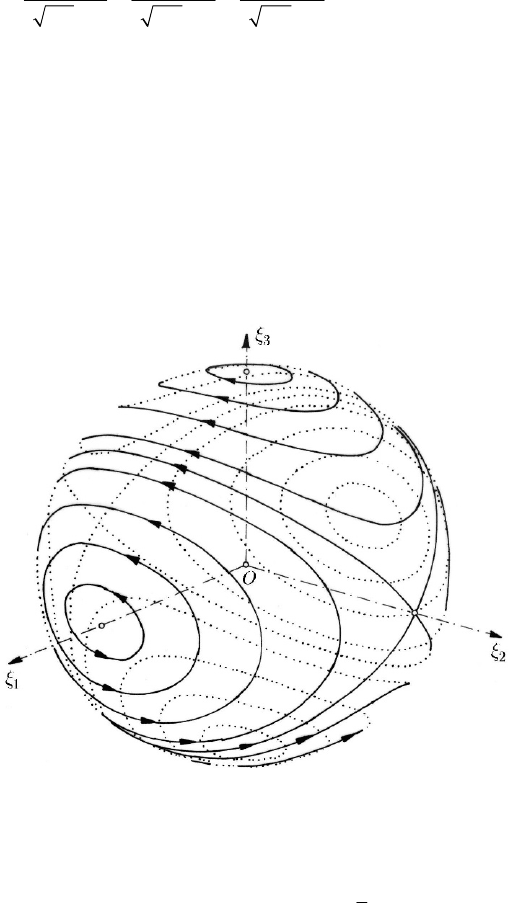
Dynamical Systems. Catastrophes and Chaos

711

123

,,ωωω are the components of the rotation velocity vector ω with respect to the central

principal axes of inertia, then we can write the first integrals (15.1.47) in the form

++=

222 2

123

222

123

222

123

(),

()()()

II II II

ξξξ Ω

ξξξ

ΩΩΩ

(24.3.36)

where

I and Ω are constant quantities of the nature of a moment of inertia and of a

rotation velocity, respectively. It result thus a sphere and an ellipsoid at the intersection

of which one obtains the searches orbits. Assuming that

≥≥

123

III, one obtains the

centres

±(,0,0)IΩ , ±(0,0, )IΩ , corresponding to the intersection of the sphere with

the stable central principal axes of inertia, and the saddle points

±(0, ,0)IΩ ,

corresponding to the intersections of the sphere with the instable central principal axis

of inertia (Fig. 24.39). One of the saddle points is an ω -limit point and the other one is

-limit point. The centres are surrounded by closed curves, while the saddle points

are united by heteroclinic trajectories.

Fig. 24.39 Representation of the motion of a heavy rigid solid fixed at its mass centre:

intersection of a sphere with an ellipsoid

The heteroclinic and homoclinic trajectories are – in general – separating domains in

the phase space with different qualitative motions; e.g., in the case of the mathematical

pendulum previously considered, the homoclinic line

= 1h separates the domain in

which the motions are periodical from the domain in which these ones are rotational.