Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

672

−=yy() () ()tt ε O ,

(24.1.85)

at the time scale

1/ε .

Let us apply the averaging method to Mathieu’s equation

++ = ∈(1 2 cos2 ) 0,xtxxε  ,

(24.1.86)

with the initial conditions

(0) , (0) 0xxx== . This equation of second order is

equivalent to the system of equations of first order

==−+

122 1

,(12cos2)xxx txε .

(24.1.86')

The solution of the linear system

122 1

,xxx x==− with the initial conditions

1122

(0) , (0)xxxx== is

=+ =−+

00 00

11 2 2 1 2

cos sin , sin cosxx tx tx x tx t;

hence, we can make the change of variable

=+ =−+

11 2 2 1 2

cos sin , sin cosxy ty tx y ty t,

(24.1.87)

being led to the system of equations

+=−+=− +

12 12 12

cos sin 0, sin cos 2 cos2 ( cos sin ),ytyt ytyt tytytε 

wherefrom

=− +

112

212

2sincos2

(

cos sin

)

2coscos2

(

cos sin

)

yttytyt



(24.1.87')

Averaging on the interval

[0,2 ]π , we obtain the system of linear differential equations

=− =−

1221

yyyyεε





;

taking into account the Theorem 24.1.11, we can write also the system

=− =−

1221

yyyyεε

(24.1.88)

of solutions

(

)

=+ =− +

cosh sinh , sinh cosh

22 22

yA tB ty A tB t

εε εε

(24.1.88')

Dynamical Systems. Catastrophes and Chaos

673

Returning to the initial variables and taking into account the initial conditions, we

obtain

(

)

=−

( ) cosh cos sinh sin

xt x t t t t

εε

(24.1.89)

which represents a very good approximation of the solution of Mathieu’s equation at

the time scale

1/ε .

We shall consider also a non-linear differential equation for which the non-autonomy

appears due to a perturbing force, function on time, e.g., the equation

(,) cosxfxx F tω  ,

(24.1.90)

equivalent to the system

==− =

,(,)cosxyy fxy F tω ;

(24.1.90')

the change of variable

=− =−() ()cos ()sin , () ()sin ()cosxt ut t vt tyt ut t vt tωω ωω

(24.1.91)

corresponds to a clockwise rotation, of angular velocity

ω , in the plane Oxy , which

leads to the plane

Ouv

, called the Van der Pol plane. The system (24.1.90') becomes

==(,, ), (,, )u uvtv uvtϕω ψω



(24.1.91')

We assume that, by the motion of rotation, the functions

()ut and ()vt do not vary

much during a period

= 2/T πω, so that we can apply the averaging method; we get

∫∫

(,, )d, (,, )d

uuvttvuvtt

ϕω ψω





(24.1.91'')

In the frame of the hypothesis made, we take

≡≡,uuvv



, so that, finally,

(,), (,)ufuvvguv==



(24.1.91''')

resulting an autonomous system. We return then to the plane

Oxy . To the critical points

(stable or instable) in the Van der Pol plane correspond cycles, in fact circles (stable or

instable, respectively) of radii

=+=+

22 22

ruv xy in the plane Oxy .

Let be, e.g., Duffing’s equation

+++ =

cosxxxx tαβγ δω  ,

(24.1.92)

equivalent to the system

MECHANICAL SYSTEMS, CLASSICAL MODELS

674

==−−−+

,cosxyy y x x tαβγ δω ;

(24.1.92')

making the change of variable (24.1.91), we obtain

() sin ( )sincos

(cos sin )sin ,

() sincos( )cos

(cos sin )cos .

uvutvtt

utvt t

vuuttvt

utvt t

ωβ α ω α δ ω ω

γω ω ω

ωβ α ω ω α δ ω

γω ω ω

=− − − +

+−

=− − − − +

+−



(24.1.93)

Averaging on the interval

[0, ], 2 /TT πω= , we get the system

()

=− − − +

=− − − − + −

() ,

28 2

uvuuuv

vuvvuv

γα

ωβ

γαδ

ωβ



(24.1.93')

the critical points being given by the equations

()

−−− +=

−++ ++=

() 0,

28 2

vu uuv

uv vuv

γα

ωβ

γαδ

ωβ

(24.1.93'')

together with the relation

22 2

, constuv AA+= = , corresponding to the limit

circles.

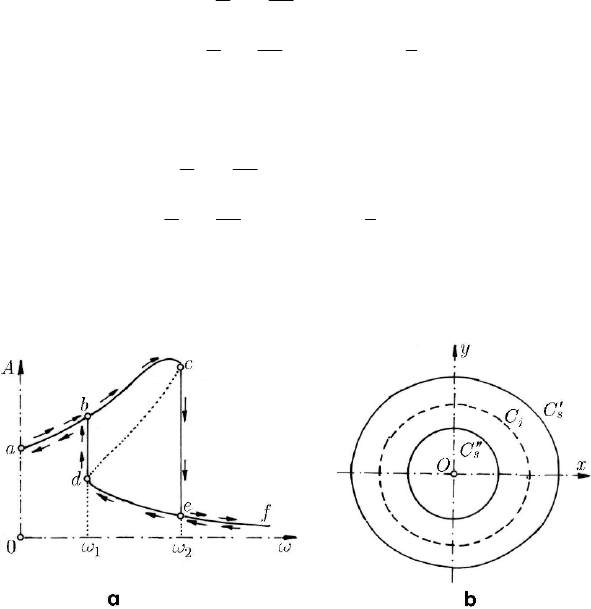
Fig. 24.11 Duffing’s equation: diagram A vs ω (a); Van der Pol’s plane (b)

Eliminating the variables

u and v between these relations, it results the equation

≡+ ++− −=

26 4 2 2 2

(,) 9 24 16[ 4( )] 16 0fA A A Aωγ γα αωβ γ ,

(24.1.94)

Dynamical Systems. Catastrophes and Chaos

675

where the relation between the amplitude

A and the pulsation ω is put in evidence;

representing the graphic of this implicit function in Fig. 24.11a, we see that for

≤<

0 ωω

and >

ωω there exists only one value of the amplitude A , for

, ωωωω== one obtains two such values, while for <<

ωωω there result

three values, two of them being stable and one instable. If the pulsation

ω increases,

beginning with

= 0ω , then the amplitude A follows the continuous line

abcef

, while

it the pulsation decreases, then the amplitude follows the continuous line

fedba ,

appearing two jumps; the broken line

cd corresponds to an instable situation. To the

critical points in Van der Pol’s plane correspond circles of radii

A in the plane

Oxy

(Fig. 24.11b). For

ω exterior to the interval correspond three circles: two stable circles

(

′

and

′′

) and an instable circle (

C ) (Fig. 24.11b). The instable cycle limits the

basins of attraction of the stable cycles, on this interval the dynamical system being

bistable.

24.1.3 Discrete Linear Dynamical Systems

Besides the continuous dynamical systems considered till now, we meet – in the

nature – also dynamical systems the evolution of which is not continuous, but discrete

in time. A phenomenon which can be thus modelled is, e.g., that of the populations, the

evolution of which is verified, by census, at certain intervals of time

After some general considerations, we will show, in what follows, how can be

adapted the notion of fixed point and we will make a study of the Poincaré

transformations, which put in evidence the passing from continuous to discrete motions.

24.1.3.1 General Considerations

Returning to the example mentioned above, let

, , ,...,

xxx x be the number of

individuals in a population after certain intervals of time; we put the problem to find a

law of evolution, hence of a law to link, e.g., the number

x (after n periods) to the

number

−1n

x (after − 1n periods). Such a law can be a relation of the form

−

( ), 1,2,...

xfx n ,

(24.1.95)

hence a recurrence relation or an application

f .

Eventually, we can imagine a relation of the form

−−

( , ), 2, 3,...

xfxx n ;

(24.1.95')

denoting

−

xy, the relation (24.1.95') is equivalent to the system of recurrence

relations

−− −

===

11 1

(,), , 1,2,...

nn n

xfxy yxn

(24.1.95'')

We can extend the relation (24.1.95') to a more general form, i. e.

MECHANICAL SYSTEMS, CLASSICAL MODELS

676

−

−−

==+

( , ,..., ), , 1,...

nnp

xfxx x npp ,

(24.1.96)

wherefrom, with the notations

, ,...

xyyz

−−

==, we obtain the system of

recurrence equations

111 1 1

( , , ,...), , ,..., 1,2,...

nnn

nnn n n

xfxyz yxzy n

−−− − −

====

(24.1.96')

In general, we can consider the system of recurrence equations

()

−−

11121

( ) ( ) ,( ) ,... , 1,2,...,

xfx x i  ,

(24.1.97)

which can be written in the matric form

−

=xx

()

f ,

(24.1.97')

where we have introduced the column vector

[,,..., ]

xx x .

24.1.3.2 Fixed Points

In concordance with the definition and the notation used in case of continuous

dynamical systems, we call fixed point of an application the point

∗

x for which

−

=xx

, hence for which

∗∗

=xx()f .

(24.1.98)

The significance of equilibrium of a fixed point remains – further – valid; in the case of

a population, it means that this one remains constant as number.

We can consider

f as an operator; in this case, let =

fff be the operator

defined by the composition relation

=xx

() (())fff

(24.1.99)

We notice that

∗∗∗∗

===xxxx

() (()) ()ffff

, so that

∗∗

=xx

()f

(24.1.99')

the fixed points of the operator

f being fixed points of the operator

f too. But the

operator

f can have also other fixed points besides

∗

x ; there exist thus the fixed

points

∗∗

x , distinct from

∗

x , for which

∗∗ ∗∗ ∗∗ ∗∗

=≠xxxx

() ,()ff.

(24.1.99'')

If the points

∗∗

x are real, they correspond to a periodic behaviour of period 2 . In the

case of a population, the number of the individuals does not remain constant, but

returns to the initial number by two to two intervals of time.

Dynamical Systems. Catastrophes and Chaos

677

In general, we can define the operator

= ...

fff f , which can have a fixed

point

∗∗ ∗

...

distinct from the previous ones, for which

∗∗ ∗ ∗∗ ∗

=xx

... ...

()

f ;

(24.1.100)

in this case,

f is a periodic application of period p .

Returning to the significance of equilibrium of the fixed point

∗

x , we can put the

corresponding problem of stability. Thus, if

f is analytic, an expansion in Taylor series

allows us to write (we consider now only one recurrence equation)

∗∗∗

′

+= + +

xxx

( ) () () ()fhf hf hO ,

(24.1.101)

where

()hO indicates the order of magnitude of

h . Keeping only the first two terms

of the expansion and taking into account (24.1.99'), we may write

∗∗∗

′

+≅+

xxx() ()fh hf;

(24.1.102)

applying once more the operator

, it results

()( )

[

]

( ) ( ) () () () ()fhffhfhf f hff

∗∗∗∗∗∗∗

′′′

+= + ≅ + ≅ +

xxxxxxx,

wherefrom

[]

∗∗ ∗

′

+≅+xx x

() ()fh hf

(24.1.102')

By the successive application of the operator

f , it results

[]

∗∗ ∗

′

+≅+xx x

()

() ()

fhhf

;

(24.1.102'')

if and only if

∗

′

x|()|1f , we get

∗∗

→∞

+=xx

()

lim ( )

;

(24.1.102''')

the position

∗

=xx being thus stable.

Let us suppose that

∗

=x 0 . If () 1f

∗

′

<−

x , then the equilibrium is instable, the point

x being far removed from the origin (which is thus a repeller); the succession of the

positions of the points is thus alternating. If

∗

′

=−

x() 1f , then the equilibrium is stable at

the limit, the succession of the points is alternating, but the points remain at the distance

from the origin. If

∗

′

−< <

x1()0f , then the equilibrium is asymptotically stable, the

succession of the points being alternating and approaching the origin. If

∗

′

x() 0f , then

the point remains at

O , the equilibrium being stable. If

∗

′

x0()1f , then the position

of equilibrium is asymptotically stable, the succession of the points being in one sense of

MECHANICAL SYSTEMS, CLASSICAL MODELS

678

the

Ox -axis, the negative one, and tending to zero. If

∗

′

x()1f , then the equilibrium is

simply stable, the points remaining at a fixed distance

h from the origin. If

∗

′

x()1f ,

then the equilibrium is instable, the succession of the points being in one sense of the

Ox -axis, namely the positive one, moving away from O .

24.1.3.3 Discretization in Time. Poincaré’s Transformation

To pass from a continuous in time dynamical process to a discrete one, one considers

the vector

x()t at equal intervals τ of time (eventually, sufficiently small); the

continuous function

∈x()

t  is replaced by the discrete function x

()t ,

(),(),...tt where

, 1,2,...

ttkkτ=+ =

To study such a problem, we use the

stroboscopic method, by a recurrence relation of the form

()

() ( ), 1,2,...

tft k

−

==xx .

(24.1.103)

As an example, let us consider a forced vibration which, after a transitory period,

tends to a harmonic vibration

=() cosxt a tω ; in Fig. 24.12a is indicated a

discretization, while in Fig. 24.12b one obtains

+()xt τ as a function of ()xt ,

joining by a continuous line the points

−1

(),()

xt xt given by the stroboscopic

method. Denoting

Fig. 24.12 The stroboscopic method: forced vibrations tending to harmonic

vibrations (a);

()xt τ+

()xt

diagram (b)

=+= −( ) cos ( ) (cos cos sin sin )yt a t a t tωτ τω τω

and eliminating the time

t between ()xt and ()yt , we find the equation of an ellipse

−

222

(cos )

sin

;

hence, the mentioned continuous line tends to this ellipse, which is a stable limit cycle.

We notice that, using the stroboscopic method, by passing to the discrete system of

recurrence equations, we remained in a space with the same number of dimensions.

Dynamical Systems. Catastrophes and Chaos

679

H. Poincaré has introduced another method of discretization in which the dimension of

the system thus obtained is with a unit smaller than of the initial system. Let be a

trajectory

C in a n -dimensional space of the dynamical system and a

(

− 1n )-dimensional hypersurface Σ

( , ,..., ) 0

gx x x ,

(24.1.104)

so that, at the points

∩C Σ , the trajectory be transverse (not orthogonal) to it. In case

of the dynamical system

=∈xxx(),



 ,

(24.1.105)

x()f is, obviously, a vector tangent to the trajectory at each point of it; the

transversality condition will be written, by means of the scalar product, in the form

⋅≠( ) grad 0fx g ,

(24.1.105')

the components of the gradient being

/ , 1,2,...,

gxi n∂∂ = .

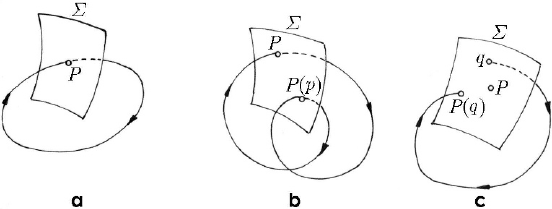
Fig. 24.13 Intersection of an orbit C with a hypersurface Σ:

periodic case (a,b); non-periodic case (c)

If the orbit is periodical, then the trajectory

C returns to the piercing point p with

the hypersurface

Σ , crossing it in the same sense (Fig 24.13a); as well, in the case of a

periodic orbit, it is possible that the trajectory, which starts from the piercing point

p ,

does cross a second time the surface at the point

≠()Pp p, returning then to p a.s.o.

(Fig. 24.13b). Obviously, the surface can be pierced several times too. Such solutions

are called subharmonics. If the orbit is not periodical, starting from the point

p one

can reach the point

, then the point ()Pq a.s.o., never returning at

(Fig. 24.13c).

To make some considerations concerning the orbital stability of a periodic solution,

we will admit that the motion takes place in a three-dimensional space, the surface

being pierced at a single point

. A perturbed motion is no more – in general –

periodical, the surface

Σ being pierced at the points

, ,...qq ; if these points tend to

p , then the periodic motion is orbital stable (asymptotically stable), otherwise being

orbital instable. If the points

, ,...qq remain in the neighbourhood of the point p ,

without tending to it, then the periodic motion is orbital simply stable. Thus, Poincaré

MECHANICAL SYSTEMS, CLASSICAL MODELS

680

has reduced the problem of the orbital stability of a trajectory in

 to a simpler one,

i.e. to the problem of the stability of a position of equilibrium, in fact of a fixed point of

an application in

 .

Fig. 24.14 Poincaré transformation

Let be a neighbourhood

⊆U Σ of the point p at which the trajectory C pierces

the surface

Σ , transverse to it. The first returning q of the trajectory in U , is called

the Poincaré transformation

→:PU Σ , defined by the relation

== ∈() (),qPp pqU

Φ ,

(24.1.106)

where

()qττ= is the time necessary to the point which, starting from

attains

; if

≡qp

, then the motion is periodical, of period τ . We notice that

is a fixed point of

the transformation, for which

= ()pPp.

(24.1.106')

It is convenient to choose a surface

Σ which divides the space in two regions, so

that the trajectory does pierce it in a great number of points (Fig. 24.14); the set of

these points forms the Poincaré transformation.

Fig. 24.15 Poincaré transformation of a one-dimensional non-autonomous system

Dynamical Systems. Catastrophes and Chaos

681

If the system of

n differential equations is non-autonomous, we can choose the

change of variable (24.1.2), obtaining an autonomous system of

+ 1n differential

equations in the cylindrical space

S

; let be the surface

{( , ) ; }

xSΣθ θθ=∈×=

. After each period T , the orbit x()t pierces Σ ; the

resulting transformation

→→:( )

P ΣΣ, hence the transformation

→+xx() ( )ttT is a Poincaré transformation. In Fig. 24.15 we put in evidence a

Poincaré transformation of a one-dimensional non-autonomous system.

Fig. 24.16 Graphic analysis of a Poincaré application: attractor (a); repeller (b)

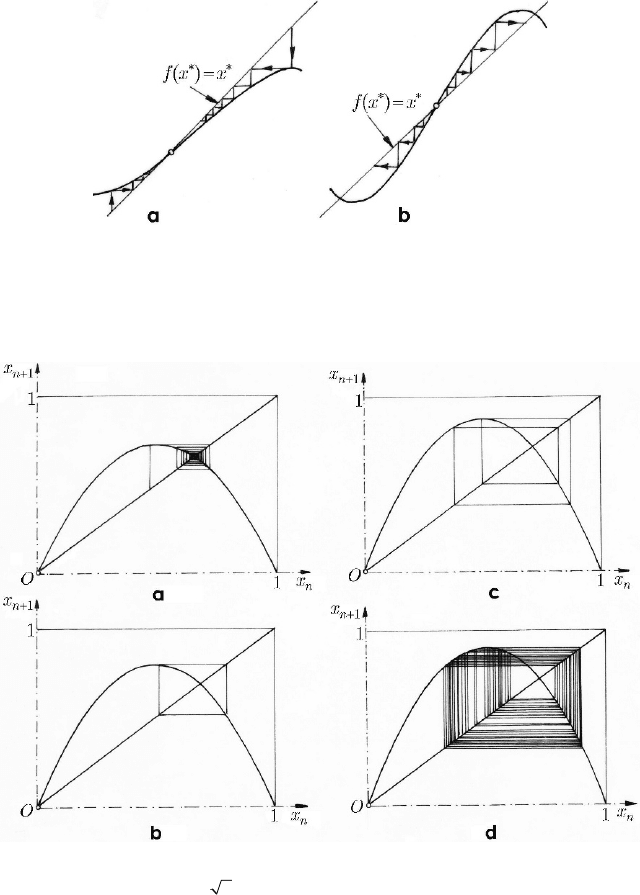
Returning to the fixed points which verify the relation (24.1.98), we have seen in the

preceding subsection the conditions which must be verified by

∗

′

x()f so as to have an

attractor or a repeller.

Fig. 24.17 The quadric logistic equation: attractor (

13a<<

) (a); bifurcation

( 316a≤<+ ) (b); a increasing (c); chaotic regime (d)