Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

642

where

123

III (condition of stability) are the principal moments of inertia.

Hence, the angle has a harmonic oscillatory motion of period

21 21

0.57736

3( )

pII II

ππ

== ≅

−−

(24.1.21')

where

2/T πω is the period of motion of the mass centre O on the trajectory.

The stability characteristics of the

Ox -axis can be improved (e.g., to maintain the

direction of a connection radio antenna) by introducing a moment, linear function of

and



; one obtains the differential equation

+=−−+

()pggvtθθ θθ

 



(24.1.22)

()vt being a perturbation. With the notations

, xxθθ==



, there results the system

of differential equations

()

==−+−+

122 1 122

,()xxx gpxgxvt ;

(24.1.22')

the matrix

⎡

⎤

⎢

⎥

−+ −

⎢

⎥

⎣

⎦

()gp g

has the characteristic equation

()()

ggp

gp g

ρρ

−

⎡⎤

=+ ++=

⎢⎥

−+ −+

⎢⎥

⎣⎦

Viète’s relations lead to

112 2 12

,()gpgρρ ρ ρ=− =−+

(24.1.22'')

so that we can choose, correspondingly, the vector

[, ]gg so as the roots have a

negative real part (

+> >

0, 0gp g ).

24.1.1.3 Non-autonomous Linear Systems of Differential Equations with Periodic

Coefficients. Floquet’s Theory

Let be the system of non-autonomous differential equations

=∈xAxx(),





(24.1.23)

Dynamical Systems. Catastrophes and Chaos

643

where

A is a square matrix of order n , the elements of which are continuous and

periodical functions in

t , of periodic T , so that

+= ∈AA()(),tT tt  ;

(24.1.23')

we add the initial conditions

=∈xxx

(0) ,

 .

(24.1.23'')

We choose the solution of the equation (24.1.23) in the form

=xx

() ()ttΦ ,

(24.1.24)

where the fundamental matrix

()tΦ verifies the condition = I(0)Φ , I being the unit

matrix; introducing in (24.1.23), we see that

()tΦ must satisfy the matrix differential

equation

= A() () ()ttt



ΦΦ,

(24.1.24')

for any initial conditions.

()tΦ is a fundamental matrix of the differential equation (24.1.23), then it is

almost evident that

+()tTΦ is such a matrix too and that

+= C()()tT tΦΦ,

(24.1.25)

where

C is a non-singular square matrix of order n .

Floquet showed that the fundamental matrix

()tΦ can be expressed in the form

P() ()e

ttΦ ,

(24.1.26)

where

P()t is a periodic square matrix ( +=PP()()tT t) of order n , while B is a

constant square matrix, of order

n too. Making the change of function

=xPy()t

(24.1.27)

and replacing in (24.1.23), we see that the column vector

[ , ,..., ]

yy y

verifies

the differential equation

=∈





yByy ;

(24.1.27')

thus, starting from a non-autonomous system, we have obtained an autonomous system

of differential equations.

MECHANICAL SYSTEMS, CLASSICAL MODELS

644

To study the stability of the solutions, Floquet assumes that

+= ∈() (),tT ttλ ΦΦ,

(24.1.28)

λ being a constant scalar; making, successively, = 0, ,2 ,...,tTTnT, we get

====xxx x

0000

(2 ) (2 ) ( ) (0)TT tλλλΦΦΦ

a.s.o.; by complete induction, we obtain, finally,

=xx

()

nT λ .

(24.1.28')

<||1λ , then →x()nT 0 for →∞n , the position of equilibrium

=x 0

being

stable; if

>||1λ , then ()nT →∞x for

→∞n

, while the position of equilibrium

=x 0 is instable. By writing the relation (24.1.28) for = 0t , we determine the values

λ ; we get thus

[

]

()t λ−=Ix 0Φ .

(24.1.29)

This homogeneous system of linear algebraic equations admits non-trivial solutions for

if and only if

[

]

−=Idet ( ) 0t λΦ .

(24.1.29')

The matrix

()tΦ is called matrix of monodromy and the eigenvalues = e

λ are

characteristic multipliers, the numbers

=, 1,2,...,

inρ , being characteristic

exponents. The stability takes place if, in modulus, no one of the characteristic

multipliers is supraunitary.

A non-autonomous differential equation with periodic coefficients is Mathieu’s

equation

()

++ =2cos2 0xtxγδ ,

(24.1.30)

where

γ and δ put in evidence the properties of the dynamical system; a mechanical

system which leads to such an equation is, e.g., the mathematical pendulum for which

the length of the thread is a harmonic function of time (

cosll a tω ). The study of

this equation can be made by means of Mathieu’s functions. In the following, we make

a study of the stability of the solutions of Mathieu’s equation as functions of the

parameters

γ and δ .

If the real part of the roots of the characteristic equation is negative, then the

configuration of equilibrium is stable; while if this part is positive, at least partially, the

respective configuration is instable; finally, if the roots are purely imaginary, then the

Dynamical Systems. Catastrophes and Chaos

645

solution is periodical. We search the conditions which must be fulfilled by the

parameters

γ and δ , so as to have limit solutions between the stable and the instable

ones.

Representing a periodic solution by a Fourier series

()

∞

∑

() cos sin

xt a nt b nt

(24.1.31)

replacing in (24.1.30), equating to zero the coefficients of the terms in

cosnt and

sin , 1,2,...nt n =

, and taking into account simple trigonometric relations as

++ −=

cos( 2) cos( 2) 2 cos cos2 ,

sin( 2) sin( 2) 2 sin cos2 ,

nt nt ntt

we may write

()

−+

−+ + =

+− + =

10,

22 0,

................................................

.................................................

aaa

anaa

γδ

γδδ

δγ δ

(24.1.32)

()

−+

−− + =

−+=

+− + =

10,

20,

................................................

.................................................

bnbb

γδδ

γδ

δγ δ

(24.1.32')

We notice that both homogeneous linear algebraic systems (24.1.32), (24.1.32') in the

unknowns

, , 0,1,2,...

ab i= , are decomposed in two subsystems, as the indices are

even or odd. To have non-trivial solutions, the four determinants of the coefficients of

each subsystem must vanish

−

Δ= =

−

000

200

040

00 6

γδ

δγ δ δ

δγ δ

…

…… … ………

(24.1.33)

MECHANICAL SYSTEMS, CLASSICAL MODELS

646

−+

−

Δ= =

−

1000

300

050

00 7

γδδ

δγ δ

…

………………

(24.1.33')

−−

−

Δ= =

−

1000

300

050

00 7

γδδ

δγ δ

…

………………

(24.1.33'')

−

Δ= =

−

2000

400

060

00 8

γδ

δγ δ

…

………………

(24.1.33''')

Taking a sufficient great number of lines and columns, we obtain, in a

(,)γδ -plane,

curves which separate the hatched stability regions of those of instability (Fig. 24.7).

We notice that, for

0δ → , the instability takes place for

222

0,1,2,3,...γ

; as δ is

greater, as a parallel to

Oγ meets smaller zones of instability. This graphic

representation is known as Strutt’s diagram.

Fig. 24.7 Strutt’s diagram for Mathieu’s equation

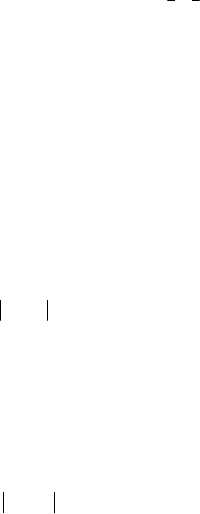
Dynamical Systems. Catastrophes and Chaos

647

Let us consider now another non-autonomous system of differential equations of the

from

[

]

=+xA Bx()t



(24.1.34)

where

and

are square matrices of order n , the latter one being constant; as one

can notice, if we make

=B 0 , then we find again the system (24.1.23).

Let us suppose that we have the estimation

Φ≤ +ΦΨ

∫

() () ()()d

tct τττ,

(24.1.35)

where

>() 0ct is a function of class

C , while () 0, () 0ttΦ>Ψ> are functions of

class

C , integrable on the interval

[, ], 0, consttt a a a+>=; we can state

Lemma 24.1.1 (Gronwall). The inequality

∫

′

Φ≤ +

∫

()d

() ( )e ( )e d

tct c

ττ

(24.1.35')

takes place in the conditions of the estimation (24.1.35).

In particular, if

==() constct δ , then the inequality (24.1.35') becomes

∫

Φ≤

()d

() e

ττ

δ .

(24.1.35'')

These inequalities are known as Gronwall’s inequalities.

A necessary (but not sufficient too) condition that the solution of the differential

equation (24.1.34) tend the solution of the equation

=xBx



→∞

=Alim ( )

t 0 .

(24.1.36)

Using the Lemma 24.1.1, we can state:

Theorem 24.1.2 If

Re 0, 1,2,...,

knλ ≤=

, hence if the real parts of the eigenvalues

of the matrix

B are non-positive, the purely imaginary eigenvalues being distinct, and

if the integral

∫

()dττ

(24.1.36')

is bounded, then the solution of the matric differential equation (24.1.34) is bounded

and the solution

=x 0 is stable.

Theorem 24.1.3 If Re 0, 1,2,...,

knλ <= , hence all the eigenvalues of the matrix

are negative and if the condition (24.1.36) holds, then the configuration of

equilibrium

=x 0 is asymptotically stable.

MECHANICAL SYSTEMS, CLASSICAL MODELS

648

24.1.2 Non-linear Differential Equations and Systems of Non-linear

Differential Equations

After some general considerations, we present, in what follows, various methods of

integration of the non-linear differential equations and of the systems of non-linear

differential equations; we will use thus both analytical and numerical methods of

calculation.

24.1.2.1 General Considerations

The non-linear properties of a material, the existence of geometric non-linearities,

the existence of free plays between the elements which form a dynamical system, the

existence of some non-linear limit conditions, the existence of a non-linear damping,

the existence of elements which contain fluids and many other causes lead – by their

mathematical modelling – to non-linear differential equations. Some characteristic

phenomena appear in this case. Thus, to periodic inputs – unlike the case of linear

systems for which the exits are periodical too, with the same period – the exits can be

periodical, having another period, can appear jumps (sudden variations) of amplitude or

of frequency, known as catastrophes, as well as some phenomena of sudden loss or

gain of stability.

Let be a non-linear differential equation of first order written in an implicit form

=(; , ) 0Ftxx .

(24.1.37)

If the conditions imposed by the theory of implicit functions are fulfilled, then we can

write

(; )

xftx



(24.1.37')

where we supposed that the point

(; )tx belongs to an open subset Ω of

 ; to solve

the solution (24.1.37) means to find all its solutions and to study their behaviour. We

call solution or integral curve or – shortly – integral of the equation (24.1.37) any

continuous and differentiable function

= ()xtϕ , definite on an open interval I , which

satisfies the relation

() (; ()), tftt xIϕϕ

′

=∀∈, if – supplementary – the points

(; ())ttϕ belong to Ω for any ∈tI.

The solution of the Cauchy problem associated to the equation (24.1.37') means the

determination of the solutions

()xt for which

()xt x,

(24.1.37'')

where

(; )tx is a given point in Ω . In certain convenient hypotheses on f , the

Cauchy problem for the equation (24.1.37') admits at least one solution; the uniqueness

of the solution is ensured if

f satisfies certain supplementary conditions.

Let us define, at any point

(; )Ptx of the domain Ω , the angle α by the formula

Dynamical Systems. Catastrophes and Chaos

649

=tan ( ; )ftxα .

(24.1.37''')

The point

(; )Ptx together with the angle α forms a so – called element of contact (or

linear element) (Fig. 24.8); the set of all the elements of contact is called field of

directions and defines the differential equation (24.1.37'). Hence, a solution or an

integral curve of the equation (24.1.37') is a curve which has a tangent at any point of it,

with the property that any of its elements of contact belongs to the corresponding field

of directions.

Fig. 24.8 Linear element of a non-linear differential equation of first order

For instance, to a geometrical determination of the integral curves of the equation

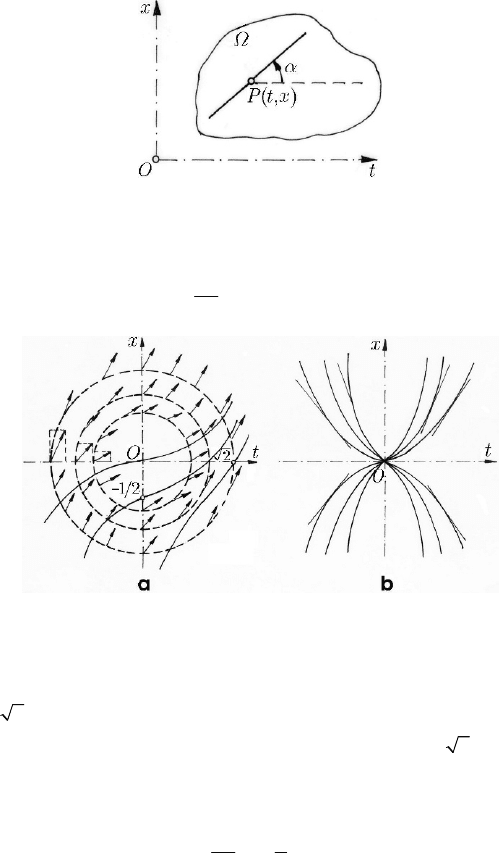
Fig. 24.9 Isoclinal lines for two differential equations

we draw, firstly, the curves for which the inclination is the same, called isoclinal lines.

Thus, for

0, 1/2, 1xx x== =  we obtain the centre

and two concentric circles

of radii

1/ 2

and 1 as inclinal curves. These curves are drawn in Fig. 24.9a, as the

integral curves which pass through the points

(0,0), (0, 1/2), ( 2,0)− ; the family of

integral curves thus obtained depends on a parameter. In Fig. 24.9b is represented the

field of directions corresponding to the equation

MECHANICAL SYSTEMS, CLASSICAL MODELS

650

formed by the tangents to the parabolas

, constxCtC==.

There are many possibilities to study the existence and uniqueness of the Cauchy

problem for the equation (24.1.37'), according to the functional frame in which the

calculation is made. It is necessary to introduce the notions of maximal solution and of

Lipschitz property to can state the classical theorem of existence and uniqueness.

(), xttIϕ=∈, is a solution of the equation (24.1.37), then – obviously – the

restriction of

ϕ to any subinterval of I is, as well, a solution. This remark allows the

introduction of an order relationship on the set of the solutions of (24.1.37); more

precisely, if

(), ttIϕ ∈ , and

(), ttIϕ ∈ , are two solutions, then we say that

()tϕ is “smaller” than

()tϕ and we write

ϕϕ≺ if ⊂

II and =

() ()ttϕϕ

for any

∈

tI. In fact,

ϕϕ≺ means that

ϕ is the prolongation of

ϕ . Any

maximal element of the set of solutions is called maximal solution. According to this

definition, such a solution can no more be prolonged in

Ω ; one can also prove that any

solution is “smaller” than a certain maximal solution.

We say that the function

(; )ftx is Lipschitzian with respect to x if one can find a

constant

> 0K , called Lipschitz’s constant, such that

−<− ∈Ω∈Ω

12121 2

( ; ) ( ; ) ,( ; ) ,( ; )ftx ftx Kx x tx tx .

(24.1.38)

The function

(; )ftx is called locally Lipschitzian if any point of Ω has a

neighbourhood on which

f is Lipschitzian. There are large classes of functions with

Lipschitz’s property, e. g., the analytic functions and, in general, the functions of

bounded derivatives with respect to

x are also Lipschitzian.

A function

f may be Lipschitzian in x without being continuous with respect to

(; )tx . Indeed, let =+(; ) ()ftx gt x; this function is obviously Lipschitz with respect

x , independently of the continuity of g .

Let us also note that a locally Lipschitz function is not necessarily Lipschitz on the

whole domain of definition; let us take

(; ) , (; )ftx x tx==Ω= , as

counter-example.

We can state

Theorem 24.1.4 Let (; )ftx be defined and continuous on the open set Ω⊂

 and

locally Lipschitzian in

x . Then there is a unique maximal solution of (24.1.37) passing

through any arbitrary point of

Ω .

In what concerns the Cauchy problem, the (local) existence and the uniqueness of the

solutions are ensured by

Theorem 24.1.5 (Cauchy, Picard, Lipschitz). If the function (; )ftx is continuous with

respect to the variables

t and x in a rectangle D , centred at

(; )tx , and is

Lipschitzian in

D , then it exists only one integral curve of the equation (24.1.37)

which passes through the point

(; )tx .

f is only continuous in D , then one can ensure only the existence of the solution

(the Cauchy–Peano theorem), but the uniqueness may fail.

Dynamical Systems. Catastrophes and Chaos

651

The proof of this theorem is constructive, being based on the method of successive

approximations, also called the Picard-Lindelöff method (see Sect. 24.1.2.2).

Among the differential equations which can be easily integrated, we mention: the

differential equations with separate (or separable) variables, the homogeneous

differential equations, the total differential equations, as well as the equations which

may be brought to such a form by means of an integrant factor. We mention also some

non-linear differential equations of a special form, i.e.: Clairaut’s equation

=+()xtx xϕ,

(24.1.39)

Lagrange’s equation

++=() () () 0Axx Bxt C x,

(24.1.39')

Bernoulli’s equation

++ =

() () 0xPtxQtx

(24.1.39'')

and Riccati’s equation

=+ +

() () ()xPtxQtx Rt ;

(24.1.39''')

there exist specific methods of integration for all these equations.

The general form of a non-linear differential equation of second order is

=(; , , ) 0Ftxxx ;

(24.1.40)

∂∂≠/0Fx on the domain of definition of F and if F is sufficiently regular, then,

by the implicit function theorem, we can obtain

x explicitly, thus getting the normal

(canonic) form

(; , ), :

xftxxfI=××→ DD .

(24.1.40')

One can associate to the equation (24.1.40'), in a natural form, initial conditions of

the form

==∈⊂

00000

() ,() ,xt x xt x x I ,

(24.1.41)

which are conditions of Cauchy type; in this case too, one can prove a theorem of

existence and uniqueness, similar to the Theorem 24.1.5.

We have seen that, in Cauchy’s problem (24.1.40), (24.1.40'), the values of the

unknown function and of its derivative are supposed to be known for a same moment

. But there exist problems which need another mathematical model, e. g., those in

which one knows the values of the function at two moments

and

; the most simple

conditions of this type are