Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

622

⎛⎞ ⎛⎞

+−=−++=

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

12 1 2

11 1 1

0, 0

kk k k

CC C C

II I I

λλ;

the characteristic equation

+−

⎛⎞

=+ + =

⎜⎟

⎝⎠

−+

kk II

λλ

has a double root equal to zero and two imaginary roots

=±

1,2

iλω,

(1/ 1/ )kI Iω =+.

Finally, we obtain the solution

=+ + − =+ − −

cos( ), cos( )

ABtC t ABtC t

θωϕθ ωϕ

(23.2.100')

Hence, the motion is formed by a uniform rotation over which is superposed a harmonic

oscillatory motion. The ratio of the amplitudes of these oscillations is

−=−

12 1

/( / ) /

CCII II; hence, there exists a point in the interior of the segment of

a line

AA , determined by this ratio for which the amplitude vanishes during the

motion, the respective cross section of the axletree having only a uniform motion.

23.2.4.5 The Dynamical Absorber

Let be a discrete mechanical system with one degree of freedom, modelled by a mass

M , which is linked to a spring of elastic characteristic K and is in resonance under the

action of a perturbing force

cosFF tω ; let us suppose that the proper pulsation

= /pKM in equal to the pulsation ω of the perturbing force. Let us link a mass m

to the mass

M by a spring of elastic constant k , so that =//KM km; m and k

may be very small with respect to

M and K respectively (Fig. 23.26). The discrete

mechanical system becomes thus a system with two degrees of freedom, and the mass

M , as we will show, does no more vibrate.

Fig. 23.26 Dynamical absorber

The equations of motion of the new discrete mechanical system are

1121

221

()cos,

(),

Mx Kx k x x F t

Mx k x x

ω=− + − +

=− −



(23.2.101)

Stability and Vibrations

623

or, in a matric form,

+−

⎡⎤

⎡⎤ ⎡⎤

⎡⎤

⎢⎥

⎢⎥ ⎢⎥

⎢⎥

−

⎣⎦

⎢⎥

⎣⎦

⎣⎦ ⎣⎦

⎣⎦

cos

xKkkx



(23.2.101')

as a real part of the matric equation

+−

⎡⎤

⎡⎤ ⎡⎤

⎡⎤

⎢⎥

⎢⎥ ⎢⎥

⎢⎥

−

⎣⎦

⎢⎥

⎣⎦

⎣⎦ ⎣⎦

⎣⎦

zKkkz



(23.2.101'')

Searching solutions of the form

−

()i

ωϕ

, for which +=

0zzω , one obtains,

for the real part,

()

[]

{}

()

[]

{}

−

−++ +

()cos

cos

;

km F t

Mm Km k M m Kk

kF t

Mm Km k M m Kk

ωω

(23.2.102)

if one takes into account the conditions imposed to the masses and to the elastic

constants, then it results

==−

0, cos

xx t

(23.2.102')

the effect of resonance being thus avoided (the amplitude of the mass

M vanishes).

One has thus obtained a dynamical absorber without damping.

We notice that the amplitude of the vibrations of the additional mass can be very

great if the ratio

/Fk is also very great. On the other hand, the vibrations of the

additional mass are in phase opposition (due to the sign minus) with the perturbing

force; thus, it results the relation of equilibrium between the tension in the additional

spring and the perturbing force (

cos 0kx F tω ), which justifies the performance

of the dynamical absorber.

If the pulsation

ω of the perturbing force is not maintained constant, then the

phenomenon of resonance can no more be avoided. Thus, let us consider the

denominator of the expressions (23.2.102), divided by the product

Mm of the masses;

it results

()

=− + +

42 24

() 2

fpp

ωω ω ,

(23.2.103)

where we have introduced the proper pulsation given by

//pKMkm. We

notice that

±∞ = ∞()f , =− <

() ( / ) 0fp k Mp ; it results that the equation

=() 0f ω has two real roots, contained in the intervals −∞ ∞(,),(,)pp . If the ratio

MECHANICAL SYSTEMS, CLASSICAL MODELS

624

/km is small, then the roots are close to = pω , while for = pω we have =

0x ;

the diagram of the displacement

()xxω has two vertical asymptotes (Fig. 23.27).

=/0kM , then one has a double root

= pω

, remaining only one vertical

asymptote, as in the classical phenomenon of resonance. One obtains the static

displacement

/xFK for = 0ω .

Fig. 23.27 Displacement diagram

x vs ω

To avoid the phenomenon of resonance mentioned above, we must introduce –

beside the additional mass – a damper too.

The model of the mechanical damper considered above (Fig. 23.26) can be

completed by a viscous damper of constant

′

(Fig. 23.28). The corresponding system

of differential equations is of the form

Fig. 23.28 Mechanical and viscous damper

′

=− + − + − +

′

=− − − −

1121 21

22121

()()cos,

()(),

Mx Kx k x x k x x F t

mx k x x k x x

ω  

  

(23.2.104)

as a real part of the system (

==−==−

111 1222 2

i, , i,zzz zzzz zωωωω   )

Stability and Vibrations

625

′′

+− + − +

⎡⎤

⎢⎥

′′

−+ − +

⎣⎦

⎢⎥

⎣⎦

i(i)

(i) i

KkM k k k z

kk km k

ωω ω

ωωω

(23.2.104')

written in a matric form. We get thus

()

()()

()

′

=−+

′

=+− − −+−+

⎡⎤

⎣⎦

222 2

ie,

zkmkF

zkkF

NKkM km k KMm k

ωω

ωω ωω

(23.2.104'')

the amplitude of the motion of the mass

M will be

()

()()

()

′

== − +

′

=+− −−+−+

⎡⎤⎡⎤

⎣⎦⎣⎦

max 2 2 2

222 222

xz km kF

NKkMkmkKMmk

ωω

ωω ωω

(23.2.104''')

Under the action of the constant force

raises the static deformation

/xFK; to study the dynamical influence, we introduce the non-dimensional

ratio

max st

/xxψ , given by

()

′

=−+

222

Kkm k

ψωω

(23.2.105)

Putting in evidence the terms which contain the damping, we may write

′

AAk

BBk

(23.2.105')

with

()

()()

()

=− =

=+− − −

⎡⎤

⎣⎦

=−+

⎡⎤

⎣

⎦

22 2

222

AKkm AK

BKkMkm k

BKMm

ωω

(23.2.105'')

We can write the relation (23.2.105') in the form

()

′

−+ − =

2222

1122

0BABAkψψω;

hence, the family of curves (23.2.104') passes through the points of piercing of the

curves

11 22

0, 0BA BAψψ−= −=, hence of the curves

MECHANICAL SYSTEMS, CLASSICAL MODELS

626

()()

()

222

Kk m

KkM km k

KMm

ωω

−

+− − −

−+

(23.2.105''')

The curve

()ψψω corresponds to the dynamical absorber without damping

(

′

= 0k

) and the curve =

()ψψω corresponds to the discrete mechanical system

with only one degree of freedom, of mass

+Mm and constant K (the masses are

rigidly linked, corresponding

′

=∞k

, =+

/( )KMmω ); the two curves are

piercing at the points

and Q , through which passes any curve = ()ψψω

(Fig. 23.29).

Fig. 23.29 The curves ()ψω vs ω

Starting from these data, we must search the best additional mass

m , the best elastic

coefficient

and the best damping coefficient

′

, so that the dynamic absorber with

damping does work in the best conditions. If the ordinate of the point

P is greater than

the ordinate of the point

Q , it is optional that this one be the maximal ordinate, the

tangent at

P being horizontal; on the other hand, it is recommended that the ordinate of

the point

be as small as possible. To realize such an optimum, one must choose

conveniently the parameters which are involved. We denote

′

== = = =

′

,,,2,

mK k k

ppkmk

MM m k

μχ

(23.2.106)

where

′

k in a critical damping coefficient, while χ is a non-dimensional damping

factor (see Sect. 8.2.1.3, formulae (8.2.14), (8.2.14')); after fastidious calculations, one

can show that an optimum corresponding to

Stability and Vibrations

627

== =+

13 2

,,1

8(1 )

χψ

μμ

(23.2.106')

function of the non-dimensional coefficient

μ , which specifies the mass m .

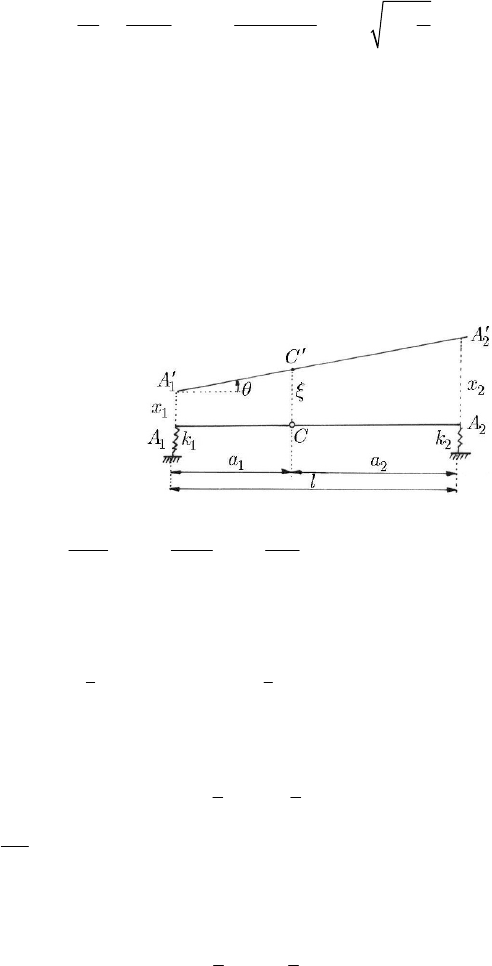
23.2.4.6 Oscillations of Vehicles

Let us model a vehicle of mass M by a rigid bar of length l , elastically supported at

A and

A , the corresponding elastic constants being

k and

k , respectively; the

centre of gravity

C is at the distances

a and

a from the support

A and

A ,

respectively (Fig. 23.30). We denote by

the moment of inertia with respect to an

axis normal to the plane of the figure at the point

C .

Fig. 23.30 Modelling of the oscillations of vehicles

Let

111222

, , xAAxAA CCξ

′′′

===

be the displacements of the extremities of the

bar and of the mass centre, respectively; we denote by

θ the angle of rotation of the bar

AA , supposed to be very small. We notice that

()()

21 12 2 1 1 2

,,ax ax x x l a a

ξθ=+ =−=+

(23.2.107)

The kinetic energy is expressed in the form (we apply Koenig’s theorem)

()

22 22

21 121212

CCC

TM I

Ma I x Ma a I x x Ma I x

ξθ=+

=++−++

⎡⎤

⎣⎦





(23.2.108)

while the potential energy is given by

11 22

Vkx kx

;

(23.2.108')

calculating the kinetic potential

=−TVL , we get Lagrange’s equations in the form

++= ++=

11 1 12 2 11 1 21 1 22 2 22 2

0, 0mx mx kx mx mx kx    ,

(23.2.109)

MECHANICAL SYSTEMS, CLASSICAL MODELS

628

where

()

=+ == +

=+====

11 2 12 21 1 2

22 1 11 1 12 21 22 2

,, 0,.

mMaImmMaaI

mMaIkkkkkk

(23.2.109')

We notice that the considered discrete mechanical system is dynamically coupled

(

=≠

12 12

0, 0km). But the maximum comfort is obtained when the mechanical

system is entirely uncoupled, hence if we have

0m too; imposing this condition,

we must have

Ma a I . Introducing the central radius of gyration (

iIM

we get the condition

iaa;

(23.2.110)

hence, the radius of gyration

i must be the geometric (proportional) mean of the

distances

a and

a from the centre of gravity of the vehicle to its points of suspension.

Chapter 24

Dynamical Systems. Catastrophes and Chaos

In 1776, ninety years after the apparition of the fundamental treatise of Newton,

Laplace enounces his famous principle of the determinism, stating that: “The actual

stage of the system of nature is, obviously, a consequence of that it was at the preceding

moment and, if we imagine an intelligence, which – at a given moment – knows all the

relations between entities of this universe, then it could establish the respective

positions and the motions of all these entities, at any moment in the past or in the

future” This determinism is – in fact – a mechanistic determinism. But Laplace

continues: ... “there exist things which are uncertain for us, things which are more or

less probable and we try to counter-balance the impossibility to know them,

determining various degrees of probability”. We are thus obliged, at a certain level of

knowledge, to accept also a probabilistic principle, which – by Laplace – depends on

the accuracy of the instruments of measure. Hundred thirty years later, in 1903, Henri

Poincaré observes that: “A very little cause, which escapes from our observation, can

lead to a sensible effect and then we say that the effect is due to the chance. It can

happen that small differences at the initial conditions do produce an enormous error in

what will be later. The prediction becomes thus impossible and we have to do with

unforeseeable phenomena”. As an example of the sensibility of the differential

equations to initial conditions, E.N. Lorenz, professor of meteorology, says: “If a

butterfly which stays today on a flower flaps or not its wings, that has not a great

influence on the weather in the following days, but – in exchange – can have a great

influence on the weather some years after.” This fact is known today as the Lorenz’s

butterfly effect.

The uncertainty principle of Heisenberg according to which the position and the

momentum of an elementary particle cannot be determined simultaneously with a

precision as great as we wish, the Brownian motion, characterized by a great number of

collisions between the particles of a very fine solid suspension in a liquid and its

molecules, and many other phenomena put in evidence the necessity to introduce

notions of the theory of probability as well as the aleatory variables. There appears

thus the notion of chaos; and if the chaotic motions are produced in deterministic

conditions, then there appears the notion of deterministic chaos, introduced forty years

ago by D. Ruelle and F. Takens, by describing some phenomena of turbulent flow. The

study of the causes which produce this paradoxical phenomenon introduces the notion

of attractor in various forms: punctual attractor, periodic attractor and chaotic strange

attractor (Arnold, V.I., 1984, 1988).

The geometric representation of the critical (ramification) points led René Thom, in

1972, to the notion of catastrophe, thus being developed the theory of catastrophes

(Thom, R., 1972).

629

P.P. Teodorescu, Mechanical Systems, Classical Models,

MECHANICAL SYSTEMS, CLASSICAL MODELS

630

The evolution of the systems in time is modelled, obviously, by non-linear

differential equations, for which solutions in analytical closed form can be only very

seldom obtained. Even if these systems have been – at the beginning – only mechanical

ones, they involved afterwards all the chapters of physics, chemistry, biology etc. To

integrate these systems, one uses – in general – numerical algorithms; but all the

problems mentioned above are put. Thus appeared the theory of dynamical systems,

which has been very much developed last years; we can say that it is a qualitative

theory of ordinary differential equations. Obviously, a dynamical system has a more

general significance than that of mechanical system, containing also electromagnetical,

biological, economical, social, political systems etc.

We present in this chapter continuous and discrete dynamical systems, for which we

put in evidence periodical solutions and global ramifications. We are thus led to

introduce some elements of catastrophe theory. In the theory of chaos (especially

deterministic chaos) we will use the notions of strange attractor, fractal etc.

24.1 Continuous and Discrete Dynamical Systems

The time has, in general, a continuous variation in the study of a dynamical system;

but one can consider also cases in which the results are obtained for discrete values of

the time variable. We will deal with both situations. As well, we make distinction

between linear and non-linear systems.

24.1.1 Continuous Linear Dynamical Systems

We introduce, in what follows, the most important notion necessary to the study of

dynamical systems, especially the notion of attractor. We mention also the study of

non-autonomous linear systems of differential equations with a control function or with

periodic coefficients.

24.1.1.1 Fixed Points. Attractors

Let be the non-autonomous system of differential equations with initial conditions

(of Cauchy type)

Xx x x

(;), ( )

(24.1.1)

where the column vectors

⎡

⎤

⎡⎤

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎣⎦

⎣

⎦



(24.1.1')

Dynamical Systems. Catastrophes and Chaos

631

belong to the space

 , while

∈t  (we suppose that t is non-negative). If the time

does not appear explicitly, then the system is called autonomous or dynamical, having

the form

Xx x x

(), ( )

(24.1.1'')

If, in this case, all the roots of the characteristic equation (see Sects. 23.1.1.5 and

23.1.1.6) have their real part non-zero (real or complex roots), then the dynamical

system is hyperbolic; if the characteristic equation has at least a root or a pair of roots

with a null real part (zero root or purely imaginary roots), then the dynamical system is

degenerate.

As well, if

(;) (; )ttT=+Xx Xx ,

(24.1.1''')

then the system is periodical of period

T . By a change of variable

θπ= ,

(24.1.2)

the periodic non-autonomous system of order

n is transformed in the autonomous

system of order

+ 1n

000

dd2

(;), , ( ) ,( ) 2

ttT T

θπ

θθπ

====

Xx x x

(24.1.2')

Hence, the dynamical system thus considered in the application

×→:

f  , definite by the solution ()tx ; a field of vectors is thus definite in

 .

We assume that the phase space is orthogonal, the co-ordinates corresponding to the

variables necessary to specify the state of a system at a given moment. For instance, in

case of a particle in motion in one dimension, the phase space is two-dimensional (the

canonical co-ordinates correspond to the position and to the velocity of the particle); in

general, Gibb’s space

is a phase space.

Let us consider the case of the non-damped linear oscillator (the harmonic oscillator)

(23.1.2), with the initial conditions

(0) , (0)qqqq==. We denote

, qxqx== ,

being led to the system of differential equations

200

211122

, , (0) , (0)

xxxxxx

ω==− = =;

(24.1.3)

the solution of this system is