Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

612

the Van der Pol equation becomes

−

−+=

()

ccx



(23.2.88'')

By the change of function

/xccz=

, the differential equation (23.2.88') takes the

form

()

−− +=

zzε

(23.2.88''')

with the notation

/ckmε

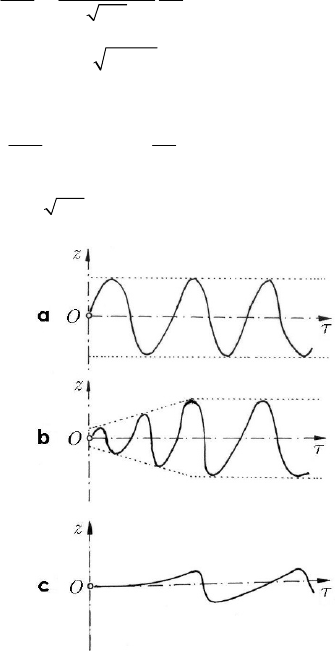
Fig. 23.21 Non-linear self - vibrations: (a) 0ε = ; (b) 0.1ε = , small; (c) 10ε = , great

The motion is very much influenced by the value of the parameter

ε . Thus, if

= 0ε , then the vibrations are harmonic, their graph being given in Fig. 23.21a. If the

values of the parameter are small (e. g.,

= 0.1ε ), then the motion has, at the beginning,

the character of self-vibrations, the amplitudes increasing very much; when the

amplitudes attain a sufficiently great value, then appears a phenomenon of limitation of

them, hence a phenomenon of saturation (Fig. 23.21b). If the parameter

ε is great (e.

g.,

= 10ε ), then appear the so called relaxation vibrations, characterized by slow

increases followed by sudden decreases of the elongation (Fig. 23.21c).

23.2.4 Applications

In what follows we present some applications to the results obtained in the case of

the linear vibrations. We consider thus two centrifugal regulators (one of them is the

Watt regulator), a mechanical system rotor-axletree, the vibrations of the axles of

Stability and Vibrations

613

negligible mass, the dynamical absorber without and with damping and the oscillations

of the vehicles.

23.2.4.1 Centrifugal Regulator of James Watt

A Watt centrifugal regulator is compound of two rods OA and OB of the same

length

l , hinged at the point O to a vertical axletree; at their ends one has two balls of

equal masses

m . Other two rods CD and CE are hinged at the points D and E to

the first ones and by a clutch

C , which slides along the axletree; one assumes that the

quadrangle is a rhomb of side

a . For the balls A and B is considered a particle

modelling (Fig. 23.22). If the angular velocity of the axletree increases, then the rods

and the masses raise; as well, the clutch raises, acting by a force

P the manoeuvre of a

system of levels which decrease the admission of the steam in a motor. The masses of

the rods and of the clutch are neglected.

Fig. 23.22 Centrifugal regulator of James Watt

The position of the regulator is determined, at a certain moment, by the angle of

rotation

of the plane of the regulator about the axle

and by the angle ϕ made

by the rods

OA and

with the axis of the axletree, in the plane of the regulator; the

discrete mechanical system has thus two degrees of freedom. The moment of inertia of

the parts in rotation (excepting the balls

A and

) with respect to the axis of the

axletree is

; the bringing back moment due to the variation

Δ= −

ϕϕϕ

of the

angle

ϕ (made by OA with

), with respect to an angle

ϕ , in case of a constant

angular velocity

ω of the axletree, is −Δ =− −

()kkϕϕϕ, where

is a constant

coefficient.

The motion of the regulator is composed of a rotation in its plane about an axis

normal at

to the plane, by the angular velocity

ϕ

and by a rotation of the plane

about the axis

OC , with the angular velocity



. The two axes are principal axes of

inertia, so that we obtain the kinetic energy

()

TII

θϕ



(23.2.89)

MECHANICAL SYSTEMS, CLASSICAL MODELS

614

with

=+ =

22 2

2sin, 2

II ml I mlϕ ;

finally, it results

()

=+ +

⎡⎤

⎣⎦

22 2 22

2sin 2

TIml mlϕθ ϕ



Upon the regulator act the weights

mg of the balls, the force P in the clutch. The

moment

−−

()k ϕϕ and the constraint forces at

and

, which give a vanishing

virtual work. Assuming that only a virtual displacement

δθ

takes place, we obtain

=− −

()Wkδϕϕδθ; it results the generalized force =− −

()Qk

ϕϕ.

As well, the virtual displacement

δϕ

leads to

δ=δ+ δ+ δ=δ+ δ2

CBC

W Pz mgz mgz Pz mgz ;

but

2cos, cos

za zlϕϕ==, so that 2( )sinWaPmglϕδϕδ=− + . It results the

generalized force

()

=− +2sinQaPmgl

ϕ .

We obtain thus Lagrange’s equations

()

∂

=− − − =− +

∂

,2sin

Ik I aPmgl

θϕϕϕθ ϕ



(23.2.90)

We search first of all the position of relative equilibrium of the regulator in its plane,

corresponding to a rotation with a constant angular velocity

θω



about the axis of

the axletree; let be

ϕ the angle corresponding to this position. Observing that = 0ϕ ,

the second equation (23.2.90) leads to

−− =

00 0

sin ( cos ) 0ml aP mglϕω ϕ ; one

obtains thus two positions of relative equilibrium: for

0ϕ and for

cos ( )/aP mgl m lϕω. The motion with a constant angular velocity

ω , given by

the second relation for which we assume that

aP mgl m lω , is called motion of

regime of the regulator.

We use now the equations (23.2.90) to study the small oscillations about this motion

of regime. We denote

, ϕϕ ψθω γ=+ =+



. The first equation (23.2.90) is

written in the form

()

+=−−

4sincosml I kϕϕϕθ θ ϕϕ





wherefrom

Stability and Vibrations

615

()() ()

++++ +=

⎡⎤

⎣⎦

222

00 0

2sin2 2sin

ml I ml kϕ ψψω γ ϕ ψ γ ψ



;

neglecting the powers of higher order (

sin , cos 1ψψ ψ≅≅

), we get

()

++ +=

22 2

000

2 sin 2 sin 2 0

Iml ml kϕγ ω ϕψ ψ



The second equation (23.2.90) becomes

()

−=−+

2sincos2 sinIml aPmglϕθϕϕ ϕ





()()

()

00 0

sin 2 sinIml aPmglψωγϕψ ϕψ−+ +=−+ +



(23.2.90')

In the frame of the same approximation, we obtain

−+=

0000

sin 2 sin 0ψω ϕγω ϕψ



(23.2.90'')

The solutions of the system of equations (23.2.90'), (23.2.90'') are of the form

e, e

λλ

ψγ==

and lead to the characteristic equation (the necessary and

sufficient condition that

A and

A be non-zero)

++=

0aaaλλ ,

(23.2.91)

where

=+ =

⎛⎞

=++=

⎜⎟

⎝⎠

22 2 2

00 0 00

sin , 0,

sin 1 3 cos , sin .

ml ml

ωϕ ϕ ωϕ

(23.2.91')

To have a stable motion, the real parts of the roots

λ must be negative. According to

Hurwitz’s criterion, this takes place if

()

>=−>

=−>

1123

23123

0, 0,

00;

aaaaa

aa aaa aa

(23.2.91'')

but, as it can be seen in the considered case, these conditions are not verified, the

motion of regime being instable. This fact – and it can be experimentally seen –

imposes the introduction of new elements in the system of regulations.

MECHANICAL SYSTEMS, CLASSICAL MODELS

616

23.2.4.2 Centrifugal Regulator

We will study the motion of the centrifugal regulator in Fig. 23.23. Each ball has the

mass

m and the clutch has the mass

m , the spring is of elastic constant

and the four

bars have each one the length

; the weights of the bars and of the spring are negligible.

The moment of inertia of the clutch with respect to the axis of rotation is

. Upon the axis

of the regulator acts a moment

, so that the regulator will rotate with an angular velocity

ω , the variation of which leads to a change of the distance of the balls from the axis of

rotation, to a displacement of the clutch and to a deformation of the spring; a device acts on

a valve which regulates the supply with fuel of the engine, so as to have a certain angular

velocity. We assume also that the clutch is linked to a hydraulic damper which produces a

viscous force of resistance, the damping coefficient being

c .

Fig. 23.23 Centrifugal regulator

We choose as generalized co-ordinates the angle

ϕ of the rotation about the vertical

axis and the angle

α , indicated on the figure; hence, the discrete mechanical system has

two degrees of freedom. We assume that the regulator is built up so that for

= 0α the

spring be non-deformed; the distances

s and

s , indicated on the figure, are measured

from this position of the clutch and are given by

(2 cos ) , 2(1 cos )sls lαα=− = − .

The kinetic energy of the balls and of the clutch, respectively, will be

==+

222

11222

222

TTmI

ννϕ .

Observing that, for the two balls, the relative velocities and the transportation

velocities are orthogonal and that

, ( sin )

vlv alααϕ==+, we get

=+ +

2222

(sin)val lαα . The clutch has a motion of rotation about the vertical axis

Stability and Vibrations

617

with the angular velocity

ϕ and a motion of rotation about the vertical axis with the

angular velocity

d/d 2 sinvstlαα . Finally, the kinetic energy of the discrete

mechanical system is given by

()

12 1

2222

2sin

24sin.

TTT mal I

ml ml

αϕ

αα

=+= + +

⎡

⎤

⎣

⎦



(23.2.92)

In a displacement compatible with the constraints, the virtual work is given by

δ = δ+ δ= δ− δ − δ − δ − δ

11 22 22 22

2WQ Q M mgs mgs kss css

ϕα

ϕαϕ  ,

where

is the elastic force in the spring and

cs

, in the viscous resistance.

Calculating

δδ

,ssand

s and replacing in the above relation, we may write

[

()

222

2sin2sin

4 1 cos sin 4 sin ,

WM mgl mgl

lk lc

ϕαα

αα ααα

δ=δ+− −

−− − δ

⎤

⎦



so that the generalized forces will be

()

[

()

]

, 2 sin 2 1 cos sin 2 sin .QMQ l mmglk lc

ϕα

ααααα==− ++− +

(23.2.92')

Lagrange’s equations are given by

() ()

()

[]

22 22

12 2

2 sin 4 sin cos ,

2sin 2 sincos

sin cos

sin 2 1 cos 2 sin

ma l I ma l l M

mm l ml

ma l l

lmmglk lc

αϕ αϕαα

αα α α α

αϕ α

αααα

++++ =

⎡⎤

⎣⎦

−+

=− + + − +

  

 



(23.2.92'')

and form a system of non-linear differential equations.

Obviously, the rôle of the regulator is to maintain a constant angular velocity

ω of

the axis. First of all, we will determine the position of relative equilibrium of the

regulator, corresponding to this angular velocity; the corresponding motion of the

regulator is the motion of regime. In this case, let

λ be the value of α and

constϕω== . Because = 0ϕ and = 0α , it results that = 0M and

() ()

()

00 0 0 0 0

1 12

sin cos 2 1 cos sin sin 0,ma l kl m mgαω α α α α+−−−+=

(23.2.92''')

MECHANICAL SYSTEMS, CLASSICAL MODELS

618

obtaining thus the connection between the angular velocity

ω of regime, the position

of the regulator and the position

=−

2(1 cos )slα of the clutch an important relation

for design. To put in evidence the stability of the motion of regime, we assume that this one

is characterized by

ω and can be perturbed by the variation of the moment M . We can

write

== +

ϕωω ω and =+

αα α, where

ω and

α are small, so that we can

consider

()

+= +

+= −

′′

+= + +≅

000

000 0

11 1

sin sin cos ,

cos cos sin ,

() ()... (),MMM M

αα αα α

αα α α α α α

because

()0M α .

Replacing in the differential equations (23.2.92'') and taking into account the

equation (23.2.92'''), we obtain the system

′

+− =

++− =

11 1

11 1 1

fpM

hbdp

ωα α

ααα ω



 

(23.2.93)

where

() ()

()

0000

22 2 2

00 0

2sin,4sincos,

4 sin , 2 2 sin ,

2 sin 2 sin 1

4cos 2sin 12 cos;

fmal Ipmal

bcl h m m l

dmIa l

kl m m gl

ααωα

αα

ωα α

αα α

=+ +=+

==+

=+−

⎡⎤

⎣⎦

++−++

(23.2.93')

this system of differential equations determines the oscillations of the regulator around

the motion of regime. Searching the solutions of this system in the form

11 12

e, e

λλ

αω== we obtain the characteristic equation

⎛⎞

′

+++ − =

⎜⎟

⎝⎠

hb d M

λλ λ ,

(23.2.94)

which gives the pulsations; for the damping of the oscillations, the exponential must

decreases in time, hence the real part of the roots of this equation must be negative.

According to Hurvitz’s theorem, this takes place if the conditions

⎛⎞

′

>> + −− >

⎜⎟

⎝⎠

0, 0, 0

hbbd hM

(23.2.94')

pp p

Mbd hM

ff f

⎡⎛ ⎞ ⎤

′′

−++>

⎜⎟

⎢⎥

⎣⎝ ⎠ ⎦

hold; because

> 0h , these conditions can be written in the form

Stability and Vibrations

619

⎛⎞

′′

>< +>−

⎜⎟

⎝⎠

0, 0,

bMbd hM

(23.2.94'')

The condition

> 0b asks the presence of a damping, which must satisfy the last

condition (23.2.94''). The condition

′

< 0M

is satisfied if, by an increase of the angle

α , the regulator provokes a decrease of the motive moment.

23.2.4.3 Rotor-Axletree System

Let us consider the axletree of a rotor supposed on a spherical hinge with the centre

at the point

O (Fig. 23.24). The weigh of the system rotor-axletree is P , the centre of

gravity

C being situated over the point O at the distance =OC l . The rotor is

rotating with the constant angular velocity

ω about the vertical axis of symmetry of the

discrete mechanical system. The inferior extremity of the axletree is at the distance

OM from the fixed point O . We will study the stability of the motion of rotation of

the discrete mechanical system, knowing that the moment of inertia with respect to the

axis of symmetry is

I and with respect to any other axis normal to the first one at O is

I .

Fig. 23.24 Rotor - axletree system

We consider the frame of reference

123

Ox x x with the

Ox -axis in vertical position.

The position of the axis of rotation at a given moment is specified by the position

′

of the point

M of the axis of the axletree; at a certain moment, it will coincide with the

OC -axis, while the functions of time by means of which we study the vibrations are

the co-ordinates

x and

x of the point M .

Because the elastic forces vanish at the point

′

, the differential equations of the

vibrations are of the form

21 1 2 1

22 1 1 2

Ix I x lPx

+−=

 

(23.2.95)

MECHANICAL SYSTEMS, CLASSICAL MODELS

620

multiplying the second equation by

i and introducing the complex variable

izx x, we obtain the differential equation in z

−−=

i0Iz I z lPzω  .

(23.2.95')

The characteristic equation

−−=

i0IIlPzλωλ

(23.2.96)

has the roots

()

=−

1,2 2 1 2 1

II IlPIλω ω∓

(23.2.96')

so that the solution of the differential equation (23.2.95') is

zA A

λλ

;

expressing the complex integration constants in the form

eAC

, =

eAC

where

1212

,,,CC αα

are real integration constants, the solution is written in the form

11 22

zC C

λα λα

4IIlPω

, that is if

(2/ )IIlPωω

, then the roots (23.2.96') are of

the form

1,2

iabλ ∓ , where =−>

22 1

(1/2 ) 4 0aIIlPIω , =>

/2 0bI Iω .

In this case, the general solution is given by

−+ + + +

()

tbt tbt

zC C

αα αα

(23.2.97)

One can thus deduce the equations of motion

−

=+++

11 1 2 2

21 1 2 2

e cos( ) e cos( ),

esin( ) esin( ).

xC bt C bt

αα

(23.2.97')

Observing that in the second term of the vibrations appears an increasing factor (

> 0a ),

this component has an increasing amplitude, so that the motion of rotation of the system is

instable.

4IIlPω , hence if ==

(2/ )IIlPωω , then the roots are equal, and the

general solution is of the form

=+ = +

11 2

()

12 1 2

()ee e

tbt bt

zAAt C Ct

λα α

(23.2.98)

the equations of motion being given by

Stability and Vibrations

621

=+++

11 1 2 2

21 1 2 2

cos( ) cos( ),

sin( ) sin( ).

xC bt C bt

αα

(23.2.98')

In this case too, the amplitudes of the second component are increasing, the motion of

rotation of the system being also instable.

4IIlPω > , that is if >=

(2/ )IIlPωω , then the roots =

1,2 1,2

ipλ ,

with

=−

1,2 1 1 1 2

(2/ )( 4 )pIIIIlPωω∓ , are purely imaginary. The general solution

is given by

11 22

i( ) i( )

pt pt

zC Ct

αα

(23.2.99)

while the equations of motion are written in the form

=+++

11 11 2 2 2

21 11 2 2 2

cos( ) cos( ),

sin( ) sin( ).

xC pt C pt

αα

(23.2.99')

Hence, the two natural modes of vibration are harmonic. The amplitudes of the

vibrations remain finite, so that, for >

ωω, the motion of rotation is stable. As we

have seen, the vertical position of equilibrium of the discrete mechanical system is

instable, remaining instable for

≤≤

0 ωω, but becoming stable for >

ωω.

23.2.4.4 Vibrations of Axletrees of Negligible Mass

Let be an axletree limited by two circular rigid discs, of moments of inertia

I and

I with respect to the axis of rotation; the axletree

AA is of length l , of negligible

mass and of elastic constant

klGI= where

GI is the torsional rigidity (G is the

transverse modulus of elasticity, while

is the polar moment of inertia) (Fig. 23.25).

The moments of torsion which act upon the two discs are

±−

()k θθ, where

θ and

θ are the corresponding angles of rotation.

Fig. 23.25 Axletree of negligible mass

We obtain the equations of motion

=− =−−

11 2122 21

(), ()Ik I kθθθθ θθ

 

(23.2.100)

Searching solutions of the form

11 22

e, e

λλ

θθ==, it results the algebraic system