Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

582

where

′′′

kkk,

x and

x being the displacements of the masses from the position

of equilibrium (

0xx==). When the oscillators are in the position of equilibrium,

then the mechanical system is symmetric with respect to the centre

. The reflection of

the co-ordinates with respect to the centre, followed by interchange of masses, defined

by the relation

′′

=− =−

1221

,xxxx,

(23.2.34)

lets invariant the expressions of the energies

and

; hence, the Lagrangian of the

discrete mechanical system is invariant to the transformation (23.2.34). The matrix

associated to this transformation is

−

⎡

⎤

⎢

⎥

−

⎣

⎦

(23.2.34')

From the secular equation

−DEdet[ ]μ it results

=±1μ

, hence the representation D

can be reduced to the diagonal form

⎡

⎤

⎢

⎥

−

⎣

⎦

which corresponds to the decomposition of the representation

D into two irreducible

ones. The determined symmetry does not reduce, in this case, the number of the

possible frequencies. To determine the matrix

S , we use the relation

−

⎡

⎤⎡ ⎤

⎢

⎥⎢ ⎥

−−

⎣

⎦⎣ ⎦

01 10

10 0 1

which leads to

−

⎡

⎤

⎢

⎥

⎢

⎥

⎣

⎦

11 11

21 21

Hence, the symmetry co-ordinates are given by the relations

−

⎡

⎤

⎡⎤

⎢

⎥

⎢⎥

⎣⎦

⎢⎥

⎢

⎥

⎣⎦

⎣

⎦

111112

21 1 2

()

QxSxx

Sx x

We obtain

′

−

⎡

⎤

⎡⎤

⎢

⎥

⎢⎥

′

−

⎢

⎥

⎣⎦

⎣

⎦

mkk

Stability and Vibrations

583

from (23.2.33), hence

′

⎡

⎤

⎡⎤

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

′

−

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎣⎦

⎣

⎦

SAS SBS

11 11

mkk

Because

11 21

/2SS m

, it results

′

⎡

⎤

⎢

⎥

⎢

⎥

′

−

⎢

⎥

⎣

⎦

SAS ESBS

;

the symmetry co-ordinates (23.2.35) become

() ()

112212

QxxQxx=−=+

(23.2.35)

and the frequencies of the normal mode are

′′

+−

kk kk

ωω. (23.2.35')

There result thus two modes of symmetry. One of them is

0, 0QQ≠=, where

=−

xx, the particles oscillating in the same sense; the second mode of symmetry

(

0, 0QQ=≠, where =

xx) corresponds to the case in which the particles

oscillate in opposite senses.

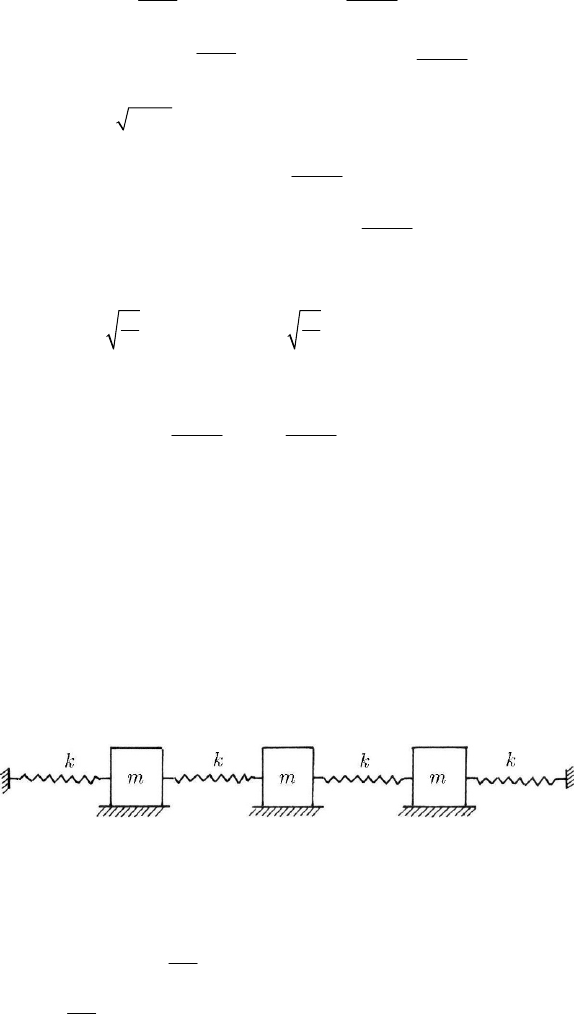
23.2.1.7 Case of Three Harmonic Oscillators

Let be now a discrete mechanical system formed of three harmonic oscillators of

equal masses

m , linked between them and at the ends by identical springs of elastic

constants

k (Fig. 23.19). We will make a direct study of this problem, in which – for

the sake of simplicity – we have chosen, as mentioned above, equal elastic constants.

Fig. 23.19 Problem of three harmonic oscillators of equal masses

The displacements of the masses from the position of equilibrium are

, xx and

x , so that we can write

()

()()

=++

=+−+−+

⎡⎤

⎣⎦

222

123

121 32 3

T xxx

Vkxxxxxx



(23.2.36)

MECHANICAL SYSTEMS, CLASSICAL MODELS

584

We obtain Lagrange’s equations

()

+−=

−−+=

−−=

112

2123

323

20,

xpxx

xpx xx

xpx x



(23.2.37)

where we have introduced the notation

/pkm. The characteristic equation is

22 2

det 2 0

pp p

⎡⎤

−−

⎢⎥

−−−=

⎢⎥

−−

⎣⎦

(23.2.37')

which leads to the roots

2 2 0.766 ,

21.414,

221.848;

ωλ

==−=

===

==+=

(23.2.38)

there correspond the proper modes

11 1121 11

31 1 1

12 222 32 22

13 332 3 33

33 3 3

cos( ), 2 cos( ),

cos( ),

cos( ), 0, cos( ),

cos( ), 2 cos( ),

cos( ).

xa t xa t

xa t

xa t x xa t

xa t x a t

xa t

ωϕ ωϕ

ωϕ

ωϕ ωϕ

ωϕ

=−= −

=−

=− − = = −

=−=− −

=−

(23.2.39)

Using the results in Sect. 23.2.1.4, one can easily verify the orthogonality of these

proper modes.

By superposition, we obtain the general solution

=−−−+−

=−− −

=−+−+−

11 1 1 2 2 2 3 3 3

21 1 1 3 3 3

31 1 1 2 2 2 3 3 3

cos( ) cos( ) cos( ),

2 os( ) 2 cos( ),

cos( ) cos( ) cos( ).

xa t a t a t

xa t a t

xa t a t a t

ωϕ ωϕ ωϕ

ωϕ ωϕ

ωϕ ωϕ ωϕ

(23.2.39')

Denoting

′

=−

′

=−

′

=−

11 1 1

22 2 2

33 3 3

cos( ),

xa t

ωϕ

(23.2.39'')

Stability and Vibrations

585

we get the linear transformation

()

1123

212

3123

xxxx

xxx

xxxx

′′′

=−+

′′

=−

′′′

=++

(23.2.39''')

The expressions (23.2.36) take the form

()

() ()

′′′

=++

′′ ′

=− +++

⎡⎤

⎣⎦

222

123

22 2

12 3

22 2 2 2 .

Tmxxx

Vk xx x



(23.2.36')

Lagrange’s system of equations becomes

()

′′

+− =

′′

++ =

22 0,

20,

22 0,

xpx



(23.2.37'')

being an uncoupled system; obviously, we find again the proper pulsations (23.2.38).

23.2.1.8 Small Oscillations with One Degree of Freedom

In the case of a discrete mechanical system with only one degree of freedom

(

= 1s ), corresponding to the generalized co-ordinate q , we have

== >

,,,0

TaqVbqab



;

(23.2.40)

we obtain the equation of motion

+= =

ωω ,

(23.2.41)

with the general solution

=−=− −>() cos( ), () sin( ), 0qt A t qt A t Aωϕ ω ωϕ ,

(23.2.41')

where the integration constants can be determined by the initial conditions

(0) , (0)qqqq== in the form

=+ =

,tan



(23.2.41'')

Obviously, the motion is given by a harmonic oscillation of pulsation

ω , which does

not depend on the initial conditions.

MECHANICAL SYSTEMS, CLASSICAL MODELS

586

Eliminating the time

t between the relations (23.2.41'), we obtain a family of

ellipses

()

Aω



(23.2.41''')

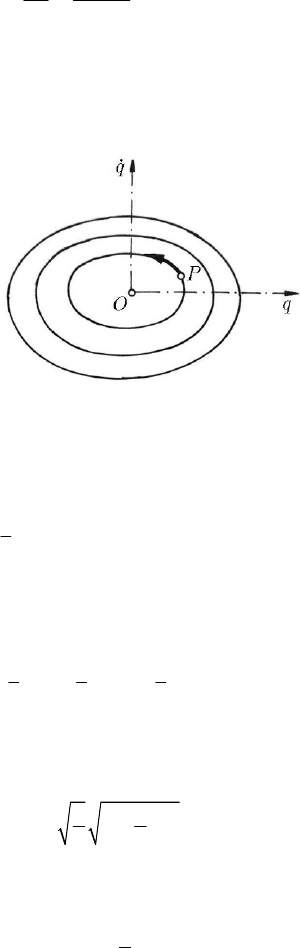
in the phase plane (Fig. 23.20); these ellipses are concentric, of semi-axes

A and Aω ,

and are obtained from one of them by a dilatation of modulus

A . The representative

point

(,)Pqq describes counterclockwise the corresponding ellipse.

Fig. 23.20 Small oscillations with one degree of freedom

We supposed in (23.2.40) that

≠

d/d 0Vq ; to make vanish this derivative, we

choose

=∈>>

,,1,0

Vbqn nb` ,

(23.2.42)

so that the position

= 0q does correspond to a minimum of the potential energy. The

theorem of conservation of the mechanical energy leads to

11 1

22 2

aq bq h ,

(23.2.43)

where

h is the energy constant, which may be determined by initial conditions. Hence,

we can write

=± −



(23.2.43')

wherefrom it results

()

−<< = >

1/2

111 1

,,0

qqqq q

;

(23.2.43'')

Stability and Vibrations

587

the discrete mechanical system will oscillate between the positions which are symmetric

with respect to the stable position of equilibrium

= 0q , with the period

⎛⎞

−

⎜⎟

⎝⎠

∫

(23.2.43''')

We mention that these oscillations are harmonic only in the particular case

= 1n

previously considered.

23.2.1.9 Small Oscillations with Two Degrees of Freedom

In the case of a discrete mechanical system with two degrees of freedom (

= 2s ), we

have

()

11 1 12 1 2 22 2

Taqaqqaq

Vbqbqqbq

=++



(23.2.44)

We assume that

≠

0b , otherwise the form V is no more positive definite; in this

case, we can make the substitution

=− =

11 233

qq qqq

following to which the term

qq disappears from the expression of the potential

energy. We can thus consider

0b in the expression of this energy. One obtains

thus Lagrange’s equations

++=

11 1 12 2 11 1

12 1 22 2 22 2

aq aq bq

 

We pass to normal co-ordinates by relations of the form

′′ ′′

=+ =+

11111222211222

,qqqqqqαα αα,

(23.2.45)

where

=,, 1,2

ijα , are real constants, which can be determined so as to obtain

()()

′′ ′′

=+ = +

22 222

12 112

TqqV qq

ω ;

(23.2.44')

replacing (23.2.45) in (23.2.44) and identifying, we get the relations

MECHANICAL SYSTEMS, CLASSICAL MODELS

588

++=

+++=

11 11 12 11 21 22 21

11 12 12 12 22 22 22

11 11 12 12 11 22 12 21 22 21 22

21,

()0,

aa a

αααα

αα αα αα αα

(23.2.45')

11 11 12 22 21 22

222

11 11 22 21 1

222

11 12 22 22 2

αα αα

ααω

(23.2.45'')

The last two relations (23.2.45') lead to

()

−

+=−

=−

11 22 22 11

11 22 12 21 11 12

12 22

11 22 12 21 11 12

ab ab

αα αα αα

αααα αα

We can thus express the unknowns of the transformation (23.2.45) in the form

21 1 11 22 2 12

, kkαααα==, where

k and

k are the roots of the equation of second

degree

()

+− −=

12 22 11 22 22 11 12 11

0abk ab ab k ab ,

(23.2.46)

that is

()

⎡⎤

=− − ± − +

⎣⎦

1,2 1122 2211 1122 2211 121112

12 22

k abab abab abb

(23.2.46')

We notice that

11 22

,0bb , the form V being positive definite; hence, the discriminant

of the equation is positive, the roots

k and

k being thus real. The two roots are of

different sign, let be – for instance –

0, 0kk<>. Replacing in the first two

relations (23.2.45'), we obtain

++ ++

11 12

22 1 12 1 11 22 2 12 2 11

22ak ak a ak ak a

αα

The kinetic energy being positive definite, we can state that

11 12

,αα are real quantities;

in this case, we can calculate also

21 22

,αα , which will be real quantities too.

The relation (23.2.45'') will give, finally, the pulsations, in the form

22 1 11 22 2 11

22 1 12 1 11 22 2 12 2 11

bk b bk b

ak ak a ak ak a

ωω

++ ++

;

(23.2.46'')

these quantities are real too, because the potential energy is positive definite. We are

thus led to the normal co-ordinates

Stability and Vibrations

589

′

=−=cos( ), 1,2

ii i i

qa t iωϕ ,

the amplitudes

,aa and the phase shifts

,ϕϕ being determined by the initial

conditions. Taking into account (23.2.46), (23.2.46'), we can calculate

()

−= − +

⎡

⎤

⎣

⎦

3/2

22 2

1 2 11 22 22 11 12 11 12

12 22

4ab ab abb

ab P

ωω

where we have denoted

()()

=++ ++

22 1 12 1 11 22 2 12 2 11

22Pak akaak aka

Obviously, this difference is positive, so that we can state

ωω; this result

corresponds to the signs chosen for

and

The generalized co-ordinates (23.2.45) will thus be given by

=−+−

11111112222

22111122222

() cos( ) cos( ),

qt a t a t

αωϕαωϕ

being a linear combination of the normal co-ordinates. We can assume that

11 12

,0αα ; in this case

0α < and >

0α . We can also write

=+ −

=− + −

1111122

22111222

() cos cos( ),

qt A t A t

qt Aa t A t

ωωϕ

(23.2.47)

where

=,, 1,2

Aij

, are amplitudes (positive quantities) and where we have

conveniently changed the origin of the time, so that to appear a phase shift only in the

second normal co-ordinate.

If the two vibrations have the same direction, then one can make a study analogue to

that in Sect. 8.2.2.4 for the interference phenomena, the beats etc.

23.2.1.10 Methods to Determinate the Proper Pulsations

If the number of degrees of freedom of a discrete mechanical system is great, then

can appear difficulties in solving the secular equation; in this case, it is convenient to

use some approximate methods of calculation.

In the case of a discrete mechanical system, we start from the matric equation

(23.2.18), written in the form

−=KC MC

ω 0 .

(23.2.48)

Multiplying at the left by the transpose matrix

to obtain a scalar, it results

CKC

CMC

ω ;

(23.2.49)

MECHANICAL SYSTEMS, CLASSICAL MODELS

590

we can also write

∑∑

ij i j

kCC

mCC

(23.2.49')

In the case of statically coupled discrete mechanical systems (

mij=≠), we

obtain

∑∑

∑

ij i j

ii i

kCC

(23.2.49'')

These formulae are exact; but we must know the proper forms of vibrations, hence the

coefficients

, 1,2,...,

Ci n= .

In Rayleigh’s method one introduces the generalized forces

∑

, 1,2,...,

iijj

Fkxi n;

replacing these forces by

m and the displacements

x by the coefficients

C , it

results

, 1,2,...,

ii ij j

mkCi n

∑

Multiplying by

C and summing, we can write

===

∑∑∑

111

nnn

ii i ij i j

iij

mC kCC .

Finally, we get the approximate formula

∑

ii i

ω ,

(23.2.49''')

where

C are the displacements produced by the generalized forces

F , numerically

equal to

m .

Stability and Vibrations

591

Let us return to the case of three harmonic oscillators, considered in Sect. 23.2.1.7;

we have

11 22 33

, 0,

mmmmm ij=== =≠, ===

11 22 33

2kkk k,

12 21

kk=

kk==−, ==

13 31

0kk . The coefficients , 1,2,3

Ci= , will be given by

the system

−=−+ −=−+ =

12 1 23 2 3

222kC kC kC kC kC kC kC m

;

it results

13 2

3/2, 2/CC mkC mk== = . The formula (23.2.49''') leads to

0,767

ω ;

comparing with the minimal pulsation corresponding to the fundamental proper form

given by (23.2.38), we have an error of 1.31‰, hence a very good approximation.

≠Kdet 0 , then we can calculate

−

, and (23.2.48) leads to

−

==CCKM

,ωα α ;

(23.2.48')

we have always

≠Mdet 0 , so that

−

does exist and we can obtain analogously

−

==CC MK

,ωββ .

(23.2.48'')

Starting from (23.2.48) or from (23.2.48'), we can use a method of matric iteration. We

consider a column matrix

for the proper form; one of the mentioned formulae

allows us to calculate a matrix

a.s.o., till an approximation of order n , when the

forms

and

−

are in direct proportion, with a good approximation. The formula

(23.2.48') leads to the fundamental proper form, corresponding to the smallest proper

pulsation, while the formula (23.2.48'') allows to calculate the fundamental proper form,

corresponding to the greatest proper pulsation. One can thus appreciate the spectrum of

the proper pulsations.

In the previously considered problem, we have

⎡

⎤

⎡⎤

−

⎢

⎥

⎢⎥

==−−

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

−

⎢⎥

⎢

⎥

⎣⎦

⎣

⎦

00, 2

mkkk

so that

3/4 1/2 1/4

210

1/2 1 1/2 , 1 2 1

012

1/4 1/2 3/4

⎡⎤

⎡

⎤

−

⎢⎥

⎢

⎥

==−−

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

−

⎢⎥

⎢

⎥

⎣

⎦

⎣⎦

αβ