Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

572

, const, 1,2,...,

jj j

cc j s== =0a

;

is this case

(, ) (, )

jj j

cc=Aa a Aa a ,

for any fixed

, 0kks<<. But

0, ,

(, )

0, ,

≠

⎧

⎪

⎨

⎪

⎩

Aa a

so that

0, 1,2,...,

cj s== ; we can thus state that the amplitude vectors are linear

independent.

We impose Cauchy type initial conditions

(0) cos ,

(0) sin .

jj j

jjj j

ωϕ

∑



qaq

(23.2.13)

The vectors

being linear independent, we determine uniquely cos

C ϕ and

sin

C ωϕ; because 0

ω ≠ , we obtain then the arbitrary constants

C and

ϕ (for

the latter constants, till a multiple of

2π ).

Hence, in the absence of multiple roots of the secular equation, the formula

(23.2.12') gives the general solution of the system of equations of motion (23.2.4').

Lagrange considered, erroneously, that in case of multiple roots appear solutions of

the form

()

... costt tωϕ

′′′

++ + −aa a

;

but Weierstrass showed further that to each root

λ of m th order of multiplicity one

can determine

m linearly independent amplitude vectors

a , the final solution being of

the same form (23.2.12').

The vibrations

cos( ), 1,2,...,

jj j j

Cjsωϕ−=a , are also called principal

vibrations of the discrete mechanical system.

23.2.1.3 Vibrations of a Discrete Mechanical System

In particular, we can assume that the system of equations of motion (23.2.4)

or (23.2.4') corresponds to a discrete mechanical system of particles. If this system has

only one degree of freedom, specified by the variable

x , we can write

(1/2)Tmx= 

and

(1/2)Vkx= , where m is a mass, while k is a coefficient of elasticity.

In the case in which the mechanical system has

n degrees of freedom, by

generalizing, we can write

Stability and Vibrations

573

11 11

nn nn

ij i j ij i j

ij ij

T m xx V k xx

== ==

∑∑ ∑∑

 ,

(23.2.14)

where the variables

, 1,2,...,

xi n= , correspond to the degrees of freedom,

ij ji

mm=

are quantities of the nature of a mass, while

, , 1,2,...,

ij ji

kkij n== , are quantities

of the nature of a coefficient of elasticity. Introducing the matrix of inertia (the matrix

of masses) and the matrix of rigidity (the matrix of elastic coefficients)

11 12 1

21 22 2

...

... ... ... ...

...

kk k

mm m

kk k

mm m

kk k

==MK

(23.2.15)

as well as the column vectors

⎡

⎤

⎡⎤

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎢

⎥

⎢⎥

⎣⎦

⎣

⎦



(23.2.15')

we can write

TV==



xMx xKx

(23.2.14')

Lagrange’s equations taking the form

+=0



Mx Kx . (23.2.16)

The coefficients

ij ji

mmij=≠, if they are not null, are called coefficients of

dynamical coupling and the coefficients

ij ji

kkij=≠, if they are not zero, are

called coefficients of statically coupling. If

mij=≠, and if there exist

coefficients

kij≠≠, then the mechanical system is statically coupled. If

kij=≠ existing coefficients 0,

mij≠≠, then the mechanical system is

dynamically coupled. If

ij ij

mk ij== ≠ then the mechanical system is

uncoupled, each differential equation (23.2.16) having only one degree of freedom

(only one unknown function)

+==0, 1,2,...,

ii i ii i

mx kx i n ,

(23.2.16')

unlike the system (23.2.4). We assumed that

=, 1,2,...,ij n, in all the above

considerations.

MECHANICAL SYSTEMS, CLASSICAL MODELS

574

Starting from the solution

()

=−xCcos tωϕ

(23.2.17)

and using the results in the preceding subsection, one can state that the general solution

is obtained as a superposition of

n proper modes, depending on 2n constants of

integration, which are expressed by means of the initial positions

(0)

and of the

initial velocities

(0) , 1,2,...,

xxi n== , in a Cauchy type problem. The column

vector

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

(23.2.15'')

is given by the linear and homogeneous matric equation

ω−=

⎡⎤

⎣⎦

0KMC,

(23.2.18)

which leads to the characteristic equation

−=

⎡⎤

⎣⎦

det 0ω ;

(23.2.18')

to each eigenvalue

, 1,2,...,

inω = , will correspond a proper form of vibration C

of components

, ,..., , 1,2,...,

ii i

CC C i n= , having – in total – n such forms.

23.2.1.4 Proper Forms of Vibration

Let be two proper forms of vibration, denoted by “prime” and “second”. By writing

the equation (23.2.18) for the two cases, it results

;

′′ ′

−=

′′ ′′ ′′

−=

KC MC

multiplying the first equation at the left by

′′

and the second one by

′

, we obtain

T2T

′′ ′ ′ ′′ ′

−=

′′′′′′ ′′

−=

CKC CMC

The matrices

K and M are symmetric with respect to the principal diagonal; it results

that the scalars

′′ ′

CKC

and

′′ ′

CMC

are symmetric with respect to

,, , 1,2,...,

CC ij n

′′

= , so that we can replace

′

C by

′′

C and

′′

C by

′

C . It results

′′′′′′′′ ′′ ′′

CKC CKCCMC CMC

TTT T

, .

Stability and Vibrations

575

We can thus write

()

22T

ωω

′′′′′′

−=

0CMC ;

but

′′ ′

≠

ωω, so that, finally

′′ ′

0CMC .

(23.2.19)

Analogously,

′′ ′

0CKC ,

(23.2.19')

obtaining thus the property of orthogonality of the proper modes. Developing these

relations, we get

== ==

′′′ ′′′

∑∑ ∑∑

11 11

0, 0

nn nn

ijij ijij

ij ij

mCC kCC .

(23.2.20)

If the mechanical system is statically coupled, then it results

===

′′′ ′′′

∑∑∑

111

0, 0

nnn

ii i i ij i j

iij

mCC kCC ,

(23.2.20')

while, if the system is dynamically coupled, we can write

== =

′′′ ′′′

∑∑ ∑

11 1

0, 0

nn n

ij i j ii i i

ij i

mCC kCC ;

(23.2.20'')

finally, if the discrete mechanical system is uncoupled, we have

′′′ ′′′

∑∑

0, 0

ii i i ii i i

mCC kCC .

(23.2.20''')

Let be

()

′′ ′ ′

−= −=

∑∑

cos , 1,2,...,

ij j ij j

mx mC t i nωωϕ ,

the forces of inertia corresponding to the “prime” mode, where we took into account the

displacements

cos( ), 1,2,...,

xC t j nωϕ

′′ ′′

=−=

; if we consider also the

displacements

cos( ), 1,2,...,

xC t j nωϕ

′′ ′′ ′′ ′′

=−=

, corresponding to the “second”

mode, and if we calculate the work of the mentioned forces of inertia, when they travel

through these displacements, with all their intensity, then we obtain

MECHANICAL SYSTEMS, CLASSICAL MODELS

576

()( )

′′′ ′ ′ ′′ ′′

=−−

∑∑

cos cos

ij i j

WmCCt tωϕ ω ϕ.

The orthogonality condition (23.2.20) (or, in particular, the condition (23.2.20'')) leads

= 0W

; (23.2.21)

we can thus state

Theorem 23.2.1 In the case of a discrete mechanical system of particles, the work of

the forces of inertia corresponding to a proper mode of vibration vanishes if they travel

through, with all their intensity, the displacements corresponding to another mode.

Observing that this work is equal to the variation of the kinetic energy, we can also

state

Theorem 23.2.1' In the case of a discrete mechanical system of particles there does not

take place a transfer of energy from a proper mode of vibration to another one.

23.2.1.5 Normal Co-ordinates

We state, without proof,

Theorem 23.2.2 (J. J. Sylvester). If A and B are two real and symmetric matrices

and if

A is positive definite, then it exists a non-singular real matrix S , so that

==SAS ESBS

, Λ

(23.2.22)

where

E is the unit matrix and Λ is a diagonal matrix

0...0

... ... ... ...

00...

(23.2.22')

the non-zero elements (the eigenvalues) of which are the roots of the equation

[

]

−=BAdet 0λ .

(23.2.22'')

We notice that

[]

()

[]

()

[]

det det det det det

det det det det det ,

λλ λ

λλ

−= − = −

⎡⎤

⎣⎦

=−=−

ES ASS AS

SS A S A

ΛΒ Β

ΒΒ

where

det ≠ 0S , the matrix S being non-singular; hence −Bdet[ ]λΛ vanishes

together with

− Edet[ ]λΛ .

Stability and Vibrations

577

The change of co-ordinates

1−

′

qSq

(23.2.23)

transforms the equation (23.2.4') in the form

′′

qq0



Λ ,

(23.2.24)

to which – taking into account the above observation – corresponds a secular equation

with the same roots. We can thus state that Lagrange’s equations are invariant to the

point transformation (23.2.23), defined by the matrix

S , the form (23.2.24) being the

normal form, while the co-ordinates

′

q are normal co-ordinates. We mention that the

matrices

A and B are simultaneously diagonal if all the co-ordinates are normal,

hence if between the equations of motion there is not any coupling.

The solution of the system of equations (23.2.24) will be thus independent, of the

form

′′

=−=

qa( ) cos( ), 1,2,...,

jjjj

ttjsωϕ ,

(23.2.24')

Any independent normal co-ordinate

′

of (23.2.24') depends on the eigenvalues

λ , hence on the pulsation =

ωλ, on the proper form

′

and on the arbitrary

phase shift

ϕ ; by means of the arbitrary constants

′

C , we obtain the general solution

()

′′

=−

∑

() cos

jjj

tC tωϕ,

(23.2.24'')

corresponding to the solution (23.1.12'). We notice that this solution is general, even if

the characteristic equation has multiple roots.

We can thus state

Theorem 23.2.2 (Daniel Bernoulli). The permanent small motions of a discrete

mechanical system, subjected to holonomic and scleronomic constraints and to

conservative forces around a stable position of equilibrium can be obtained by the

superposition of a finite number of independent harmonic vibrations.

The kinetic energy and the potential energy can be expressed in normal co-ordinates

in the form

′′

∑∑

222

TqV qω .

(23.2.3''')

There are two principal problems in the theory of oscillations: the determination of

the possible frequencies of the normal modes and the determination of the normal

co-ordinates as functions of the co-ordinates in which the problem has been initially

formulated. The frequencies are given by the secular equation (23.2.8'), while it is more

MECHANICAL SYSTEMS, CLASSICAL MODELS

578

difficult to obtain the normal co-ordinates, because one must determine the matrix

for the transformation (23.2.22). As a matter of fact, by the determination of the matrix

S one obtains also the frequencies of the normal modes directly from the relation

= SBS

Λ . In both problems, one must know all the masses of the particles, as well as

the constants which characterize the forces, that is the matrices

and

. From

symmetry considerations, we have the possibility to determine the limits of the number

of possible frequencies, the superior limit of the number of constants necessary to

specify

T and V , a partial factorization of the secular equation and the co-ordinates in

which the matrices

A and B are expressed in a reduced form (not necessary diagonal).

Let us suppose that one can find a matrix

≠DE

, of the same dimension as the

vector

q , so that

()

=∀Dq q q(),VV;

(23.2.25)

in this case, the configurations

q and Dq have the same potential energy. Because

()()() ()

===Dq Dq B Dq q D BDq q

22VV

it results that

=DBD B

(23.2.26)

At the same time, the relations

()

() () ()

===Dq D Dq Dq q

()VV VV

take place and, replacing

q by

−

in (23.2.25), we get

()

()VV

−

=Dq q

, so that

the group

G generated by D lets invariant the potential V . The set of matrices D

which satisfy the relation (23.2.25) forms a representation of the group

G .

Let us suppose that the relation

=DAD A

is satisfied too, hence that the

Lagrangian (23.2.3''') is invariant with respect to the transformations of the group

G . If

the representation

D is orthogonal and completely reducible, having each irreducible

component orthogonal, then the equation (23.2.26) becomes

=BD DB , (23.2.26')

where

()()

(1)

(2) ( ) ( ) T 1

−

⎡⎤

⎢⎥

===

⎢⎥

⎣⎦

DDDDDD

(23.2.27)

Stability and Vibrations

579

Be a permutation of the rows of the matrix

D (which is equivalent to a transformation

of similitude), we may group all the equivalent irreducible elements of the reduced form

(23.2.27) in the form

⎡⎤

⎢⎥

⎣⎦

(1)

(2)

(23.2.27')

It results, from the relation (23.2.26'), that the matrix

commutes with the matrices of

the representation

D and, according to Schur’s lemma, must be of the form

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

(1)

(2)

(23.2.28)

where

()k

is a submatrix of the same dimension as the block of all the matrices

()k

form (23.2.27'); as well, the matrix B

()k

must be given by

()

() ()

11 12

() ()

() () ()

21 22

() ()

...

... ,

... ... ...

, , 1,2,..., ,

kk k

ij ji

ij s

ββ

⎡⎤

⎢⎥

== =×

⎢⎥

⎣⎦

BB EE Eβ

(23.2.28')

where we have put in evidence the Cartesian product of the matrix

()k

by the unit

matrix and where

()

() () () ()

dim , dim ,

kk k k

nc== =E

βββ

, while

()k

c shows

how many times is

()k

contained in D . As well,

⎡⎤

⎢⎥

==×

⎢⎥

⎣⎦

AAA E

(1)

(2) ( ) ( )

(23.2.28'')

()k

α being a matrix; we obtain thus the secular equation

MECHANICAL SYSTEMS, CLASSICAL MODELS

580

[]

()

() ()

det det 0

λλ

⎡⎤

−= − =

⎣⎦

∏

BA βα

(23.2.28''')

Hence, the number of the different frequencies is at the most equal to the number of the

irreducible components of the representation

D and the degeneration of each

frequency is at least equal to the dimension of the corresponding irreducible

component. Because the representation

D can be reduced by a real transformation, we

can assume that the transformed matrix

is real. Thus, the number of the real

constants necessary to can determine the matrices

and

is given by

()

∑

() ()

cc ,

(23.2.29)

corresponding to the decomposition in a direct sum

⊕

∑

() ()ii

cDD.

(23.2.29')

If an irreducible component

∈

()k

appears only once in (23.2.29'), then

()k

and

()k

are diagonal matrices, while the corresponding symmetry co-ordinates (in which

the representation

D is completely reduced) are normal co-ordinates.

Let be two systems of normal co-ordinates

′

and

′′

. Let us suppose that, in the

normal co-ordinates

′

, the matrices A and B have the form

⎡

⎤

⎢

⎥

===

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

AEB A

Λ ,

(23.2.30)

where each matrix

is a scalar matrix (which has only one element), with

ij≠≠ΛΛ . If

1−

′′ ′

qRq

, then, in these co-ordinates, the matrices A and B

will be of the form

′

ARAR

and

′

BRR

Λ ; because the co-ordinates

′′

are

normal, so as to have

′

=AE

and

′

=B Λ

, the matrix R must satisfy the relations

==RR ER R

, ΛΛ,

(23.2.31)

that is

[,]=−=0RRRΛΛΛ . It results that the most general form of the matrix R ,

which transforms a system of normal co-ordinates in another system of co-ordinates,

normal too, maintaining the order of eigenvalues in the matrix

Λ , is

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

(23.2.31')

Stability and Vibrations

581

If the representation

D given by (23.2.29') is real, before taking the reduced form,

then we can suppose that it took this form by a real transformation, so that the matrices

()k

α and

()

of the relations (23.2.28'), (23.2.28'') must be real. Because these

matrices are symmetric, while

()k

α is positive definite, there exists a non-singular real

matrix

, so that =SSE

T() ()kk

α and

T() () ()

kkk

=SSbbβ being a diagonal

matrix. Hence,

()()

××=×

SE A SE EE

SE B SE bE

()

kk kk kk

(23.2.32)

if the rows of the Kronecker products are correspondingly ordered. We notice that the

system of co-ordinates

−

=QSq

is a system of normal co-ordinates for

⊕

=×

∑

SSE,

(23.2.32')

while

−

=SDS D

. In normal co-ordinates Q , the representation D is completely

reduced to irreducible components. The matrix (23.2.31') transforms each irreducible

component of

D is an equivalent irreducible component. Hence, all the systems of

normal co-ordinates for which

Λ is of the form (23.2.30) are systems of symmetry

co-ordinates.

The normal co-ordinates which correspond to different frequencies cannot be

transformed one into another because, if

Q is a normal co-ordinate, obtained by a

transformation, then

jjj

QQω



, and if

′

Q is also a normal co-ordinate, obtained

by a transformation, then

′′

jjj

QQω



and it is impossible to appear, in the

expression of

′

Q , other frequencies than /2

f ωπ= .

23.2.1.6 Case of Two Harmonic Oscillators

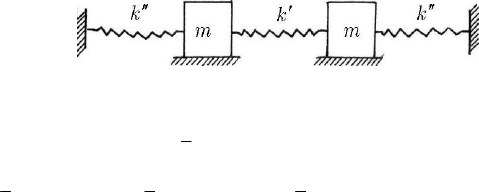
Let us consider a discrete mechanical system formed of two harmonic oscillators of

equal masses

m , linked at the ends by identical springs of elastic constants

′′

k , the

spring between them being of elastic constant

′

k (Fig. 23.18). The kinetic energy and

the potential energy of this system are

Fig. 23.18 Problem of two harmonic oscillators of equal masses

()

22 22

12 12 12 12

11 1

22 2

Tmxx

Vkxx kxx kxxkxx

′′ ′ ′

=++−=+−



(23.2.33)