Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

552

To fix the ideas, we consider the particular system

()

=− + − −

=+−−

222

2121

222

1122

xRxxx

(23.1.77)

to which corresponds as a limit cycle the circle

22 2

xxR. Passing to polar

co-ordinates (

cos , sinxr xrθθ==

), we obtain

()

cos sin sin cos ,

sin cos cos sin ;

rr r Rrr

θθθ ω θ θ

θθθω θ θ

−=−+−

−= +−



(23.1.77')

hence, it results

()

=− =

,rRrrθω



(23.1.77'')

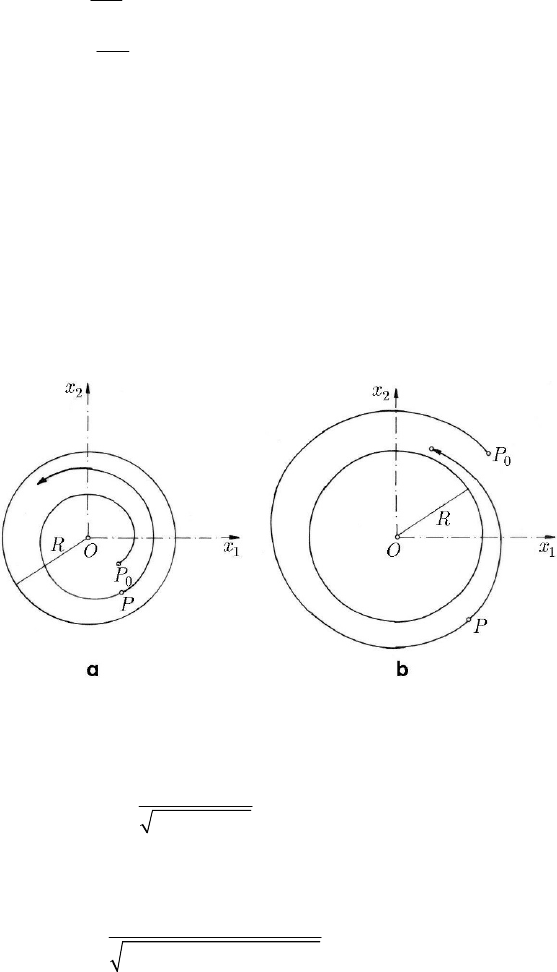
Fig. 23.14 Stable limit circles: (a)

rR< ; (b)

rR>

Integrating, we can write

−

==+

rtB

θω

;

(23.1.78)

the initial conditions

(0) , 0, (0) 0rrr θ=≠ = lead to

()

−

+−

22 2

1/1e

θω

;

(23.1.78')

We also notice that

Stability and Vibrations

553

→∞

=lim

rR;

(23.1.78'')

both for

(Fig. 23.14a) and for

(Fig. 23.14b); the circle =rR

represents, in this case, a stable limit cycle. In particular, if

rR, then the motion

takes place only on the circle. The origin corresponds to a case of instability.

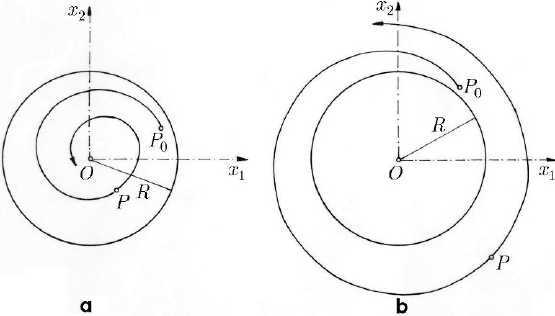
There exist also systems of differential equations for which the limit cycle is instable,

the trajectory moving away from it; in this case, the origin can be a stable position “in

small” (Fig. 23.15a) or an instable position “in great” (Fig. 23.15b). We mention also

the possibility that the limit cycle be semi-stable, so that to have the situation in

Figs. 23.14b and 23.15a or the situation in Figs. 23.14a and 23.15b.

Fig. 23.15 Instable limit cycle around: (a) a stable position “in small”;

(b) an instable position “in great”

In general, the limit cycles which are encountered in practice have the property that

to each of them comes close not only one trajectory in spiral, but an infinity of such

trajectories, which pass through the ordinary points of the phase plane and which fill in

at least a domain which contains the cycle

C . If one takes into account that any

ordinary point

of the phase plane can be considered to be a given initial position and

that the motion on the limit cycle does not depend on the initial conditions, in the sense

that all the trajectories which pass through various points of the phase plane tend to a

same limit cycle.

The important distinction between the closed trajectories of conservative mechanical

systems and the closed trajectories of limit cycle type consists in the fact that the first

ones appear always in the form of a continuous family of curves, while the other ones

appear – in general – in the form of isolated curves. In conclusion, if

C is a closed

trajectory of limit cycle type, then do not exist other closed curves which be trajectories

and differ arbitrarily little of

C .

This can be easily seen by comparing a conservative mechanical system (e.g. a

mathematical pendulum for which the motion is completely definite by means of the

MECHANICAL SYSTEMS, CLASSICAL MODELS

554

prescribed initial conditions) to a mechanical system with a limit cycle (e.g., a watch for

which the motion of regime does not depend on the initial conditions).

In general, the problem of putting in evidence the limit cycles is very difficult. We

mention, in this direction, the theory of indices, initiated by H. Poincaré in 1892 in his

treatise about new methods in celestial mechanics (Poincaré, H., 1892–1899) and

developed by I. Bendixon in 1901. We state thus

Theorem 23.1.22 (Bendixon). If

11 22

(), (), xxtxxttt==>, is the parametric

representation of the trajectory

′

and if, for →∞t , the curve

remains in the

interior of a bounded domain D , without coming close to a singular point, then

′

constitutes either a closed trajectory

C or tends to such a trajectory in D .

This theorem gives a necessary and sufficient condition of existence of a closed

trajectory.

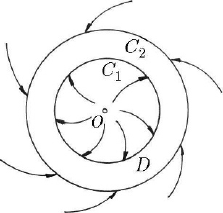
Fig. 23.16 Graphical representation of the Bendixon theorem in a two-dimensional space

Let us return to the preceding example. Obviously, for

r sufficiently great the

trajectories are directed towards the interior. Using the substitution

111

xxξ=+,

222

xxξ=+, the equations are brought to the form

=− + =− ++

11 2 2 12

..., ...ξξωξ ξ ωξξ



(23.1.77''')

where we have neglected powers of higher order. The origin of the co-ordinates

represents an instable focus, so that the trajectories start from the origin and enter in the

domain

D through the internal frontier

C (Fig. 23.16). As well, the trajectories enter

in the domain

D from the exterior through the external frontier

C . We notice also

that the domain

D does not contain singular points; hence, in the interior of this

domain there exists a stable limit cycle.

But it is not always possible to define such a domain

D , so that this theorem can no

more be used in this case.

23.1.3 Applications

In what follows, we present some applications to the motion of the rigid solid,

especially to the motion of rotation about the principal axes of inertia; as well, we

consider the motion of a projectile in rotation. We mention also the motion in a central

field.

Stability and Vibrations

555

23.1.3.1 Motion of Rotation of the Rigid Solid

We consider firstly the motion of a rigid solid with a fixed point

, subjected to the

action of its own weight

=GgM , applied at the centre of mass C , in the hypothesis

≡CO (see Sect. 15.1.1.6). The equations of motion (15.1.40) can be written in the

form

()

11 2 3 23

22 3 1 31

33 1 2 12

III

ωωω

=−



(23.1.79)

with respect to the axes of the non-inertial frame of reference, rigidly connected to the

rigid solid, which are principal axes of inertia; Euler’s equations (15.1.11'') have the

same form if we equate to zero the moment

of the external forces

(

123

OOO

MMM===). One makes a direct study of the permanent rotations in

Sect. 15.1.2.7. We assume that the principal moments of inertia are ordered in the form

123

III. The unknown functions are the components of the rotation vector ω .

We are in the Euler–Poinsot case of integrability.

Let us consider a rotation about the axis

Ox ; a unperturbed motion is characterized

=== =

123

0, 0, , constωωωωω ,

(23.1.80)

which – obviously – verifies the system of equations (23.1.79). Let be the perturbed

motion

===+

11223 3

,,ωεωεωωε,

(23.1.80')

where

123

,,εεε are arbitrarily small angular velocities, functions of time. Replacing in

(23.1.79), we obtain

()

=− +

=−

11 2 3 3 2

22 3 1 3 1

33 1 2 12

III

εωεε

εεε



(23.1.79')

Linearizing, we can write

()

=−

11 2 3 2

22 3 1 1

III

εωε



(23.1.79'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

556

The characteristic equation (of the form (23.1.34))

−

−=

−

λω

ωλ

leads to

()()

()

⎡⎤

−− − =

⎣⎦

12 2 3 3 1 3

0II I I I Iλλ ω ;

(23.1.81)

one of the roots vanishes, while the other ones are given by

()()

−−

=± >

2331

1,2 3 3

IIII

λωω

(23.1.81')

Assuming for the principal moments of inertia the order mentioned above, there

result two imaginary roots; hence, the motion of rotation about the axis of minimal

principal moment of inertia is simply stable.

In case of a rotation about the axis

Ox , we proceed analogously and find the purely

imaginary roots of the characteristic equation in the form (excepting the zero root)

()()

−−

=± >

3112

1,2 1 1

IIII

λωω

;

(23.1.81'')

hence, the motion of rotation about the axis of maximal principal moment of inertia is,

as well, simply stable. Let be now a rotation about the axis

Ox ; after an analogous

study, excepting the zero root, one obtains the real roots

()()

−−

=± >

1223

1,2 2 2

IIII

λωω

(23.1.81''')

one of them being positive, so that we can state that the motion of rotation about the

axis of mean principal moment of inertia is instable.

We find thus again the results in Sect. 15.1.2.7 for permanent rotations.

In the case of the system (23.1.79'), we multiply the first equation by

−

311

()IIε

and the second equation by

−

232

()IIε and subtract the equations thus obtained one of

the other; it results

() ()

−−− =

13 111 22 322

0II I II Iεε εε



Stability and Vibrations

557

wherefrom we obtain the first integral

()()

−+−=

11 3 22 3

constII I II Iεε.

In this case, we can choose the function

()()

=−+−

11 3 22 3

VII I II Iεε

(23.1.82)

as Lyapunov function. Using the same order of the principal moments of inertia, we can

state that

(, )V εε is a positive definite function in the plane of the variables

,εε;

on the other hand,

′

= 0V

, and we can state that the motion of rotation about the

principal axis of minimal principal moment of inertia is stable for the non-linear system

too.

Proceeding analogously with the equations which are obtained taking the

-axis

as axis of rotation, we can show that the motion of rotation about the principal axis of

maximal moment of inertia is stable for the non-linear system too.

Choosing as axis of rotation the principal axis

Ox and maintaining the order

123

III, we write the system of non-linear equations of the perturbed motion in

the form

()( )

()

=− +

=−

=− +

11 2 3 2 2 3

22 3 1 31

33 1 2 3 1

III

εωεε

εεε

εωεε



(23.1.83)

Let us choose the Lyapunov function

1313

VIIεε

;

(23.1.83')

using the equations (23.1.83), we can calculate

()

()()

′

=+ − + −

⎡⎤

⎣⎦

21 2

02 2

2112323

VIIIIIIεω ε ε.

(23.1.83'')

0εω , the instability results – obviously – even from the system of equations

(23.1.83). If

0εω , then

′

is positive definite and we are in the conditions of

Chetaev’s theorem 23.1.16 of instability.

Let us consider now the motion of the heavy rigid solid in the case in which

the centre of mass

C does not coincide with the fixed point O , being in the

Lagrange–Poisson case of integrability (for which

==>

12 3

IIJI

, hence in the

case of an oblate spheroid, the mass centre

123

(,, )C ρρρ being on the

Ox -axis,

== >

12 3

0, 0ρρ ρ ). The corresponding equation of motion (15.2.1) admits the

solution

MECHANICAL SYSTEMS, CLASSICAL MODELS

558

≡≡≡

1233

123

() 0, () 0, () ,

() 0, () 0, () 1.

ttt

ωωωω

ααα

(23.1.84)

for a rotation about the

-axis. Let us introduce the perturbed motion

===+

11223 33

11223 3

,, ,

,,1,

ωεωεωωε

αηαηα η

(23.1.84')

Using the first integral (15.1.44), (15.2.1') and (15.2.1''), we can introduce the

functions (we neglect the constant terms)

()( )

()

=++ + +

=++++

=+++

22 2 0

1123333 33

21123333333

222

3123 3

22,

VJ I mg

VJ I

εε ε ωε ρη

εη εη ε ω η εη

ηηη η

(23.1.84'')

We search now the Lyapunov function in the form

()()

()

002

12 333333 44

202

111 3331

202

222 3332

202

33333 3333

VV V mg I V I V V

JJ mgI

IImgI

λρωλ ωλμ

ελεη ρωλη

με λεη ρ ωλη

=+ − + − + +

=+ − +

++ − +

++ + − +

(23.1.84''')

According to Silvester’s criterion, the first two quadratic forms (with the same

coefficients) are positive definite if and only if their discriminant is positive

()

−+

333

JmgI

λρωλ

hence if and only if

≡+ + <

33 3

() 0PJI mgλλ ωλ ρ ;

(23.1.85)

this is possible only if the zeros of this polynomial are real, hence only if

()

33 3

4IJmgωρ.

(23.1.86)

The last quadratic form in (23.1.84''') is positive definite if and only if

Stability and Vibrations

559

()

+> >

−+

3333

0, 0

ImgI

μλ

λρωλ

hence if and only if

+> + + <

3333

0, 0

IImg

μλωλρ

(23.1.85')

The last inequality is reduced to the inequality (23.1.86) if one chooses

μ in the form

()

−

II J

μ ;

(23.1.86')

in this case,

+= >

μ .

(23.1.86'')

Hence, if the inequality (23.1.86) holds and

μ is given by (23.1.86') then

Lyapunov’s function

V is positive definite for any λ contained between the two zeros

of the polynomial ()P λ . We can thus state that the rotation about the

-axis is

stable with respect to all the variables

123123

,,,,,ωωωααα.

23.1.3.2 Motion of Rotation of a Projectile

We will consider the motion of rotation of a projectile in a grazing case, assuming –

after A.N. Krylov who studied the problem – that its centre of gravity

≡CO

has a

rectilinear and uniform motion, of velocity

v along the horizontal fixed axis

′

Ox .

Thus, we will be in the Lagrange–Poisson case of integrability; the resistance

of the

air, supposed to be constant, will have its point of application on the dynamic axis of

symmetry

. Let

′′

Ox x be the vertical plane in which one shoots and let

′′′

123

Ox x x

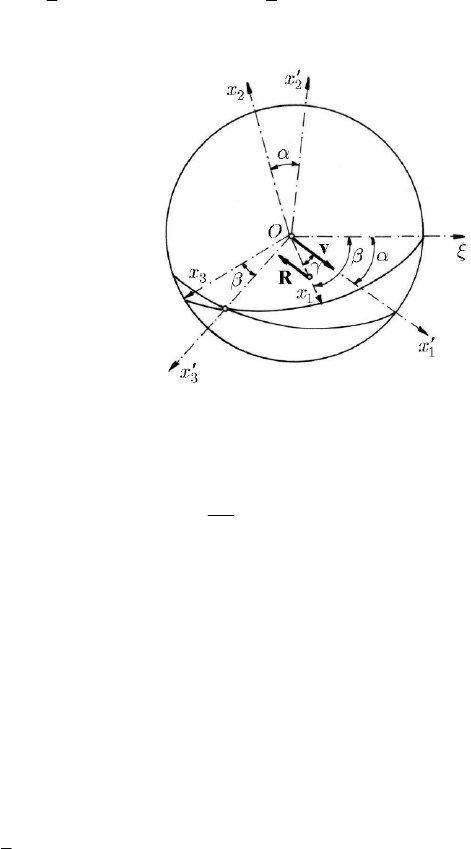
be the inertial frame of reference (Fig. 23.17).

To specify the position of the

-axis, we project it on the plane

′′

Ox x along

Oξ

and denote by

α the angle made by the latter axis with

′

Ox and by β the angle made

by it with

; thus, one passes from the inertial frame of reference

′′′

123

Ox x x to the

non-inertial frame

123

Ox x x

(the axes

′

Ox and

form the angle α and the axes

′

Ox and

form the angle β ). A supplementary rotation of angle ϕ about the axis

allows to pass from the frame

123

Ox x x

to a frame rigidly linked to the rigid solid.

Hence, the generalized co-ordinates are

,αβ and ϕ .

The angular velocity ω of the projectile will thus have the components ,αβ



and ϕ ;

the projections of this velocity on the principal axes of inertia

123

,,Ox Ox Ox are

expressed in the form

MECHANICAL SYSTEMS, CLASSICAL MODELS

560

=+ =− =

123

sin , , cosωϕαβω βωαβ



 

(23.1.87)

The kinetic energy is given by

()

222 222

123

sin cos ,

TIJ I Jωωω ϕαβ βαβ=++= + ++

⎡

⎤

⎡⎤

⎣⎦

⎣

⎦



 

(23.1.88)

Fig. 23.17 Motion of rotation of a projectile

where

is the principal moment of inertia with respect to the axis, while

is the

principal equatorial moment of inertia. Besides the own weight which acts at the gravity

centre

, we apply a force of resistance

of the air, at the centre of pressure A , on

the

Ox -axis, at the distance

=OA l

; we mention that (), constRRvv−=, so that

= constR , the force being along the direction of the

′

Ox -axis, in a sense opposite to

that of the velocity v . If we denote by

γ the angle made by the axes

′

Ox and

Ox ,

then the moment of the force

R with respect to the centre O will be given by sinRl γ

(in modulus), resulting the elementary work

==−dsindd(cos)WRl Rlγγ γ; the

potential energy can be written in the form

−= =cos cos cosURl Rlγγβ

(23.1.88')

where we took into account that the arcs

,,αβγ form a rectangular spherical triangle

with

γ as hypotenuse. We obtain the first integral of energy

()

222

sin cos cos cos , const.

IJ Rlhhϕα β β α β α β+++ + ==

⎡⎤

⎣⎦



 

(23.1.89)

We notice that the generalized momentum

Iω

is constant, because the generalized

co-ordinate

ϕ is cyclic (does not intervene in

=−HTU

); we can thus eliminate the

Stability and Vibrations

561

term

+(sin)I ϕα β from the first integral (23.1.89) (we notice that

+=sin constϕα β is the projection of the angular velocity of the rigid solid on the

axis along which advances the mass centre).

The components of the moment of momentum with respect to the pole

O , along the

axes of the non-inertial frame of reference, are

===

123

OOO

KIKJKJωωω,

so that we can write a second first integral (the component of the moment of momentum

along the

′

Ox -axis) in the form

() ()

()

11 12

13 1 2 3

cos , cos ,

cos , cos cos sin cos sin

cos cos sin cos cos sin const,

K K Ox Ox K Ox Ox

KOxOxI J J

ωαβωαωαβ

ωαβ βαααββ

′

′′

′

+=−−

=+− =



(23.1.89')

where we have used the fact that the arcs

+,/2αβ π and

′

(, )xx form a rectangular

spherical triangle with sides

α and /2βπ+ , the hypotenuse of which is given by

cos( , ) cos cos( /2) cos sinxx αβπ αβ

′

=+=−

The total derivatives with respect to time of these first integrals are – obviously – zero.

Expanding into series after the power of the variables

α and β , we can introduce

the functions

()()

()

()()

()

=+− +

22 22

,,, ,

,,, .

VJRl

VJ I

αβαβ α β α β

αβαβ βα αβ ω α β



(23.1.90)

We set up a Lyapunov function of the form

=−

VV Vλ

, so that

() ()

2222

22.

VJ J I Rl J J I Rlαλαβωλβ βλβαωλα=++− +−+−

⎡⎤⎡⎤

⎣⎦⎣⎦



(23.1.90')

We notice that the two expressions in the rectangular brackets have similar forms, i. e.

()

±− − +

Jx y y J I Rlλλωλ;

indeed, for

, xyαβ==

and the sign

we obtain the first bracket, while for

, xyβα==



and the sign – we get the second bracket. This form is positive definite

if the condition

−+<

0JI Rlλωλ

(23.1.91)