Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

532

where

, 1,2,...,

knλ = , are its n zeros. Then, let us replace λ by iω and let us

make

ω vary from −∞ to ∞ ; the increase of the angle = arg ( i)

Pθω is given by

∞∞

−∞ −∞

=−

∑

() arg(i )

Δθω Δ ω λ .

We notice that (we assume that no one of the roots is on the imaginary axis)

∞

−∞

⎧

⎪

−=

⎨

−>

⎪

⎩

for 0,

arg(i )

for 0.

πλ

Δωλ

πλ

Denoting by

n and

n the number of zeros at the left and at the right of the imaginary

axis, respectively (

nn n), it results

()

∞

−∞

=−()

nnΔθω π.

Let us consider the hodograph (curve) described by the affix of the complex number

(i)

P ω , when ω varies from −∞ to ∞ ; this hodograph has two branches: one for

> 0ω

and one for

< 0ω

, the two branches being symmetric with respect to the real

axis, because

(i)

P ω and −(i)

P ω are complex conjugate numbers. Denoting by

∞

the increase corresponding to the variation of

ω from 0 to ∞ , we obtain

()

∞∞

−∞

==−

() ()

nnΔθω Δ θω π.

= 0

n and = 0

n , when all the zeros are situated at the left of the imaginary

axis. We can thus state

Theorem 23.1.5 (geometrical criterion). All the zeros of the polynomial ()

P λ

(non-lacunary and with all coefficients positive) have their real part negative if and

only if the hodograph of the polynomial

(i)

P ω , for ω varying from 0 to ∞ , does not

pass through the origin (so that

()

P λ does not have purely imaginary zeros) and if

the condition

∞

()

Δθω π

(23.1.41)

is fulfilled.

We notice that for a stable polynomial (called Hurwitz polynomial too) the argument

has a monotone variation when

ω varies from 0 to ∞ .

This criterion has been applied by Mikhailov to the study of the systems with control

function; this criterion is called Mikhailov’s criterion too.

Stability and Vibrations

533

23.1.1.7 Instability of Equilibrium. Lyapunov’s and Chetaev’s Theorems

In 1892, in his famous doctor thesis “General problem of the stability of motion”,

A.M. Lyapunov has put the problem of the reciprocal of the Lagrange-Dirichlet

theorem, problem which was not yet completely solved; other studies have been made

by N.G. Chetaev (Lyapunov, A.M., 1949; Chetaev, N.G., 1963).

Let us return to the notations in Sect. 23.1.1.3 and let us suppose, further, that

... 0

qq q==== and (0,0,...,0) 0U = for the position of equilibrium. Let be

an expansion of the potential function into a power series after the generalized

co-ordinates

12 112

( , ,..., ) ( , ,..., ) ...

ms s

U U qq q U qq q

=+ +,

(23.1.42)

where

(,,..., )

UUqq q= is a homogeneous function of degree

, 1,...kmm=+, and

U is not identical to zero and where the smallest term of the

expansion corresponds to

2m ≥ , because at the origin

(/) 0

Uq∂∂ =, this one

being a position of equilibrium.

Let us expand into a power series, with respect to the generalized co-ordinates, the

coefficients

( , ,..., )

jk jk

ggqqq= of the expression (23.1.14) of the kinetic energy

; we denote

(1/2)

Tgqq= , where

(0, 0,...,0)

gg= . It results

,TT UU=+ =+OO,

(23.1.43)

where

O represents the terms of higher order with respect to the generalized

co-ordinates and the generalized velocities, respectively. Because

T is a positive

definite quadratic form with constant coefficients, there exists a transformation of

co-ordinates

, 1,2,...,

jiji

qj sηα==, so that – simultaneously – the two quadratic

forms be reduced to two sums of squares, i. e.

kkk

TUηλη

=+= +

∑∑

 OO,

(23.1.43')

where the coefficients

, 1,2,...,

ksλ = , are given by the secular equation

det 0

jk k jk

agλ−=

⎡⎤

⎣⎦

;

(23.1.43'')

there exists at least one

λ < , because the quadratic form

U can take some negative

values too. The co-ordinates

η are called normal co-ordinates or principal

co-ordinates. Lagrange’s equations in normal form (written by means of the normal

co-ordinates) are of the form

(!), 1,2,...,

kkk

ksηλη=− + = O .

(23.1.43''')

MECHANICAL SYSTEMS, CLASSICAL MODELS

534

Let be the auxiliary quadratic form (

V does not represent the potential energy)

()

22 2

11 ,

22 2

kkk k kkk k k

μμ

ελλημληη λη

⎡⎛ ⎞ ⎛ ⎞ ⎤

=− + + + − + + +

⎜⎟ ⎜⎟

⎢⎥

⎣⎝ ⎠ ⎝ ⎠ ⎦

∑



(23.1.44)

where

1for 0,

−<

⎧

⎪

⎨

≥

⎪

⎩

(23.1.44')

with

1,2,...,ks= and 0μ > . It is easy to see that

()

kk k k

μμ

μελ η η

−−

⎡

⎛⎞ ⎤

=+++

⎜⎟

⎢

⎥

⎣

⎝⎠ ⎦

∑

 O ,

(23.1.44'')

for a mechanical system in motion. Without any loss of generality, let us assume that

0λ < ,

λ being the negative number with the greatest modulus; we choose 0μ > ,

so that the conditions

111

0, 0

μμ

λλλ+< ++>

be fulfilled. In this case, the sum in the expression (23.1.44'') is a positive definite

quadratic form. If we choose, in a

Δ -neighbourhood,||,

ηΔ< ||

ηΔ< ,

1,2,...,ks= , hence quantities sufficiently small in absolute value, then it results

()

μ−

> ,

wherefrom

()

V>V e

ttμ −

(23.1.44''')

with

()Vt V= . Let us take all the initial values equal to zero, excepting

η , which

will be taken so that

||ηΔ< . From (23.1.44) and from the second condition put

above, it results

0V > , the motion being in the limits of the considered

Δ -neighbourhood, as small could be

||η

; otherwise, from (23.1.44''') would result

lim

→∞

=∞, even if the quadratic form V is bounded in this Δ -neighbourhood.

We can thus state

Theorem 23.1.6 (Lyapunov; first theorem). If the potential energy

( , ,..., )

Uq q q− of

a conservative discrete mechanical system has not a minimum at a position of

Stability and Vibrations

535

equilibrium, which is put into evidence from the quadratic form

212

( , ,..., )

Uqq q of the

expansion (23.1.42) (hence,

2, mU= having negative terms – may be ones of them

are positive), then the respective position of equilibrium is instable.

For

2m > in the expansion (23.1.42), without proof, we state

Theorem 23.1.7 (Lyapunov; second theorem). If the potential energy

( , ,..., )

Uq q q−

of a conservative discrete mechanical system has a local maximum for

...qq==

q==, which can be shown starting from the term

(,,..., )

Uqq q, 2m ≥ , with

the smallest power (in a neighbourhood of the origin, excluding the origin,

U−<,

which is possible only if

m is even) in the expansion (23.1.42), then the position of

equilibrium is instable.

As well, we state

Theorem 23.1.8 (Chetaev). If the potential energy

( , ,..., )

Uq q q− of a conservative

discrete mechanical system is a homogeneous function in the generalized co-ordinates

and if at the position of equilibrium

... 0

qq q==== does not take place a

minimum, then this position is instable.

Let be, e. g.,

... , const

UCqqqC==; Chetaev’s theorem shows that the origin

is an instable position of equilibrium.

23.1.1.8 Asymptotic Stability of Equilibrium. Dissipative Discrete Mechanical

Systems

The notion of asymptotic stability has been introduced in Sect. 23.1.1.1. Thus, a

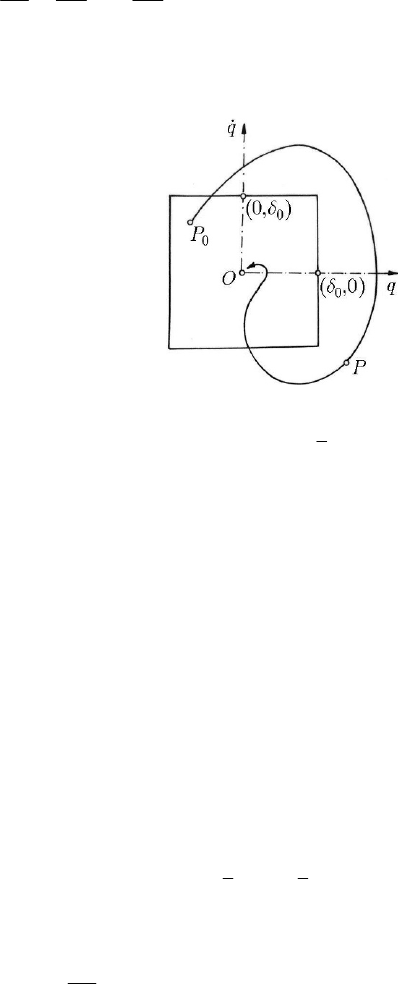
position of equilibrium is called asymptotically stable if it is stable and if, for values (in

modulus) sufficiently small of the initial generalized co-ordinates and of the generalized

velocities, all the generalized co-ordinates and the generalized velocities tend to zero

when the time

t increases indefinitely, hence if it exists a number

0δ > so that

lim ( ) 0, lim ( ) 0, 1,2,...,

qt qt j s

→∞ →∞

===

(23.1.45)

when the inequalities

, , 1,2,...,

qqj sδδ<<= ,

(23.1.45')

hold. The phenomenon is graphically illustrated in Fig. 23.12 for

1s =

in the space

(,)qq .

Let be a holonomic and scleronomic discrete mechanical system subjected to the

action of some potential generalized forces

/ , ( , ,..., )

UqUUqq q∂∂ = and of some

non-potential generalized forces

12 12

( , ,..., , , ,..., ), 1,2,..,

QQqq qqq qj s==  , of

the form (23.1.13'). Lagrange’s equations can be written in the normal form (18.2.47'),

hence in the form

12 12

( , ,..., , , ,..., ), 1,2,...,

qGqq qqq qj s==    .

(23.1.46)

MECHANICAL SYSTEMS, CLASSICAL MODELS

536

The total derivative with respect to time to the mechanical energy

12 12

( , ,..., , , ,..., )

EEqq qqq q=   is given by

12 12

( , ,..., , , ,..., )

EE E

qGEqqqqqq

tq q

∂∂

′

=+ =

∂∂





;

(23.1.47)

hence, at each point of the space

12 12

( , ,..., , , ,..., )

qq qqq q , not only the mechanical

energy has a finite value, but also its total derivative with respect to time.

Fig. 23.12 Graphical representation of asymptotic stability in the phase plane

If the non-conservative generalized forces

Q are dissipative, then their power is

negative (see Sect. 18.2.1.3). In this case,

d/d 0Et≤ if the discrete mechanical

system is in motion, so that the function

is non-positive in the domain of the space in

which the motion takes place; one has equality only in the case in which the generalized

velocities vanish

( ... 0)

qq q====  . Let us suppose that the position of

equilibrium of the discrete mechanical system is isolated, hence that in the

neighbourhood there are not other positions of equilibrium. One can state

Theorem 23.1.9. If the potential energy

U−

of a dissipative holonomic and

scleronomic discrete mechanical system has a strict minimum for an isolated position

of equilibrium, then this position is asymptotically stable.

Let us consider again the case of a damped linear oscillator of equation (23.1.38),

considered in Sect. 23.1.1.5, written in the form

0, , , 0mx k x kx m k k

′′

++= >  ;

the mechanical energy is given by

Emx kx=+

wherefrom

()

mxx kxx mx kx x k x

′

=+=+ =−<    

Stability and Vibrations

537

Hence, the oscillator is dissipative, the position of equilibrium being isolated, as it results

from the equation of motion; using the Theorem 23.1.9, we can state that the position of

equilibrium is asymptotically stable, as it has been shown in Sect. 23.1.1.5 too.

To generalize the Lagrange-Dirichlet theorem, Lyapunov replaces the mechanical

energy

E by any function

12 12

( , ,..., , , ,..., )

VVqq qqq q=   of class

C (with respect

to the generalized co-ordinates and to the generalized velocities), which has a minimum

at the position of equilibrium and which does not increase for any motion of the

mechanical system. Let us calculate the total derivative with respect to time

12 12

( , ,..., , , ,..., )

VV V

qGVqqqqqq

tq q

∂∂

′

=+ =

∂∂





(23.1.48)

Observing that

0, 1,2,...,

qq j s== = , at the origin, the function V

′

vanishes

at this point. Because

V does not increase for any motion, we have d/d 0VtV

′

=≤,

so that

′

has a maximum at the position of equilibrium; if this maximum is a local

one, then in the neighbourhood of the origin (excepting the point

O ) we have 0V

′

< ,

so that at the origin the function

V is strictly decreasing. One can now follow the proof

given to the Lagrange-Dirichlet theorem, replacing the function

E by the function V .

Thus, one can state

Theorem 23.1.10 (Lyapunov). Knowing the position of equilibrium of a holonomic and

scleronomic discrete mechanical system, subjected to the action of forces which do not

depend explicitly on time, if there exists a function

12 12

( , ,..., , , ,..., )

Vq q q q q q  of class

C which has a strict extremum at the position of equilibrium and if the derivative V

′

with respect to time (calculated by means of the equations of motion) has an extremum

of opposite type, at the same position of equilibrium, then this position is stable. If the

extremum of the derivative is strict too, then the position of equilibrium is

asymptotically stable.

We notice that, in the formulation of the stability criterion, the words “minimum”

and “maximum” can be interchanged, because one can replace the function

V by the

function

V− , which leads to the previous formulation. The function V is called

Lyapunov’s function.

23.1.2 Stability of Motion

In what follows, one makes a general study of the problem by the stability of the

motion, with the aid of Lyapunov’ function. A special attention is given to the systems

with cyclic co-ordinates and to the limit cycles. We mention also the case of

rheonomous systems (Lyapunov, A.M., 1949).

23.1.2.1 General Problem of the Stability of Motion. Lyapunov’s Theorems

The stability of the position of equilibrium of a discrete mechanical system is put in

evidence, in general, by the inequalities (23.1.1), (23.1.1'). But if these inequalities take

place only for some generalized co-ordinates

, ,...,

qq q and generalized velocities

MECHANICAL SYSTEMS, CLASSICAL MODELS

538

, ,...,

qq q  or, more general, for some functions of these variables

12 12

( , ,..., , , ,..., ), 1,2,...,

xxqq qqq qi n==  ,

(23.1.49)

chosen so that

(0,0,...,0,0,0,...,0) 0

x = , then we have to do with a problem of

conditioned stability; we assume that these new functions verify the non-autonomous

system of differential equations of first order

( , ,..., ; ), 1,2,...,

Xxx xt i n

(23.1.49')

where

X are functions of class

in the domain

, , 1,2,...,

xtti nΔ≤≥= ,

(23.1.49'')

t being the initial moment.

To the position of equilibrium correspond

, 1,2,...,

xi n= , which implies the

conditions

(0,0,...,0; ) 0, 1,2,...,

Xtin≡= .

(23.1.49''')

The stability problem of the null solution imposes the existence of

() 0δδε=> for

any

0ε > , so that if

( ) , 1,2,...,

xt i nδ<= ,

(23.1.50)

then the inequalities

() , 1,2,...,

xt i nε<= ,

(23.1.50')

must take place for any

tt≥ .

In the case of asymptotic stability, there must exist

0δ > so that

lim ( ) 0, 1,2,...,

xt i n

→∞

== ,

(23.1.51)

( ) , 1,2,...,

xt i nδ<= .

(23.1.51')

In the case of a problem of non-conditioned stability of the position of equilibrium,

one can take as variables

, 1,2,...,

xi n= , the generalized co-ordinates and the

generalized velocities; thus, the system (23.1.49') becomes Lagrange’s system of

Stability and Vibrations

539

equations (18.2.29), written in the form of a system of differential equations of first

order. If we take these variables as generalized co-ordinates and generalized moments,

then one obtains Hamilton’s equations (19.1.14).

Let be two important cases of functions , 1,2,...,

Xi n= :

(i) The stationary case in which

t does not appear explicitly in these functions

0, 1,2,...,

Xin

∂

===

∂



(23.1.52)

the equations being autonomous.

(ii) The periodic case, of period

with respect to the temporal variable t , for which

+= =

12 12

( , ,..., ; ) ( , ,..., ; ), 1,2,...,

Xxx xt Xxx xti nτ

(23.1.52')

By a demonstration analogue to that used for the Lagrange-Dirichlet theorem, one

obtains an extension of the Theorem 23.1.10. Thus, we state

Theorem 23.1.11 (Lyapunov). If, in case of the stationary or periodic system of

differential equations of first order (23.1.49'), there exists a function

( , ,..., ; )

Vx x x t

of class

C in the domain (23.1.49''), which – for t considered as a parameter – has a

strict extremum at the point

0, 1,2,...,

xi n== , and if, at the same point and at any

moment

t , its total derivative with respect to time

(,,..., ;)

Vxx xt X

∂∂

′

∂∂

∑

(23.1.53)

has an extremum of opposite type, then the null solution of the system is stable. If the

extremum of the derivative

′

is strict too, then the solution is asymptotically stable.

In a stationary case, the function

V cannot depend explicitly on time, while in a

periodic case, it must be periodic too, of the same period

τ as the functions

, 1,2,...,

Xi n= .

In the general case (non-stationary and non-periodical) Lyapunov’s function

must

fulfill more rigorous conditions.

Let us consider a particular case in which one can use the Theorem 23.1.11 for a

simple (non-asymptotic) stability. Let us suppose that the function

( , ,..., ; )

Vx x x t

is a first integral of the system of equations (23.1.49'), hence that it becomes a constant

(independent of

), after replacing the variables

, 1,2,...,

xi n=

, by a solution of this

system; in this case

d/d 0VtV

′

== has an extremum at the origin for any t .

Starting from the Theorem 23.1.11, we can state

Corollary 23.1.1. If the system of differential equations (23.1.49') admits a first

integral

( , ,..., ; )

Vx x x t which has a strict extremum at

... 0

xx x====

for any fixed

t , then this solution is stable.

MECHANICAL SYSTEMS, CLASSICAL MODELS

540

In a stationary case, Lyapunov’s function does not depend explicitly on time, while

in a periodic case this function is periodic with respect to time, of period

τ .

As we have seen in Sect. 23.1.1.1, the study made on the system of differential

equations (23.1.49') is equivalent to a study on the system of equations of perturbed

motions, of the form (23.1.7), hence it is equivalent to a study on an arbitrary system of

differential equations of first order (e. g., of the form (23.1.6)).

The Theorem 23.1.11 can be thus used not only to the study of the stability of a

position of equilibrium, but also to the study of the stability of motion.

23.1.2.2 Stability of Systems of Non-linear Differential Equations

We consider the system of non-linear differential equations (23.1.29), being limited

to the autonomous case; as in Sect. 23.1.1.1, we use the notation

22 2

() () () ... ()

txtxt xtρ =+++.

(23.1.54)

The mechanical systems which lead to such systems of differential equations are

scleronomic ones.

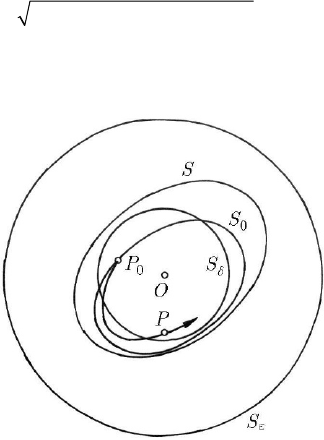
Fig. 23.13 Graphical representation of the stability problem of autonomous systems

of non-linear differential equations

Let be a function

( , ,..., )

Vx x x positive definite (otherwise, one considers – for the

proof – the function

V− ); we assume that in the spherical domain ()thρ ≤ we have

0V > and 0V

′

≤ . As well, let be also the sphere S

, specified by

() ,0thρεε=<<, contained in the sphere

S , of equation ()thρ = (Fig. 23.13). We

denote by

l the inferior bound of the function V on S

, so that, on this sphere,

0Vl≥>. The surface S of equation () , 0Vt C C l=<<, will, obviously, be

interior to the sphere

. Let be also the number δ sufficiently small, so that S

equation

()tρδ= be interior to the surface S , non having any common point with this

Stability and Vibrations

541

one (which is possible, because

S does not pass through the origin, having 0V > ).

Observing that

0V ≤



(see Sect. 23.1.1.2), the trajectory of the representative point P ,

which starts from the initial position

P , interior to the sphere S

, does not pierce the

surface

S , specified by the equation

()Vt V= ; having

VC< , the surface

S is

interior to the surface

, the trajectory of the point

being thus interior to this surface.

We can state

Theorem 23.1.12 (Lyapunov; first theorem of stability). If for a system of non-linear

differential equations (23.1.29) (of the perturbed motion), we can build up a function

( , ,..., )

Vx x x of definite sign, for which – due to the system – the derivative V

′

is a

function of constant sign, opposite to the sign of

V , or is identically zero, then the

non-perturbed motion (the trivial solution) is stable.

We use previous notations and assume that

′

< (strict inequality); in this case,

the function

()Vt is strictly monotonically decreasing and inferior bounded (by zero).

Hence

lim ( ) 0

Vt α

→∞

=≥. In the closed domain contained between the surfaces

VV=

and

V α=

(we suppose that

0α ≠

) the negative function V

′

has a superior

bound

(0)ll−>; we have 0l ≠ because V

′

is negative definite (it vanishes only at

the origin). It results

′

≤− in the mentioned domain, for any t ; in this case, the

identity

VV Vt

′

−=

∫

leads to

()VV ltt≤−−. For t sufficiently great, V

becomes negative, which contradicts the hypothesis according to which

0V > . Hence,

one can have only

= 0α

. Thus, we state

Theorem 23.1.13 (Lyapunov; second theorem of stability). If, for the system of

non-linear differential equations (23.1.29) (of the perturbed motion) we can build up a

function

( , ,..., )

Vx x x of definite sign, for which – due to the system – the

derivative

′

is a function of definite sign (not only of constant sign), opposite to that

V , then the unperturbed motion (the trivial solution) is asymptotically stable.

This theorem gives sufficient conditions of asymptotic stability for small initial

perturbations. Barbashin and Krasovski gave sufficient conditions of asymptotic

stability for any initial perturbations.

As we have seen in Sect. 23.1.1.7, a study of the instability of equilibrium, hence of

the motion too, is – as well – important; a proof, analogue to those previously given,

allows to state.

Theorem 23.1.14 (Lyapunov; first theorem of instability). If, for the system of

non-linear differential equations (23.1.29) (of the perturbed motion), we can build up a

function

( , ,..., )

Vx x x for which – according to the system – the derivative V

′

is a

function of definite sign, the function

V being not of constant sign (and opposite to that

′

), then the unperturbed motion is instable.

We can state also

Theorem 23.1.15 (Lyapunov; second theorem of instability). If, for the system of

non-linear differential equations (23.1.29) (of the perturbed motion) we can set up a

function

( , ,..., )

Vx x x , so that – according to the system – to obtain a derivative