Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

502

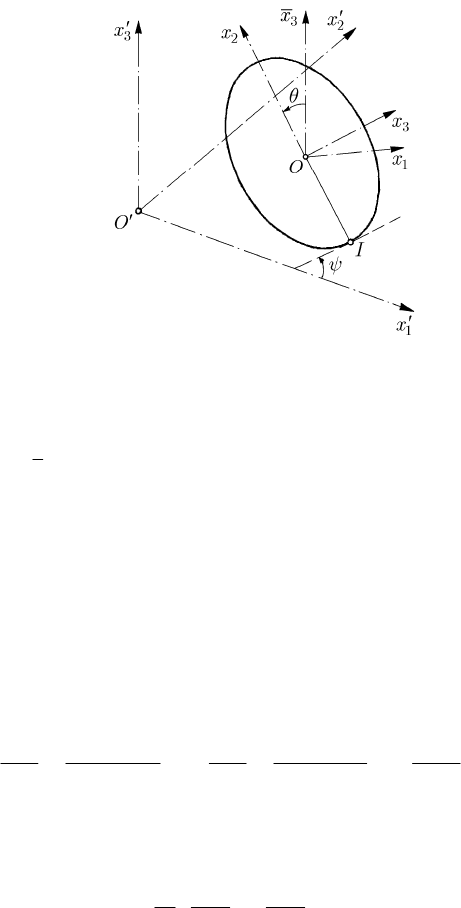
We introduce the generalized co-ordinates

′′

== = = =

12 4 41 2

,,, ,qq q qxqxθϕψ , the

mechanical system having

−=52 3 degrees of freedom. We choose the angles , θψ and

ϕ as independent co-ordinates and notice that the constraint relations do not contain the

generalized co-ordinate

θ ; we can thus write an equation of Lagrange corresponding to this

generalized co-ordinate.

Fig. 22.20 Motion of a circular disc, which rolls without sliding on a fixed horizontal plane

Taking into account (22.4.28), we find Lagrange’s functions in the form

()( )

()

⎡

=+ ++ −

⎣

+−

⎤

⎦

*222

sin

cos cos ,

JMR I MR

JMgR

θϕψθ

ψθ θ





(22.4.29)

where

IIJ and

I are the central principal moments of inertia of the disc, while

gM is its weight.

Comparing the constraint relations (22.4.28) to the relations (22.2.88), we get

42 52

cos , sincR cRψψ,

the other coefficients being equal to zero; we notice that

() ()

∂∂

=====

∂∂ ∂∂ ∂

42 52

cos sin

0, 0, 0

qqql

ψψ

θθ

so that the relations (22.4.17) are verified. In this case, Chaplygin’s equation is reduced to

Lagrange’s equations

⎛⎞

∂∂

−=

⎜⎟

∂

⎝⎠

dt θ



Dynamics of Non-holonomic Mechanical Systems

503

which takes the form

()( )

()

+++ −

+−=

sin cos

sin cos sin 0,

JMR I MR

JMgR

θϕψθψθ

ψθθ θ

  



but we cannot write analogous equations corresponding to the generalized co-ordinates

and

ϕ .

We notice also that, in this case, the generalized co-ordinate

θ is not an ignorable

co-ordinate, because the kinetic potential

L depends explicitly on θ . But we can write a

first integral of the mechanical energy in the form

()( )

()

22 2 2 2

sin cos 2 cos 2 ,JMR I MR J MgR hθϕψθψθθ+++−+ + =





(22.4.30)

where

is the energy constant, which is determined by the initial conditions.

Let us consider now also the free motion of a homogeneous sphere, of radius

R and

mass

, on a horizontal plane

′′′

Oxx , the

′′

Ox -axis being directed towards the part

where is the sphere, the constraint relations being given by

12 21

0, 0xR xRωω

′′ ′′

−= −=

(22.4.31)

We introduce the quasi-velocities

1234

,,,,πππππ by means of the relations (see the

relations (5.2.35'))

()

′

≡= +

′

≡= −

′

≡= +

′

=− −

′

=+ −

cos sin sin ,

sin sin cos ,

cos ,

sin sin cos ,

cos sin sin ,

πωθψϕθψ

πωϕθψ

πθψϕθψ





















(22.4.32)

where we have used Euler’s angles

, θψ

and ϕ ; hence, it results

=− + +

=−

′

=−

′

=− −

12 3

124

sin cot cos cot ,

cos sin ,

sin cos

sin sin

ψπψθπ ψθπ

θπ ψπ ψ

πψπ ψ

θθ

ππ



 









(22.4.32')

Taking into account these relations, the kinetic energy

MECHANICAL SYSTEMS, CLASSICAL MODELS

504

()

′′ ′′′

=++++

⎡⎤

⎣⎦

222222

12 1 2 3

TMxxiωωω

(22.4.33)

where

i is the gyration radius with respect to a diameter of the sphere, takes the form

()()

()

=−+−+++

⎡⎤

⎣⎦

*2222

24 1 123

TMR R iππ ππ πππ  

(22.4.33')

It results thus

()

∂

=+−

⎡⎤

⎣⎦

∂

=+−

⎡⎤

⎣⎦

∂

∂∂

==−

∂∂

∂

=− −

∂

324

MR i R

Mi M R

ππ

πππ

ππ















The non-zero coefficients

γ are

11 22 33

23 32 31 13 12 21

1, 1, 1γγ γγ γγ=− = =− = =− = ,

44 55

13 31 23 32

, RRγγ γγ=− = =− = . The condition (22.4.21) is verified, as one can see

by a direct calculation. We notice also that

T does not depend explicitly on the

quasi-co-ordinates, so that the quasi-co-ordinates

π ,

π and

π are ignorable (they are

hidden too); the equations (22.4.20) lead to the first integrals (

, the potential

energy being constant in the motion on a horizontal plane)

∂∂∂

===

∂∂∂

***

123

const, const, const

TTT

πππ

(22.4.34)

Putting

0ππ

, which corresponds to the constraint relations (22.4.31), we notice

that the first integrals (22.4.34) lead to

′′′

== == ==

11 22 33

const, const, constπω πω πω.

(22.4.35)

Taking into account the constraint relations (22.4.31), the kinetic energy (22.4.33) takes

the form

()( )

′′ ′

=+++

⎡⎤

⎣⎦

*222222

12 3

TMRi iωω ω

;

(22.4.36)

one obtains thus the first integral of the mechanical energy

()( )

′′ ′

+++=

22 2 2 22

12 3

Ri i

ωω ω

(22.4.37)

the energy constant

h being determined by initial conditions.

Chapter 23

Stability and Vibrations

Some problems of stability of equilibrium and motion have been put in evidence, in

an incipient form, in the frame of Newtonian mechanics, in several of the preceding

chapters; but these problems need a more profound study, with a general character, in

the frame of Lagrangian or Hamiltonian mechanics. The motion of a mechanical system

S can take the form of linear or even non-linear vibrations; the corresponding

mechanical phenomenon needs a thorough study in a general form too.

After a study of the stability of discrete mechanical systems, one considers the

vibrations with a deterministic character of these systems. The corresponding

mechanical phenomena are linked between them, the vibrations around a stable position

of equilibrium playing a very important rôle.

23.1 Stability of Mechanical Systems

In the study of the behaviour of a mechanical system S , at rest with respect to an

inertial frame of reference, appears also the notion of stability, at a small change of its

configuration of equilibrium. In a qualitative definition, if the mechanical system

returns to its initial configuration, then the position of equilibrium is stable; otherwise,

it is instable. A first study for a particle has been made in Sects. 4.1.1.7 and in 7.2.3.

The respective problems are extended to the motion of a discrete mechanical system,

case in which intervene also the velocities of the particles at an initial state, which must

be maintained in certain limits to can speak about the stability of the motion. A study in

the frame of Hamiltonian mechanics, in the phase space

, is interesting in this order

of ideas.

We will make, in what follows, a study of the stability of equilibrium and motion,

followed by various applications.

23.1.1 Stability of Equilibrium

After some introductory notions, we present the Lagrange–Dirichlet theorem and the

theorems of Lyapunov and Chetaev. Thus, important criteria concerning the stability of

equilibrium are given. We mention a detailed study of the linear systems too

(Chetaev, N.G., 1963; Lyapunov, A.M., 1949).

505

P.P. Teodorescu, Mechanical Systems, Classical Models,

MECHANICAL SYSTEMS, CLASSICAL MODELS

506

23.1.1.1 Introductory Notions

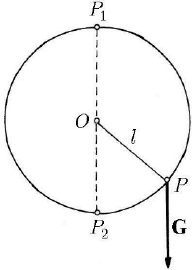
To fix the ideas, we start from a very simple particular case, that is the case of a

particle

of weight G , constrained to stay on a fixed smooth circle, situated in a

vertical plane (Fig. 23.1) (see Sects. 4.1.1.5 and 4.1.1.7 too); we have to do with an

ideal constraint. The positions of equilibrium are

P and

P . The problem is put

analogously in case of the mathematical pendulum (see Sect. 7.1.3.1).

By a small perturbation of the position of equilibrium

P , that is by a displacement

of the particle

P in a position sufficiently close to

P and imparting to it an initial

velocity of sufficiently small intensity, one obtains a motion in which the particle

P :

(i) remains in an arbitrarily small neighbourhood of the position of equilibrium

P ;

(ii) the kinetic energy (hence, the modulus of the velocity of the particle) remains

inferior to an as small as we wish quantity. The properties (i) and (ii) characterize the

stability of the position of equilibrium

P .

Fig. 23.1 Positions of equilibrium of a heavy particle on a smooth circle in a vertical plane

These ideas can be correspondingly generalized for a discrete mechanical system

(we will consider such systems in what follows), the position of which is specified by a

representative point

P in the configuration space

Λ or in the phase space

Γ . Thus,

we say that a position of equilibrium of a discrete mechanical system

S is stable if,

after a sufficiently small perturbation of the corresponding representative point

P , with

sufficiently small arbitrary velocities, so that the magnitude of the kinetic energy of the

mechanical system

S be sufficiently small, it results a motion in which the

representative point

P occupies a position in a as small as we wish neighbourhood with

respect to the position of equilibrium, while the magnitude of the kinetic energy (hence,

the magnitude of the velocities of all particles (or of all rigid solids which form the

system) of the mechanical system

S ) remains inferior to an arbitrary small limit.

Otherwise, if the representative point

P leaves a neighbourhood of the position of

equilibrium or if the kinetic energy of the mechanical system

S is greater than a

positive number which does not depend on the initial conditions (hence, the magnitude

of the velocities of some of the particles have this property too), then the positions of

equilibrium is instable.

Stability and Vibrations

507

Returning to the problem previously considered, we see that the point

P is an

instable position of equilibrium (Fig. 23.1). As a matter of fact, this position is called

labile; if the radius of the circle tends to infinity, the circle becoming a horizontal

straight line, then the position of equilibrium is indifferent (also instable).

In general, we say that a position of a discrete mechanical system S is a position of

equilibrium if, at the initial moment, it had this position, with null velocities, and

remained – further – in the same position; obviously, this is valid for the representative

point

P too.

Let us suppose that the position of equilibrium is specified by the generalized

co-ordinates

, ,...,

qq q; corresponding to the first principle of Newton, the

generalized forces must vanish (

0, 1,2,...,

Qj s== ) in this case. The generalized

velocities

, ,...,

qq q  must vanish too at the initial moment. If the generalized forces

depend, in general, both on the generalized co-ordinates and on the generalized

velocities (

12 12

( , ,..., , , ,..., ), 1,2,...,

QQqq qqq qj s== 

), then the generalized

co-ordinates must correspond to the position of equilibrium, while the generalized

velocities must vanish. Without any loss of generality, we can choose the origin of the

co-ordinates just at the position of equilibrium of the representative point

P (the

equilibrium taking place for

====

... 0

qq q ); the non-zero generalized

co-ordinates of any other position of the representative point

P characterize a deviation

from the position of equilibrium, being called perturbations of the discrete mechanical

system

S .

The position of equilibrium is called stable position of equilibrium if, for initial

perturbations

sufficiently small and for initial generalized velocities

, 1,2,...,

qj s=

sufficiently small too (at the moment

tt), the mechanical system S does not leave an

arbitrary small neighbourhood, having – as well – arbitrary small velocities, in all the period

of motion. More precisely, if – for an arbitrarily given

> 0ε – one can determine

(, ) 0tδδε , so that for ≥

tt the inequalities

<<=( ) , ( ) , 1,2,...,

qt qt j sεε ,

(23.1.1)

take place, assuming that at the initial moment

hold the inequalities

<<=

( ) , ( ) , 1,2,...,

qt qt j sδδ ,

(23.1.1')

then the position of equilibrium

===0, 0, 1,2,...,

qq j s , is stable; obviously,

without any loss of generality, we can take

0t . It is convenient to give a geometric

representation to the inequalities (23.1.1), (23.1.1') in a

2s -dimensional space

12 12

, ,..., , , ,...,

qq q qq q . In the particular case = 1s , let be two vicinities of the

origin

O , corresponding to the mentioned inequalities, in the plane (

,qq ) (Fig. 23.2).

If the point

O corresponds to a stable position of equilibrium and if for a given > 0ε

one chooses a corresponding

> 0δ , then any motion which starts at the moment

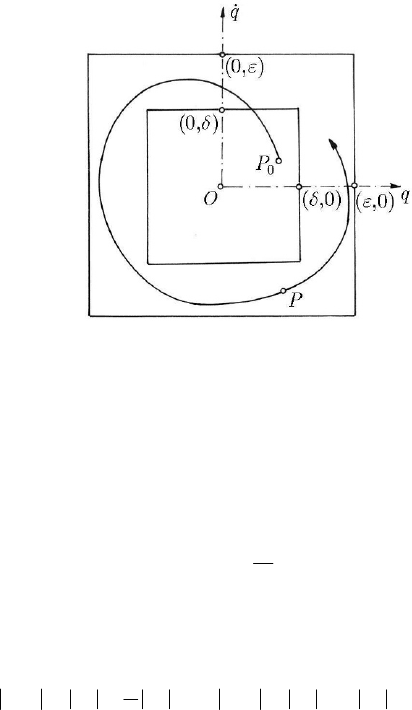
MECHANICAL SYSTEMS, CLASSICAL MODELS

508

t from the interior of a square of centre O and side 2δ remains in the interior of a

square which has the same centre and is of side

2ε .

Fig. 23.2 Motion around a stable position of equilibrium in a phase plane

Let be, for instance, the case of a non-damped linear oscillator, which leads to a

linear differential equation of the form (see Sect. 8.2.2.1 too)

0qqω ;

(23.1.2)

putting the initial conditions

0000

() ,()qt q qt q, it results

00 0

0000

() cos ( ) sin ( ),

() cos ( ) sin ( ).

qt q t t t t

qt q t t q t t

ωω

=−+−

=−−−





(23.1.2')

In this case

≤+ < ≤+ <

00 00

() , ()qt q q qt q qεωε



(23.1.2'')

only if

||q δ and <

||q δ , where we choose, e.g., = min( /2 , /2)δεωωε.

We notice, in the above example, that, for finding a stable position of equilibrium, it

has been necessary to solve completely the initial value problem, hence to determine the

co-ordinates of the representative point

P ,

00 000 0

12 12

( ; , ,..., , , ,..., ), 1,2,...,

qqtqq qqq qj s 

(23.1.3)

as functions of the initial conditions and of time (in the particular case

1s =

); it is

possible (the most times) to be not very simple to do it. Thus, it is worth to find a

stability criterion for the position of the equilibrium which does not need the integration

of the differential equation (or of the system of differential equations) of motion of the

discrete mechanical system.

Stability and Vibrations

509

It is necessary to make some observations before dealing with such a criterion. If

only the trajectory of the representative point

P remains in the neighbourhood of a

position of equilibrium, its velocities, in a perturbed motion, differing very much from

those in the non-perturbed motion, we say that the motion is orbitally stable.

Obviously, a stable motion is orbitally stable too; but an orbital stable motion is not – in

general – stable.

The notion of stability, introduced for a position of equilibrium, has been extended

also to the motion of a discrete mechanical system

S . If, to very small perturbations of

the initial conditions corresponds a motion which – from the point of view of the

trajectory of the representative point, as well as of its generalized velocities – remains

always in the neighbourhood of the non-perturbed motion, then the considered motion

is stable; otherwise, it is instable.

More precisely, let us denote by

( ), 1,2,...,2

xt i s=



, the state of the representative

point



in the phase space

Γ (the generalized co-ordinates and the generalized

momenta, hence the canonical co-ordinates), in a non-perturbed motion the discrete

mechanical system

S ; let be, as well, ( ), 1,2,...,2

xt i s= , the corresponding

variables in a perturbed motion. If, an arbitrary

> 0ε being given, one can determine

(, ) 0tδδε so that, for any ≥

tt, the inequalities

−<=( ) ( ) , 1,2,...,2

xt xt i sε



(23.1.4)

take place, assuming that at the initial moment

tt= hold the inequalities

−<=

( ) ( ) , 1,2,...,2

xt xt i sδ



(23.1.4')

then the motion of the representative point

P (hence, of the discrete mechanical system

S ) is stable.

We can express the above condition of stability also in the form

[]

−<

∑

() ()

xt xt r



(23.1.5)

where

r is an as small as we wish real number; no one of the absolute values

| ( ) ( ) |, 1,2,...,2

xt xt i s−=



, can be greater than r . If ()

xtare continuous

functions and if

r is sufficiently small, then the representative point

will be as close

as we wish from the representative point



, in the interior of the hypersphere

S ,

[]

() ()

xt xt r

−=

∑



(23.1.5')

of centre



and radius r . Indeed, we can pass from one definition to another one,

observing that the point



is at the moment

t in the interior of a hypersphere S

, of

radius

δ , and that, in the perturbed state, at the moment t , the point P is in the

interior of a hypersphere

, of radius ε , concentric with S

MECHANICAL SYSTEMS, CLASSICAL MODELS

510

A representative point

P , which verifies the inequality

[]

() ()

xt xt r

−>

∑



(23.1.5'')

is exterior to the hypersphere

S ; hence, there exists at least an absolute value

| ( ) ( ) |, 1,2,...,2

xt xt i s−=



, which is greater than the value r . Hence, if r is

sufficiently great, the condition (23.1.5'') corresponds to instable motion.

Let

12 2

( , ,..., ; ), 1,2,...,2

Xxx x t i s

(23.1.6)

be a system of

2s differential equations of first order, e.g., Hamilton’s canonical

equations; we assume that the gives functions

, 1,2,...,2

Xi s= , satisfy the conditions

of the Cauchy-Lipschitz theorem of existence and uniqueness (see Sect. 19.1.1.4). We

make firstly a study of the stability of a certain solution

( ) 0, 1,2,...,2

xt i s==



, of

this system, which – obviously – verifies the relations

()

12 2

d()

( ), ( ),..., ( ); , 1,2,...,2

Xxtxt x tti s



 

(23.1.6')

Subtracting the differential equations (23.1.6), (23.1.6') one from the other and

making the change of functions

( ) ( ) ( ), 1,2,...,2

iii

xt xt yt i s=+ =



, we may write

()

[]

11 22 2 2

12 2

( ), ( ),..., ( );

( ), ( ),..., ( ); , 1,2,...,2 ,

Xy xty xt y x tt

xtxt x tt i s

=+ + +

−=

 

(23.1.7)

obtaining thus the system of differential equations of the perturbed motions, called so

by Alexandr Mikhailovich Lyapunov; this denomination is due to the fact the variables

y are equal to the perturbations ( ) ( ), 1,2,...,2

xt xt i s−=



. This system admits –

obviously – the solutions

0, 1,2,...,2

yi s== , which can be considered as

corresponding to a configuration of equilibrium. Thus, the passing from the system

(23.1.6) to the system (23.1.7) means the passing from the study of the stability of

motion to the study of the stability of a configuration of equilibrium; hence, we will

begin with the study of the position of equilibrium of the representative point

P .

Without any loss of generality, we can return to the system of equations (23.1.6),

assuming that the solutions

12 2

... 0

xx x=== = are verified; hence, we study the

stability of these solutions.

If, an arbitrary

0ε > being given, one can determine

(, ) 0tδδε=>, so that, for

any

tt> , the inequality

22 2

12 2

() () () ... ()

txtxt xtρε=+++<

(23.1.8)

Stability and Vibrations

511

takes place, assuming that, at the moment

tt= , holds the inequality (

()

xt x= ,

1,2,...,2is= )

() () ( )

22 2

00 0

12 2

...

xx xρδ=+++<,

(23.1.8')

then the trivial solution

0, 1,2,...,2

xi s== is stable in Lyapunov’s sense.

Otherwise, the motion is instable. The Cauchy–Lipschitz theorem ensures the existence

and the uniqueness of the solution and, as well, of the continuous dependence of it at

the initial data in the vicinity or the moment

tt= . To introduce the notion of stability

in Lyapunov’s sense, it is necessary to can prolong the non-perturbed solutions, as well

as all the perturbed solutions for any

tt> . Hence, the stability problem is the

problem of its continuous dependence on the initial data on an infinite interval of time.

If the above solution is stable in Lyapunov’s sense and if there exists

0δ > , so that the

condition (23.1.8') be verified, the condition

22 2

12 2

lim ( ) lim ( ) ( ) ... ( ) 0

txtxtxtρ

→∞ →∞

=+++=

(23.1.8'')

being also involved, then we say that the solution is asymptotically stable (or

completely stable); hence, the point

P of the perturbed position tends to the position of

stable equilibrium in an infinite time. The domain in the space

Γ for which any

motion which starts from a point of it is asymptotically stable is called domain of

attraction of the point

0, 1,2,...,2

xi s== ; if this domain is just the whole space,

then the corresponding solution is called globally stable.

If the functions

12 2

( , ,..., ; ), 1,2,...,2

XXxx xti s==, depend explicitly on

time, then the system of differential equations (23.1.6) is non-autonomous; otherwise,

hence if

12 2

( , ,..., ), 1,2,...,2

XXxx x i s==, the system is called autonomous or

dynamical.

Let us consider now an autonomous system and let us suppose that the solutions

( ), 1,2,...,2

xt i s= , correspond to periodical motions; the trajectory C in the phase

space will be closed. Let be a point

′

∈ and a point P is the neighbourhood of this

curve; by definition, the distance from the point

P to the curve C is given by

d( , ) inf {d( , ), }PC PP P C

′′

=∈.

If, being given

0ε >

arbitrary, there exists

(, ) 0tδδε=>, so that any solution

12 2

( ), ( ),..., ( )

xtxt x t which passes through the point

00 0

12 2

( , ,..., )

Px x x of

Γ at

the moment

tt=

and fulfils the condition

d( , )PC δ<

(23.1.9)

has the property