Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

482

We can thus write

=== == =

∂

⋅δ = ⋅ δ = ⋅ δ = δ

∂∂

∑∑∑ ∑∑ ∑

ar aB a

111 11 1

nnh hn h

ii i ii ij j ii j

iij ji j

mm mπππ

ππ 

where we have introduced the acceleration energy (22.3.1). As well,

=== =

⋅δ = ⋅ δ = δ

∑∑∑ ∑

Fr FB

111 1

nnh h

ii iijj jj

iij j

Qππ

with the quasi-forces

=⋅ =

∑

, 1,2,...,

jiij

Qjh.

(22.3.9)

The theorem of virtual work, written in the form (18.2.27), leads to

∂

⎛⎞

−δ=

⎜⎟

∂

⎝⎠

∑

Q π

π

;

the variations

π being independent, there result the Gibbs–Appell equations

∂

, 1,2,...,

Qj h

π

(22.3.10)

the number of which is equal to the number of kinetic degrees of freedom. We have

thus

h differential equations of second order, to which we associate m non-holonomic

constraint relations (22.1.19), (22.1.20), for the

s unknowns , 1,2,...,

qk s= ; thus,

the number

+=hms of equations will be equal to the number of unknowns.

In particular, we can take as quasi-co-ordinates just the independent generalized

co-ordinates. If the mechanical system is holonomic (

0, mhs==), then the

Gibbs-Appell equations become

∂

, 1,2,...,

Qj s

q

(22.3.11)

obtaining a system of equations equivalent to Lagrange’s equations.

22.3.2 Applications

We present in what follows some applications of the Gibbs–Appell equations to the

motion of a rigid solid with a fixed point, as well as to the motion of a disc on a

horizontal plane or to the motion of a sphere on an inclined plane or on a horizontal

plane in uniform motion.

Dynamics of Non-holonomic Mechanical Systems

483

22.3.2.1 Motion of a Rigid Solid with a Fixed Point

Let be a rigid solid S , which is rotating with the angular velocity ω about the

fixed point

′

≡OO

, with respect to an inertial frame of reference

′

R and to a

non-inertial frame

R , which is rotating about the fixed frame with the angular

velocity

Ω . The velocity of a point P of the rigid solid with respect to the inertial

frame is given by

′

=×

vrω , where r is the position vector with respect to both

frames of reference. In this case, the acceleration

′

a is obtained in the form

() ()

()

[]

()

∂

′

=×+××=×+×−×+××

∂

=× × −×+×× +× ×

ar rr r r

rr r r



ωΩωωωωΩ Ωω

ωω ωω Ω Ωω

where we have taken into account the relation (A.2.37), which is linking the derivative

with respect to the fixed frame to the derivative with respect to the movable one; using

the relations (2.1.49), (2.1.50') too, we obtain, finally,

()

′

=⋅ − −× =+×arrr



ωωω

χχ

ωΩω.

(22.3.12)

Projecting on the axes of the frame of reference

R , it results

()

()()

()

()()

()

′

=− + + − + +

′

=+−++−

′

=−++−+

123112 213 3

212 131223 3

331 132 2123

axxx

χχ

ω ω ωω ωω

χχ

ωω ω ω ωω

χχ

ωω ωω ω ω

(22.3.12')

with

=+ −

12332

23113

31221

;

ωΩωΩω



(22.3.12'')

The acceleration energy is thus given by

()

′ ′′′

=++

∫∫∫

222

123

()d

S aaa Vμ ,

where

r()μ is the density and V is the volume of the solid. We can choose the

quasi-co-ordinates so that

, 1,2,3

kπω== . Because we are interested only in the

dependence on

π , hence on



, we hold back in the expression of

′

a only the terms

()()

()

()()

[]

′

=− +−

++ − + − −

222

3322

1122133

32 2323

23 12 13 12 3 23

22 ;

axx

xx xx xx

χχχχ

ωω ωω

χχ χχχχ

ωω ωω ω

MECHANICAL SYSTEMS, CLASSICAL MODELS

484

we proceed analogically for

′′

,aa. Taking into account the definitions given in Sect.

3.1.2.1 for the moments of inertia, we can calculate the part

S of

′

, which is of

interest in what follows. We can assume, without any loss of generality, that the axes of

the frame of reference are rigidly linked to the rigid solid

S ; in this case, =Ωω, so

that

, 1,2,3

ωπ== =



. If, for the sake of simplicity, we choose the principal

axes of inertia of the rigid solid at the fixed point

O as axes , 1,2,3

Ox k = , we

obtain

()

() ()

′

=+++−

+− + −

222

11 22 33 3 2 123

13231 21312

SIII II

II II

πππ πππ

     

     

(22.3.13)

where we have put in evidence the principal moments of inertia.

Observing that the work of the moments of the given forces with respect to the given

pole is expressed in the form

⋅= =

∑∑

ddd

jj j j

tMtMωπω ,

it results

==,1,2,3

QMj . In this case, the Gibb–Appell equations (22.3.11) lead

to Euler’s equations (15.1.11'').

In the particular case in which the ellipsoid of inertia of the rigid solid is of rotation,

we can choose as axis of inertia just the

Ox -axis. In this case

1122

, ΩωΩω==, but

≠

Ωω; all the centrifugal moments of inertia vanish and ==≠

12 3

IIJI. We

obtain

() ()

=+ − =− − =

122

123 3 213 3 3

χχχ

πππΩ πππΩ π       ,

so that

()

[]

()( )

′

=+++− −

1 2 33 33 3 12 21

SJ I IJππ π π Ωππππ

        ,

(22.3.14)

where we have neglected the terms which do not contain quasi-accelerations. The

Gibbs-Appell equations will be of the form

()

+− =

−− =

133 32

233 31

JIJ M

ππωπ

  



(22.3.15)

where

, 1,2,3

Mj= , are the components of the resultant moment M

with respect

to the fixed pole.

Dynamics of Non-holonomic Mechanical Systems

485

22.3.2.2 Motion of a Heavy Circular Disc on a Horizontal Plane

Using the Gibbs–Appell equations, we take again the problem of motion of a heavy

circular disc, of radius

R and mass M , on a horizontal plane, problem considered in

Sect. 22.2.3.2 in quasi-co-ordinates (see Fig. 22.1). To calculate the acceleration

energy, we use the Theorem 22.3.1. We notice that the acceleration energy with respect

to the pole

O is given by (22.3.14); to calculate the acceleration energy of the mass

centre

O . we calculate firstly the acceleration

′

of this point.

The velocity of the contact point

I must vanish; hence,

′′

=+×=

OI 0

wherefrom we get the components of the velocity

′

in the form

′′ ′

==− =

12 3

0, ,

OO O

vvRvRωω.

The acceleration will be given by

′′ ′

=∂ ∂ + ×

av v/

OO O

t Ω , so that

(

1122

, ΩωΩω==

)

()

()()

′′ ′

=+ =−+ =−

233 312 213

12 3

OO O

aR a R aRωΩω ωωω ωωω



;

taking into account

, 1,2,3

jωπ== , we obtain

()

′

=++ −

⎡⎤

⎣⎦

2222

23 12332

aRππ πππππ       ,

(22.3.16)

where we have neglected the terms which do not contain the characteristics, The

acceleration energy of the disc is thus given by

()( )

()()()

′

=++ ++

⎡⎤

⎣⎦

+−+−−

222 22

123 32 33 3 12 21

SJJMR IMR

MR I J

ππ π

πππ ππ π Ω ππ ππ

  

    

(22.3.17)

The work of the weight will be

=−

dcosdQq MgR θθ, where we have used the

notations in Sect. 22.2.3.2.

In the considered case we have = 5s generalized co-ordinates, linked by = 2m

non-holonomic relations; hence,

=− =−=52 3hsm . The Gibbs–Appell equations

read

()

()( )

()

+− =

+−+ +=−

++ =

133 32

23 13 31

3312

cos ,

JIJ

JMR I MR J MgR

IMR MR

ππΩπ

πππΩπθ

πππ

  

   

  

(22.3.18)

Observing that

32 3 32

, ψθϕ ψθ

′′

=++ =+

 

ii i iiωΩ, of components (along the

axes of the frame of reference

R ),

123

sin , , cosω ψ θω θω ψ θ ϕ=− = = +



 ,

MECHANICAL SYSTEMS, CLASSICAL MODELS

486

the system of differential equations (22.3.18) becomes (

, 1,2,3

kπω== )

()

()( )

()

22 2

sin 2 cos ,

sin sin cos cos ,

sin ,

JMR I MR J MgR

IMR MR

ψθ ψθθ ωθ

θωψθψθθθ

ωψθθ

+++ − =−

   

  





(22.3.18')

with the unknown functions

(), ()ttψψ θθ== and =

()tωω .

The first equation (22.3.18') takes the form

()

sin sin

ψθωθθ



(22.3.18'')

To obtain the differential equations which define

ω and ψ



as functions of

, we

write the third equation (22.3.18') and the equation (22.3.18'') in the form

()

⎛⎞

++= −+=

⎡⎤

⎜⎟

⎣⎦

⎝⎠

10,10

uIu

ψψω



where we have used the change of variable

= cosu θ . Eliminating the unknown

functions

ω and ψ



, respectively, we obtain

() ()

⎡⎤

−−=−−=

⎢⎥

⎣⎦

10,10

λω λζ

(22.3.19)

with the notation

()

=− =

IMR

ζψλ



(22.3.19')

The disc being homogeneous, we have

2IJ, so that

2MR

IMR

(22.3.19'')

If the disc is whole, then =

/2IMR and it results = 4/3λ , while if the disc is

reduced to its circumference we have

IMR and = 1λ ; analogically, one can

consider also the case of a circular annulus. We mention that the first equation (22.3.19) is

of Legendre type, which defines the hypergeometric functions (see Sect. 22.2.3.2 too).

The theorem of uniqueness allows to state that the system (22.3.18') has the solution

== = =

0, , , const

ψθ ωωω



(22.3.20)

Dynamics of Non-holonomic Mechanical Systems

487

if this one corresponds to the initial conditions; in this case, the point of contact

describes a straight line (

constψ

), the plane of the disc remaining normal to the

fixed plane (

= /2θπ), while the rotation of the disc is uniform

(

=+ =

,consttϕω ωω ). If we put =+/2θπ ε, =ψξ



and =+

ωωη in the

equations (22.3.18') and if we linearize the system thus obtained, then we can write

()( )

=+++ ==

,,0JI JMR IMR MgRξωε ε ωξ εη







wherefrom

()( )

+++ − =

⎡⎤

⎣⎦

222

0J J MR I I MR JMgRεωε

 

;

()

II MR JMgRω , then the solution is stable, in a first approximation.

22.3.2.3 Motion of a Heavy Sphere on an Inclined Plane

Let be now the case of a heavy homogeneous sphere, of radius R and mass M ,

which has a motion of rolling without sliding on a plane inclined by an angle α with

respect to a horizontal plane. We choose, in the inclined plane, the

′′

Ox -axis along the

direction of maximal inclination and the

′′

Ox -axis parallel to the horizontal plane; the

Fig. 22.17 Motion of a heavy sphere on an inclined plane

′′

Ox -axis is normal to this plane (Fig. 22.17). A point

of the sphere will be

specified by the co-ordinates

′′′

123

,,xxx R of the centre

of the sphere and by

Euler’s angles

,ψθ and ϕ . Because the sphere rolls without sliding, it results that the

velocity of the contact point

must vanish, so that

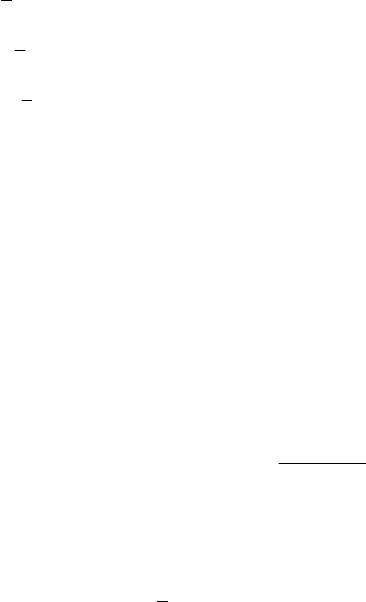
MECHANICAL SYSTEMS, CLASSICAL MODELS

488

′′

=+×=

CI 0

ω ,

where ω is the rotation velocity of the movable frame, rigidly linked to the sphere.

Projecting on the axes of the fixed frame of reference, we obtain the non-holonomic

constraint relations

′′ ′′

−= +=

12 21

0, 0xR xRωω;

(22.3.21)

we can thus define the quasi-co-ordinates

123

,,πππ by the relations (5.2.35') in the

form

′

== +

′

==− +

′

== +

sin sin cos ,

sin cos sin ,

cos .

πωϕθψθψ

πω ϕθψθψ

πωϕθψ













(22.3.22)

The acceleration energy is given by

()( )

()()

′′ ′′′

=++++

⎡⎤

⎣⎦

′′ ′

=+ ++

⎡⎤

⎣⎦

=+ ++

⎡⎤

⎣⎦

12 1 2 3

12 3

22 2 2 2

222 2

12 3

SMxxI

IMR I

ωωω

ωω ω

ππ π

 



 

  

(22.3.23)

where we took into account (22.2.21), (22.2.22) and where

I is the moment of inertia of

the sphere with respect to one of the diameters. The work of the own weight is given by

′′

=− =− =

21 111

sin d sin d sin d dMg x Mg t MgR Qαωα αππ,

because

′

d0x .

The Gibbs–Appell equations read

()

+=− ==

123

sin , 0, 0IMR MgRπαππ  

;

(22.3.24)

it results, by integration,

=− + = = =

112233

sin

,,,

MgR

Kt C C C K

IMR

πππ

 ,

(22.3.24')

where

123

,,CCC are arbitrary constants. The co-ordinates of the point P of the sphere

will be thus given by the equations

′′′ ′

=+ = ++

12 22 1 1

xCRtCx KRtCRtC

(22.3.25)

Dynamics of Non-holonomic Mechanical Systems

489

()

[]

()

[]

=+ + +

=− + +

12 3

sin cos cot

cos sin ,

sin cos cosec .

Kt C C C

Kt C C

ψψψθ

θψψ

ϕψψθ



(22.3.25')

If the sphere moves on a horizontal plane (

= 0α ), then it results = 0K and the

mass centre has a uniform and rectilinear motion; in the case in which

≠ 0α , the mass

centre is moving along a parabola of axis parallel to the

′′

Ox -axis or along the

direction of this axis if the initial velocity (for

= 0t ) vanishes ( ==

0CC ) or is

along a parallel to it (

0C ).

22.3.2.4 Motion of a Sphere on a Horizontal Plane in Uniform Rotation

Let us consider the motion of a homogeneous sphere, of radius R and mass

, on

a horizontal plane

′′′

Oxx , which has a uniform rotation of angular velocity

about

the vertical axis

′′

Ox ; the axes

′′

Ox and

′′

Ox are fixed in the plane of rotation. The

problem has been previously studied in Sect. 22.2.3.3 (see Fig. 22.13). The constraint

relations (22.2.65) can be written in the form

′′′′ ′′

=− =−+

1222 11

,xR xx R xωΩ ωΩ,

(22.3.26)

′′

,xx and

′

xR being the co-ordinates of the centre C of the sphere; there result

the acceleration

() ()

′′ ′′′ ′ ′′

=+ − =−+ −

12 112 1 22

,xR R xx R R xωΩωΩ ωΩωΩ 



the acceleration of the centre

being given by

()

()()

[

]

222222

12 1 2 21 1 12 2

axxR R R x R xωω ΩωωΩ ωωΩ

′′′ ′′ ′′ ′′′ ′

=+= + + − − − 

  

where we have ignored the terms which do not contain derivatives of second order of

the quasi-co-ordinates, specified by

1122

, ωπωπ

′′

==.

The acceleration energy is given by ( =

IMi, where I is the central axial moment

of inertia,

i is the corresponding gyration radius and

′

ωπ )

()()( ){

()()

[]

}

′

=+++= ++

⎡⎤

⎣⎦

′′

++ − − −

222 2 2 22 2 2

123 12

3211122

SMai MRi

iRRx Rx

πππ ππ

πΩππΩππΩ

    

    

(22.3.27)

observing that

0, 1,2, 3

Qj== , the Gibbs–Appell equations relative to the

quasi-accelerations

π lead to the equations (22.2.70), (22.2.70'), studied in Sect.

22.2.3.3.

If we use the quasi-accelerations

12 3 3

, , xxωπ

′′′

=  



and notice that

MECHANICAL SYSTEMS, CLASSICAL MODELS

490

() ()

′′′′′′

=− − =− +

121212

,xx xx

ωΩωΩ   



then the acceleration energy is written in the form

()

⎧

⎡⎤ ⎫

′′ ′′′′

=+ +++ −

⎨

⎬

⎢⎥

⎩⎣ ⎦ ⎭

2222

12 3 1221

SM xx i xxxx

πΩ      

(22.3.27')

where, as well, we maintained only the terms which contain quasi-accelerations.

Assuming that upon the sphere acts a system of arbitrary given forces, the torsor of

which at the centre

C is given by R and M , of the components ,, 1,2,3

RM j= ,

and writing the constraint relations (22.3.26) by means of the virtual displacements in

the form (

, 1,2,3

ωπ

′



)

′′

δ=δ δ=−δ

122 1

,xR x Rππ,

(22.3.26')

we obtain the virtual work

′′′

δ=⋅δ+⋅δ=δ+δ+δ+δ+δ

⎛⎞⎛⎞

′′

=+ δ+− δ+δ

⎜⎟⎜⎟

⎝⎠⎝⎠

Rr M

11 22 11 22 3 3

112233

;

WRxRxMMM

RxRxM

πππ

hence,

***

112 221 3 3

/, /, QRMRQRMRQM=+ =− =.

The Gibbs–Appell equations (22.3.10) lead to

()

′′

++ = +

⎡⎤

⎣⎦

′′

+− = −

⎡⎤

⎣⎦

22 2

12 12

22 2

21 21

MR ix ix RRR M

Mi M

Ω



(22.3.28)

If the sphere is subjected only to the action of the own weight, then

0, 1,2, 3

RM j== = , and we find again the equations (22.2.70), (22.2.72).

Assuming now that the plane which is rotating is inclined by the angle

α with respect

to the horizontal plane, we have

sinRMgα , the other components of the torsor

vanishing.

Denoting

i, i 1zx x=+ =−, we can write the system (22.3.28) in the form

−= = =

22 22

sin

ii, ,

iRg

zkzkK K

Ri Ri

Ωα



(22.3.29)

the solution being given by

=+ −

zC Ce t

;

(22.3.29')

Dynamics of Non-holonomic Mechanical Systems

491

the complex constants

,CC are determined by initial conditions.

22.4 Other Problems on the Dynamics of Non-holonomic

Mechanical Systems

We will consider also other aspects of interest concerning non-holonomic problems;

let us thus mention the collisions – phenomena with discontinuity – as well as the

obtaining of first integrals for the equations of motion.

22.4.1 Collisions

The phenomenon of collision is due to the apparition of some percussive forces or to

the sudden application of some non-holonomic constraints; in what follows, we present

the discontinuous phenomena which put in evidence both cases.

22.4.1.1 Basic Equations

From the very beginning, we notice that the non-holonomy does not introduce

something essential from the point of view of the percussions, defined by the same

formula (10.1.40) in the form

′′

′

′′ ′

−→+

∫

lim ( )d

tt,

(22.4.1)

where

F is a percussive force, the limit being considered in the sense of the theory of

distributions in the collision interval

[, ], | | , 0tt t t εε

′′′ ′′ ′

−< > arbitrary, which

contains only one moment of discontinuity

t . The corresponding general theorems are

given in Sect. 10.1.2.3, and the general study for a single particle is presented in Sect.

13.1.1.2.

Corresponding to the theorem of momentum 13.1.2, stated in the space

E , we can

pass to the Theorem 18.3.1, stated in the space of configurations

Λ , according to

which the jump of the generalized momentum of a discrete mechanical system

subjected to constraints, corresponding to a generalized co-ordinate, at a moment of

discontinuity is equal to the sum of the given and constraint generalized percussions,

corresponding to the same co-ordinate and which act upon this system at that moment.

We assume that, in the interval of percussion, both the generalized co-ordinates

, ,..., , ,...,

qq qq q of a representative point P and the kinematic characteristics

, , 1,2,..., , 1,2,...,

kj k

aa k mj h== of the constraint relations (22.1.1) or (22.1.1')

remain constant. As in case of the Chaplygin system (see Sect. 22.2.4.1), we assume

that the generalized velocities corresponding to the first

h co-ordinates can be

considered to be independent and that the other

−sh co-ordinates do not intervene in

the coefficients

,,0

, , 1,2,..., , 1,2,...,

hkj hk

cc k shj h

=−=, of the non-holonomic

constraint relations, written in the form (the matrix

[]

a is of rank h )

+++

=+=−

∑

,,0

, 1,2,...,

hk hkj hk

qcqck sh ;

(22.4.2)