Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

462

this point with respect to the fixed frame, given by

222

(cos)(sin)

vxl xlθθ θθ

′′ ′

=− +−



, replacing the moment of inertia

Mi by

−

()Mi l , corresponding to Koenig’s theorem; one obtains thus

()

′′′′′

=+− ++

⎡⎤

⎣⎦

22 22

12 1 2

2cos sin

TMxxlx x iθθ θθ



   .

(22.2.77')

We denote by

′

T and

′

T the kinetic energies of the two wheels; we can write

()

′′

=+++v

2222

2112233

Tm I I Iωωω,

where

I are the principal moments of inertia of the respective wheel with respect to its

centre, while

, 1,2,3

kω = , are the corresponding angular velocities, along the

directions of the axes of the movable frame; we notice that

III,

I corresponding to the axis

Cx, while

122 3

, 0, ωϕω ω θ===



. Because

112 2

(sin)(cos)

xa xaθθ θθ

′′ ′′ ′

=− ++



vii

, it results

()

{}

′′′ ′′

=++− −++

⎡⎤

⎣⎦

2222 2 2

212 12 12

2sin cos

Tmxxa ax x IIθθ θ θθϕ

 

   ;

(22.2.78)

analogically

()

{}

′′′ ′′

=+++ −++

⎡⎤

⎣⎦

2222 2 2

112 12 11

2sin cos

Tmxxa ax x IIθθ θ θθϕ

 

   .

(22.2.78')

Finally, the kinetic energy

′′′′

=++

TTTT is expressed in the form

() ()

()

′′′′′

=++++

⎡⎤

⎣⎦

′′

=+ = + +

22 2 22

12 112

2, 2 ,

TMxxII

MMmI Ima Mi

θϕϕ



 

(22.2.79)

≡CO

, and in the form

() ()

()

22 2 22

12 112 1 2

2cos sin

TMxxII Ix xθϕϕ θθ θ

′′′′′ ′ ′

=++++− +

⎡⎤

⎣⎦



   

(22.2.79')

in the general case.

Writing Lagrange’s equations, one must not take into account the constraint relation

(22.2.76) in the expression of the kinetic energy (22.2.79'); it can be used only after

writing these equations. As well, we notice that the own weight (the only force which is

applied upon the mechanical system) does not produce work; hence, the generalized

forces vanish. We can thus write the first integral of mechanical energy in the form

(valid also if the centre of mass is not at

O )

Dynamics of Non-holonomic Mechanical Systems

463

() ()

′′ ′ ′

+++ +=

22 2 22

12 112

2Mx x I I hθϕϕ



 

(22.2.80)

where

h is the energy constant.

Using the general form (22.2.14) of the constraint relations, the relations (22.2.73'),

(22.2.76) allow to write

== =− ==−=

== =− =−==−

== = ===

10 11 12 13 14 15

20 21 22 23 24 25

30 31 32 33 34 35

0, sin , cos , , , 0,

0, sin , cos , , 0, ,

0, cos , sin , 0, 0, 0.

aa a aaaRa

aa a aaaaR

aa a aaa

θθ

Limiting ourselves to the case

≡CO ( = 0l ), Lagrange’s equations with

multipliers (22.2.13) are written in the form

() ()

()

′′ ′′

=+ + =−+ +

′

= − =− =−

112 3 2 12 3

12 11 112 2

sin cos , cos sin ,

,,.

Mx Mx

IaIRIR

λλ θλ θ λλ θλ θ

θλλ ϕ λ ϕ λ

 



 

(22.2.81)

Eliminating Lagrange’s multipliers

,λλ between the last three equations, we get

()

′

=− −

11 2

θϕϕ



  ,

wherefrom

()( )

′′

=− − + +

11 2 1 2

II ICtC

θϕϕ ,

(22.2.82)

,CC being two integration constants. From (22.2.75), (22.2.82) it results

−

=+ = = +

−

−= + =+

′

() , , ,

CCk

tt k

aK a K

Ck I

aRa

RK aRI

θωψω ψ

ϕϕ ω

(22.2.83)

Eliminating the multipliers

λ between the first two equations (22.2.81) and then the

multipliers

,λλ, by means of the last two equations of Lagrange, we can write

()()

′′ ′

−=+=−−

12 12 12

sin cos

Mx x

θθλλ ϕϕ    ;

we notice that

()

′′ ′′

−= − =−+=+

12 12 1 2

sin cos sin cos

x x x x aR aR

θθ θθθϕθϕ

 

     

MECHANICAL SYSTEMS, CLASSICAL MODELS

464

where we took into account the constraint relations (22.2.75), (22.2.76). Observing that

= 0θ



, it results ==

0ϕϕ  , so that

() ()

=+ =+

=+ =−

=+ − =− −

111222

() , () ,

tt tt

ϕωψϕωψ

ωω ωωω ω

ψψ ψ ψψ ψ

(22.2.83')

the angles

,,θϕ ϕ depending thus on the angular velocities ω and

ω and on the

non-dimensional constants

,,k ψψ , which are determined by initial conditions. In this

case, the relation (22.2.74) can be written in the form

′′

−=

sin cosxx Rθθω ;

taking into account the relation (22.2.76) too, we obtain also the co-ordinates of the

point

() ()

′′ ′′

=− + =− +

11 22

cos , sin ,xx R t xx R t

ωω

ωψ ωψ

ωω

(22.2.83'')

where the constants

′′

,xx

are specified by the initial conditions too.

Lagrange’s multipliers

== =

12 3

0, Rλλ λ ωω

(22.2.84)

and the generalized constraint forces

() ()

=+=+

===

cos , sin ,

RR t RR t

RRR

ωω ω ψ ωω ω ψ

(22.2.84')

are determined by the equations (22.2.81).

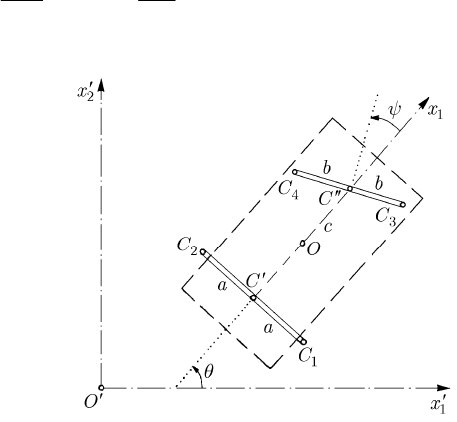
22.2.3.5 Motion of the Four-Wheeled Carriage

Let be a carriage with four wheels, of centres

123

,,CCC

and

, which are rotating

independently by the angles

123

,,ϕϕϕ and

ϕ , respectively; we denote by

′

and

′′

the middles of the two axles and take the pole

of the movable frame of reference at the

mass centre, considered to be situated on the straight line

′′′

, which is taken as

-axis and is parallel to the plane

′′′

Oxx . The

-axis makes the angle

with the

′′

Ox -axis, while the

-axis is parallel to the

′′

Ox -axis. The two axes of the wheels are

of lengths

and

, respectively, and make the angle

between them (Fig. 22.15). The

wheels of centres

and

are of radii

′

and masses

′

, while the wheels

and

are of radii

′′

and masses

′′

; the mass of the carriage without wheels is

. Let be

′′

,xx the co-ordinates of the point

′′

; in this case, the co-ordinates of the points

′

and

Dynamics of Non-holonomic Mechanical Systems

465

will be

cos , sinxl xlθθ

′′

−− and

′

−

cosxcθ ,

′

−

sinxcθ , respectively,

where

′′′

lCC and

′′

cOC. We can use thus eight generalized co-ordinates

′′

,xx,

,θψ

123

,,ϕϕϕ and

ϕ .

Fig. 22.15 Motion of a four-wheeled carriage

As in the case of the two-wheeled carriage, we can write the constraint relation (we

notice that the angle

has another significance that in the preceding case)

() ()

′′

+− +=

sin cos 0xxθψ θψ

(22.2.85)

for the front wheels. Passing from the co-ordinates of the point

′′

to the co-ordinates

of the point

′

, one obtains the constraint relation

′′

−+=

sin cos 0xxlθθθ





(22.2.85')

for the backwheels. Analogically, equating to zero the velocities of the contact points of

the wheels of centres

and

, respectively, we obtain

′′ ′

+++=

′′ ′

+−−=

12 1

cos sin 0,

cos sin 0;

xxaR

θθθϕ



 



 

(22.2.86)

by equating to zero the velocities of the contact points of the wheels of centres

C and

C , respectively, we can also write

() ()

()

() ()

()

′′ ′′

++ ++ ++ =

′′ ′′

++ +− +− =

12 3

12 4

cos sin 0,

cos sin 0.

xxbR

θψ θψ θψ ϕ



 



 

(22.2.86')

We have obtained six non-holonomic constraint relations, the mechanical system being

thus non-holonomic and scleronomic with two degrees of freedom.

MECHANICAL SYSTEMS, CLASSICAL MODELS

466

The kinetic energy of the axles and of the carriage which is supported by them is of

the form

′′′′′′

=++++

1234

TTTTTT, where, by a calculation analogous to that of

the preceding subsection, we have

()

()()

()

()()

′′′ ′′

=+++ − +

⎡⎤

⎣⎦

⎡

′′′ ′

=++−+

⎣

′′ ′′

++++

⎤

⎦

⎡

′′′ ′

=++−+

⎣

′

−

2222 2

12 1 2 3

11 2

12 1

21 2

2sin cos ,

sin cos

2cos sin ,

sin cos

2cos

TMxxc cx x I

Tmxl xl a

ax x J I

Tmxl xl a

θθ θ θ θ

θθ θθ θ

θθ θ θϕ

θθ θθ θ

θθ

 

  





 







()

′′′

+++

⎤

⎦

sin ,

xJIθθϕ





{

()

() ()

]

}

[

()

{

()

() ()

]

}

[

()

′′′′′

=+++

′′ ′′′′

++ ++ + + ++

′′′′′

=+++

′′ ′′′′

−+ ++ + + ++

222

312

12 3

222

412

12 4

2cos sin ,

2cos sin ;

Tmxxb

bx x J I

Tmxxb

bx x J I

θψ

θψ θψ θψ θψ ϕ

θψ

θψ θψ θψ θψ ϕ



 

 



 

 

we have denoted by

I the moment of inertia of the carriage without wheels with

respect to the

-axis, by

′

and

′′

the principal moments of inertia of the wheels

C and

C , respectively, with respect to their axes and by

′

and

′′

the other

principal moments of inertia of the same wheels. Thus, we obtain

()

()( )

()

()()

′′′′ ′′ ′

=+++ ++

′′ ′′ ′ ′′

++ ++ ++ +

⎡⎤

⎣⎦

22 2

12 1 2

22222

12 34

2sincos

TMxx Mcmlx x J

ml J I I

θθ θθ

θψ ϕ ϕ ϕ ϕ



  



 

(22.2.87)

where

()

()()

′′′′ ′ ′

=+ + = + + + +

222

MM mmJ McI mla J

(22.2.87')

represent the total mass of the carriage and a quantity of the nature of a moment of

inertia, respectively.

One can thus obtain the eight Lagrange’s equations with multipliers, to which one

associates the six constraint relations; hence, the eight generalized co-ordinates and the

six Lagrange’s multipliers can be determined.

Dynamics of Non-holonomic Mechanical Systems

467

22.2.4 Other Equations of Motion

In the following, we put in evidence other equations of motion, corresponding to the

non-holonomic mechanical system, i.e.: Chaplygin’s equations, Voronets’s equations,

Volterra’s equations and Maggi’s equations; as well, we obtain the canonical form of

the equations of motion (Hamilton’s equations in quasi-co-ordinates) too (Chaplygin,

S.A, 1954).

22.2.4.1 Chaplygin’s Systems. Chaplygin’s Equations

S. A. Chaplygin noticed that, in the case of many non-holonomic conservative

mechanical systems, the generalized co-ordinates

, ,..., , ,...,

qq qq q can be

chosen so that the generalized velocities corresponding to the first

h co-ordinates be

considered independent; the other

−sh co-ordinates do not intervene, neither in the

coefficients

+ ,hkj

c of the catastatic constraint relations (22.1.1') (where we make

a ), written in the form (the matrix

⎡

⎤

⎣

⎦

a is of rank h )

==−

∑

, 1,2,...,

hk hkj

qcqk sh ,

(22.2.88)

nor in the expression of the Lagrangian

L , written without taking into account these

constraint relations (so that

/ 0, 0, 1,2,...,

hk hk

Tq Q k sh

∂∂ = = = −); in these

systems, called Chaplygin systems, the equations of motion can be separated from the

non-integrable constraint equations. We preserve the denomination of Chaplygin

systems also for the non-conservative systems with general non-holonomic constraints

(non-catastatic, for which

≠

a ), if the generalized forces and the coefficients

do not depend explicitly on the co-ordinates

++12

, ,...,

qq q . The motion of the skate,

the motion of a circular disc on a plane and the motion of the two-wheeled carriage,

considered in the previous section, correspond just to such systems.

Obviously, the constraint relations (22.2.88) allow to write the relations

δ= δ= −

∑

, 1,2,...,

hk hkj

qcqk sh

(22.2.88')

for the virtual generalized displacements, the virtual generalized displacements

δδ δ

, ,...,

qq q being independent too.

Starting from the d’Alembert-Lagrange theorem (18.2.27'), written in the form

hsh

kh hk

hk hk

TT T T

Qq Q q

tq q tq q

−

∂∂ ∂ ∂

⎡⎛ ⎞ ⎤

−−δ+ − − δ=

⎜⎟

⎢⎥

∂∂ ∂ ∂

⎣⎝ ⎠ ⎦

∑∑



using the relations (22.2.88') and observing that in a double sum one can invert the

order of summation, we obtain

−

∂∂ ∂

⎡⎛ ⎞ ⎤

⎛⎞

−−+ δ=

⎜⎟

⎢⎥

∂∂ ∂

⎝⎠

⎣⎝ ⎠ ⎦

∑∑

hsh

hkj

TT T

Qc q

tq q tq



;

MECHANICAL SYSTEMS, CLASSICAL MODELS

468

but the virtual generalized displacements which intervene are independent so that one

can write

−

∂∂ ∂

⎛⎞

−+ = =

⎜⎟

∂∂ ∂

⎝⎠

∑

, 1,2,...,

hkj

TT T

cQjh

tq q tq

(22.2.89)

We denote by an asterisk an expression in which the generalized velocities

++12

, ,...,

qq q 

, hence the generalized velocities which are considered as dependent,

have been eliminated by means of the constraint relations (22.2.88). We can thus write

−

∂∂ ∂

∂

∂∂ ∂

∂∂ ∂ ∂

∑

∑∑

hkj

sh h

hkl

jj j

TT T

qq q

TT T

qq q q

 



where we took into account

∂

∂∂

∂∂∂

∑

hkj

hk hk

hkj l

qqq





;

observing that

∂

∑

hkj

hkj l



we can also write

111

dd d

sh sh h

hkl

hkj l

hk hk l

kkl

TT TT

tq tq tq q q

−−

===

∂

⎛⎞

∂∂ ∂∂

⎛⎞

=+ +

⎜⎟

∂∂ ∂∂∂

⎝⎠

∑∑∑



 

The equations (22.2.89) can be rewritten in the form

, 1,2,..., ,

sh h

hkl hkj

jj j

hk l

TT T

qQj h

tq q q q q

−

∂∂

⎛⎞∂∂ ∂

⎛⎞

−+ − = =

⎜⎟

∂∂ ∂ ∂ ∂

⎝⎠

∑∑





(22.2.89')

obtaining thus Chaplygin’s equations presented in 1895 at a conference and published

in 1897. Eliminating the generalized velocities

++12

, ,...,

qq q  from the expressions

∂∂/

Tq by means of the constraint relations (22.2.88), the system (22.2.89')

becomes of

h differential equations and with h unknown functions

( ), ( ),..., ( )

qtqt qt, a number equal to the number of degrees of freedom of the

mechanical system. These unknown functions are thus determined independently of the

Dynamics of Non-holonomic Mechanical Systems

469

dependent generalized co-ordinates

++12

( ), ( ),..., ( )

qtqt qt, which can be

subsequently obtained, by

s quadratures, from the constraint relations (22.2.88).

If the constraint relations are integrable (holonomic), hence if

∂∂

===−

∂∂

, , 1,2,..., , 1,2,...,

hkl hkj

jl h k s h

(22.2.90)

then Chaplygin’s equations are reduced to Lagrange’s classical equations.

Putting in evidence the conservative part

∂∂/

Uqand the non-conservative part

of the generalized forces (see formula (18.2.24)), one can introduce the kinetic potential

=+TUL , so that Chaplygin’s equations read

, 1,2,..., .

sh h

hkl hkj

jj j

hk l

qQj h

tq q q q q

−

∂∂

⎛⎞∂∂ ∂

⎛⎞

−+ − = =

⎜⎟

∂∂ ∂ ∂ ∂

⎝⎠

∑∑





LL L

(22.2.89'')

Let us write now the equations of motion of the skate (see Sect. 22.2.3.1). We

choose as independent generalized co-ordinates the co-ordinates

qx and

q θ

the dependent co-ordinate

qx being specified by the constraint relation

tanxx θ .

Observing that

21 23

tan , 0ccθ==, we can write the equations (22.2.89'') ]n the

form (only the derivative

∂∂=

/1/cosc θθ is non-zero)

()

⎛⎞

∂∂∂

⎛⎞

−+ − =

⎜⎟

∂∂∂

⎝⎠

⎛⎞

∂∂∂

⎛⎞

−+ =

⎜⎟

∂∂

∂

⎝⎠

112

cos

tx x x







LLL

In this case, the kinetic potential is given by (we use the formula (22.2.37))

()

2cos 2

MIθ



and one obtains

tan 0, 0xxθθ θ+==



  ,

being led to the same results as in Sect. 22.2.3.1.

We can consider also a somewhat more general case in which the skate, of weight

, slides on the plane

Ox x

, inclined with the angle α with respect to the

horizontal line (Fig. 22.16). Chaplygin’s equations are the same, Lagrange’s function

being given by

MECHANICAL SYSTEMS, CLASSICAL MODELS

470

=++

sin

cos

MImgx

θα



;

besides the equation

= 0θ



, we find

tan sin cosxx gθθ α θ



 

Assuming that

0 , we get

()

=−

22 2

( ) sin , sin ,

() 2 sin2 ;

xt a ta

xt a t t

ωα

ωω

(22.2.91)

hence, the skate

AB has a uniform motion of rotation about the contact point C ,

which – in its displacement – describes a cycloid.

Fig. 22.16 Motion of a skate on an inclined plane

We can associate to the independent generalized co-ordinates

, ,...,

qq q other

independent parameters, that is quasi-co-ordinates

, ,...,

ππ π, by means of the

relations (the Greek indices are summed from

1toh , according to the summation

convention of the dummy indices)

= q

γγεε

πα,

(22.2.92)

of the form (22.2.17), where

( , ,..., ), , 1,2,...,

qq q h

γε γε

αα γε==.

Using these relations and the

−shconstraint relations (22.2.88), we can express all

the generalized velocities by means of the

h quasi-velocities in the form

==, 1,2...,

qjs

βπ .

(22.2.92')

To the virtual generalized displacements correspond relations of the form

δ= =, 1,2...,

qjs

βπ ,

(22.2.92'')

Dynamics of Non-holonomic Mechanical Systems

471

where

π are the virtual variations of the quasi-co-ordinates. Taking into account

these relations, the d’Alembert–Lagrange theorem

∂∂

⎡⎛ ⎞ ⎤

−δ=

⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎦

tq q



leads to

∂∂

⎡⎛ ⎞ ⎤

−==

⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎦

0, 1,2,...,

tq q

βσ



where the Latin indices are summation indices from

1 to s , corresponding to

Einstein’s convention of summation, while

12 12

( , ,..., , , ,..., )

qq qqq q LL is

Lagrange’s kinetic potential.

Taking into account (22.2.92''), we get

∂

∂∂∂ ∂∂

=+ =

∂∂∂∂ ∂∂

qqqq q

γγ γ σ

πβ





LLL LL

wherefrom

∂

∂∂ ∂

=−

∂∂∂∂

∂

⎛⎞∂∂∂

⎛⎞

=−

⎜⎟

∂∂∂∂

⎝⎠

qqqq

tq t qq

γε γε σ

γγ

γσ σ

εγ

ββ βπ

ββπ





LL L

LLL

with

==1,2,..., , , , 1,2,...,js hγεσ . We notice ∂∂ =∂∂(/) (/)

jj j

γε σ σ σ

εε

ββπβππ,

to which we associate two other analogous relations; we can thus write

∂∂∂∂

∂∂

jjjj

εεσσ

γσ γε

γσγε

γσ

ββββ

ββ

ππ

Replacing in the equations of motion, it results

∂

⎛⎞∂∂∂

⎛⎞

−+ − =

⎜⎟

⎜⎟⎜ ⎟

∂∂∂∂∂

⎝⎠

γγ γσ

ππ ππ





LLL

(22.2.93)

with

1,2,..., , , 1,2,...,

shγσ==

; we obtain thus Chaplygin’s equations in

quasi-co-ordinates. If the quasi-co-ordinates are true co-ordinates

, , 1,2,...,h

γε γε

βγε=δ =

(we introduce Kronecker’s symbol), so that the equations