Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

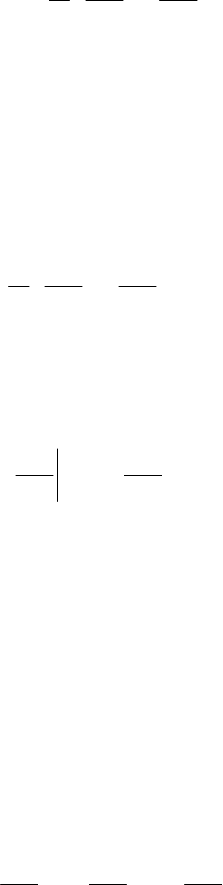
MECHANICAL SYSTEMS, CLASSICAL MODELS

492

introducing the virtual generalized displacements, the relations (22.4.2) take the form

(22.2.88').

Supposing that at least a percussive generalized force intervenes, the generalized

velocities

′

q at the initial moment

′

become

′′

q at the final moment

′′

The d’Alembert–Lagrange theorem becomes

⎡⎛ ⎞ ⎤∂∂

−−−δ=

⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎦

∑

QR q

tq q

(22.4.3)

where

is the kinetic energy, which is written taking into account the constraint

relations (22.4.2) (eventually, the quasi-velocities);

Q and , 1,2,...,

Rj h= , are the

given and the constraint (which appear only in the non-holonomic case) generalized

forces, respectively. By introducing the constraint generalized forces, the constraint

relations (22.2.88') have been eliminated, so that, in (22.4.3), the virtual generalized

displacements are independent; we are thus led to the system of

h differential

equations

⎛⎞

∂∂

−=+ =

⎜⎟

∂∂

⎝⎠

, 1,2,...,

QRj h

tq q

(22.4.3')

which describe the motion of the non-holonomic system (the motion of the

representative point

P in the space

Λ ), at any moment t (including the moments

′′′

∈ [, ]ttt

). Integrating on the collision interval, we can write

()

′′

′′ ′′

′′

′

∂∂

−=+=

∂∂

∫∫

d d , 1,2,...,

tQRtj h

qq

A mean value theorem applied to an integral the integrand of which is a finite quantity

allows to neglect the integrals which result from the non-percussive part of the given

generalized forces and from the constraint generalized forces (which are, as well, finite,

as it has been shown by Beghin and Rousseau in 1903 for a non-holonomic mechanical

system with ideal constraints), as well as from the partial derivatives

/ , 1,2,...,

Tqj h∂∂ = .

Defining the generalized percussion in the form (see Sect. 18.3.1.8 too)

′′

′

′′ ′

−→+

∫

lim d , 1,2,..,

Qtj hP ,

(22.4.4)

we get, finally,

′′ ′

⎛⎞⎛⎞⎛⎞

∂∂ ∂

Δ= − ==

⎜⎟⎜⎟⎜⎟

∂∂ ∂

⎝⎠⎝⎠⎝⎠

** *

,1,2,...,

jj j

TT T

qq q 

P .

(22.4.5)

Dynamics of Non-holonomic Mechanical Systems

493

Hence, in the collision phenomenon, the equations (22.4.5) of the non-holonomic

mechanical systems have the same form as those used for the holonomic

ones (see

Sect. 18.3.1.8); as a difference, in case of the non-holonomic mechanical systems, the

system is reduced with

−sh

constraint relations, while

contains only independent

parameters, the functions being expressed by means of the relations (22.4.2).

Writing the constraint relations (22.4.2) for the ends of the collision interval, we

obtain, by subtraction (the kinematic coefficients are constants),

Δ= Δ= −

∑

,1,2,...,

hk hkj

qcqk sh ,

(22.4.6)

′′ ′

Δ= − =,1,2,...,

qqqj h .

(22.4.6')

The generalized velocities at the start of the collision phenomenon

, 1,2,...,

qi s

′

= ,

and the generalized percussions

, 1,2,...,

h=P

, are known; the unknown

generalized velocities

, 1,2,...,

qj h

′′

 , at the end of the collision phenomenon, will

be given by the relations (22.4.5), while the other generalized velocities

, 1,2,...,

qk sh

′′

=−

, will be given by the relations (22.4.6), (22.4.6').

The collision phenomenon considered above corresponds to the intervention of some

percussive forces. We consider now the case of a sudden application of some

non-holonomic constraints.

Let thus be a mechanical system subjected to no one percussive force, which after

eliminating the holonomic constraints, has

s degrees of freedom and is represented in

the space

Λ by the representative point P , specified by the generalized co-ordinates

, ,...,

qq q. If, at the moment

′

, we introduce −sh ideal non-holonomic relations of

the form (22.4.2), then the virtual generalized displacements will be linked by the

relations (22.2.88'), so that

h of them can be considered to be independent. Taking into

account these relations, the d’Alembert–Lagrange theorem (22.4.3) reads

{

−

+++

⎛⎞

∂∂∂

+−−−

⎜⎟

∂∂∂

⎝⎠

⎡⎛⎞⎤⎫

∂∂

−+++δ=

⎬

⎜⎟

⎢⎥

∂∂

⎣⎝⎠⎦⎭

∑∑

∑

***

hsh

hkj

hkj hk hk

hk hk

TTT

cQR

tq q q

cQRq

tq q



(22.4.7)

integrating with respect to time on the collision interval

′′′

[, ]tt

and making the same

considerations as above (given generalized forces and finite constraints, finite partial

derivatives

/ , 1,2,...,

Tqi s∂∂ = , constant kinematic coefficients, independent

generalized displacements), we obtain the system of algebraic equations

−

⎛⎞ ⎛ ⎞∂∂

Δ+Δ ==

⎜⎟ ⎜ ⎟

∂∂

⎝⎠ ⎝ ⎠

∑

0, 1,2,...,

cjh

qq

(22.4.8)

MECHANICAL SYSTEMS, CLASSICAL MODELS

494

′′ ′

⎛⎞⎛⎞⎛⎞

∂∂ ∂

Δ= − =

⎜⎟⎜⎟⎜⎟

∂∂ ∂

⎝⎠⎝⎠⎝⎠

** *

,1,2,...,

jj j

TT T

qq q 

(22.4.8')

for the determination of the

s generalized velocities after collision.

Let us denote by



the function

considered as depending explicitly on the

generalized velocities

, ,...,

qq q 

and implicitly on them by the generalized velocities

++12

, ,...,

qq q 

, by means of the constraint relations (22.4.2); in this case, the

equations (22.4.8), (22.4.8') can be written, formally, in a compact form

′′ ′

⎛⎞⎛⎞⎛⎞

∂∂ ∂

Δ= − ==

⎜⎟⎜⎟⎜⎟

∂∂ ∂

⎝⎠⎝⎠⎝⎠

** *

0, 1,2,...,

jj j

TT T

qq q

 

 

(22.4.9)

One must give a special attention to these equations, because one cannot eliminate

the generalized velocities

++12

, ,...,

qq q , effecting then the differentiation with

respect to the other generalized velocities; indeed, the constraints (22.4.2) take not place

for

′

<tt

, so that these ones cannot be used to eliminate the generalized velocities

mentioned above from the expression

′

∂∂ =

( / ) , 1,2,...,

Tqj h



 . In what concerns

the elimination of these generalized velocities from the expressions

′′

∂∂

(/)



1,2,...,

, corresponding to the end of the collision phenomenon, there can arise

two situations: the non-holonomic constraints suddenly applied (i) continue to act or

(ii) disappear for

′′

>tt

. The case (i) corresponds to a plastic collision, for which

= 0k , while the case (ii) corresponds to a perfect elastic collision, for which = 1k ; k

is the restitution coefficient (see Sect. 10.1.1.1). In general, we can have

<<01k .

Obviously, the generalized velocities at the beginning of the collision phenomenon

, ,...,

qq q  are known; to determine the generalized velocities which result at the end of

the phenomenon of collision we proceed in a different way, as

= 0k or <<01k . So, in

the first case, the constraints (22.4.2) are maintained for

′′

>tt

too and we can eliminate

the generalized velocities from

(/), 1,2,...,

Tq j h

′′

∂∂ =



 , the problem being thus

completely solved. In the second case, one cannot make the elimination mentioned above,

having to our disposal

h algebraic equations

′′ ′′ ′′

,,...,

qq q ; the other generalized

velocities

′′ ′′ ′′

, ,...,

qq q  will be specified by the relations (22.4.2), the problem

being thus completely solved. In the second case, one cannot make the elimination

mentioned above, having to our disposal h equations (22.4.9) for s unknowns

′′ ′′ ′′

, ,...,

qq q ; it is necessary to associate other −sh relations of physical nature,

obtained – eventually – on an experimental way, to can solve the problem.

The problem becomes more complicated if, beside the non-holonomic constraints –

which can be also non-ideal – appear percussive forces too. In the case

= 0k we have

s unknown percussions and −− =()ssh h generalized velocities at the end of the

collision phenomenon, as well unknown; hence, there are

+sh unknowns to be

determined. For this, we have at our disposal

h equations of dynamical equilibrium

Dynamics of Non-holonomic Mechanical Systems

495

(22.4.5) and

−sh constraint relations (22.4.2); we need other h relations, which can be

obtained assuming that the constraints are ideal (

−− =()ssh h relations) or imposing

other supplementary conditions of physical nature. In the case

<≤01k we have also

+− =()hsh s equations at our disposal; but the number of the unknowns is 2s

(

s percussions and s generalized velocities at the end of the collision). The condition of

ideal constraints involves only

h relations, so that there are still necessary −sh relations

of physical nature to solve the problem.

The above results are valid for discrete mechanical systems (systems of particles or

systems of rigid solids).

22.4.1.2 Applications

We consider, in what follows, some simple applications, which present a certain interest

in themselves.

Let be thus a rigid solid which slides on a horizontal plane and is acted upon by a

percussive force contained in the plane and normal to the direction of advance. We idealize

the rigid solid by a skate of mass

M which slides on the plane

, Ox x A being the

contact point,

the mass centre ( =AC a ), the percussion force

acting at the point

B (

=AB b

) (Fig. 22.18); the position of the skate will be specified by the point

(, )Ax x and by the angle θ made with the

Ox -axis. As we have seen in Sects. 3.2.2.6

and in 22.2.3.1, the constraint relation is of the form

tanxx θ .

(22.4.10)

Fig. 22.18 Motion of a skate on a horizontal plane, acted upon by a percussive force

The co-ordinates of the mass centre are given by

cos

xxaθ ,

sin

xxaθ ; in this case, corresponding to the formula (22.2.37), we can

express the kinetic energy in the form

()( )

⎡⎤

=−++ +

⎣⎦

sin cos

TMxa xa i

θθ θθ θ





(22.4.11)

where

i is the gyration radius with respect to the mass centre. Taking into account the

constraint relation (22.4.10), it results

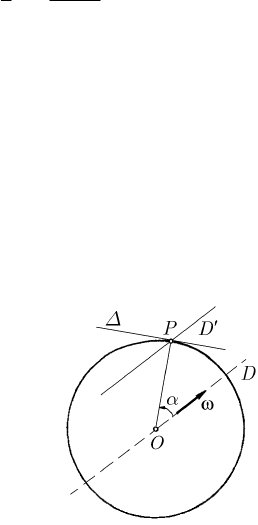
MECHANICAL SYSTEMS, CLASSICAL MODELS

496

()

⎡

⎤

=++

⎢

⎥

⎣

⎦

*222

cos

TM ai



(22.4.11')

The work effected by the percussion

is given by

δ=− δ+ δ+δ=δ

sin cosWP xP xPb Pbθθθθ,

so that the generalized percussions will be

0, Pb

== =PP P . Assuming that the

skate is at rest at the beginning of the collision phenomenon, the equations (22.2.5) with

(22.4.11') lead to

()

0, xx Mai Pbθ

′′ ′′ ′′

== + =





(22.4.12)

Fig. 22.19 Motion of a homogeneous circular disc, which

is rotating about one of its diameters

Let us consider now a homogeneous circular disc of mass

M and radius a , which is

rotating with an angular velocity

ω about a diameter

of it. At a certain moment, the

point

P of the circumference, specified by the angle α and the distance sina α with

respect to the axis

(Fig. 22.19), is suddenly stopped; the velocity of this point at the

respective moment is

sinaωα, while the moment of momentum with respect to the

axis

′

which passes through P and is parallel to D is given by

′

(1/ 4)

KMaω (the moment of inertia with respect to the axis D is

(1/ 4)

IMa), remaining unchanged after stopping the point

. In this case, the

moment of momentum with respect to the axis

Δ , tangent at P to the circumference is

(1/ 4) sinKMa

ωα. Starting from the moment of inertia

and applying the

Huygens–Steiner theorem (see Sect. 3.1.2.6), we obtain the axial moment of inertia

(5/4)IMa

and then the angular velocity =/(1/5)sinKI

ΔΔ

ωα, hence a

velocity which is the fifth part of the initial velocity of the point

P .

Let be, as well, a homogeneous sphere of radius

a , which moves freely in the space

and which, at the initial moment

′

strikes a rough horizontal plane

′′′

Oxx (the

′′

Ox -axis is directed towards the part from which comes the sphere, the considered

frame of reference being fixed). After collision, the sphere remains on the plane and can

Dynamics of Non-holonomic Mechanical Systems

497

have a motion of pivoting or of rolling without sliding; there are thus imposed the

constraint relations (see Sect. 22.2.3.3, formula (22.2.57'))

12 21 3

0, 0, 0xa xa xωω

′′ ′′ ′

−= −= =

(22.4.13)

according to which the velocity of the contact point vanishes. Introducing Euler’s

angles

,,ψθϕ

and using the relations (5.2.35') which are linking the components of the

rotation velocity vector

along the axes of the fixed frame of reference to these

angles, we can write three constraint relations in the form (see the formulae (22.2.57'')

too)

()

′

=−

′

=− −

′

sin sin cos ,

cos sin sin ,

θψϕθψ











(22.4.13')

the first two relations being non-holonomic. The kinetic energy is given by

()

′′′ ′′′

=+++++

⎡⎤

⎣⎦

22222 2 2

123 123

TMxxxi

ωωω ,

(22.4.14)

where

i is the gyration radius with respect to a diameter; taking into account the

relations (5.2.35'), it results

()

=++++++

⎡⎤

⎣⎦

2222222

123

2cos

TMxxxiψθϕ ψϕθ

 

  

(22.4.14')

By means of the relations (22.4.13'), we can write

()

cos ,

sin cos ,

cos sin c

TTT T

Mi ax x

TTT T

Mi a x

ψϕ θ

ψψ ψ ψ

θψψ

θθ θ θ

ϕϕ ϕ ϕ

ϕψ θ θ

′′

∂∂

∂∂∂ ∂

=+ + = +

′′

∂∂

∂∂ ∂ ∂

′′

∂∂

∂∂∂ ∂

′′

=+ + = + −

⎡

⎤

⎣

⎦

′′

∂∂

∂∂ ∂ ∂

′′

∂∂

∂∂∂ ∂

=+ +

′′

∂∂∂∂∂∂

′

=+−





  







  









()

os sin ;xψψ

′

⎡⎤

⎣⎦



in this case, the equations (22.4.8') read

()

() ()

()

() ()

′′ ′′ ′ ′

+=+

⎡ ′′⎤

′′ ′ ′ ′

+=+ −

⎣⎦

′′ ′′

⎡ ′′⎤

′′ ′ ′

=+ − −

⎣⎦

22 2

222 2

cos cos ,

sin cos ,

sin cos

cos cos sin sin ,

ia i ax x

ia i

iaxx

ψϕ θψϕ θ

θθ ψ ψ

θϕ ψ θ

ϕψ θ ψ ψ θ







MECHANICAL SYSTEMS, CLASSICAL MODELS

498

where we took into account the constraint relations (22.4.13') which take place at the

end of the collision phenomenon and remain still valid. Hence, one obtains

()

{

()}

()

′′ ′ ′

=++

⎡⎤

⎣⎦

′′

′′ ′ ′ ′

=+−

⎡⎤

⎣⎦

′′ ′ ′ ′

=−+

⎡

⎤

⎣

⎦

22 22

cos sin

sin

cos sin cos ,

sin cos ,

sin cos sin ;

sin

ia a

ax x

iax x

iaxx

ψψϕθθ

ψψθ

θθψψ

ϕϕθψψ









(22.4.15)

taking into account (22.4.13') and (5.2.35'), we obtain the velocities of the centre of the

sphere, after collision, in the form

()

′′ ′ ′

′′

xiax

xixa





(22.4.16)

22.4.2 First Integrals of the Equations of Motion

We consider, in what follows, the forms taken by the first integrals of the systems of

equations of motion in case of non-holonomic constraints, as well as the possibility to

obtain them; some applications put in evidence the results thus obtained.

22.4.2.1 Determination of First Integrals

Starting from Lagrange’s equations for a holonomic mechanical system, we find, in

certain conditions, the first integral of Painlevé (18.2.61), the first integral of Jacobi

(18.2.63) or a first integral of Jacobi type (18.2.66), the last two ones being particular

cases of Painlevé’s first integral (see Sect. 18.2.3.4); the mechanical systems which

admit one of the two integrals are generalized conservative systems, for which the

generalized mechanical energy (18.2.68) is introduced. Jacobi’s first integral allows the

reduction of Lagrange’s system of equations (18.2.38) for a natural mechanical system,

to a system of equations corresponding to a mechanical system with a number of

degrees of freedom less with a unity (see Sect. 18.2.3.5). The existence of hidden

co-ordinates (the kinetic energy

T does not depend explicitly on these co-ordinates) or

of ignorable co-ordinates (Lagrange’s function

L does not depend explicitly on these

co-ordinates) allows, as well, the determination of first integrals; in this case,

corresponding to the Routh–Helmholtz theorem, the problem is reduced to the

integration of a system of equation of Lagrange for a mechanical system with a smaller

number of degrees of freedom (see Sects. 18.2.3.6 and 18.2.3.7).

In the case of a non-holonomic mechanical system for which one of the generalized

co-ordinates, let be

q , is ignorable ( ∂∂=/0

qL ) one can write a first integral

starting from Lagrange’s equations only if some conditions are fulfilled. We introduce

thus Chaplygin’s equations (22.2.89''), in which we assume that the non-conservative

Dynamics of Non-holonomic Mechanical Systems

499

forces

, 1,2,...,

Qj h= , vanish, the constraint relations being of the form (22.2.88).

These equations take the form of Lagrange’s equations for

if the relations

∂∂

==−=

∂∂

,,1

, 1,2,..., , 1,2,...,

hkl hk

kshlh

(22.4.17)

are verified. Introducing the function

( , ,..., )

hk hk

uuqqq by the relations

==−

∫

d , 1,2,...,

hk hk

ucqksh

(22.4.18)

where

q is an arbitrary constant, and using the relations (22.4.17), we can write

∂∂

∂

∂∂ ∂

∫∫

10 10

,1 ,

hk hkl

qq q

which leads to

()

∂

10 2

, ,...,

hkl hkl

ccqqq

;

replacing in (22.2.88), we obtain, finally,

()

++ +

∑ 10 2

d d , ,..., d

hk hk hkj

qu cqqqq.

(22.4.19)

Hence, in case of a non-holonomic mechanical system, we can write an equation of

motion corresponding to a certain generalized co-ordinate, in the form of an equation of

Lagrange type, if, in the non-holonomic constraint relations, it is possible to separate a

total differential, so that in the other constraint relations does no more appear the

respective generalized co-ordinate.

Let us consider now the system of equations of motion in quasi-co-ordinates (22.2.35),

with the notations (22.2.35'), written in the hypothesis in which the constraint relation are

catastatic, of the form (22.2.31); assuming that the generalized forces

, 1,2,...,

Qj s= ,

are conservative, we can introduce the kinetic potential

TUL , and the equations of

motion take the form

−

⎛⎞

∂∂ ∂

−+ == −

⎜⎟

∂∂ ∂

⎝⎠

∑

** *

0, 1,2,...,

kj k

jj j

jsm

γπ

ππ π





LL L

(22.4.20)

where

is a function of the generalized co-ordinates

, ,...,

qq q and, in general, of the

generalized quasi-velocities

, ,...,

ππ π 

. If the condition

−

∂

⎛⎞

−=

⎜⎟

∂∂∂

⎝⎠

∑

il im

mk l k

ββ π



(22.4.21)

MECHANICAL SYSTEMS, CLASSICAL MODELS

500

is fulfilled, then the equation (22.4.20), corresponding to the quasi-co-ordinate

π takes the

form of an equation of Lagrange; this condition is fulfilled if, e.g.,

0, 1,2,..., , 1,2,...,

isksmγ == = −. If, moreover, the quasi-co-ordinate

π is

ignorable (which takes place, e.g., if the kinetic energy

T does not depend explicitly on

any generalized co-ordinate), then one obtain a finite integral of the form

∂

const

π

(22.4.22)

Let us return to the equations (22.2.35), (22.2.35'), where

T is a function of the

generalized co-ordinates

, ,...,

qq q and, in general, on the generalized velocities

, ,...,

ππ π ; we notice that, due to non-holonomic constraints, we can equate to zero

the generalized quasi-velocities

0, 1,2,...,

smk

kmπ

−+

== , in the expressions

/ , 1,2,...,

Ti sπ∂∂ = , but only after effecting the differentiation. Multiplying each

member of the equation (22.2.35) by

π and summing, it results

−−

⎡⎛⎞ ⎤

∂∂

−=

⎜⎟

⎢⎥

∂∂

⎣⎝⎠ ⎦

∑∑

sm sm

jjj

ππ π

ππ

 



where we took into account that

−−

∑∑

0, 1,2,...,

smsm

kj k

isγππ ,

according to the relations (22.2.35) and to the fact that one can equate to zero the

generalized quasi-velocities

0, 1,2,...,

smk

kmπ

−+

== .

We notice that

−

⎛⎞

∂∂

⎜⎟

∂∂

⎝⎠

∑

***

TTT

ππ

 



because

T does not depend explicitly on time, having catastatic constraints. In general,

=++

****

TTTT,

(22.4.23)

where

is a quadratic form in the generalized quasi-velocities , 1,2,...,

jsmπ =− ,

is a linear form in the same generalized quasi-velocities, while

does not depend

on these generalized quasi-velocities; as well, Euler’s theorem for homogeneous

functions leads to

−

∂

∑

TTπ



Dynamics of Non-holonomic Mechanical Systems

501

Finally, we can write

()

−

⎡⎤

+− ++ =

⎣⎦

∑

** *** *

21 21

TT TTT Q

π ,

so that

()

−

−=

∑

** *

TT Qπ .

(22.4.24)

Assuming that the generalized forces

, 1,2,...,

Qj sm=−, derive from a simple

potential

U or from a generalized potential with the scalar part

U , we introduce the

potential energy

=−VU or =−

VU, respectively, so that

∂

=− = −

∂

, 1,2,...,

Qjsm

(22.4.25)

In this case, the relation (22.4.24) becomes

()

−+=

d0TTV

(22.4.24')

and we obtain the first integral of the generalized mechanical energy

=−+=

* TTVhE ,

(22.4.26)

where

E is the generalized mechanical energy, analogue to the first integral (18.2.68)

obtained in case of holonomic mechanical systems. If

0T , the kinetic energy

being, e.g., a quadratic form in the generalized quasi-velocities

−

, ,...,

ππ π 

, then the

first integral (22.4.26) is reduced to the first integral of the mechanical energy

=+=

*ETVh

(22.4.27)

22.4.2.2 Applications

Let be a circular disc, of radius R and mass M , which rolls without sliding on the fixed

horizontal plane

′′′

Oxx ; the

′′

Ox -axis is directed towards the part in which is the disc. A

movable system of axes has the pole at the centre

O of the disc, the

Ox -axis being normal

to its plane and the

Ox -axis being horizontal; the tangent to the disc at the contact point I

makes the angle

ψ with the

′′

Ox -axis, the axes

′′

Ox and

Ox make the angle θ , while

the angle

ϕ specifies the rotation of the disc (Fig. 22.20). The conditions at the contact

point are

dcosd, dsindxR xRψϕ ψϕ

′′

==.

(22.4.28)