Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

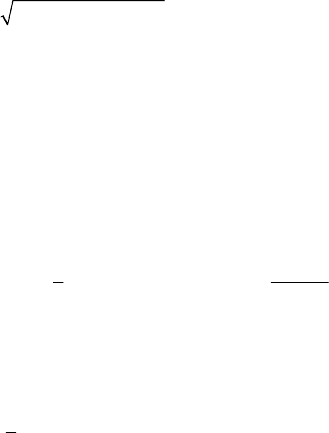
MECHANICAL SYSTEMS, CLASSICAL MODELS

512

d( , )PC ε<

(23.1.9')

for any

tt> , the point P corresponding to the solution being an arbitrary point of

the trajectory of the perturbed motion, then we say that the trajectory

C is orbitally

stable (or stable in Poincaré’s sense).

If the trajectory

is orbitally stable and if there exists

0δ >

, so that the condition

(23.1.9) holds and the condition

lim d( , ) 0

→∞

(23.1.9'')

be also involved, then we say that the trajectory

C is asymptotically orbitally stable;

hence, a perturbed curve tends to the curve

C in an infinite time.

23.1.1.2 Functions of a Definite Sign

We begin with some considerations concerning the functions of a definite sign,

which intervene in the study of stability problems.

Let be a uniform and continuous function

( , ,..., )

FFxx x= , defined in a

neighbourhood of the origin, so that

(0, 0,...,0) 0F = ; the co-ordinates

, 1,2,...,

xqi ns== =, can be the co-ordinates of a representative point P in the

configuration space

Λ . We say that the function F is positive definite (negative

definite) if, for

22 2

...

xx x h+++<, it takes only positive (negative) values and

vanishes only at the origin; if, without changing the sign, the function

( , ,..., )

FFxx x= vanishes also outside the origin, then we say that it is of constant

sign (positive or negative). For instance, the function

642

123

Fx x x=++ is positive

definite, while the function

()Fxx=− −

is of constant sign (negative).

One sees immediately that the origin represents a minimum (maximum) for a

positive (negative) definite function; hence, the derivative of first order vanishes at the

origin too, so that, in a Maclaurin expansion into series, we can write

...,

ij i j ij

Fcxxc

∂

=+=

∂∂

∑∑

(23.1.10)

where we have neglected the terms of higher order. The linear terms must vanish,

otherwise

F cannot be of a definite sign. The quadratic form

, , , 1,2,...,

ij i j ij ji

cxx c c ij n

∑∑

(23.1.11)

determines the sign of the function

F in a sufficiently small neighbourhood of the

origin, so that a study of it becomes necessary. Hence, if the quadratic form is positive

(negative) definite, then the function

F is positive (negative) definite too.

Stability and Vibrations

513

Sylvester’s criterion gives a necessary and sufficient condition for the quadratic form

to be positive definite. For this, let be the determinants

11 12

21 22

...

,1,2,...,

... ... ... ...

...

kk kk

cc c

Δ= =

(23.1.11')

introduced by Jacobi, starting from the matrix

[]

11 12 1

21 22 2

...

... ... ... ...

...

cc c

(23.1.11'')

If all the determinants are positive (

0, 1,2,...,

knΔ> = ), then the quadratic form

is positive definite (it can be written in the form of a sum of squares, after Jacobi’s

formula). If the function

F is negative definite, then the function F− is positive

definite and all the coefficients

c change of sign; in this case, the necessary and

sufficient condition that the quadratic form be negative definite is expressed by means

of the determinants

Δ too; the determinants of even index must be positive, while

these of odd index must be negative (

( 1) 0, 1,2,..,

kn−Δ> = ).

One can show that, if the function

F is of definite sign, then the surface

( , ,..., ) , const

FFxx x CC===, is a closed surface, the origin being in the

interior.

Observing that

( ), 1,2,...,

xxtk n==, it is useful to calculate also the total

derivative of the function

F with respect to time

iii

FFX

∑∑

(23.1.12)

where we have considered the equations

( , ,..., ), 1,2,...,

Xxx x i n

;

(23.1.12')

the sign of the function

d/dFt can give interesting informations concerning the

motion of the representative point

PnsΛ∈=.

Assuming that the function

F is positive definite, then the vector

gradF

is normal

to the surface

FC=

and is directed towards the exterior (in the increasing sense of

the function

F ); we can write

MECHANICAL SYSTEMS, CLASSICAL MODELS

514

grad

=⋅

(23.1.12'')

Fig. 23.3 The piercing of the surface FC= by the trajectory of the representative

point for

d/d 0Ft< (a) and for d/d 0Ft> (b).

too, where v is the velocity of the representative point

P . It results thus that: if

d/d 0Ft< , then the trajectory of the point P pierces the surface FC= from the

exterior towards the interior (Fig. 23.3a); if

d/d 0Ft> , then the trajectory of the

point

P pierces the surface FC= from the interior towards the exterior (Fig. 23.3b),

while if

d/d 0Ft= , d/d 0Ft> , then the trajectory of the point P is tangent to the

surface

FC=

(eventually, it can stay on this surface). If the function

is negative

definite, then one can make inverse affirmations.

23.1.1.3 Lagrange–Dirichlet Theorem

In Sect. 4.1.1.7 we have stated the Theorem 4.1.2, according to which the position of

equilibrium of a particle subjected only to the action of a given gravitational field is a

position of stable or instable (labile or indifferent) equilibrium, as this one has a

minimal or non-minimal (maximal or stationary) applicate, respectively. This result,

obtained by E. Torricelli in 1644, can be extended to the case of a mechanical system,

stating thus.

Theorem 23.1.1 (E. Torricelli). The position of equilibrium of a discrete mechanical

system

S , subjected only to the action of a given gravitational field, is a position of

stable, labile or indifferent equilibrium as the gravity centre of the system has a

minimal, maximal or stationary applicate (with respect to a frame of reference, one of

the axes of which is along the direction of action of the considered field – assuming that

it is uniform – having a sense opposite to this action).

This is the first important result concerning the stability of the position of

equilibrium of a mechanical system, which corresponds to a particular case of given

external forces (gravitational field, hence, own weight), but valid both for a discrete and

continuous mechanical system.

Let us try now to enlarge the frame of our study to the case of conservative forces,

starting from a simple potential. For this, we will deal only with a discrete mechanical

system

S , the configuration of which is specified by the representative point

, of

generalized co-ordinates

, ,...,

qq q, in the space of configurations

Λ . Let be

Stability and Vibrations

515

... 0

qq q====, the considered position of equilibrium. The potential function

(,,..., )

UUqq q= is determined neglecting an additive constant, which we choose

so as to have

(0, 0,...,0) 0UU==.

We suppose that the origin corresponds to an isolated point of extremum for the

function

U , let this one be a maximum; the respective point corresponds to a position

of equilibrium of the discrete mechanical system

S , because

0, 1,2,...,

Qjs

∂

===

∂

(23.1.13)

In this case, in a Δ -neighbourhood of the origin

| | , 1,2,...,

qj s<Δ =

, will take

place the strict inequality

( , ,..., ) (0,0,...,0) 0

UUqq q U=<=, assuming that not

all the generalized co-ordinates vanish simultaneously. The mechanical energy will be

expressed in the form

12 12

( , ,..., , , ,..., )

jk k

Eq q q q q q T U g qq U=−= −   ;

(23.1.14)

if at least a generalized velocity is non-zero (neither we assume that the origin is a

singular point, nor the

Δ -neighbourhood of the origin contains such a point), then we

have

0T > , so that it results 0E > in the Δ -neighbourhood of the origin, if not all

the canonical co-ordinates vanish. Hence, the mechanical energy has an isolated

minimum (equal to zero) at

O . Let be an arbitrary number ε so that 0 ε<<Δ and let

be the

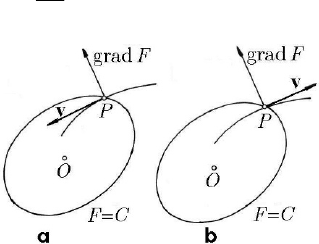
ε -neighbourhood defined by (Fig. 23.4, for 1s = )

, , 1,2,...,

qqj sεε<<= .

(23.1.15)

Fig. 23.4 Graphical representation of the Lagrange–Dirichlet theorem in the phase plane

The frontier of this neighbourhood being a closed set of points, the function

E attains

its minimum

∗

> 0E on this frontier, on which we will have, obviously,

MECHANICAL SYSTEMS, CLASSICAL MODELS

516

∗

−≥ >0EE ; but the continuous function E vanishes at the origin, hence it will

exist always a

δ -neighbourhood ( ≤δε) of the point O so that, in this

neighbourhood,

∗

<EE. Therefore, at the initial moment the conditions (23.1.1') hold,

then the initial mechanical energy

E verifies the relation

∗

EE; but the discrete

mechanical system is conservative, so that we have – at any moment –

EE, hence

∗

<EE too. Consequently, we can state that, in its motion, the representative point P

cannot reach the frontier of the

ε -neighbourhood on which

∗

≥EE, being always in

its interior, We can thus state (we introduce the potential energy

=−VU

)

Theorem 23.1.2 (Lagrange–Dirichlet). If, for a certain position of a conservative

mechanical system

S , the potential energy has an isolated minimum, then this

position is a position of stable equilibrium for it.

This theorem has been enounced by J.-L. Lagrange in 1788, is his famous treatise

“Mécanique analytique” and has been accurately proved, afterwards, by

P.G. Lejeune-Dirichlet. It has been shown in Sect. 4.1.1.7 for the case of a single

particle (Theorem 4.1.4) (Lagrange, J.L., 1788).

If the potential energy

has an isolated minimum, then the potential function

=−UV has an isolated maximum.

In case of non-conservative generalized forces, we use the general study made in

Sect. 18.2.1.3, adding to the conservative part of the force a non-conservative part, so

that

∂

=+ = =

∂

, ( , ,..., ), 1,2,...,

jjjj

QQQQqqqjs

(23.1.13')

If the power of the non-potential generalized forces

QqP

vanishes ( = 0P ),

then these forces are gyroscopic, being conservative (they derive from a generalized

potential, depending – obviously – on the distribution of the generalized velocities); one

can use the conservation theorem of mechanical energy (indeed,

ddWV=− ) , so that

the above proof does not change, the Theorem 23.1.2 remaining, further, valid. If

0<P , then the non-potential generalized forces are dissipative. The mechanical

energy

=−ETU decreases in time, in this case, so that ≤

EE (instead of

EE); if

∗

EE, then it results

∗

<EE too during the motion and further the

Theorem 23.1.2 can be enounced.

One must also show that, in the cases mentioned above (for which

≤ 0P ,

| | , 1,2,...,

qj s<Δ =

), the position of equilibrium is maintained. We assume, as

above, that the position of equilibrium takes place for

0, 1,2,...,

qj s== . We

assume also that, among the functions

, there exists at least one for which

≠(0,0,...,0) 0

Q ; in this case, due to the continuity, ≠ 0

Q in a Δ -neighbourhood

too. Because the canonical co-ordinates are independent, we can choose their values in

this neighbourhood so that

> 0P , which contradicts the hypotheses of gyroscopic

Stability and Vibrations

517

forces; we have thus a contradiction. Hence, by adding gyroscopic or dissipative forces,

the position of equilibrium remains the same.

We can apply the Theorem 23.1.2 to the example given before (the example in

Fig. 23.1 and the linear oscillator of equation (23.1.2)), the position of equilibrium

being a stable one.

One can show that the position of equilibrium of a conservative discrete mechanical

system (or to which gyroscopic or dissipative forces have been added) is, as well, stable

if the potential energy

corresponding to this position has a non-strict minimum, but

is such that, in any

ε -neighbourhood of the position of equilibrium, there exists a

closed hypersurface

( , ,..., ) 0

fq q q which contains this position and on which the

values of the potential energy

V are strictly greater than its value at the position of

equilibrium. For instance, a conservative system with one degree of freedom and a

potential energy

sin (1/ )Vq q

and =(0) 0V has the position

= 0q

as stable

position of equilibrium.

We have shown in Sect. 1.1.1 how can be expressed a condition of equilibrium by

means of a hypersphere

S of equation (23.1.5'); one can obtain thus a proof of the

Theorem 23.1.2 in a synthetic but rigorous form. We introduce an isoenergetic

hypersurface formed by the set of representative points

P (in the phase space

Γ ),

the canonical co-ordinates of which verify the condition

min

() ( ) , constEP EP c c−==;

(23.1.16)

the mechanical energy

()EP has an isolated minimum at

min

P and the constant c can

take arbitrary values (positive values on isoenergetic hypersurface which have points in

the neighbourhood of

min

P ). If = 0c , then the hypersurface is reduced to the point

min

P . The mechanical energy E is a continuous function so that, for increasing

positive, small values of

c , the corresponding isoenergetic hypersurfaces are closed,

each of them containing the point

min

P , as well as all the preceding hypersurfaces, in

the order in which the constant

c increases. Taking into account that the mechanical

energy is conserved during the motion (the generalized forces are conservative or

quasi-conservative), the representative point

P describes a curve situated on the

isoenergetic hypersurface which passes through

P , corresponding to the state of the

discrete mechanical system at the initial moment; the constant

c has the value

=−

min

() ( )cEP EP .

(23.1.16')

For the trajectory of the representative point

be in the interior of the hypersphere S

it is necessary and sufficient that to the initial perturbation of the state of equilibrium

does correspond a representative point

, which belong to an isoenergetic

hypersurface situated entirely in

; taking into account how the isoenergetic

hypersurfaces are situated around

min

, it results that such a choice of the initial

perturbation

P is always possible, the Theorem 23.1.2 being thus proved.

MECHANICAL SYSTEMS, CLASSICAL MODELS

518

In the case of a discrete mechanical system of

n particles, of masses

m , of weights

mg and applicates , 1,2,....,

zi n= , with respect to a horizontal plane (in opposite

sense to the gravity action), the potential energy is given by

−= = =

∑∑

ii i

UmgzMgzMm,

(23.1.17)

where

z is the applicate of the gravity centre, we find again Torricelli’s theorem ( −U

has an isolated minimum if the applicate

z is minimal). The theorem remains valid if,

besides particles, the discrete mechanical system contains rigid solids too.

23.1.1.4 Stability of the Equilibrium of an Autonomous Discrete Mechanical

System with One Degree of Freedom, in Linear Approximation

We begin the study of an autonomous discrete mechanical system with the most

simple case, that in which there is only one degree of freedom; the phase space

Γ has

two dimensions, the representative point

being of canonical co-ordinates

,qp

(the

generalized co-ordinate and the generalized momentum). Hamilton’s system of

differential equations can be written in the autonomous general form

112 212

(, ), (, )

Xxx Xxx

(23.1.18)

The Cauchy–Lipschitz theorem 19.1.2

of existence and uniqueness ensures us, in

sufficiently large conditions, that through any point of the phase space passes only one

integral curve of the system (23.1.18) (

11 22

(), ()xxtxxt==), which satisfies the

given initial conditions (in a Cauchy problem); hence, two integral curves cannot have

common points.

Let

1122

, xxαα== be a position of equilibrium so that

112

(, )X αα

212

(, ) 0X αα ; one can thus obtain all the positions of equilibrium. By the

translation

111222

, xx xxαα→+ →+ one obtains ==

(0,0) (0,0) 0XX ; one

can thus admit, without any loss of generality, that the origin represents a position of

equilibrium. Assuming that, in general,

≠

112

(, ) 0Xxx , we can write.

212

1112

(, )

d(,)

Xxx

xXxx

(23.1.18')

so that, at a regular point (for which

+≠

0xx ), the tangent to the integral curve is

well determined; if

0XX

, then the tangent is non-determined, having to do

with a singular point (e.g., the origin). We expand into a Maclaurin series and obtain

112 111 122 112

212 211 222 212

(, ) (, ),

Xxx ax ax Rxx

=++

(23.1.19)

Stability and Vibrations

519

where

,RR are remainders (higher powers of the variables

,xx) and where

=,, 1,2

aij , are constants.

In linear approximation, we consider the system (called the system of the first

approximation too)

=+ =+

11 1 12 2 21 1 22 2

ax ax ax ax

;

(23.1.20)

the corresponding characteristic equation is

11 12

21 22

det det 0

−

⎡⎤

⎢⎥

−

⎢⎥

⎣⎦

(23.1.20')

or, in a developed form,

−+ + − =

11 22 11 22 12 21

() 0aa aaaaλλ .

(23.1.20'')

The roots

λ and

λ of this equation are the eigenvalues of the matrix A and the form

of the integral curves in the neighbourhood of the position of equilibrium depends on

them.

The solution of the system of differential equations is, in this case, of the form

() ()

=+ = − +−

⎡

⎤

⎣

⎦

12 1 2

11 2 2 111 212

ee, e e

tt t t

x C C x aC aC

λλ λ λ

λλ,

(23.1.21)

where

,CC are two integration constants; by a change of axes, passing from the

orthogonal Cartesian system

Ox x to the oblique Cartesian system

Oξξ defined by

the relations

()()

[]

=+ = − + −

1122 111 212

,xx a a

ξξ λ ξ λ ξ,

(23.1.21')

one obtains the parametric representation

11 22

e, e

λλ

ξξ.

(23.1.21'')

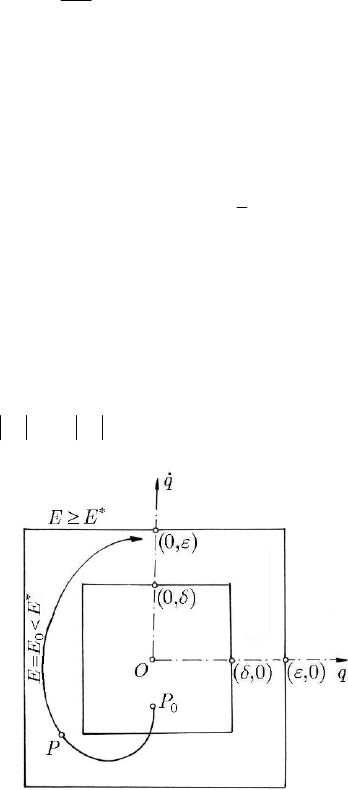
(i) Distinct real roots of the same sign. Eliminating the time

t between the equations

(23.1.21''), we get

Cξξ,

(23.1.22)

where

/n λλ, and C is a new integration constant, specified by the initial

conditions; the curve are parabolas of degree

n .

MECHANICAL SYSTEMS, CLASSICAL MODELS

520

||||λλ, then it results > 1n , and the parabolas tend to be tangent at the

origin to the

Oξ -axis (Fig. 23.5a); if >

||||λλ, then it results < 1n and the

parabolas tend to be tangent at the origin to the

Oξ

-axis (Fig. 23.5b). The respective

singular point is called node.

Fig. 23.5 Representation of the solution for real positive distinct eigenvalues λ:

(a)

λλ<

; (b)

λλ>

, around an instable node

If the roots

λ and

λ are both positive and if t increases, then the representative

point moves away from the singular point, which is an instable node (Fig. 23.5), while

if the roots

λ and

λ are both negative and if t increases, then the representative

point comes close to the singular point, which is – in this case – a stable asymptotic

node (Fig. 23.6).

Fig. 23.6 Representation of the solution for real negative distinct eigenvalues λ:

(a)

λλ< ; (b)

λλ> , around a stable node

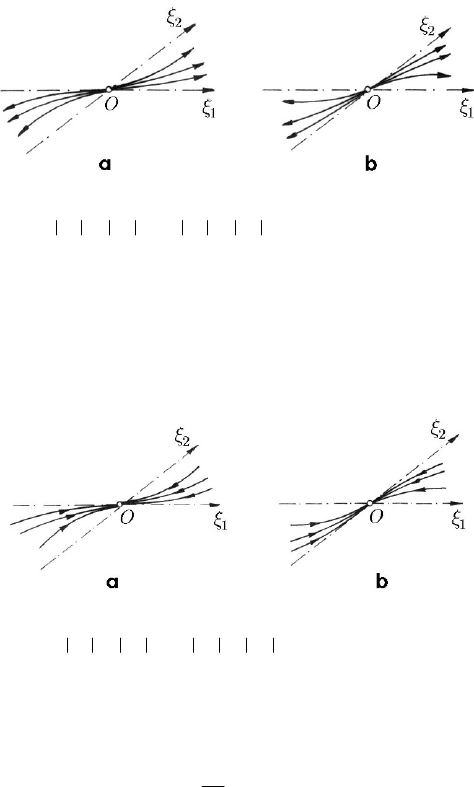
(ii) Real roots of opposite signs. Assuming that

0, 0λλ>< and denoting

=−

/n λλ, we obtain curves of the form

(23.1.22')

hence a family of hyperbolas of degree

n . The singular point is called saddle

(Fig. 23.7). If

→∞t , then →∞

ξ and →∞

ξ , the representative point moving off

from the origin. A saddle point is instable. If

0, 0λλ<>, then the trajectories are

the same, but they are traveled through in an inverse sense. We mention that, in the first

Stability and Vibrations

521

case, the

Oξ -axis is a stable variety (Fig. 23.7), while, in the second case, the

Oξ -axis is such a variety.

Fig. 23.7 Representation of the solution for real eigenvalues λ of opposite signs,

around an instable saddle point

(iii) A non-zero root and a zero root. Let

λλ and =

0λ be the roots; we can

write

1122

ξξ.

(23.1.23)

The trajectories in the phase plane are semi-straight lines parallel to the

Oξ -axis,

which start from the vicinity of the

Oξ -axis if > 0λ (Fig. 23.8a) or tend to this axis

for

→∞t if < 0λ (Fig. 23.8b). Outside the origin, there are still positions of

equilibrium on the

Oξ -axis, for =

0C and

C arbitrary.

Fig. 23.8 Representation of the solution for the eigenvalues

λλ=

0λ =

(a) 0

λ > ; (b) 0λ < .

(iv) Double roots. In case of a double root, obvious real, we have

λλλ. We

distinguish two subcases:

(a) The equations are uncoupled and we can use the results of case (i) with

= 1n .

The trajectories of the representative point form a family of semi-straight lines,

concurrent at the origin; if the roots are positive and

t increases, then the representative

point moves away from the origin, obtaining a unstable star (Fig. 23.9a), while if the