Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

452

we get, successively,

= ()tψψ and = ()tϕϕ . By means of the constraint relations

(22.1.3'), we can calculate the co-ordinates

′

x and

′

x too.

The problem can be formulated also in the quasi-co-ordinates

1234

,,,,πππππ

defined by the relations

=+ ==

=+ =+

11223

41 2

dcosdsind,dd,dd,

dd cosd,dd sind;

xR xR

πψ ψπψπθ

πψϕπψϕ

(22.2.56)

one can thus write the corresponding equations of Lagrange.

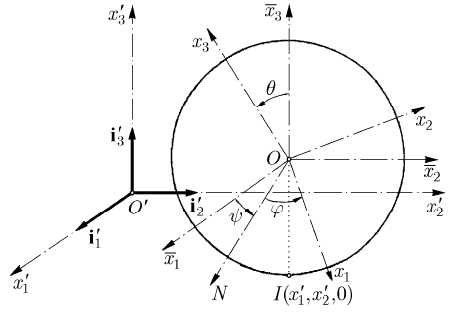
22.2.3.3 Motion of a Sphere on a Horizontal Plane

Let be a heavy rigid sphere of radius R and mass

, which can have a rolling and

pivoting motion on a fixed plane

′′′

Oxx , linked to the fixed frame of reference

′

R ,

the co-ordinates

′′

,xx corresponding to the contact point I with this plane; we take

the origin

O of the movable frame R at the centre of the sphere, the positions of its

axes with respect to the fixed frame being specified by Euler’s angles

,,ψθϕ. The

motion of the sphere can be thus studied in the space

Λ , the generalized co-ordinates

being

′′

,,,xxψθ and ϕ (Fig. 22.13).

Fig. 22.13 Motion of a sphere on a horizontal plane

Assuming that the sphere is rolling and pivoting without sliding on the fixed plane,

we can equate to zero the velocity of the contact point

′′

=+×=

OI 0

ω ;

(22.2.57)

observing that

12 3

, , , ,

OOj O O O

xxxxxxROIR

′′′′ ′′ ′′ ′

=====−

ri i

, we can

write the above condition in the form

()

′′′′′

−− =

rii

21 12

dd0

Rtωω .

(22.2.57')

Dynamics of Non-holonomic Mechanical Systems

453

We project on the axes of the movable frame and find the constraint relations (by means

of the formulae (5.2.35'))

()

′

=−

′

=− +

d sin d sin cos d ,

dcosdsinsind.

ψθ θ ψϕ

(22.2.57'')

Let us assume that the equations (22.2.57'') admit an integrable combination; in this

case, by integration, we get

()

′′

,,,, 0fxx ψθϕ .

Taking into account the conditions (22.2.57''), the differential consequence

∂∂∂∂∂

′′

++++=

′′

∂∂∂∂∂

d d ddd0

fffff

ψθ ϕ

ψθϕ

must be identically satisfied. Hence, besides the condition

∂∂=/0f ψ we will have

∂∂ ∂

⎛⎞

+−=

⎜⎟

′′

∂∂ ∂

⎝⎠

∂∂∂

⎛⎞

−+=

⎜⎟

′′

∂∂∂

⎝⎠

sin cos 0,

sin cos sin 0.

ff f

fff

ψψ

θψ ψ

Differentiating the above relations with respect to

and taking into account

∂∂=/0f ψ , we see that the brackets in these relations vanish, so that

∂∂=∂∂=//0ffθϕ; we obtain, from (22.2.57''), also

′′

∂∂=∂∂ =

//0fx fx . It

results that the function

f does depend on no one of the five generalized co-ordinates.

We can thus state that the considered rigid sphere represents a non-holonomic and

scleronomic mechanical system with three degrees of freedom. Such a problem is put,

e.g., in the study of motion of a billiard ball.

We can write the constraint relation (22.2.57'') in the form

()

′

−− =

′

++ =

sin sin cos 0,

cos sin sin 0,

θψϕθψ









(22.2.57''')

the generalized co-ordinates being

′′

=====

11223 4

,,,,qxqxq q qψθϕ; by

comparing the constraint relations (22.2.14) with (22.2.57'''), we get

== ==

=− =

====

10 11 12 13

14 15

20 21 22 23

24 25

0, 1, 0, 0,

sin , sin cos ,

0, 0, 1, 0,

cos , sin sin .

aa aa

aRaR

aaaa

aR aR

ψθψ

The kinetic energy is given by (

===

123

(2/5)III MR, formula (3.1.27))

MECHANICAL SYSTEMS, CLASSICAL MODELS

454

()()

()

′ ′′ ′′′

=++ ++

⎡⎤

′′

=+++++

⎢⎥

⎣⎦

22 2222

12 1 2 3

22 2222

2cos ,

TMxx MR

Mx x R

ωωω

ψθϕ ψϕθ



 

  

(22.2.58)

where we took into account the formula (5.2.35'). Assuming that the fixed plane is

horizontal, we notice that the work of the own weight vanishes (

==0, 1,2, 3,4,5

Qj );

Lagrange’s equations with multipliers (22.2.13) will be

()

′′

== +=

11 22

,, cos0

Mx Mx

λλψϕθ



  

(22.2.59)

()

+=−−

cos sin cos

MR θψϕ θ λ ψλ ψ

 



(22.2.59')

()

+= +

cos cos sin sin

ϕψ θ λ ψλ ψ θ



(22.2.59'')

The first two equations (22.2.59) specify the motion of the centre

O of the sphere in

the plane

′

constxR , the trajectory being rectilinear and the motion uniform; the

third equation (22.2.59) leads to a first integral of the moment of momentum in the

form (we take into account the formula (5.2.35'))

′

+=+ =

cos , const

AA K

ψϕ θ ,

(22.2.60)

where

′

K is the constant component of the moment of momentum along the

′′

Ox -axis.

Because

′

constx , it results a potential = constU , so that the conservation

theorem of mechanical energy is reduced to

′

=Th

, = consth , hence to

()

′′

++ +++ =

22 2222

2cos

xx R

ψθϕ ψϕθ

 

  

Taking into account the constraint relations (22.2.58), one can write the above first

integral in the form

()()

+=++ =

222 222

72 2

sin cos 2 cos

θϕ θ ψϕ θψϕθ



;

finally, by means of the first integral (22.2.60), the first integral of mechanical energy

becomes

()

′

+== −

222 22

sin , 2

BB hAK

θϕ θ



(22.2.61)

From the first two equations (22.2.59) and from the relation (22.2.57'''), it results

Dynamics of Non-holonomic Mechanical Systems

455

()

−=+

⎡

⎤

+= −

⎢

⎥

⎣

⎦

sin cos sin ,

cos sin sin ,

λψλ ψ θψϕθ

λψλψ ψθ ϕθ

 







so that we can eliminate Lagrange’s multipliers. Thus, the relation (22.2.59') leads to

+=sin 0θψϕ θ

 



(22.2.62)

while the relation (22.2.59'') leads to the relation

()

⎡⎤

+=−

⎢⎥

⎣⎦

2d d

cos sin sin

5d dtt

ϕψ θ ψθ ϕ θ θ





which can be written in the form

()

⎡⎤

+=−

⎢⎥

⎣⎦

2d d

cos sin sin

5d d

ϕψ θ ψ ϕ θ θ

θθ



too, after simplifying by

≠ 0θ



. Replacing

ϕ

given by (22.2.60) and effecting the

computations, we get

d3cos 2

dsin2 sin2

Aψθ

θθ θ



wherefrom, by integration, it results

sin cos , constAC Cψθ θ=+ =



(22.2.63)

We have thus obtained three first integrals (22.2.60), (22.2.61) and (22.2.63),

sufficient to determine the angular velocities

,ψθ



and ϕ ; the integration constants

,,ABC

are determined by imposing initial conditions for these velocities.

Eliminating



and

ϕ

between (22.2.60), (22.2.61) and (22.2.63), it results

()

=−

cos

sin



(22.2.64)

wherefrom, by a quadrature, we obtain

= ()tθθ ; the equations (22.2.63) and (2.2.60)

lead then, successively, to

= ()tψψ and = ()tϕϕ , by two other quadratures.

Replacing



and ϕ in (22.2.62), one observes easily that (22.2.64) is a first integral

of this differential equation.

Let us assume now that the horizontal plane is rotating with a constant angular

velocity

Ω about the

′′

Ox -axis. In this case, the constraint relations (22.2.58) are

completed in the form

MECHANICAL SYSTEMS, CLASSICAL MODELS

456

()

′′

−− +=

′′

++ −=

sin sin cos 0,

cos sin sin 0;

xR x

θψϕθψΩ









(22.2.65)

hence, the mechanical system remains non-holonomic and scleronomic, with three

degrees of freedom.

Besides the generalized co-ordinates

1234

,,,,qqqqq introduced above, we denote

too; the quasi-co-ordinates

, 1,2,...,6

iπ =

, will be specified by the

differential relations

()

′′

=− + − −

′′

=+ + −

′

==+

′

== +

′

== −

11 2

22 1

d d sin d sin cos d d ,

dd cosdsinsind d,

dddcosd,

ddcosdsinsind,

d d sin d sin cos d ,

dd,

xR xt

πψθθψϕΩ

πω ψ θϕ

πω ψθ θψϕ

(22.2.66)

while the corresponding virtual variations will be given by

()

′

δ=−δ+ δ− δ

′

δ=δ+ δ+ δ

δ=δ+ δ

δ= δ+ δ

δ= δ− δ

δ=

sin sin cos ,

cos sin sin ,

cos ,

cos sin sin ,

sin sin cos ,

πψθθψϕ

πψ θϕ

πψθθψϕ

(22.2.67)

Solving the systems (22.2.66) and (22.2.67) with respect to the real and virtual

generalized displacements, respectively, we obtain

′′

=− + −

′′

=− +

=−

11 26

22 416

ddd d,

dd d d,

d d sin cot d cos cot d ,

dcosd sind,

d sin cosec d cos cosec d ,

dd,

xRx

ππΩπ

ψπ ψθπ ψθπ

θψπ ψπ

ϕψθπ ψθπ

(22.2.66')

as well as

Dynamics of Non-holonomic Mechanical Systems

457

′

δ=−δ+δ

′

δ=δ−δ

δ=δ − δ + δ

δ= δ + δ

δ= δ − δ

δ=

22 4

sin cot cos cot ,

cos sin ,

sin cosec cos cosec ,

ππ

ψπ ψθπ ψθπ

θψπ ψπ

ϕψθπ ψθπ

(22.2.67')

The relations (22.2.17) lead to the matrices

[]

′

−−−

⎡⎤

⎢⎥

′

−

⎢⎥

−

⎢⎥

⎣⎦

100 sin sincos

010 cos sinsin

001 0 cos 0

000 cos sinsin 0

000 sin sincos 0

000 0 0 1

RR x

ψθψΩ

ψθψ

[]

′

−−

⎡⎤

⎢⎥

′

−−

⎢⎥

−

⎢⎥

−

⎢⎥

⎣⎦

100 0

010 0

001 sincot coscot 0

000 cos sin 0

0 0 0 sin cosec cos cosec 0

000 0 0 1

Ω

ψθ ψθ

ψψ

ψθ ψθ

;

the formulae (22.1.23) allow to calculate

=− = =− =− =− =

=− =− =− = =− =−

=− = =− =− =− =

11 11 11

34 43 26 62 46 64

22 22 22

35 53 16 61 56 65

33 44 55

45 54 35 53 34 43

,,,

,, ,

1, 1, 1.

γγ γγΩγγΩ

γγ γγΩγγ Ω

γγ γγ γγ

The transposition relations (22.1.24') are given by

()()

δ−δ = δ− δ − δ−δ

δ−δ =− δ− δ + δ−δ

δ−δ = δ− δ

δ−δ =

11 3443 642

55 5

22 3 3 6 1

334 4

44 33

34 43

dd d d d ,

ddd d,

dd0.

ππ ππππΩπππ

ππππππ

ππ

(22.2.68)

MECHANICAL SYSTEMS, CLASSICAL MODELS

458

Lagrange’s equations in quasi-co-ordinates (22.2.22) become (we have

0, 1,2,...,6

Qj== )

⎛⎞

∂∂ ∂

−− =

⎜⎟

∂∂ ∂

⎝⎠

⎛⎞

∂∂ ∂

−+ =

⎜⎟

∂∂ ∂

⎝⎠

⎛⎞ ⎛ ⎞

∂∂ ∂ ∂ ∂ ∂

−− − + − =

⎜⎟ ⎜ ⎟

∂∂ ∂ ∂ ∂ ∂

⎝⎠ ⎝ ⎠

** *

11 2

** *

22 1

** * * * *

33 1 2 4

TT T

TT T T T T

Ω

ππ π

Ω

ππ π

ππ ππ

ππ π π π π



 



(22.2.69)

()

⎛⎞

∂∂ ∂ ∂ ∂

−+ −− + =

⎜⎟

∂∂ ∂ ∂ ∂

⎝⎠

⎛⎞

∂∂ ∂ ∂ ∂

−+ −+ + =

⎜⎟

∂∂ ∂ ∂ ∂

⎝⎠

⎛⎞ ⎛ ⎞

∂∂ ∂ ∂

−+ − =

⎜⎟ ⎜ ⎟

∂∂ ∂ ∂

⎝⎠ ⎝ ⎠

** * * *

44 1 3

** * * *

343

234

** * *

66 1 2

TT T T T

TT T T

πΩ π π

ππ π π π

πΩ π π

ππ π π π

Ωπ π

ππ π π













(22.2.69')

where we noticed that

0ππ

(the constraint relations (22.2.65)) and

1π

Taking into account (22.2.65), (22.2.66), we can express the kinetic energy in the form

()()

()

* 22 2 2

5 5

126241634

TM R x R x iππΩπ ππΩπ πππ

′′

⎡

=−++−++++

⎤

⎦

⎣

      

(22.2.58')

where we have introduced the gyration radius

i given by =

/iIM.

We can calculate

()

∂∂

′′

=− − = + −

⎡

⎤

⎣

⎦

∂∂

241

MR x M R i RxπΩ π Ω

ππ



()

∂∂

′′

=− − = + −

⎡

⎤

⎣

⎦

∂∂

41 2

MR x M R i RxπΩ π Ω

ππ



()

∂∂

′′ ′ ′

==+−+

⎡

⎤

⎣

⎦

∂∂

222

312141

Mi M x x R x xπΩΩ ππ

ππ





as well, taking into account (22.2.19), we get

() ()

∂∂

′′

=+ = −

∂∂

MR x MR R xπΩ ΩπΩ

ππ

,

() ()

∂∂

′′

=− − =− −

∂∂

41 41

MR x MR R xπΩ ΩπΩ

ππ

,

()

∂∂

′′

== −

∂∂

24 1

MR x xΩπ π

ππ

.

Dynamics of Non-holonomic Mechanical Systems

459

The third equation (22.2.69) leads to

0π , hence to

′

constπω ,

(22.2.70)

and the fourth and the fifth equation of this system lead to (

41 2

, πωπω

′′′

==)

()

′′′

+− −=

′′′

++ −=

122

211

Ri RR x

ωΩωΩ



(22.2.70')

where we took into account the constraint relations (22.2.65); using, further, these

relations and integrate them, we obtain

() ()

′′

+−= +

′′

+−= +

22 22

111

22 22

222

Ri RxCRi

ωΩ

(22.2.71)

C and

C being arbitrary constants. The same relations (22.2.65) allow to eliminate

the components of the rotation vector, so that

′′

−=

122

211

xxCR

Ω



(22.2.72)

with the notation

222

[/( )]iRiΩΩ; there result the equations

()

′′

+= = −

′′

−= = +

1133 21

2244 12

xxCCRCC

ΩΩ



(22.2.72')

the integration constants being determined by initial conditions.

Hence, in general, the centre of the sphere which moves on a rough horizontal plane,

which is rotating with a constant angular velocity about a fixed axis, describes an

ellipse, the parameters of which depend on the initial conditions and which is fixed with

respect to the inertial frame of reference.

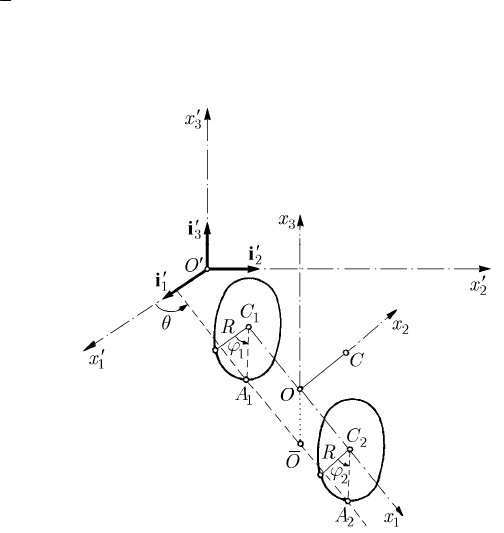
22.2.3.4 Motion of the Two-Wheeled Carriage

Let us consider a Roman carriage, formed by a rigid solid S of mass M ,

supported at the points

A and

A on a horizontal plane

′′′

Oxx by two equal wheels,

of radii

R and masses m , which are independently rotating with the velocities

ϕ and

ϕ , about the centres

C and

C , respectively; the movable frame of reference has the

pole at the middle of the distance between the two centres (

2CC a), the

Ox -axis

being along the line of the centres, which makes the angle

θ with the

′′

Ox -axis, the

Ox -axis being horizontal, while the

Ox -axis is vertical and parallel to the

′′

Ox -axis.

The mass centre

of the car is on the

-axis, so that =OC l (Fig. 22.14).

MECHANICAL SYSTEMS, CLASSICAL MODELS

460

Let

O be the projection of the pole O on the plane

′′′

Oxx of co-ordinates

′′

,xx;

in this case, the variables

′′

=====

11223 4 1 2

,,,,qxqxq q qθϕ ϕ can form a

system of generalized co-ordinates.

Fig. 22.14 Motion of a two-wheeled carriage

Assuming that the wheels are rolling and pivoting without sliding on the fixed plane,

we impose the condition that the velocities of the points of both wheels, which – at the

considered moment – coincide with the points of contact

A and

A , respectively, do

vanish. Thus, for the point

A we can write

′′ ′

=+× =+× +× =

vv v

22 2

21 2 22

CC O C

CA OC CA 0

JJJJG JJJJJG

JJJG

ωωω,

where

()

′′′′′ ′ ′ ′

=+ = + =−

′′′

== +

vii i i i

iii

11 22 2 1 2 2 2 3

3212

,cossin, ,

,cossin,

xxOCa CARθθ

θϕθθ

JJJJG

JJJG





ωω

′

i ,1,2,3

k , being the unit vectors of the axes of the fixed frame of reference.

Projecting on the axes of this frame, we obtain (the projection on the

′′

Ox -axis is

identically equal to zero)

() ()

12 22

sin 0, cos 0xaR xaRθϕ θ θϕ θ

′′

−+ = ++ =



 

(22.2.73)

Analogously, equating to zero the absolute velocity of the point

A , it results

Dynamics of Non-holonomic Mechanical Systems

461

() ()

11 21

sin 0, cos 0xaR xaRθϕ θ θϕ θ

′′

+− = −− =



 .

(22.2.73')

These four constraint relations are not independent (the rank of the matrix of the

unknowns

′′

12 1

,,,xxθϕ



 

and

ϕ is not four). From the relations (22.2.73) and (22.2.73')

one obtains the relations

′′

−=−+=+

12 1 2

sin cosx x aR aRθ θ θϕ θϕ



  ,

(22.2.74)

wherefrom results the holonomic constraint

()

+−=

20aRθϕϕ



 ;

(22.2.74')

indeed, by integration we have

()

+−=

22aR akθϕϕ ,

(22.2.75)

so that one can determine the non-dimensional constant

k if the initial values of the

three angles are given.

As well, from each system of relations (22.2.73) and (22.2.73'), respectively, one

obtains the differential consequence

cos sin 0xxθθ

′′

+= ;

(22.2.76)

one can thus see that the velocity

′

has no component along the axle of the carriage

(the

Ox -axis), hence being normal to this one, which was to be expected, because the

axle cannot slide along itself (the velocities of the points

A and

A vanish at any

moment and the bar

CC is rigid). From the relations (22.2.74) we get also the

constraint relation

()

′′

−=+

12 12

sin cos

xx Rθθϕϕ 

(22.2.76')

One can show that the system (22.2.76), (22.2.76') does not admit any integrable

combinations, so that the two-wheeled carriage is a non-holonomic system with two

degrees of freedom.

If we denote by

′

T the kinetic energy of the carriage (the axle and the mechanical

system which lies on it) with respect to the fixed frame or reference, we can write

()

′′′

=++

2222

TMxxiθ





(22.2.77)

where

i is the gyration radius of the system with respect to the

Ox -axis, in the

hypothesis in which its mass centre is at the point

O . In the case in which the mass

centre is at the point

C (

sin , cos , xl xl Rθθ

′′

−+), one must use the velocity of