Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

432

We must have

′

v , because the point O is moving along the axis

Ox ; it results

the constraint force

()

′

RMvωωρ



(22.2.3)

Taking into account (22.2.2) and denoting

Mρ

(22.2.4)

we can write the equations of motion in the form

′′

=+=

vvk

ωρ ρ



;

eliminating the velocity

′

v , we get



Multiplying by

/ωω



and integrating, it results the differential equation of first order

(

)

2222

kkC



(22.2.5)

where

C is an integration constant.

By a change of variable

⎡

⎤

=∈−

⎣

⎦

cos , ,

ππ

ωψψ

(22.2.5')

it results

222

cosCψψ



; we choose the sign of the constant C in (22.2.5) so as to

have

= cosCψψ



. Hence, we can write

−

∫

d11sin

cos 2 1 sin

αψ

and then

−

−−

−

== ==

sin tanh , cos

cosh

Ct Ct

Ct Ct Ct Ct

ee ee

ψψ

;

it results that

∈−∞∞[,]t , because ∈−[/2,/2]ψππ, the change of variable (22.2.5')

covering the whole interval of time. Finally, we obtain

= kωψ



, wherefrom – by

integration and by a convenient determination of the integration constant – we get

= kϕψ;

hence, the sleigh is rotating by the angle

kπ for a variation of the time t from −∞ to ∞ .

Finally,

Dynamics of Non-holonomic Mechanical Systems

433

()

= arcsin tanhkCtϕ .

(22.2.6)

Starting from

′

=− = =

22 2

11 1

tan sin

vk k Ck

ρρψψ ρψ



and from

′′ ′′

11 21

cos , sin

OO OO

xv xvϕϕ

and observing that

dd/cos, /tC kψψψϕ==, we can write the equations of motion

of the point

O with respect to the fixed frame in the form

′′

∫

tan cos d ,

tan sin d .

xxk k

ρψψψ

(22.2.7)

We can determine thus the trajectory of the point

O in the plane Π for various values

of the parameter

k ; but we notice that for =

0ρ (the projection of the mass centre C on

the plane

Π coincides with the contact point O of the knife with this plane) we have

=∞k , so that the equation of motion can no more be written in the form (22.2.5). The

equations (22.2.1'), (22.2.2) lead to

= constω ,

′

const

v ; hence, the point O has a

uniform motion in a direction which is rotating with a constant angular velocity, describing

thus a circle of radius

′

rvω .

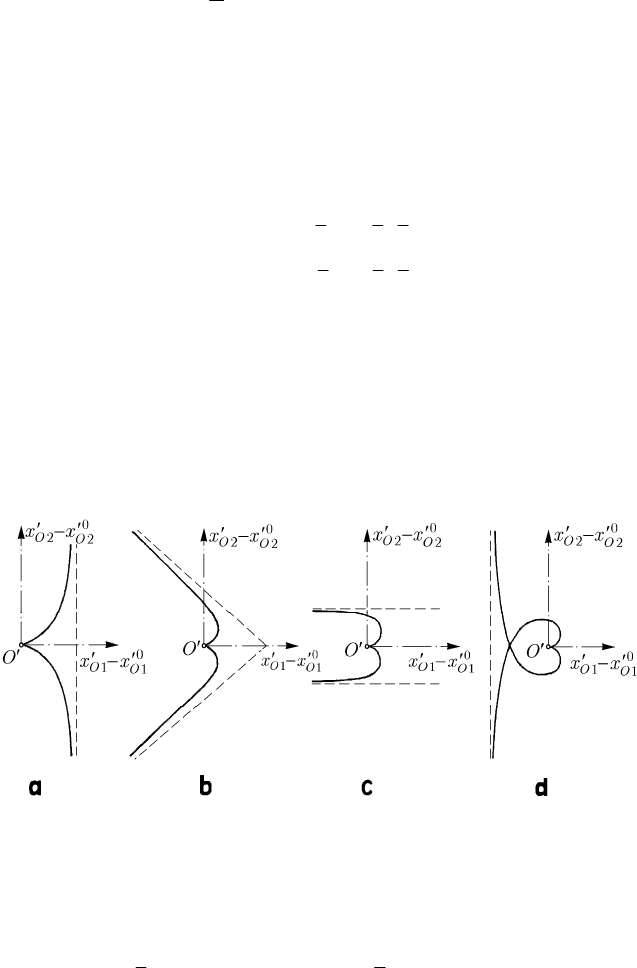
Fig. 22.11 Trajectories of the contact point of the knife edge in the motion

of a rigid solid on a horizontal plane

≠

0ρ , then the trajectory (22.2.7) has only a single point for = 0ψ ; to determine

the nature of the singularity, we consider expansions of the form

′′ ′′

−= + −= +

022 0 33

11 22

..., ...

OO OO

xx k xx kρψ ρψ ,

(22.2.7')

MECHANICAL SYSTEMS, CLASSICAL MODELS

434

which put in evidence the cuspidal point for

= 0ψ . The straight line

′′

xx is a

symmetry axis of this curve; observing that

d/d tan

xx kψ

′′

= and that

(

)

→

−=<∞

∫

lim tan sin d

ψπ

ρψψψα

we can state that

′′

tan

xx k

is an asymptote of the considered trajectory. The trajectories of the point

O for = 1k ,

= 3/2k , = 2k and = 3k are represented in Fig 22.11a–d, respectively; the point O

stops at the cuspidal point, at which the velocity vanishes.

22.2.1.2 Motion of a Sphere on a Rough Fixed Surface

Let us consider a homogeneous sphere S of mass M , acted upon by forces the

resultant of which passes through the centre

O ; we assume that the sphere rolls on a

perfect rough surface

Σ . We use a movable frame of reference R of co-ordinate axes

123

Ox x x , so that

Ox passes through the contact point P between the sphere and the

surface

Σ . Let Ω and

be the instantaneous angular velocities of the movable frame

and of the sphere, respectively, v

(,,0)vv be the velocity of the point O with respect

to a fixed frame and

F and R

(,,)TT N be the resultants of the given forces, applied

O , and of the constraint forces, applied at P , respectively (Fig. 22.12). The

components of these quantities are taken along the axes of the frame of reference

R .

Fig. 22.12 Motion of a sphere on a rough fixed surface

The equations of motion read

()

−=+

132 11

231 22

12 21 3

Mv v F T

Mv v FN

Ω

ΩΩ



(22.2.8)

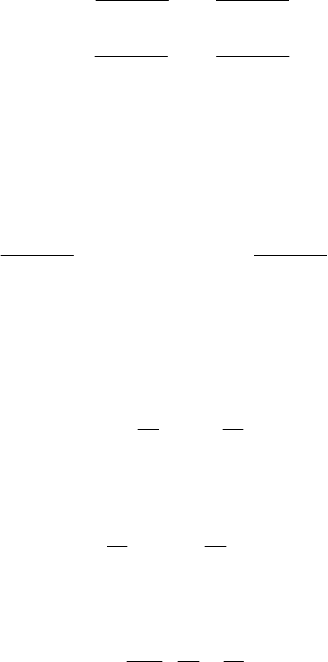
Dynamics of Non-holonomic Mechanical Systems

435

()

−+ =

−+ =−

−+=

13223 2

21331 1

32112

ITr

ωΩωΩω



(22.2.8')

where

is the moment of inertia of the sphere with respect to a diameter of it; the

conditions of rolling without sliding are given by

12 21

0, 0vr vrωω−= +=.

(22.2.9)

Eliminating the constraint forces

T and

T and the angular velocities

ω and

ω , it

results

−= +

+= +

132 1 13

231 2 23

vv F r

IMr IMr

vv F r

IMr IMr

ΩΩω



(22.2.10)

These equations put in evidence the motion of the centre

O of the sphere, the trajectory

of which is on the surface

′

, formed by the extremities of the normals, of length r ,

to the surface

Σ ; the point O is acted upon by the given forces, reduced in the ratio

/( )Mr I Mr , and by the forces

⎡⎤⎡⎤

+−

⎢⎥⎢⎥

⎣⎦⎣⎦

13 32 23 31

MrvMrv

IMr IMr

Ωω Ω Ωω Ω ,

respectively. We choose the axes

Ox and

Ox along the lines of curvature of the

surface

′

, of radii of curvature of the normal sections to the surface

ρ and

ρ ,

respectively; in this case

ΩΩ

ρρ

(22.2.11)

Meusnier’s theorem (4.1.19) leads to

312

tan tan

Ωθθ

ρρ

(22.2.11')

Taking into account the third equation (22.2.8'), it results

⎛⎞

=−

⎜⎟

⎝⎠

ρρ



(22.2.11'')

Let

′′′

123

OOO

xxx be the co-ordinates of the point O ; the velocities

v and

v can

be obtained, in this case, starting from the equation of the surface, as functions of

MECHANICAL SYSTEMS, CLASSICAL MODELS

436

′′′

123

OOO

xxx, by decomposing the velocity along the axes of the frame of reference

R . Eliminating the quantities

12 1 2

,, ,vvΩΩ and

Ω by means of the relations

(22.2.10), (22.2.11), and (22.2.11'), we obtain three equations for the unknowns

123

,,ΩΩΩ and

ω and their derivatives with respect to time; together with the

equation of the surface

′

, we have thus at our disposal a system of four equations,

sufficient to specify the motion of the sphere.

Obviously, in various particular cases one obtains important simplifications of

calculation. For instance, in case of the rolling of a sphere on a plane we have

0ΩΩ

and, assuming that the frame of reference R is chosen so that

0Ω

it results

1122

vFvF

IMr IMr



(22.2.12)

Thus, the motion of the mass centre of the sphere does not depend on the component

of the angular velocity

, which is constant. As a matter of fact, this problem has

been considered in Sect. 17.1.2.7 too. Other interesting particular cases are these in

which the surface

is a sphere, a cylinder or a cone or – more general – a surface of

rotation.

22.2.2 Lagrange’s Equations

In what follows, we take again the equations with multipliers of Lagrange; as well,

we establish Lagrange’s equations in quasi-co-ordinates.

22.2.2.1 Lagrange’s Equations with Multipliers

In the frame of Lagrangian mechanics, one can make a systematic study of the

motion of a non-holonomic mechanical system by means of Lagrange’s equations with

multipliers (see Sect. 18.2.2.2)

∂∂

⎛⎞

−=+ =

⎜⎟

∂∂

⎝⎠

∑

,1,2,...,

kkj

Qaj s

tq q



(22.2.13)

where the last sums correspond to the components

=, 1,2,...,

Rj s, of the constraint

generalized force, a study in this direction being made by Ed. Routh. To determine the

+sm unknowns (the functions ( ), 1,2,...,

qqtj s==, and the parameters

λ ,

= 1,2,...,km), we use the s Lagrange’s equations with multipliers and the <ms

non-holonomic constraint relations (18.2.9'), which can be – conveniently – written in the

form

, 1,2,...,

kj k

aq a k m=− = .

(22.2.14)

Applying the methodology in Sect. 18.2.3.4 to the equations (22.2.13), one obtains

the relation

Dynamics of Non-holonomic Mechanical Systems

437

()

−= + −

jj jj

TT Qq RqT





(22.2.15)

analogue to the relation (18.2.60'). We notice that

==−

∑∑

jj j

kkj kk

Rq a q aλλ ,

(22.2.16)

where we took into account (22.2.14). Hence, in case of catastatic constraints

(

a ,

= 1,2,...,ks

) we have = 0

Rq , so that the relation (22.2.15) is reduced

to the relation (18.2.60'). We can thus state that, in case of non-holonomic and catastatic

constraints, one obtains a first integral of Painlevé of the form (18.2.61), in the same

conditions in which this is obtained in case of holonomic (in general, non-catastatic)

constraints.

As well, in case of a non-holonomic and catastatic mechanical system, for which the

generalized forces are quasi-conservative, assuming a simple quasi-potential in the form

(18.2.20), we can introduce the kinetic potential (18.2.34), obtaining the relation

(18.2.62); if the kinetic potential

L does not depend explicitly on time ( = 0



), we

find again Jacobi’s first integral (18.2.63). Obviously, in the condition of some

catastatic constraints (and only in such a condition) one can obtain all types of first

integrals mentioned in Sect. 18.2.3.4 (e.g., a first integral of Jacobi type).

But we must notice that this method of calculation is not completely satisfactory.

Indeed, because the generalized co-ordinates are not independent, one must take into

account the

m constraint relations (22.2.14). But these relations contain generalized

velocities, so that we cannot express

m dependent generalized co-ordinates as

functions of

−nm independent generalized co-ordinates ; one cannot thus eliminate

these co-ordinates between the respective relations and the equations (22.2.13). To

realize this and to remove Lagrange’s multipliers from the equations of motion, one can

introduce quasi-co-ordinates instead of generalized co-ordinates.

22.2.2.2 Lagrange’s Equations in Quasi-co-ordinates

We have introduced in Sect. 22.1.2.2 the quasi-co-ordinates by the relations

(22.1.17) or (22.1.18) or by the relations (22.1.18') or (22.1.18''), for which one can

write the relations of transposition (22.1.24). As one can see, the quasi-co-ordinates

allow a generalization of Lagrange’s equations, by unifying their form in case of

non-holonomic systems. To put in evidence the importance of this generalization, from

the practical as well as from the formal point of view, it is sufficient to mention that the

choice of convenient unknown parameters (generalized co-ordinates and

quasi-co-ordinates which determine the motion) plays a very important rôle in the study

of some particular mechanical problems. We mention thus the problem of motion of the

rigid solid with a fixed point, which has been formulated and studied by Euler in

quasi-co-ordinates, although he did not use this motion. One can mention also other

researches where the velocities of the points of a mechanical system in motion have

been put in evidence (e.g., the non-holonomic problem of rolling of a

non-homogeneous sphere on a plane, considered by Chaplygin), using the

quasi-co-ordinates. But only at the beginning of last century the generalized

co-ordinates and the kinematic characteristics have lead to a unified concept, that of

MECHANICAL SYSTEMS, CLASSICAL MODELS

438

quasi-co-ordinates. In 1904, G. Hamel has deduced Lagrange’s equations in

quasi-co-ordinates (which he called Lagrange–Euler equations), applicable to

holonomic as well as to non-holonomic mechanical systems.

Let be a mechanical system

S definite by the generalized co-ordinates

q and by

the quasi-co-ordinates

, 1,2,...,

jsπ = , linked by the relations (22.1.18) or (22.1.18'),

where we make

α , hence

0, , 1,2,...,

ik sβ == (catastatic case) too; we

can write

, , , , , 1,2,...,

iijjj ij

jk k jk ik

qq ijk sπα βπαβ== =δ=  ,

(22.2.17)

where

12 12

( , ,..., ), ( , ,..., ), , , 1,2,...,

ij ij

jk jk

qq q qq q ijk sαα β β== =. Observing

that the relation

=∂ ∂ =d(/)d d

iijjijj

qq qππ α

leads to

∂∂=/

ij ij

qπα

and that

analogously we have

∂∂=/

kjk

q πβ, we obtain

∂∂

== == =

∂∂ ∂∂

, , , , 1,2,...,

ijk s

ππ

αβ

ππ





(22.2.18)

Thus, for any function

( , ,..., ; )

ffqq qt or =

(,,...,;)

ggqq qt  , the relations

∂

∂∂ ∂∂ ∂

== = =

∂∂∂∂∂∂

, , 1,2,...,

jk jk

jj j

kk k

ff fg g

qq q

ββ

ππ π

(22.2.19)

take place; as well, for any function

( , ,..., ; )

ff tππ π or =

( , ,..., ; )

gg tππ π 

we have

∂∂∂∂

===

∂∂∂∂

, , 1,2,...,

ij ij

jjjj

ffgf

αα

ππ

(22.2.19')

Taking into account (22.1.22'), we can write the relation (18.2.27'), corresponding to

the application of the principle of the virtual work (which led us to Lagrange’s

equations (18.2.29) for holonomic constraints), in the form

∂∂

⎡⎛ ⎞ ⎤

−− δ=

⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎦

jk k

tq q

βπ



;

because the variations

π of the quasi-co-ordinates are arbitrary, it results

∂∂

⎡⎛ ⎞ ⎤

−− ==

⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎦

0, 1,2,...,

Qks

tq q



(22.2.20)

If we denote by

T the function which is obtained by replacing in T the

generalized velocities

q by the quasi-velocities

π , we have

Dynamics of Non-holonomic Mechanical Systems

439

12 12 12

12 1 2 12 1 2

( , ,..., ; , ,..., ) ( , ,..., ; , ,..., )

( , ,..., ; , ,..., ) ( , ,..., ; , ,..., ).

ss s

kk kk skk

ss s

jjsjj

Tqq qqq q Tqq q

Tqq q Tqq q q q q

βπβπ βπ

ππ π α α α

    

Starting from here and using the relations (22.2.17), (22.2.18), (22.2.18’), and

(22.2.19'), we can write

∂

⎛⎞∂∂∂ ∂∂

⎛⎞ ⎛ ⎞

=−=+

⎜⎟

⎜⎟ ⎜ ⎟

∂∂∂∂∂∂∂

⎝⎠ ⎝ ⎠

⎝⎠

∂∂

⎛⎞

∂∂∂ ∂∂

=+ =+

⎜⎟

∂∂∂∂∂∂∂

⎝⎠

** **

dd d

;

jk ij

jk jk jk ml l

jjji i

im im

jk jk jk ml l

j j ij ij

TTT TT

tq t q qq t q

TTT TT

qqq q

ββ ββπ

ππ

αα

ββ ββπ

πππ



 



replacing in (22.2.20), it results

∂

⎛⎞∂∂ ∂

⎛⎞

−+ − =

⎜⎟

∂∂ ∂∂∂

⎝⎠

** *

kml l jk

TT T

tqq

ββ π β

ππ π





Introducing the generalized forces

,1,2,...,

kjk

QQ k sβ

(22.2.21)

corresponding to the virtual variations

π , and using the notations (22.1.23), we get

the equations

⎛⎞∂∂ ∂

−+ =

⎜⎟

∂∂ ∂

⎝⎠

** *

TT T

γπ

ππ π





which we rewrite in the form

⎛⎞

∂∂ ∂

−+ = =

⎜⎟

∂∂ ∂

⎝⎠

** *

, 1,2,...,

jj i

TT T

Qj s

γπ

ππ π





;

(22.2.22)

by analogy with Lagrange’s equations (18.2.29), we have thus obtained Lagrange’s

equations in quasi-co-ordinates, in catastatic, hence scleronomic case (Hamel’s

equations).

One can show that, in the general non-holonomic and rheonomous case, the

equations (22.2.22) are completed in the form

⎛⎞

∂∂ ∂ ∂

−+ + =+ =

⎜⎟

∂∂ ∂ ∂

⎝⎠

** * *

,1,2,..,

kj k k

jj i i

TT T T

QRj s

γπγ

ππ π π





(22.2.22')

where, starting from the constraint generalized forces

R (see Sect. 22.2.2.1), we

introduce also the generalized forces

, 1,2,...,

kjk

RR k sβ ,

(22.2.21')

MECHANICAL SYSTEMS, CLASSICAL MODELS

440

the coefficients

γ being given by (22.2.23); these are the Boltzmann–Hamel equations.

As well, the quantities

∂

, 1,2,...,

pjs



(22.2.23)

are the quasi-momenta corresponding to the quasi-co-ordinates. If a virtual variation

12 1 1

... 0, 0, ... 0

πππππ π

−+

δ=δ==δ = δ≠ δ ==δ= corresponds to a

rotation about an instantaneous axis of rotation, then the generalized forces

Q and the

quasi-momenta

p are, as usual, the moment of the force and the moment of

momentum, respectively, with respect to the axis.

, ,...,

ππ π are generalized co-ordinates (true co-ordinates), then the relations of

momentum (22.2.17) are integrable, so that the coefficients

vanish, while the

equations (22.2.22) become the equations (18.2.29) of Lagrange.

The expression (18.2.15), (18.2.15'), (18.2.15'') and (18.2.15''') of the kinetic energy

allows to write

T in the form (in holonomic and catastatic, hence scleronomic case)

ij i j

Tgππ

(22.2.24)

where we have introduced the notations

ij ji

kl ki lj

gg gββ ,

(22.2.25)

by means of the relations (22.2.17). We calculate thus

∂∂=

ij i

Tgππ, and then

∂

⎛⎞∂

⎜⎟

∂∂

⎝⎠

∂

∂∂

;

kk kl

πππ

ππ







observing that the product

ππ is symmetric with respect to the indices k and l , it

results

⎛⎞

∂∂∂

⎜⎟

∂∂∂

⎝⎠

***

jk jk jl

kl kl

llk

ggg

ππ ππ

πππ

 

so that we can write the equations (22.2.22) in the form (we introduce the generalized

forces

R , corresponding to a scleronomic and non-holonomic mechanical system)

[]

()

++ =+=

****

, , 1,2,...,

jk k kj li k l

gkljg QRj sπγππ   ,

(22.2.26)

Dynamics of Non-holonomic Mechanical Systems

441

where we have introduced Christoffel’s symbols of first kind

[]

⎛⎞

∂∂

∂

=+− =

⎜⎟

∂∂∂

⎝⎠

, , , , 1,2,...,

jk jl

kl j j k l s

πππ

(22.2.27)

We have thus obtained a system of

s linear equations in the quasi-velocities

, 1,2,...,

ksπ = .

Let

kkj

gg be the algebraic complement of the element

g in the determinant

⎡

⎤

⎣

⎦

det

; the normalized algebraic complement will be ==

****

jk kj jk

gggg.

We notice that the relations

⎡⎤

==δ

⎣⎦

***

det ,

kmjm

ggg

(22.2.28)

where

is Kronecker’s symbol, take place. Multiplying the system of equations

(22.2.26) by

*mj

g and summing with respect to j , it results (we replace then the free

index

m by

)

⎛⎧ ⎫ ⎞

⎪⎪

++ =+=

⎜⎟

⎨⎬

⎜⎟

⎪⎪

⎝⎩ ⎭ ⎠

, 1,2,...,

jjj

QRj s

πγππ

   ,

(22.2.29)

where we have introduced Christoffel’s symbols of second kind, definite by

[]

⎧⎫

⎪⎪

⎨⎬

⎪⎪

⎩⎭

, , , , 1,2,...,

kl m g j k l s

(22.2.27')

as well as the notations

, , , 1,2,...,

mi mj

kl kj li

gg mkl sγγ ,

(22.2.30)

===

******

, , 1,2,...,

mj mj

QQgRRgm s.

(22.2.30')

The system of equations (22.2.29) represents thus the normal form of Hamel’s

equations, in which the quasi-accelerations are expressed as functions of

quasi-velocities and quasi-co-ordinates; this form of the equations (analogue to the form

(18.2.47') of Lagrange’s equations) can be always obtained, because

≠

0g .

In case of a non-holonomic mechanical system with

<ms catastatic constraints of

the form

−+

0, 2,...,

smkj

aqk m ,

(22.2.31)

hence with

−sm degrees of freedom, it is often convenient to use quasi-co-ordinates,

so that

m quasi-co-ordinates (in case of the notations used above, these