Teodorescu P.P. Mechanical Systems, Volume III: Analytical Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

412

22.1.1.1 Preliminary Notions

In the study of non-holonomic mechanical system we use, as till now, a discrete

modelling, their state being specified – at a given moment – by a finite number of

parameters. We will consider further systems formed by particles and rigid solids.

It is necessary to use the notions of real displacement

rd , possible displacement Δr

and virtual displacement δr introduced in Sect. 3.2.1.1 for the space

E , in Sects. 18.1.1.2

and 18. 2.1.2 for the spaces

E , and

, respectively. Let be a mechanical systems S of

particles

, of position vectors r

, subjected to constraints expressed, in general, by real

displacements

, = 1,2,...,in, in the form (3.2.13), if the constraints are bilateral, or in

the form (3.2.14), if these ones are unilateral; excepting special cases, we will consider only

bilateral constraints. The constraint relations are expressed in the form (3.2.15), using

virtual displacements δr

. If the differential forms of first degree by which these relations

are expressed are (locally) non-integrable, hence if there do not exist integrant factors for

the corresponding equations, then the respective constraints are non-holonomic (kinematic)

constraints.

Passing to the space

Λ , the constraint relations expressed by means of the generalized

displacements

=d , 1,2,...,

qj s, are of the form (see Sect. 18.2.1.2 too)

+==

( ; )d ( ; )d 0, 1,2,...,

kj k

aqtq a qtt k m,

(22.1.1)

or of the form

+==

( ; ) ( ; ) 0, 1,2,...,

kj k

aqtq a qt k m ,

(22.1.1')

where

{

}

≡

, ,...,

qqq q are generalized co-ordinates. If =

a , then the con-

straints are catastatic (and homogeneous) and if we have also

0, 1,2,...,

ak m== , = 1,2,...,

s , then these constraints are even scleronomic. As

well, the constraints expressed by means of these relations are non-holonomic

(anholonomic) if there does not exist an integrant factor for the corresponding differential

equations. In Sect. 3.2.2.6, Frobenius’s theorem, which specifies the necessary and

sufficient conditions of holonomy for a constraint system, is given. Using the virtual

generalized displacements

q , the constraint relations read

δ= =( ; ) 0, 1,2,...,

aqtq k m.

(22.1.2)

The existence of non-holonomic constraints has not been known by Lagrange, nor by other

researchers; only in 1894, H. Hertz made distinction between holonomic and

non-holonomic constraints.

A simple example (the motion of a rigid skate on the ice plane) has been given in Sect.

3.2.2.6. Let be now a circular disc, of centre

O and radius R , which is rolling on the plane

Π (not necessarily horizontal), where we situate the system of axes

′′′

Oxx ; its position is

specified by the co-ordinates

′

x and

′

x of the contact point I , by the angle

between

the tangent to the disc at

I and the

′′

Ox -axis, by the inclination angle θ of the plane of

Dynamics of Non-holonomic Mechanical Systems

413

the disc with respect to the plane

and by the angle ϕ , which gives the position of a

point

of the contour with respect to the point

(Fig. 22.1, where the sense of the

angles is put into evidence). The infinitesimal displacement of the disc is characterized by

the real displacements

d,d,d,dxxψθ and dϕ . In case of a rolling without sliding of the

disc on the plane

Π , case in which the relative velocity of the contact point I vanishes,

one can easily see that (the projections of the arc

dR ϕ

on the two axes of co-ordinates)

d cos d 0, d sin d 0xR xRϕϕ ϕϕ

′′

+=+=

(22.1.3)

cos , sinxR xRϕψ ϕψ

′′

=− =−.

(22.1.3')

We mention that the five generalized co-ordinates can take any value among the set of

possible values, hence that the disc can have any position with respect to the plane.

Indeed, starting from an initial position

′′

00000

,,,,xxψθϕ

, one can reach any other

position

′′

11111

,,,,xxψθϕ. Firstly, the disc rolls from the contact point

()

′′

000

,Ixx till

the contact point

()

′′

111

,Ixx

, along a curve of length

()

2, Rkkϕϕ π−+ ∈`

then it rotates about the normal at

I to the plane Π , till =

ψψ, and – finally – it

inclines till

θθ

. Hence, the conditions (22.1.3) or (22.1.3') do not impose any

restrictions to the values which can be taken by the considered generalized

co-ordinates; these constraints are non-holonomic and scleronomic.

Fig. 22.1 Rolling of a circular disc on a plane

In the case of a system of differential forms of first degree, it is not sufficient that

only one form be non-integrable so that the corresponding mechanical system be

non-holonomic. Let be, e.g., the differential forms

() ()

=+ + = =+ + =

22 22

1121133 2122233

dd0, dd0xxxxxx xxxxxxωω ;

MECHANICAL SYSTEMS, CLASSICAL MODELS

414

each of these forms, taken apart, is non-integrable, but combinations of them lead to

()( )()

+++=+ =

123

22 222 22

12 12

d0,dln0

xx xxx xx

;

The number

r of kinematic degrees of freedom of a mechanical system is equal to

the number of linear independent virtual displacements of this system. In case of a

holonomic mechanical system, this number equates the number of the generalized

co-ordinates (

=rs), while in case of a non-holonomic one we have =−rsm. Let

be the circular disc which rolls without sliding on a horizontal plane, considered above

(Fig. 22.1); the constraint relations are written in the form

′′

δ + δ= δ + δ=

cos 0, sin 0xR xRψϕ ψϕ .

(22.1.3'')

These equations admit three independent systems of solutions, i.e.:

(i)

′′

δ=− δδ=− δδδ=δ=

cos , sin , , 0xR xRψϕ ψϕ ϕ θ ψ ,

(ii)

′′

δ =δ = δ=δ= δ

0, 0,xx ψϕ θ,

(iii)

′′

δ=δ=δ=δ=δ

0, 0,xx ϕθ ψ,

corresponding to the virtual rotations of the disc about an axis normal to the disc at the

point

I , about the tangent to the disc at the contact point, as well as about an axis

normal to the plane

Π at the point I , respectively.

22.1.1.2 Representative Spaces

We have introduced the space of configurations

Λ in Sect. 18.2.1 the representative

point

P being specified by a minimal parameterization =, 1,2,...,

qj s. In a

qualitative dynamical theory, the topological structure of this space plays an important

rôle; in this order of ideas, we consider some particular cases.

Fig. 22.2 Frictionless sliding of a ball S along the axis of a rigid pendulum

Let be a physical pendulum for which the axis of suspension passes through

O and

the position of which with respect to a vertical axis is specified by the angle

θ ; we

consider a rectilinear guide rail along the pendulum (the

Ox -axis) on which slides

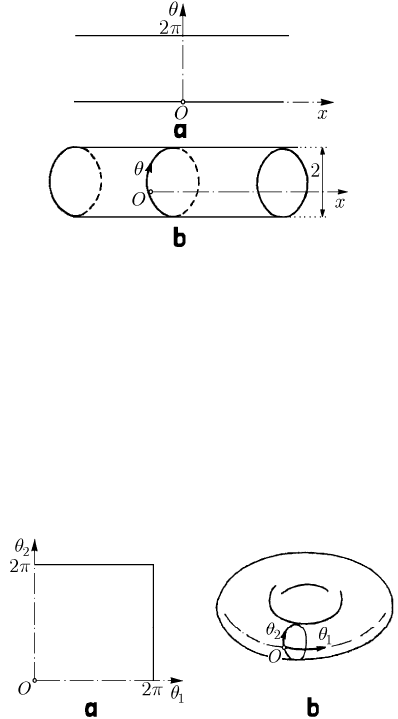
Dynamics of Non-holonomic Mechanical Systems

415

frictionless a small body (a ball)

S , its position being thus given by the generalized

co-ordinates

x and θ (Fig. 22.2). The correspondence between the point P in the

plane of configurations (

,x θ

) and the configuration of the mechanical system is not

one-to-one, because to two points (

,x θ ) and ( +,2xkθπ), ∈k ] , corresponds only

one position of the considered mechanical system; to have a one-to-one

correspondence, we must limit ourselves to the strip

≤<02θπ

(Fig. 22.3a). But we

Fig. 22.3 Physical pendulum; plane (a strip) (a) and cylindrical (b) space of configurations

notice that to two close configurations of the mechanical system

S , i.e. (

,x ε

) and

(

,2 , 0x πεε−>, arbitrary small), correspond two points of the strip, which are

distant one of the other; hence, to a continuous motion of the system

S does not

correspond a continuous displacement of the representative point. To restore the

continuity, we roll the strip on a circular cylinder of radius equal to unity and “glue” the

opposite sides. The cylinder can be thus considered to be the space of configurations

corresponding to the mechanical system

S , the correspondence between the positions

of the mechanical system and the points of the cylinder being one-to-one and

continuous (Fig. 22.3b).

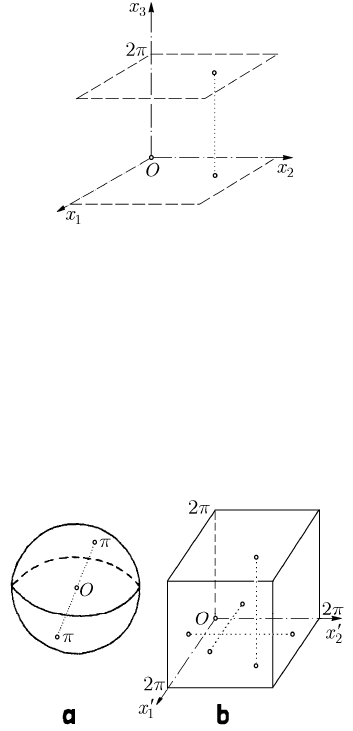
Fig. 22.4 Double pendulum; plane (a square) (a) and a three-dimensional (torus) (b)

space of configurations

In case of a double pendulum, the position of which is specified by the angles

and

(see Sect. 17.1.1.2, Fig.17.1a), the one-to-one correspondence is ensured if one takes

as space of configurations a square of side

≤<

2(0 , 2)πθθπ (Fig. 22.4a). If one

rolls the square on a cylinder, gluing the opposite sides

0θ

and

2θπ

, and then

one bends the cylinder, gluing the opposite faces

0θ

and

2θπ

, one obtains a

MECHANICAL SYSTEMS, CLASSICAL MODELS

416

torus (Fig. 22.4b); this is the space of configurations in case of the double pendulum,

the continuity being – as well – ensured.

Fig. 22.5 Rigid skate – three-dimensional space of configurations

In Sect. 3.2.2.6 we have considered the motion of a rigid skate

AB on the ice plane

(plane

Ox x , Fig. 3.16). The position of the segment AB is specified by the

co-ordinates

x and

x of the middle C of this segment and by the angle θ made by it

with the

Ox -axis; one has the constraint relation (3.2.31) between these generalized

co-ordinates. The space of configurations is three-dimensional and is formed by the

stratum

≤<02θπ, two opposite points of the planes = 0θ and = 2θπ being

considered to be united (Fig. 22.5); one cannot obtain a “gluing together” in the

three-dimensional space.

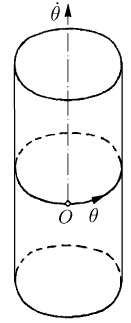
Fig. 22.6 Spaces of configurations: rigid solid with a fixed point (a); circular disc

rolling without sliding on a horizontal plane (b)

One can be show that to a rigid solid with a fixed point corresponds as space of

configurations the interior (with the frontier) of a sphere of radius π ; the diametrical

opposite points on the sphere must be considered united (Fig. 22.6a). As well, in case of

a circular disc constraint to roll slidingless on a horizontal plane (Fig. 22.1), the space

of configurations is formed from the interior (with the frontier) of a cube of side equal

2π , two opposite points (of opposite faces) of which being united (Fig. 22.6b),

together with the plane of the contact points (

′′

,xx); one obtain thus a pentadimen-

sional space of configurations (the space of configurations is the same if the motion

takes place with sliding).

Dynamics of Non-holonomic Mechanical Systems

417

The state of a mechanical system

S is specified by the generalized co-ordinates

and by generalized velocities

, 1,2,...,

qj s= . If there exist m relations of non-holo-

nomic constraints of the form (22.1.1) or (22.1.1'), then it is sufficient to use

−sm

generalized velocities, determining the other generalized velocities starting from these

relations; instead of generalized velocities one can use kinematic characteristics of the

form

=+ = −

, 1,2,...,

iijji

qi smωα α ,

(22.1.4)

i.e. linear combinations of generalized velocities with

( , ,..., ; )

ij ij

qq qtαα ,

= 1,2,...,js, where

[

]

≠det 0

(22.1.4')

and

( , ,..., ; )

qq qtαα . The mechanical system S is thus specified by

−2sm co-ordinates, i.e. s generalized co-ordinates and −sm kinematic

characteristics, which form the phase space

−2sm

Γ .

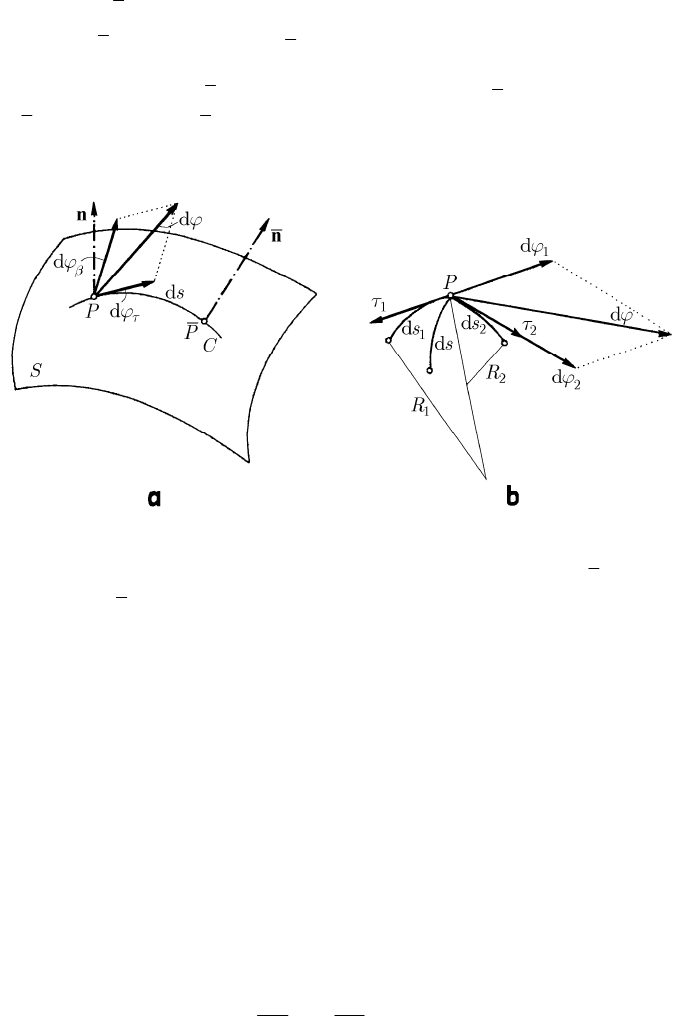
Fig. 22.7 Space phase of a physical pendulum

For instance, the state of a physical pendulum is specified by an angle

θ and by a

generalized angular velocity



; the corresponding phase space is a circular cylinder, θ

being along the director circle, while



is along the generatrix, the correspondence

with the state of the physical pendulum being one-to-one and continuous (Fig. 22.7).

In the problem of the rigid skate on the ice plane (known as Chaplygin’s problem)

can be introduced the kinematic characteristic

cos sinvx xθθ instead of

x

and

x , hence the velocity of the middle C of the segment AB ; the co-ordinates

,,,xxθ ,v θ



lead thus to a pentadimensional phase space. This space cannot be

MECHANICAL SYSTEMS, CLASSICAL MODELS

418

visualized, but one can visualize sections in this space, e.g.

constx and

= constθ



22.1.1.3 Kinematics of the Rolling of a Rigid Solid on Another One

Let be two rigid solids

S and

′

S , bounded by two convex surfaces S and

′

respectively, which – at any moment

t have the same tangent plane at an ordinary

common point

, , PPPSP S

′′′

≡∈∈ (see Sect. 5.3.3.1, Fig. 5.29); to fix the ideas,

we admit that the rigid solid

′

is fixed, while the rigid solid S is movable,

remaining permanently in contact with the rigid solid

′

. The velocity v ()

t of a

movable point

Q which coincides with

′

≡PP

at any moment

is the velocity of

transportation (velocity of sliding) with respect to the fixed surface

′′

=−vvv()

QPP

, contained in the common tangent plane. If =v

0 , then the

surface

S rolls without sliding over the surface

′

. The motion of the rigid solid S

with respect to the rigid solid

′

S is specified if the angular velocity vector ()tω ,

which passes through the point

is given too; hence, this motion is characterized by a

translation of velocity

v ()

and by a rotation of angular velocity ()tω .

The vector

()tω can be decomposed in two components: an angular velocity ()

tω

along the normal to the tangent plane, which characterizes a pivoting about the

respective axis, and an angular velocity

()

tω , contained in the tangent plane, which

characterizes a rolling about the corresponding axis. In general, the motion of the rigid

solid

S over the rigid solid

′

S takes place so that the surface S is rolling and

pivoting with sliding on the surface

′

. If =v ()

t 0 , then the motion of the rigid solid

S with respect to the rigid solid

′

S is an instantaneous rotation (pivoting and rolling)

about an instantaneous axis of rotation which passes through the point of contact. The

fixed axoid

intersects the surface

′

along the curve

′

(the locus of the point Q

with respect to the surface

′

), while the movable axoid

A intersects the surface S

along the curve

C (the locus of the point Q with respect to the surface S ); in this case

′

=vv

, so that – during the motion – the curve C rolls without sliding over the

curve

′

. In particular, if ==0( )

ωωω, then the surface S is rolling slidingless

over the surface

′

(pure rolling; e.g., the rolling of a cylinder, when the instantaneous

axis of rotation is the contact generatrix); analogously, if

()

==0ωωω, then the

surface

S is pivoting without sliding over the surface

′

(pure pivoting, e.g., the

rotation of a sphere on a horizontal plane about its vertical diameter). If

≠v ()

t 0 ,

then the particular rotations considered above are associated with a sliding.

To can establish the constraint relations which take place in the considered motion,

one must determine the connection between the angle of rotation

=ddtθω and the

arcs

ds and

′

, described by the contact point

on the curve C and on the curve

′

, respectively. Introducing the angle of rotation d

θ , corresponding to the pure

rolling, and the angle of rotation

θ , corresponding to the pure pivoting, we may

write

=+dd d

θθ θ

;

(22.1.5)

Dynamics of Non-holonomic Mechanical Systems

419

we notice that the arc elements

ds and

′

depend only on d

θ , because the point

does not move during the pivoting.

Let

and P be two successive contact points on the surface

, along the curve

C , so that

= dPP s , while n and =+nn nd are unit vectors normal to S at these

points, respectively (Fig. 22.8a); analogically, corresponding to the surface

′

, we

consider the points

′

and the unit vectors

′

n and

′′ ′

n=n n+d . Because

××nn=n nd and

′′ ′ ′ ′

××≅×

nn=n n n ndd, we can write

()

′′

=× +× =× +

nnnnn n nddd dd

θ .

(22.1.6)

Fig. 22.8 Geometric elements at two successive points (a) or at a point (b) of a surface

Let us denote by d

and

′

the angles made by the normals n and n and by the

normals

′

n and

′

n , respectively; we can write (we notice that ⋅=nnd0)

=× = ×

′′ ′′ ′′

=× = ×

nnn n

dd,dd,

dd,dd.

ϕϕ

(22.1.7)

We decompose

along the tangent to the curve C and along the normal to it

(

=+dd d

ϕϕ ϕ

; Fig. 22.8a); the vector d

is contained in the tangent plane (as

well as the vector

). The angle d

is the angle of curvature, while the angle

is the angle of torsion. If the curve C is a line of curvature of the surface S , then

the torsion vanishes and the angle of curvature is given by

=dd/sR

, where R is

the corresponding principal radius of curvature. Let

τ and

τ be the unit vectors

tangent to the lines of curvature at

P ,

ds and

ds the elements of arc along these

lines and

and

the corresponding radii of curvature (Fig. 22.8b); we can thus

write

=− +

ττ.

(22.1.8)

MECHANICAL SYSTEMS, CLASSICAL MODELS

420

Observing that

′

=+ddd

ϕϕ

, it results

′′

=− + − +

′′

2121

1212

2121

dddd

ssss

RRRR

ττττ,

(22.1.9)

where we use analogous notations for the surface

′

. Let be

dτ

and

′

τ the

projections on the common tangent plane of the variations of the unit vectors tangent to

the curves

C and

′

at the point Q , respectively; we notice that

′

=−ddd

θττ.

The velocity of pivoting is thus given by

()

′

==−

KKv

, (22.1.10)

where

= d/d

vst, while = d/d

Ksτ and

′

= d/d

Ksτ

are the geodesic

curvatures of the curves

and

′

, respectively, at the same point Q .

Fig. 22.9 Rolling of a sphere on a horizontal plane

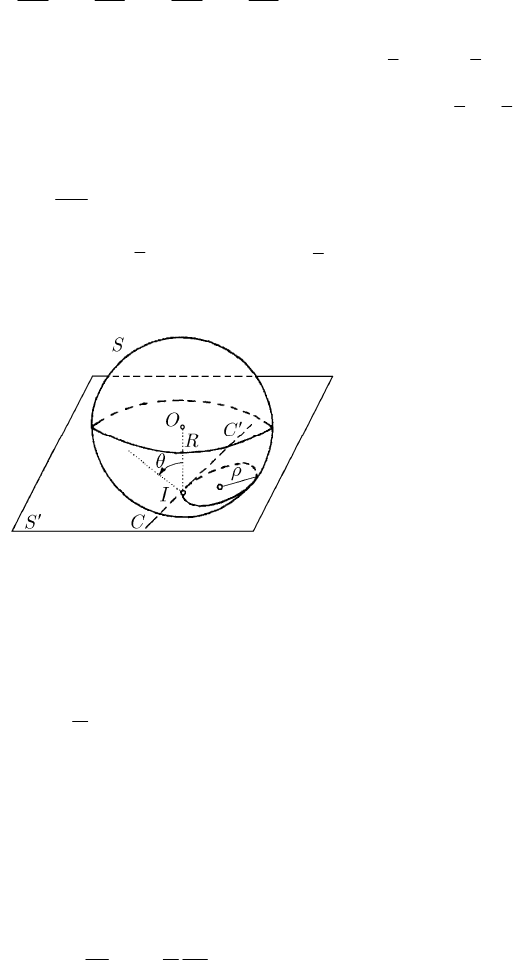
In particular, let us consider the rolling of a sphere of radius

R on a horizontal plane

with a constant angular velocity

; the principal radii of curvature of the sphere being

equal to

R , while those of the plane being infinite, it results

()

=−

21 12

ddd

θττ,

(22.1.11)

wherefrom the angular velocity of the pure rolling is given by

= d/d

tωθ.

The velocity of displacement of the contact point is normal to the angular velocity

ω and has the magnitude =

vRω . The curve

′

in the fixed plane is a straight

line, while the curve

C on the sphere is a circle of constant geodesic curvature given

(22.1.12)

Dynamics of Non-holonomic Mechanical Systems

421

To calculate this curvature, we notice that

1/ /cos , sin

KRρθρ θ==, where ρ is

the radius of the circle

C , while the angle θ specifies the inclination of the plane (Fig.

22.9). Eliminating the angle

, we get

=−

Rρ

(22.1.12')

In connection with the motion of a rigid solid which slides frictionless on a fixed

plane, we mention the considerations in Sect. 17.1.2.3. In particular, one considers

the case of a heavy homogeneous rigid solid of rotation (in Sect. 17.1.2.4), the case

of a heavy gyroscope (in Sect. 17.1.2.5), the case of a rigid cylindrical solid (in

Sect. 17.1.2.6) and the case of a sphere (in Sect. 17.1.2.7), the fixed plane being

horizontal. The motion without sliding of a sphere on a fixed plane is studied in

Sect. 17.1.2.7 too; in Sect. 17.1.2.8 has been considered the case of a hollow

homogeneous sphere, the plane being horizontal. As well, the motion without

sliding of a heavy circular disc has been presented in Sect. 17.1.2.9.

22.1.2 Conditions of Holonomy. Quasi-co-ordinates. Non-holonomic

Spaces

In what follow, we will present firstly some conditions of holonomy, we introduce

then the notion of quasi-co-ordinate, the corresponding relations of transposition being

also established. As well, we make considerations concerning the introduction of the

non-holonomic spaces too.

22.1.2.1 Conditions of Holonomy

Let be a mechanical system S , the representative point (;)qt of which is

subjected, in general, to the constraint relations (22.1.1), written in the form (

tq,

for the uniformity of the notation)

()

∑

; d 0, 1,2,...,

aqtq k m.

(22.1.13)

From the geometric point of view, these conditions show that a point in the space

(;)qt

cannot be displaced arbitrarily, but only along a curve which is tangent at any point of it

to a

−()sm-dimensional hyperplane, which contains all the vectors

d,d,d,qqq

...,d

, which satisfy the conditions (22.1.13); if the system (22.1.13) is not integrable,

then the representative point can occupy any point in the space

(;)qt , although the

imposed restrictions.

First of all, let us consider the particular case

= 3s , with a scleronomic constraint

relation

()() ()

++=

1 123 1 2 123 2 3 123 3

,, d ,, d ,, d 0a qqq q a qqq q a qqq q ;

(22.1.14)